2.6一元一次不等式组第2课时 课件(共24张PPT)
文档属性
| 名称 | 2.6一元一次不等式组第2课时 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 885.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 12:15:06 | ||
图片预览






文档简介
(共24张PPT)
北师大版 数学 八年级下册
第2课时
第二章 一元一次不等式与一元一次不等式组
6 一元一次不等式组
学习目标
1.解较复杂的一元一次不等式组;(重点、难点)
2.一元一次不等式组的实际应用.(难点)
复习回顾
1.一般地,关于 未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
2.一元一次不等式组中各个不等式的解集的 ,叫做这个一元一次不等式组的解集.
3.一元一次不等式组的解法:
①标注序号,②分别求解,③在数轴上找出公共部分,④写出不等式组的解集.
4.一元一次不等式组解的情况:
.
同一个
公共部分
同大取大,同小取小,大小小大中间找,大大小小无处找
一、创设情境,引入新知
问题:在什么条件下,长度为3cm , 7cm ,x cm的三条线段可以围成一个三角形 你和同伴所列的不等式组一样吗?解集呢?与同伴交流.
所以,x的取值范围为4解不等式①得:
解不等式②得:
你和同伴所列的不等式组不一定相同,但解集一定相同.
解:利用三角形三边关系可知:
三角形任意两边之和大于第三边,三角形任意两边之差小于第三边
在同一条数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
探究一:解较复杂的一元一次不等式组
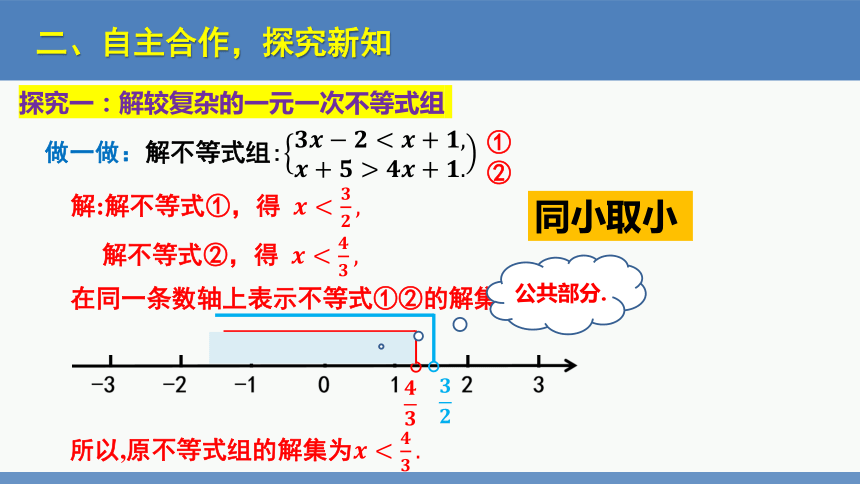
解:解不等式①,得
解不等式②,得
做一做:解不等式组:
①
②
所以,原不等式组的解集为
公共部分.
同小取小
在同一条数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
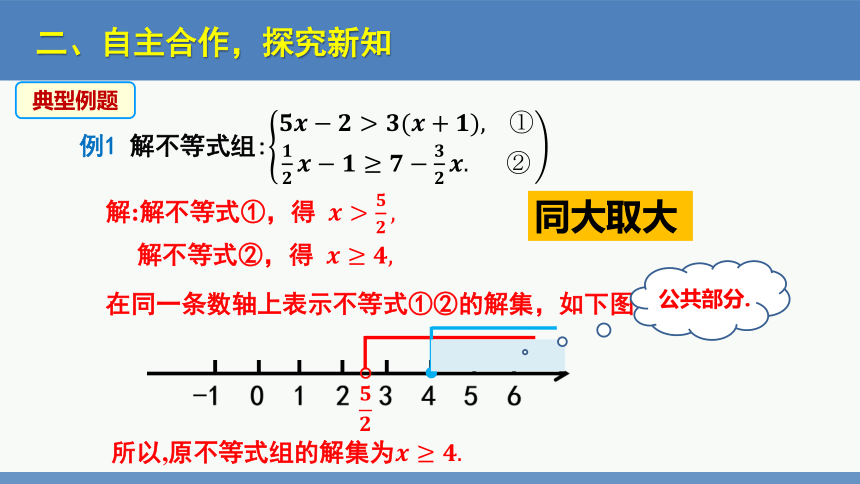
解:解不等式①,得
解不等式②,得
所以,原不等式组的解集为
典型例题
公共部分.
例1 解不等式组:
同大取大
二、自主合作,探究新知
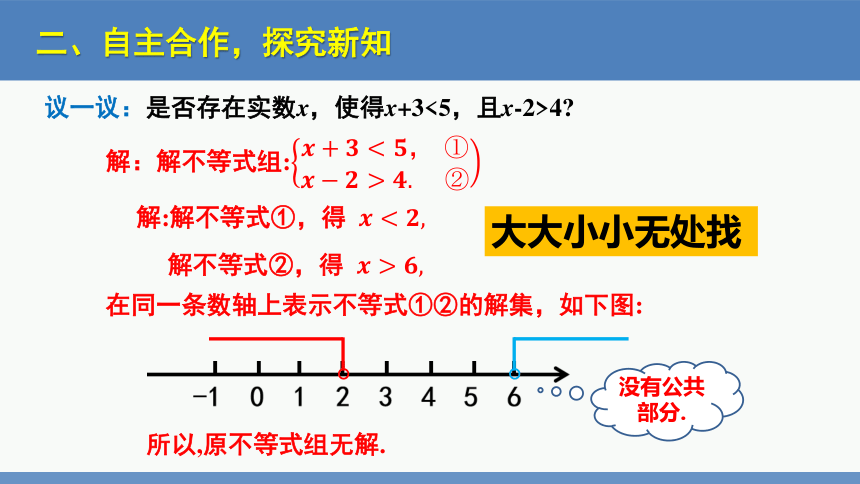
议一议:是否存在实数x,使得x+3<5,且x-2>4
在同一条数轴上表示不等式①②的解集,如下图:
解:解不等式①,得
解不等式②,得
所以,原不等式组无解.
解:解不等式组:
没有公共部分.
大大小小无处找
二、自主合作,探究新知
知识要点
注意:(1)不等式中有分母、有括号的要先去分母、去括号,分别计算出两个不等式的解集后分别表示在数轴上,由公共部分确定不等式组的解集.
(2)解一元一次不等式组及在数轴上表示一元一次不等式组的解集时,要注意实心圆点与空心圆圈的区别.
二、自主合作,探究新知
典型例题
因为不等式组的解集为: -1< x < 1 ,
所以 (a+1)(b-1)=2×(-3)=-6.
解: 由不等式组得:
所以,
解得
例2:已知不等式组的解集为-1<x<1, 则(a+1)(b-1)的值为多少
二、自主合作,探究新知
探究二:一元一次不等式组的应用
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
做一做:用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.
解不等式组,得5<x <7.
依题意得
知识要点
二、自主合作,探究新知
利用一元一次不等式解决实际问题时,首先列出准确的一元一次不等式组是关键,其次未知数的取值要符合实际意义.
二、自主合作,探究新知
例3:某地区发生严重旱情,急需饮水设备12台.现有甲、乙两种设备可供选择,其中甲种设备的购买费用为4 000元/台,安装及运输费用为600元/台;乙种设备的购买费用为3 000元/台,安装及运输费用为800元/台.若要求购买的费用不超过40 000元,安装及运输费用不超过9 200元,则可购买甲、乙两种设备各多少台?
典型例题
解:设购买甲种设备x台,则购买乙种设备(12-x)台.
根据题意,得
解得 2≤x≤4.
因为x为整数,所以x=2,3,4.
故有三种购买方案:(方案一)购买甲种设备2台,乙种设备10台;(方案二)购买甲种设备3台,乙种设备9台;(方案三)购买甲种设备4台,乙种设备8台.
2.“a与5的和是正数且a的一半不大于3”用不等式组表示,正确的是( )
1.不等式组的解集为( )A.无解 B.x≤1 C.x≥-1 D.-1≤x≤1
三、即学即练,应用知识
D
A
4.如图,有长为40 m的篱笆,现利用一面墙围成中间隔有一道篱笆的矩形花圃ABCD,墙的长度MN=30 m,要使靠墙的一边AD的长不小于25 m,设与墙垂直的一边AB的长为x m,可得不等式组: .
3.某中学学生乘汽车从学校去研学旅行基地,以75 km/h的平均速度,用时2 h到达.由于天气原因,原路返回时汽车的平均速度控制在不低于50 km/h且不高于60 km/h的范围内,这样需要用t h到达,则t的取值范围为 .
三、即学即练,应用知识
2.5≤t≤3
三、即学即练,应用知识
解: (1)解不等式①,得x≤2.
解不等式②,得x>1.所以不等式组的解集为1解: (2)解不等式①,得x≥4.解不等式②,得x>1.所以不等式组的解集为x≥4.将解集表示在数轴上如图所示:
5.解不等式组,并把解集在数轴上表示出来.
(1) (2)
三、即学即练,应用知识
6.求不等式组3<≤7的整数解.
解: (1)原不等式组可化为解不等式①,得x>;
解不等式②,得x≤所以此不等式组的解集为四、课堂小结
利用公共部分确定不等式组的解集
分步解不等式
去分母、去括号
一元一次不等式组2
解较复杂的一元一次不等式组
实际应用
首先列出准确的一元一次不等式组是关键,其次未知数的取值要符合实际意义.
2.若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )A.m>4 B.m≥4 C.m<4 D.m≤4
1.对于不等式组下列说法正确的是( )A.此不等式组的正整数解为1,2,3B.此不等式组的解集为-1五、当堂达标检测
A
D
4.若关于x的不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
五、当堂达标检测
a≤-6
3.一群女生住若干间宿舍,每间住4人,剩19人无房住;若每间住6人,则有一间宿舍不满也不空,问可能有多少间宿舍?若设可能有x间宿舍,可列不等式组: .
五、当堂达标检测
解: 解不等式①,得x<3.
解不等式②,得x≥1.所以不等式组的解集是1≤x<3.
将解集表示在数轴上如图所示:
5.解不等式组,并把解集在数轴上表示出来.
五、当堂达标检测
解: 解不等式①得,x≥-3,
解不等式②得,x<2,所以不等式组的解集是-3≤x<2,
所以它的整数解为-3,-2,-1,0,1,所有整数解的和为-3-2-1+0+1=-5.
6.解不等式组并求出它的所有整数解的和.
五、当堂达标检测
7.某单位举办活动,计划购买甲、乙两种纪念品共100件进行发放,其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各多少件;
解: (1)设购买甲种纪念品x件,则购买乙种纪念品(100-x)件.根据题意,得120x+80(100-x)=9600,解得x=40,则100-x=60.故购买甲种纪念品40件,购买乙种纪念品60件.
五、当堂达标检测
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过购买甲种纪念品件数的2倍,并且总费用不超过9400元,那么购买甲、乙两种纪念品共有几种方案 请一一列明,并指出哪一种方案所需总费用最少,最少总费用是多少元.
(2)购买甲种纪念品m件,则购买乙种奖品(100-m)件.根据题意,得解得≤m≤35.因为m为整数,所以m=34或m=35.当m=34时,100-m=66,总费用为34×120+66×80=9360(元);当m=35时,100-m=65,总费用为35×120+65×80=9400(元).故活动主办方共有2种购买方案,方案一:购买甲种纪念品34件,购买乙种纪念品66件;方案二:购买甲种纪念品35件,购买乙种纪念品65件.方案一所需总费用最少,最少总费用为9360元.
教材习题2.9.
六、布置作业
北师大版 数学 八年级下册
第2课时
第二章 一元一次不等式与一元一次不等式组
6 一元一次不等式组
学习目标
1.解较复杂的一元一次不等式组;(重点、难点)
2.一元一次不等式组的实际应用.(难点)
复习回顾
1.一般地,关于 未知数的几个一元一次不等式合在一起, 就组成一个一元一次不等式组.
2.一元一次不等式组中各个不等式的解集的 ,叫做这个一元一次不等式组的解集.
3.一元一次不等式组的解法:
①标注序号,②分别求解,③在数轴上找出公共部分,④写出不等式组的解集.
4.一元一次不等式组解的情况:
.
同一个
公共部分
同大取大,同小取小,大小小大中间找,大大小小无处找
一、创设情境,引入新知
问题:在什么条件下,长度为3cm , 7cm ,x cm的三条线段可以围成一个三角形 你和同伴所列的不等式组一样吗?解集呢?与同伴交流.
所以,x的取值范围为4
解不等式②得:
你和同伴所列的不等式组不一定相同,但解集一定相同.
解:利用三角形三边关系可知:
三角形任意两边之和大于第三边,三角形任意两边之差小于第三边
在同一条数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
探究一:解较复杂的一元一次不等式组
解:解不等式①,得
解不等式②,得
做一做:解不等式组:
①
②
所以,原不等式组的解集为
公共部分.
同小取小
在同一条数轴上表示不等式①②的解集,如下图:
二、自主合作,探究新知
解:解不等式①,得
解不等式②,得
所以,原不等式组的解集为
典型例题
公共部分.
例1 解不等式组:
同大取大
二、自主合作,探究新知
议一议:是否存在实数x,使得x+3<5,且x-2>4
在同一条数轴上表示不等式①②的解集,如下图:
解:解不等式①,得
解不等式②,得
所以,原不等式组无解.
解:解不等式组:
没有公共部分.
大大小小无处找
二、自主合作,探究新知
知识要点
注意:(1)不等式中有分母、有括号的要先去分母、去括号,分别计算出两个不等式的解集后分别表示在数轴上,由公共部分确定不等式组的解集.
(2)解一元一次不等式组及在数轴上表示一元一次不等式组的解集时,要注意实心圆点与空心圆圈的区别.
二、自主合作,探究新知
典型例题
因为不等式组的解集为: -1< x < 1 ,
所以 (a+1)(b-1)=2×(-3)=-6.
解: 由不等式组得:
所以,
解得
例2:已知不等式组的解集为-1<x<1, 则(a+1)(b-1)的值为多少
二、自主合作,探究新知
探究二:一元一次不等式组的应用
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
做一做:用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.
解不等式组,得5<x <7.
依题意得
知识要点
二、自主合作,探究新知
利用一元一次不等式解决实际问题时,首先列出准确的一元一次不等式组是关键,其次未知数的取值要符合实际意义.
二、自主合作,探究新知
例3:某地区发生严重旱情,急需饮水设备12台.现有甲、乙两种设备可供选择,其中甲种设备的购买费用为4 000元/台,安装及运输费用为600元/台;乙种设备的购买费用为3 000元/台,安装及运输费用为800元/台.若要求购买的费用不超过40 000元,安装及运输费用不超过9 200元,则可购买甲、乙两种设备各多少台?
典型例题
解:设购买甲种设备x台,则购买乙种设备(12-x)台.
根据题意,得
解得 2≤x≤4.
因为x为整数,所以x=2,3,4.
故有三种购买方案:(方案一)购买甲种设备2台,乙种设备10台;(方案二)购买甲种设备3台,乙种设备9台;(方案三)购买甲种设备4台,乙种设备8台.
2.“a与5的和是正数且a的一半不大于3”用不等式组表示,正确的是( )
1.不等式组的解集为( )A.无解 B.x≤1 C.x≥-1 D.-1≤x≤1
三、即学即练,应用知识
D
A
4.如图,有长为40 m的篱笆,现利用一面墙围成中间隔有一道篱笆的矩形花圃ABCD,墙的长度MN=30 m,要使靠墙的一边AD的长不小于25 m,设与墙垂直的一边AB的长为x m,可得不等式组: .
3.某中学学生乘汽车从学校去研学旅行基地,以75 km/h的平均速度,用时2 h到达.由于天气原因,原路返回时汽车的平均速度控制在不低于50 km/h且不高于60 km/h的范围内,这样需要用t h到达,则t的取值范围为 .
三、即学即练,应用知识
2.5≤t≤3
三、即学即练,应用知识
解: (1)解不等式①,得x≤2.
解不等式②,得x>1.所以不等式组的解集为1
5.解不等式组,并把解集在数轴上表示出来.
(1) (2)
三、即学即练,应用知识
6.求不等式组3<≤7的整数解.
解: (1)原不等式组可化为解不等式①,得x>;
解不等式②,得x≤所以此不等式组的解集为
利用公共部分确定不等式组的解集
分步解不等式
去分母、去括号
一元一次不等式组2
解较复杂的一元一次不等式组
实际应用
首先列出准确的一元一次不等式组是关键,其次未知数的取值要符合实际意义.
2.若关于x的一元一次不等式组的解集是x>3,则m的取值范围是( )A.m>4 B.m≥4 C.m<4 D.m≤4
1.对于不等式组下列说法正确的是( )A.此不等式组的正整数解为1,2,3B.此不等式组的解集为-1
A
D
4.若关于x的不等式组的解集中的任意x,都能使不等式x-5>0成立,则a的取值范围是 .
五、当堂达标检测
a≤-6
3.一群女生住若干间宿舍,每间住4人,剩19人无房住;若每间住6人,则有一间宿舍不满也不空,问可能有多少间宿舍?若设可能有x间宿舍,可列不等式组: .
五、当堂达标检测
解: 解不等式①,得x<3.
解不等式②,得x≥1.所以不等式组的解集是1≤x<3.
将解集表示在数轴上如图所示:
5.解不等式组,并把解集在数轴上表示出来.
五、当堂达标检测
解: 解不等式①得,x≥-3,
解不等式②得,x<2,所以不等式组的解集是-3≤x<2,
所以它的整数解为-3,-2,-1,0,1,所有整数解的和为-3-2-1+0+1=-5.
6.解不等式组并求出它的所有整数解的和.
五、当堂达标检测
7.某单位举办活动,计划购买甲、乙两种纪念品共100件进行发放,其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各多少件;
解: (1)设购买甲种纪念品x件,则购买乙种纪念品(100-x)件.根据题意,得120x+80(100-x)=9600,解得x=40,则100-x=60.故购买甲种纪念品40件,购买乙种纪念品60件.
五、当堂达标检测
(2)设购买甲种纪念品m件,如果购买乙种纪念品的件数不超过购买甲种纪念品件数的2倍,并且总费用不超过9400元,那么购买甲、乙两种纪念品共有几种方案 请一一列明,并指出哪一种方案所需总费用最少,最少总费用是多少元.
(2)购买甲种纪念品m件,则购买乙种奖品(100-m)件.根据题意,得解得≤m≤35.因为m为整数,所以m=34或m=35.当m=34时,100-m=66,总费用为34×120+66×80=9360(元);当m=35时,100-m=65,总费用为35×120+65×80=9400(元).故活动主办方共有2种购买方案,方案一:购买甲种纪念品34件,购买乙种纪念品66件;方案二:购买甲种纪念品35件,购买乙种纪念品65件.方案一所需总费用最少,最少总费用为9360元.
教材习题2.9.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
