17.4 反比例函数(第1课时)课件(共30张PPT)-八年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 17.4 反比例函数(第1课时)课件(共30张PPT)-八年级数学下册同步精品课堂(华东师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 18:42:23 | ||
图片预览











文档简介
17.4 反比例函数
第1课时 反比例函数
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、理解并掌握反比例函数的概念;
2、从实际问题中抽象出反比例函数的模型,能根据已知
条件确定反比例函数的解析式;
温故知新
1.函数的概念:
在一个变化过程中有( ),如果对于x的每一个值,y都有
( )的值与它对应,那么就说y是x的函数, x是( ).
2.反比例关系:
两个变量x和y
唯一
自变量
两个变量的( )是一个( )的常数,则称这两个变量成反比例.
积
不为零
新课导入
?
?
新学期伊始,小明想买一些笔记本为以后的学习做准备. 妈妈给了小明 30 元钱,小明可以如何选择笔记本的价钱和数量呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}笔记本单价x/元
1.5
2
2.5
3
5
7.5
…
购买的笔记本数量y/本
…
通过填表,你发现 x,y 之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
讲授新课
知识点一 反比例函数的概念
解:
V和t的积为2,V和t成反比例
1.小明同学家离学校 2km.小明每天骑自行车上学, 问:他骑车的速度V
(km/h)和他骑车所需的时间t(h)有怎样的数量关系?(列算式)
∵速度=路程÷时间
讲授新课
2.北京到杭州铁路线长为1161 km.一列从北京开往杭州火车,全程行驶时间为x(h),行驶平均速度为:y(km/h).
(1)完成下表;
(2)在表格最后写出x和y的关系式.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x(h)
12
15
17
22
关系式
y(km/h)
87.4
速度=路程÷时间.
x和y的积为1661,x和y成反比例
讲授新课
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 金属
相关量
金
铜
铁
锌
铝
关系式
V(cm3)
5.18
11.21
12.82
35.84
ρ(g/cm3)
19.30
7.14
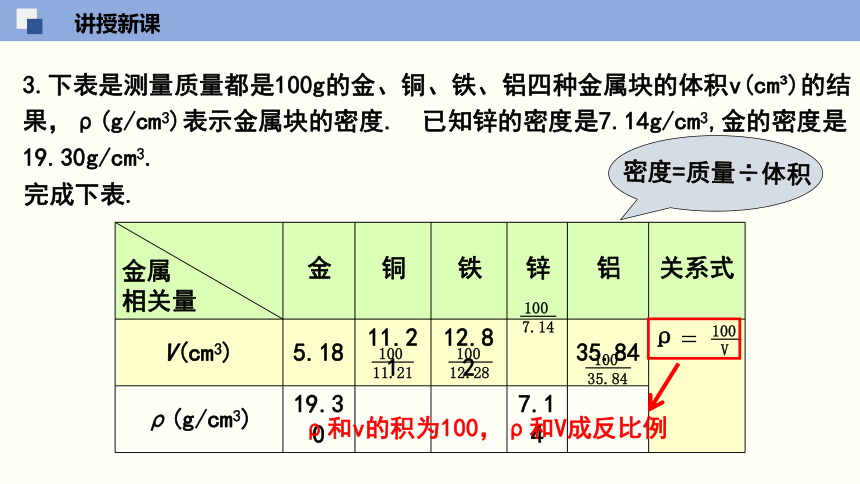
3.下表是测量质量都是100g的金、铜、铁、铝四种金属块的体积v(cm?)的结果,ρ(g/cm3)表示金属块的密度. 已知锌的密度是7.14g/cm3,金的密度是19.30g/cm3.
完成下表.
密度=质量÷体积
ρ和v的积为100,ρ和V成反比例
讲授新课
观察 ,想一想它们有什么共同点?
变量成函数关系;
都有两个变量;
两变量之积≠0,成反比例.
都具有分式的形式,其中分子是常数;
讲授新课
一般地,形如y= kx(k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
【注意】
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= kx? y=kx-1? k=xy(x≠0)?y是x的反比例函数
?
概念归纳
讲授新课
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
讲授新课
典例精析
【例1】已知y是x的反比例函数,并且当x=2时,y=6.
(1) 写出y关于x的函数解析式;
(2) 当x=4时,求y的值.
分析:因为y是x的反比例函数,所以设 ,再把x=2和y=6代入上式就可以求出常数k的值.
解:(1)设 .
因为当x=2时,y=6,所以有 . 解得k=12
因此
(2)把x=4代入 ,得
讲授新课
练一练
1. 下列函数y是不是x的反比例函数?若是,请指出 k 的值.
不是,y是x的一次函数
?
?
不是,缺少条件a≠0
是,k=3
不是,y是x的正比例函数
不是,y与x2成反比例关系
是,
是,k=2
不是,y与x-2成反比例关系
讲授新课
2. 关系式xy+4=0中y是x的反比例函数吗?若是,k等于多少?若不是,请说明理由。
k等于 -4
∴ y是x的反比例函数
?
讲授新课
知识点二 确定反比例函数的解析式
【例2】已知 y 是 x 的反比例函数,并且当 x=2时,y=6.
(1) 写出 y 关于 x 的函数解析式;
解:设 . 因为当 x=2时,y=6,所以有
解得 k =12.
因此
讲授新课
(2) 当 x=4 时,求 y 的值.
解:把 x=4 代入 ,得
讲授新课
练一练
1、已知:y是关于 x 的反比例函数,当x=0.3时,y =-6. 求 y 关于 x 的函数表达式和自变量 x 的取值范围.
解:
∵ y 是关于 x 的反比例函数,
解得 k =-1.8.
自变量 x 的取值范围为 x ≠0的全体实数.
∴可设 y= ( k 为常数, k ≠0).
将 x =0.3,y = -6代入 y = ,得
∴所求的函数表达式为 y = ;
讲授新课
2、已知y与x2成反比例,并且当x=3时,y=4.
(1)写出y关于x的函数解析式;
(2)求x=1.5时,求y的值;
(3)当y=6时,求x的值.
解:(1)设 ,因为当x=3时,y=4,所以有 . 解得k=36
因此 ;
(2)把x=1.5代入 ,得 ;
(3)当y=6时, ,解得 x= .
讲授新课
知识点三 建立简单的反比例函数模型
【例3】人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄. 当车速为 50km/h 时,视野为 80 度,如果视野 f (度) 是车速 v (km/h) 的反比例函数,求 f 关于 v 的函数解析式,并计算当车速为100km/h 时视野的度数.
讲授新课
当 v=100 时,f =40.
所以当车速为100km/h 时视野为40度.
解:设 . 由题意知,当 v =50时,f =80,所以
解得 k =4000.
因此
讲授新课
练一练
1、一辆汽车前灯电路上的电压保持不变,通过灯泡的电流越大,灯就越亮.设选用灯泡的电阻为R(Ω),通过的电流强度为I(A).
(1)若电阻为30 Ω,通过的电流强度为0.40 A,求I关于R的函数表达式,并说明比例系数的实际意义.
比例系数是12;实际意义:汽车前灯的电压为12 V.
解:
由欧姆定律知,I=
∴当R=30 Ω时,I=0.40 A,0.40=
∴U=0.40 ×30=12(V).
∴函数表达式为I= .
当堂检测
1.下列函数中哪些是反比例函数?哪些是一次函数?
①y=4x-1 ②y = 3x ③y= 5?2x ④ y= ?2?x??⑤ y= ?????3? ⑥-xy=3 ⑦y=6x-1
?
反比例函数
一次函数
①②⑤
③④⑥⑦
当堂检测
2. 已知函数 是反比例函数,则k必须满足 .
3. 若函数????=(m+1)x|m|﹣2是反比例函数,则????=( )
A.±1 B.±3 C.﹣1 D.1
k≠2 且 k≠-1
【详解】∵函数????=(m+1)x|m|﹣2是反比例函数,
∴|m|﹣2=﹣1且m+1≠0 ,解得:m=1.故选D.
当堂检测
4. 填空
(1) 若 是反比例函数,则 m 的取值范围是 .
(2) 若 是反比例函数,则m的取值范围是 .
(3) 若 是反比例函数,则m的取值范围是 .
m ≠ 1
m ≠ 0 且 m ≠ -2
m = -1
当堂检测
5.已知y=y1+y2,y1与x-1成正比例,y2与x成反比例,且 当x=2时y=4;x=3时y=6.求x=4时,y的值.
解:
∵ y1与x-1成正比例、y2与x成反比例
?
?
∵当x=2时y=4;x=3时y=6
?
?
?
∴
?
?
当堂检测
6.如图所示,已知菱形 ABCD 的面积为180,设它的两条对角线 AC,BD的长分别为x,y. 写出变量 y与 x 之间的关系式,并指出它是什么函数.
A
B
C
D
解:因为菱形的面积等于两条对角线长乘积的一半,
所以
所以变量 y与 x 之间的关系式为 ,
它是反比例函数.
当堂检测
7.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元?
当堂检测
解:由表中数据得xy=6400
∴y是x的反比例函数,函数解析式为y=6400????.
?
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数解析式;
当堂检测
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元?
解:由题意得(x-120)y=3200
(x-120)×6400=3200,
解得x=240
答:若商场计划每天的销售利润为3200元,则其单价应定为240元.
课堂小结
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
谢 谢~
第1课时 反比例函数
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、理解并掌握反比例函数的概念;
2、从实际问题中抽象出反比例函数的模型,能根据已知
条件确定反比例函数的解析式;
温故知新
1.函数的概念:
在一个变化过程中有( ),如果对于x的每一个值,y都有
( )的值与它对应,那么就说y是x的函数, x是( ).
2.反比例关系:
两个变量x和y
唯一
自变量
两个变量的( )是一个( )的常数,则称这两个变量成反比例.
积
不为零
新课导入
?
?
新学期伊始,小明想买一些笔记本为以后的学习做准备. 妈妈给了小明 30 元钱,小明可以如何选择笔记本的价钱和数量呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}笔记本单价x/元
1.5
2
2.5
3
5
7.5
…
购买的笔记本数量y/本
…
通过填表,你发现 x,y 之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
讲授新课
知识点一 反比例函数的概念
解:
V和t的积为2,V和t成反比例
1.小明同学家离学校 2km.小明每天骑自行车上学, 问:他骑车的速度V
(km/h)和他骑车所需的时间t(h)有怎样的数量关系?(列算式)
∵速度=路程÷时间
讲授新课
2.北京到杭州铁路线长为1161 km.一列从北京开往杭州火车,全程行驶时间为x(h),行驶平均速度为:y(km/h).
(1)完成下表;
(2)在表格最后写出x和y的关系式.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x(h)
12
15
17
22
关系式
y(km/h)
87.4
速度=路程÷时间.
x和y的积为1661,x和y成反比例
讲授新课
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 金属
相关量
金
铜
铁
锌
铝
关系式
V(cm3)
5.18
11.21
12.82
35.84
ρ(g/cm3)
19.30
7.14
3.下表是测量质量都是100g的金、铜、铁、铝四种金属块的体积v(cm?)的结果,ρ(g/cm3)表示金属块的密度. 已知锌的密度是7.14g/cm3,金的密度是19.30g/cm3.
完成下表.
密度=质量÷体积
ρ和v的积为100,ρ和V成反比例
讲授新课
观察 ,想一想它们有什么共同点?
变量成函数关系;
都有两个变量;
两变量之积≠0,成反比例.
都具有分式的形式,其中分子是常数;
讲授新课
一般地,形如y= kx(k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
【注意】
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= kx? y=kx-1? k=xy(x≠0)?y是x的反比例函数
?
概念归纳
讲授新课
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
讲授新课
典例精析
【例1】已知y是x的反比例函数,并且当x=2时,y=6.
(1) 写出y关于x的函数解析式;
(2) 当x=4时,求y的值.
分析:因为y是x的反比例函数,所以设 ,再把x=2和y=6代入上式就可以求出常数k的值.
解:(1)设 .
因为当x=2时,y=6,所以有 . 解得k=12
因此
(2)把x=4代入 ,得
讲授新课
练一练
1. 下列函数y是不是x的反比例函数?若是,请指出 k 的值.
不是,y是x的一次函数
?
?
不是,缺少条件a≠0
是,k=3
不是,y是x的正比例函数
不是,y与x2成反比例关系
是,
是,k=2
不是,y与x-2成反比例关系
讲授新课
2. 关系式xy+4=0中y是x的反比例函数吗?若是,k等于多少?若不是,请说明理由。
k等于 -4
∴ y是x的反比例函数
?
讲授新课
知识点二 确定反比例函数的解析式
【例2】已知 y 是 x 的反比例函数,并且当 x=2时,y=6.
(1) 写出 y 关于 x 的函数解析式;
解:设 . 因为当 x=2时,y=6,所以有
解得 k =12.
因此
讲授新课
(2) 当 x=4 时,求 y 的值.
解:把 x=4 代入 ,得
讲授新课
练一练
1、已知:y是关于 x 的反比例函数,当x=0.3时,y =-6. 求 y 关于 x 的函数表达式和自变量 x 的取值范围.
解:
∵ y 是关于 x 的反比例函数,
解得 k =-1.8.
自变量 x 的取值范围为 x ≠0的全体实数.
∴可设 y= ( k 为常数, k ≠0).
将 x =0.3,y = -6代入 y = ,得
∴所求的函数表达式为 y = ;
讲授新课
2、已知y与x2成反比例,并且当x=3时,y=4.
(1)写出y关于x的函数解析式;
(2)求x=1.5时,求y的值;
(3)当y=6时,求x的值.
解:(1)设 ,因为当x=3时,y=4,所以有 . 解得k=36
因此 ;
(2)把x=1.5代入 ,得 ;
(3)当y=6时, ,解得 x= .
讲授新课
知识点三 建立简单的反比例函数模型
【例3】人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体是动态的,车速增加,视野变窄. 当车速为 50km/h 时,视野为 80 度,如果视野 f (度) 是车速 v (km/h) 的反比例函数,求 f 关于 v 的函数解析式,并计算当车速为100km/h 时视野的度数.
讲授新课
当 v=100 时,f =40.
所以当车速为100km/h 时视野为40度.
解:设 . 由题意知,当 v =50时,f =80,所以
解得 k =4000.
因此
讲授新课
练一练
1、一辆汽车前灯电路上的电压保持不变,通过灯泡的电流越大,灯就越亮.设选用灯泡的电阻为R(Ω),通过的电流强度为I(A).
(1)若电阻为30 Ω,通过的电流强度为0.40 A,求I关于R的函数表达式,并说明比例系数的实际意义.
比例系数是12;实际意义:汽车前灯的电压为12 V.
解:
由欧姆定律知,I=
∴当R=30 Ω时,I=0.40 A,0.40=
∴U=0.40 ×30=12(V).
∴函数表达式为I= .
当堂检测
1.下列函数中哪些是反比例函数?哪些是一次函数?
①y=4x-1 ②y = 3x ③y= 5?2x ④ y= ?2?x??⑤ y= ?????3? ⑥-xy=3 ⑦y=6x-1
?
反比例函数
一次函数
①②⑤
③④⑥⑦
当堂检测
2. 已知函数 是反比例函数,则k必须满足 .
3. 若函数????=(m+1)x|m|﹣2是反比例函数,则????=( )
A.±1 B.±3 C.﹣1 D.1
k≠2 且 k≠-1
【详解】∵函数????=(m+1)x|m|﹣2是反比例函数,
∴|m|﹣2=﹣1且m+1≠0 ,解得:m=1.故选D.
当堂检测
4. 填空
(1) 若 是反比例函数,则 m 的取值范围是 .
(2) 若 是反比例函数,则m的取值范围是 .
(3) 若 是反比例函数,则m的取值范围是 .
m ≠ 1
m ≠ 0 且 m ≠ -2
m = -1
当堂检测
5.已知y=y1+y2,y1与x-1成正比例,y2与x成反比例,且 当x=2时y=4;x=3时y=6.求x=4时,y的值.
解:
∵ y1与x-1成正比例、y2与x成反比例
?
?
∵当x=2时y=4;x=3时y=6
?
?
?
∴
?
?
当堂检测
6.如图所示,已知菱形 ABCD 的面积为180,设它的两条对角线 AC,BD的长分别为x,y. 写出变量 y与 x 之间的关系式,并指出它是什么函数.
A
B
C
D
解:因为菱形的面积等于两条对角线长乘积的一半,
所以
所以变量 y与 x 之间的关系式为 ,
它是反比例函数.
当堂检测
7.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数解析式;
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元?
当堂检测
解:由表中数据得xy=6400
∴y是x的反比例函数,函数解析式为y=6400????.
?
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数解析式;
当堂检测
(2)若商场计划每天的销售利润为3200元,则其单价应定为多少元?
解:由题意得(x-120)y=3200
(x-120)×6400=3200,
解得x=240
答:若商场计划每天的销售利润为3200元,则其单价应定为240元.
课堂小结
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
谢 谢~
