17.4 反比例函数(第2课时)课件(共28张PPT)-八年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 17.4 反比例函数(第2课时)课件(共28张PPT)-八年级数学下册同步精品课堂(华东师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 18:40:47 | ||
图片预览






文档简介
17.4 反比例函数
第2课时 反比例函数的图象与性质
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程;
2、会画反比例函数图象,了解和掌握反比例函数的图象和性质;
3、能够初步应用反比例函数的图象和性质解题;
温故知新
【提问一】什么是反比例函数?
【提问二】反比例函数的定义中需要注意什么?
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= kx? y=kx-1? k=xy(x≠0)?y是x的反比例函数
?
一般地,形如y= kx(k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
?
讲授新课
知识点一 反比例函数的图象与性质
例1 画反比例函数 与 的图象.
合作探究
提示:画函数的图象步骤一般分为:列表→描点→连线. 需要注意的是在反比例函数中自变量 x 不能为 0.
解:列表如下:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
…
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
6
4
3
2.4
2
-12
12
讲授新课
O
-2
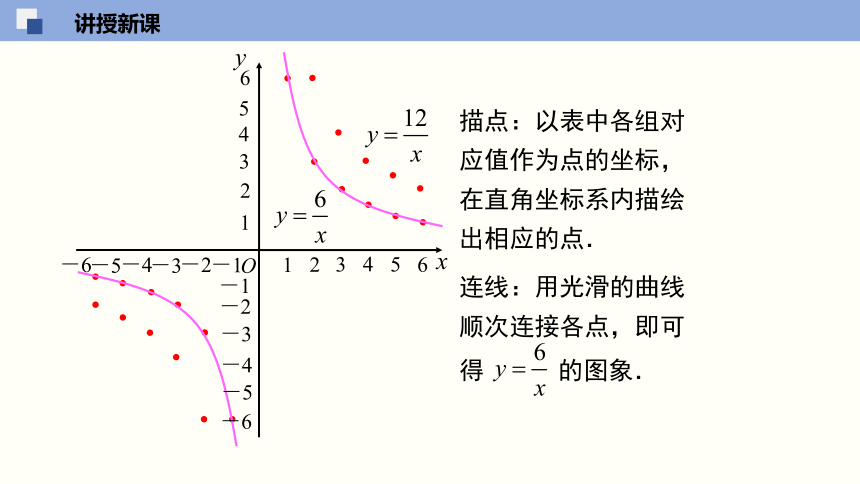
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
连线:用光滑的曲线顺次连接各点,即可
得 的图象.
讲授新课
观察这两个函数图象,回答问题:
思考:
(1) 每个函数图象分别位于哪些象限?
(2) 在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3) 对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
讲授新课
●由两条曲线组成,且分别位于第一、三象限它们与 x 轴、y 轴都不相交;
●在每个象限内,y 随 x 的增大而减小.
反比例函数 (k>0) 的图象和性质:
讲授新课
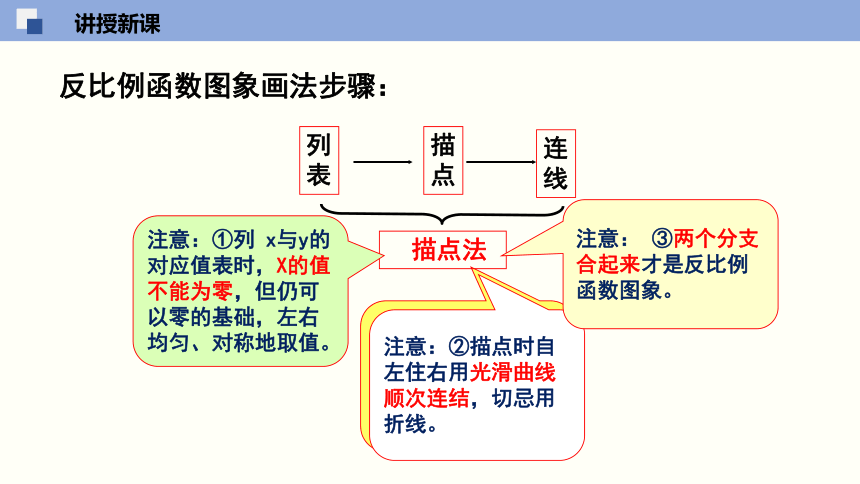
从画反比例函数图象看,描点法还应注意什么?
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
讲授新课
典例精析
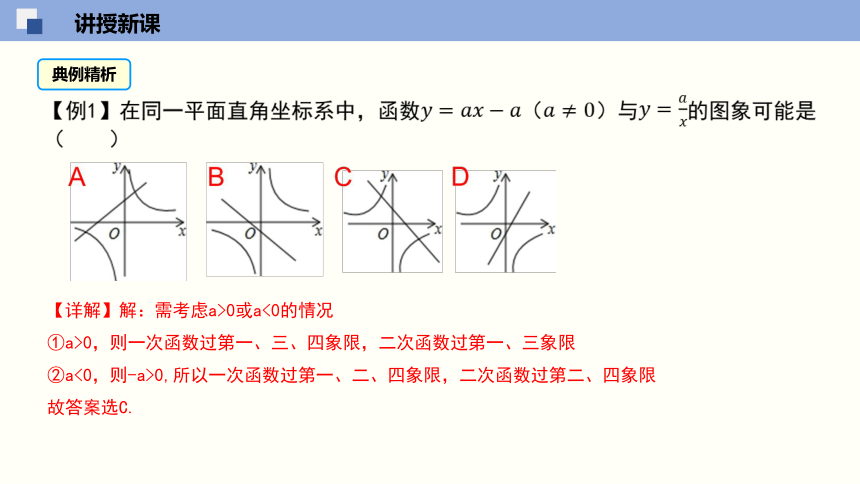
【详解】解:需考虑a>0或a<0的情况
①a>0,则一次函数过第一、三、四象限,二次函数过第一、三象限
②a<0,则-a>0,所以一次函数过第一、二、四象限,二次函数过第二、四象限
故答案选C.
【例1】在同一平面直角坐标系中,函数????=?????????????(????≠0)与????=????????的图象可能是( )
?
讲授新课
练一练
二,四
9
1
m < 4
三
讲授新课
5.若函数y=2xm?-3是反比例函数,函数图象在第二、四象限,求m的值.
解:∵该函数为反比例函数
∴m?-3=-1
又∵该函数图象在二四象限
解得m=2或m=-2.
∴m<0
∴m=-2.
讲授新课
知识点二 反比例函数的图象与性质的初步运用
【例2】已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.
讲授新课
练一练
1、已知反比例函数 在每个象限内,y 随着 x 的增大而减小,求 m 的值.
解:由题意得 m2-10=-1,且 3m-8>0.
解得 m=3.
讲授新课
2、已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
解:因为点 A (2,6) 在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
讲授新课
(2) 点B(3,4),C( , ),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为 ,因为点
A (2,6)在其图象上,所以有 ,解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上;
所以反比例函数的解析式为 .
讲授新课
(1) 图象的另一支位于哪个象限?常数 m 的取值范围
是什么?
O
x
y
3、如图,是反比例函数 图象的一支. 根据图象,回答下列问题:
解:因为这个反比例函数图象的一
支位于第一象限,所以另一支
必位于第三象限.
因为这个函数图象位于第一、
三象限,所以m-5>0,
解得m>5.
讲授新课
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和
点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的
大小关系?
解:因为 m-5 > 0,所以在这个函数图象的任一支
上,y 都随 x 的增大而减小,因此当x1>x2时,
y1<y2.
当堂检测
1.反比例函数y=-3????的大致图象是( )
?
2.下列四个点中,在反比例函数y=-6????的图象上的是( )
A.(3,-2) B.(3,2) C.(2,3) D.(-2,-3)
?
B
A
当堂检测
3.对于函数y=?3x,下列说法正确的是( )
A.当x>0时,在每一象限内,y随x的增大而增大
B.函数图象经过点3,1
C.函数图象位于第一、三象限
D.当?3<x<?1时,?3<y<?1
?
A
当堂检测
4、如图是一次函数y1=kx+b和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 .
-2
3
y
x
0
-2< x <0 或 x >3
解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,可知-23.
当堂检测
5.如图,一次函数y=kx+b与反比例函数y=mx的图像交于P(2,a)和Q
(?1,?4);
(1)求一次函数及反比例函数的表达式;
(2)根据图像,直接写出关于x的不等式mx>kx+b的解集.
?
(1)解:(1)将Q(?1,?4)代入y=mx,得m=4
∴y=4x
将P(2,a)代入y=4x,得a=2
∴P(2,2)
将Q(?1,?4)、P(2,2)代入y=kx+b得:
?
当堂检测
&?k+b=?4&2k+b=2
解得:&k=2&b=?2
故一次函数的解析式为:y=2x?2
?
(2)?????
当堂检测
6、如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
解:将B(1,4)代入y=???????? 得:m=1×4=4
∴反比例函数解析式为:y=4???? ①
将A(n,-2)代入①式得: n=-2
∴A(-2,-2)
将A(-2,-2),B(1,4)代入y=kx+b得
?
解得
∴一次函数解析式为:y=2x+2.
当堂检测
(2)求△AOB的面积.
分割法:
S△AOB =S△AOC + S△BOC
D
E
解:过A作AD⊥x轴于D,过B作BE⊥y轴于E ∵A(-2,-2),B(1,4)
∴AD=2,BE=1
在y=2x+2中,令x=0,则y=2
∴C(0,2)
∴0C=2
∴S△AOB=S△AOC+S△BOC=12×2×2+12×2×1=3.
?
当堂检测
7.如图,在平面直角坐标系中,一次函数y=?x+m的图象与反比例函数y=kx(x>0)的图象交于A、B两点,已知A(1,2)
(1)求一次函数和反比例函数的解析式;
(2)连接AO、BO,求△AOB的面积.
?
(1)解:将????(1,2)代入????=?????+??与????=????????(????>0)
中得2=?1+????,2=????,
∴????=3,????=2,
∴一次函数的解析式为????=?????+3,反比例函数的解析式为????=2????;
?
当堂检测
(2)连接AO、BO,求△AOB的面积.
(2)解:解方程组
得 或 ,
∴????(2,1);
设直线????=?????+3与????轴交于????,
当????=0时,?????+3=0,
解得:????=3,得????(3,0),
∴????△????????????=????△?????????????????△????????????=12×3×2?12×3×1=1.5.
?
课堂小结
反比例函数 (k≠0)
k
k > 0
k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
谢 谢~
第2课时 反比例函数的图象与性质
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程;
2、会画反比例函数图象,了解和掌握反比例函数的图象和性质;
3、能够初步应用反比例函数的图象和性质解题;
温故知新
【提问一】什么是反比例函数?
【提问二】反比例函数的定义中需要注意什么?
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= kx? y=kx-1? k=xy(x≠0)?y是x的反比例函数
?
一般地,形如y= kx(k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
?
讲授新课
知识点一 反比例函数的图象与性质
例1 画反比例函数 与 的图象.
合作探究
提示:画函数的图象步骤一般分为:列表→描点→连线. 需要注意的是在反比例函数中自变量 x 不能为 0.
解:列表如下:
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
…
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
-2
-2.4
-3
-4
-6
6
4
3
2.4
2
-12
12
讲授新课
O
-2
描点:以表中各组对应值作为点的坐标,在直角坐标系内描绘出相应的点.
5
6
x
y
4
3
2
1
1
2
3
4
5
6
-3
-4
-1
-5
-6
-1
-2
-3
-4
-5
-6
连线:用光滑的曲线顺次连接各点,即可
得 的图象.
讲授新课
观察这两个函数图象,回答问题:
思考:
(1) 每个函数图象分别位于哪些象限?
(2) 在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3) 对于反比例函数 (k>0),考虑问题(1)(2),你能得出同样的结论吗?
讲授新课
●由两条曲线组成,且分别位于第一、三象限它们与 x 轴、y 轴都不相交;
●在每个象限内,y 随 x 的增大而减小.
反比例函数 (k>0) 的图象和性质:
讲授新课
从画反比例函数图象看,描点法还应注意什么?
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
讲授新课
典例精析
【详解】解:需考虑a>0或a<0的情况
①a>0,则一次函数过第一、三、四象限,二次函数过第一、三象限
②a<0,则-a>0,所以一次函数过第一、二、四象限,二次函数过第二、四象限
故答案选C.
【例1】在同一平面直角坐标系中,函数????=?????????????(????≠0)与????=????????的图象可能是( )
?
讲授新课
练一练
二,四
9
1
m < 4
三
讲授新课
5.若函数y=2xm?-3是反比例函数,函数图象在第二、四象限,求m的值.
解:∵该函数为反比例函数
∴m?-3=-1
又∵该函数图象在二四象限
解得m=2或m=-2.
∴m<0
∴m=-2.
讲授新课
知识点二 反比例函数的图象与性质的初步运用
【例2】已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.
讲授新课
练一练
1、已知反比例函数 在每个象限内,y 随着 x 的增大而减小,求 m 的值.
解:由题意得 m2-10=-1,且 3m-8>0.
解得 m=3.
讲授新课
2、已知反比例函数的图象经过点 A (2,6).
(1) 这个函数的图象位于哪些象限?y 随 x 的增大如何变化?
解:因为点 A (2,6) 在第一象限,所以这个函数的
图象位于第一、三象限;
在每一个象限内,y 随 x 的增大而减小.
讲授新课
(2) 点B(3,4),C( , ),D(2,5)是否在这个
函数的图象上?
解:设这个反比例函数的解析式为 ,因为点
A (2,6)在其图象上,所以有 ,解得 k =12.
因为点 B,C 的坐标都满足该解析式,而点 D的坐标不满足,所以点 B,C 在这个函数的图象上,点 D 不在这个函数的图象上;
所以反比例函数的解析式为 .
讲授新课
(1) 图象的另一支位于哪个象限?常数 m 的取值范围
是什么?
O
x
y
3、如图,是反比例函数 图象的一支. 根据图象,回答下列问题:
解:因为这个反比例函数图象的一
支位于第一象限,所以另一支
必位于第三象限.
因为这个函数图象位于第一、
三象限,所以m-5>0,
解得m>5.
讲授新课
(2) 在这个函数图象的某一支上任取点 A (x1,y1) 和
点B (x2,y2). 如果x1>x2,那么 y1 和 y2 有怎样的
大小关系?
解:因为 m-5 > 0,所以在这个函数图象的任一支
上,y 都随 x 的增大而减小,因此当x1>x2时,
y1<y2.
当堂检测
1.反比例函数y=-3????的大致图象是( )
?
2.下列四个点中,在反比例函数y=-6????的图象上的是( )
A.(3,-2) B.(3,2) C.(2,3) D.(-2,-3)
?
B
A
当堂检测
3.对于函数y=?3x,下列说法正确的是( )
A.当x>0时,在每一象限内,y随x的增大而增大
B.函数图象经过点3,1
C.函数图象位于第一、三象限
D.当?3<x<?1时,?3<y<?1
?
A
当堂检测
4、如图是一次函数y1=kx+b和反比例函数 的图象,观察图象,当 y1﹥y2 时,x 的取值范围为 .
-2
3
y
x
0
-2< x <0 或 x >3
解析:y1﹥y2 即一次函数图象处于反比例函数图象的上方时. 观察右图,可知-2
当堂检测
5.如图,一次函数y=kx+b与反比例函数y=mx的图像交于P(2,a)和Q
(?1,?4);
(1)求一次函数及反比例函数的表达式;
(2)根据图像,直接写出关于x的不等式mx>kx+b的解集.
?
(1)解:(1)将Q(?1,?4)代入y=mx,得m=4
∴y=4x
将P(2,a)代入y=4x,得a=2
∴P(2,2)
将Q(?1,?4)、P(2,2)代入y=kx+b得:
?
当堂检测
&?k+b=?4&2k+b=2
解得:&k=2&b=?2
故一次函数的解析式为:y=2x?2
?
(2)?????
当堂检测
6、如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
解:将B(1,4)代入y=???????? 得:m=1×4=4
∴反比例函数解析式为:y=4???? ①
将A(n,-2)代入①式得: n=-2
∴A(-2,-2)
将A(-2,-2),B(1,4)代入y=kx+b得
?
解得
∴一次函数解析式为:y=2x+2.
当堂检测
(2)求△AOB的面积.
分割法:
S△AOB =S△AOC + S△BOC
D
E
解:过A作AD⊥x轴于D,过B作BE⊥y轴于E ∵A(-2,-2),B(1,4)
∴AD=2,BE=1
在y=2x+2中,令x=0,则y=2
∴C(0,2)
∴0C=2
∴S△AOB=S△AOC+S△BOC=12×2×2+12×2×1=3.
?
当堂检测
7.如图,在平面直角坐标系中,一次函数y=?x+m的图象与反比例函数y=kx(x>0)的图象交于A、B两点,已知A(1,2)
(1)求一次函数和反比例函数的解析式;
(2)连接AO、BO,求△AOB的面积.
?
(1)解:将????(1,2)代入????=?????+??与????=????????(????>0)
中得2=?1+????,2=????,
∴????=3,????=2,
∴一次函数的解析式为????=?????+3,反比例函数的解析式为????=2????;
?
当堂检测
(2)连接AO、BO,求△AOB的面积.
(2)解:解方程组
得 或 ,
∴????(2,1);
设直线????=?????+3与????轴交于????,
当????=0时,?????+3=0,
解得:????=3,得????(3,0),
∴????△????????????=????△?????????????????△????????????=12×3×2?12×3×1=1.5.
?
课堂小结
反比例函数 (k≠0)
k
k > 0
k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
谢 谢~
