17.5实践与探索(第2课时)(教学课件)-八年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 17.5实践与探索(第2课时)(教学课件)-八年级数学下册同步精品课堂(华东师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 09:18:17 | ||
图片预览









文档简介
(共35张PPT)
17.5 实践与探索
第2课时 建立一次函数模型解决实际问题
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2、有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力;
3、认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力;
导入新课
名闻遐迩的玉龙雪山,位于云南丽江城北,由12座山峰组成,主峰海拔5596m.远眺玉龙雪山,在海拔4500m处,有一条黑白分明的分界线—雪线,雪线以上是 银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
思考:1.如何理解雪线消失?
2.这段文字中有哪些数量信息?
3.这些数量之间有什么关系?
4.你能用什么方法来描述这些数量之间的关系?
导入新课
解:按照上面的假设,雪线海拔 y(m)是时间x(年)的一次函数,其函数表达式为: y=4500+10x
答:109.6年后,玉龙雪山的雪线将由现在的4500m退至山顶而消失.
当雪线退至山顶5596m时,得
4500+10x=5596
解得 x=109.6
讲授新课
知识点一 一次函数模型的应用
现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,再求出结果并讨论结果的意义.
下面有一个实际问题,你能否利用已学的知识给予解决?
讲授新课
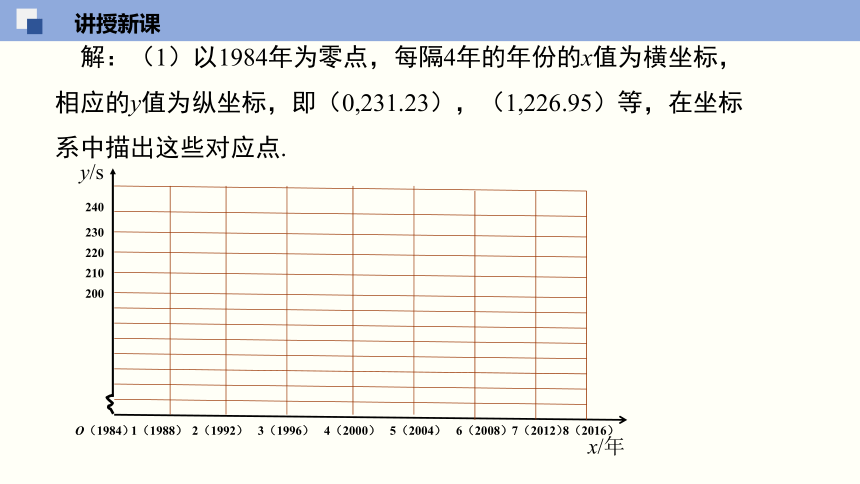
问题:奥运会每4年举办一次,奥运会的游泳成绩在不断的被刷新,如男子400m自由泳项目,2016年的奥运冠军马克-霍顿的成绩比1984年的约提高了30s,下面是该项目冠军的一些数据:
根据上面资料,能否估计2020年东京奥运会时该项目的冠军成绩?
年份 冠军成绩/s
1984 231.23
1988 226.95
1992 225.00
1996 227.97
2000 220.59
年份 冠军成绩/s
2004 223.10
2008 221.86
2012 220.14
2016 ?
2020 ?
讲授新课
解:(1)以1984年为零点,每隔4年的年份的x值为横坐标,相应的y值为纵坐标,即(0,231.23),(1,226.95)等,在坐标系中描出这些对应点.
O(1984)
230
1(1988)
2(1992)
3(1996)
4(2000)
5(2004)
6(2008)
7(2012)
8(2016)
y/s
x/年
210
220
200
240
讲授新课
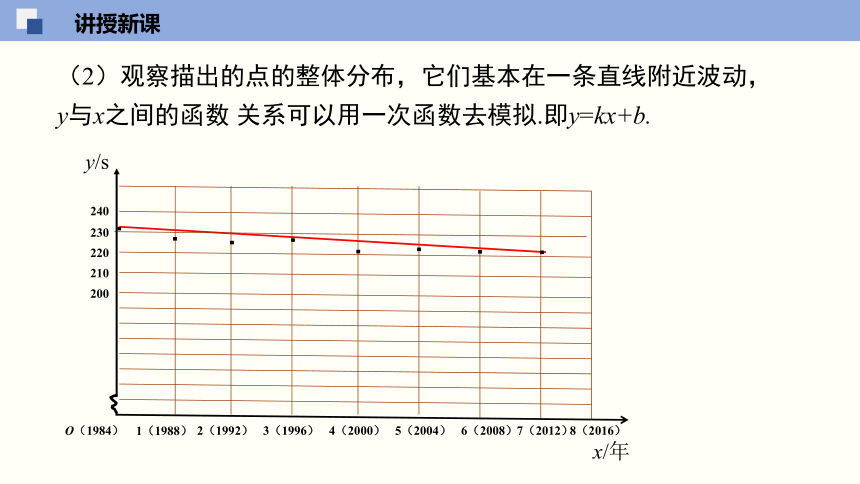
(2)观察描出的点的整体分布,它们基本在一条直线附近波动,y与x之间的函数 关系可以用一次函数去模拟.即y=kx+b.
O(1984)
230
1(1988)
2(1992)
3(1996)
4(2000)
5(2004)
6(2008)
7(2012)
8(2016)
y/s
x/年
210
220
200
240
·
·
·
·
·
·
·
·
讲授新课
这里我们选取第1个点(0,231.23)及第7个点(6,221.86)的坐标代入y=kx+b中,得
b=231.23,
6k+b=221.86.
解得k=-1.56, b=231.23
所以,一次函数的解析式为y=-1.56x+231.23.
讲授新课
(3) 当把1984年的x值作为0,以后每增加4年得x的一个值,这样2016年时的x值为8,把x=8代入上式,得y=-1.56×8+231.23=218.74(s)
因此,可以得到2016年奥运会男子的自由泳400m的冠军的成绩约是218.74s.
讲授新课
归纳总结
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.
讲授新课
练一练
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
问1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
讲授新课
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
问2:据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
这些点在一条直线上,
如图所示.
O
讲授新课
我们选取点(22,34)及
点(25,40)的坐标代入
y=kx+b中,得
22k+b=34,
25k+b=40.
解得k=2, b=-10
所以,一次函数的解析式为y=2x-10.
把x=31代入上式,得y=2×31-10=52.
因此,可以得到姚明穿52码的鞋子.
讲授新课
知识点二 一次函数的实际应用
【例1】某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12 000元,该产品的原料及加工成本合计为每件900元.
(1)写出每天的生产成本(包括固定成本和原料及加工成本)与产量之间的函数表达式;
y1=900x+12000
解:每天的生产成本y1(元)与产量x(件)之间的函数表达式是:
生产成本=固定成本+原料成本
讲授新课
(2)如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x
解:每天的销售收入y2(元)与 产量x (件)之间的函数表达式是:
当销售收入y2大于生产成本y1时,工厂有赢利,即
1200x>900x+12000
解得 x >40
销售收入 >生产成本
?
?
答:每天生产超过40件产品时,该工厂才有赢利.
讲授新课
练一练
1、在人才招聘会上,某公司承诺:应聘者被录用后第 1 年的月工资为 2 000元,在以后的一段时间内,每年的月工资比上一年的月工资增加 300元.
(1)某人在该公司连续工作n年,写出他第n年的月工资 y(元)与n的函数表达式.
解:他第n年的月工资 y (元) 与n的函数表达式是:
y=300(n-1)+2000
讲授新课
解:第 5 年的月工资为:
300×(5-1)+2000=3200(元)
所以年收入为:3200×12=38400(元)
38400<40000,所以他第5年的年收入不能超过40000元.
(2)他第5 年的年收入能否超过40 000元?
讲授新课
练一练
2.某市出租车收费标准:不超过3千米计费为7.0元, 3千米后按2.4元/千米计费.
(2)写出车费 y (元)与路程 x (千米)之间的函数表达式;
(3)小亮乘出租车出行,付费19元,计算小亮乘车的路程.
(1)当路程表显示7km时,应付费多少元?
解:7+2.4×(7-3)=16.6元
解:当0<x≤3时,y=7
当x>3时,y=7+2.4(x-3)
解:19=7+2.4(x-3) x=8km
讲授新课
3.参加英语夏令营的同学参观了一些景点,拍摄了很多照片,用了三卷胶卷. 结束后,冲洗三卷胶卷并根据同学们的需要加印照片. 已知冲洗胶卷的价格是3元/卷,加印100张以内,0.5元/张;加印超过100张可进行优惠,前100张按0.5元/张收费,超过部分按0.4元/张收费.
(2)如果去的6名同学每人加印10张,则冲印共需多少钱?如果共加印150张,则冲印共需多少钱?
解:(2) 6名同学每人加印10张,共加印10×6=60张
y=0.5×60+9=39元
加印150张,y=0.4×150+19=79元
讲授新课
(2)如果去的6名同学每人加印10张,则冲印共需多少钱?如果共加印150张,则冲印共需多少钱?
解:(2) 6名同学每人加印10张,共加印10×6=60张
y=0.5×60+9=39元
加印150张,y=0.4×150+19=79元
当堂检测
1. 某弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如图所示,当所挂物体质量为20 kg时,弹簧的长度为( )
A. 20 cm B. 25 cm C. 30 cm D.无法确定
A
O
x(kg)
y(cm)
10
10
15
当堂检测
2. “五一”期间,小海自驾去某地游玩,如图是他们汽车行驶的路程(千米)与汽车行驶时间(小时)之间的函数图象.汽车行驶2小时到达目的地,这时汽车行驶了( )千米.
A.120 B.130 C.140 D.150
O
x(小时)
y(千米)
20
100
0.5
1.5
2
C
当堂检测
3.某地电话拨号入网有两种收费方式:
A计时制:每分钟0.05元;B包月制:每月50元.
此外,每一种上网方式都要加收通信费每分钟0.02元.
某用户估计一个月上网时间为20小时,你认为他采用哪种收费方式较为合算( )
A.计时制 B.包月制 C.两种一样 D.不确定
解:设费用为y(元),上网时间为x(时). 根据题意,
计时制y1=(0.05+0.02)×60x=4.2x;包月制y2=50+0.02×60x=50+1.2x.当x=20时,计时制费用y1=4.2×20=84,包月制费用y2=50+1.2×20=74,所以一个月上网时间为20小时,采用包月制较为合算.
B
当堂检测
4.某商店今年6月初销售纯净水的数量如下表所示:
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
日期 1 2 3 4
数量(瓶) 120 125 130 135
150
解:由表可知,销售数量是日期的一次函数,设日期为x,销售数量为y,
解得
∴y=5x+115.
当x=7时,y=150,所以预测今年6月7日该商店销售纯净水的数量约为150瓶.
设y=kx+b,则有
当堂检测
5. 某种储蓄的月利率是0.2%,存入100元本金,本息和y(元)与所存月数x之间的函数表达式为_____________,若获利不少于8元,至少应存 ____个月.
y=100+0.2x
40
解: ∵存x月后的利息为100×0.2%·x,
∴y=100+100×0.2%x=100+0.2x.
由获利不少于8元,可得100×0.2%x≥8,解得x≥40,
即若获利不少于8元,至少应存40个月.
当堂检测
6.为了节能减排,我市某校准备购买某种品牌的节能灯,已知购买3只A型节能灯和5只B型节能灯共需50元,购买2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元;
解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元.根据题意,得
解得
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元.
当堂检测
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案.
解:(2)设购买A型节能灯a只, 则购买B型节能灯(200-a)只, 所需费用为w元 .根据题意,得w=5a+7(200-a)=-2a+1400. ∵a≤3(200-a),
∴a≤150.
∴a的取值范围是0∴当a=150时,w取得最小值,此时w=1100,200-a=50.答:当购买A型节能灯150只,B型节能灯50只时最省钱.
当堂检测
8.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(?)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/? 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
(2)确定y与x之间的函数表达式,并加以检验;
(3)华氏0度时的温度应是多少摄氏度?
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
当堂检测
(1)在平面直角坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
当堂检测
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
经检验,点(20,68),(30,86),
(40,104),(50,122)的坐标均能满足上述表达式,
所以y与x之间的函数表达式为
当堂检测
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
当堂检测
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:把y=x代入得,
解得
∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
谢 谢~
17.5 实践与探索
第2课时 建立一次函数模型解决实际问题
数学(华东师大版)
八年级 下册
第17章 函数及其图象
学习目标
1、巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2、有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力;
3、认识数学在现实生活中的意义,提高运用数学知识解决实际问题的能力;
导入新课
名闻遐迩的玉龙雪山,位于云南丽江城北,由12座山峰组成,主峰海拔5596m.远眺玉龙雪山,在海拔4500m处,有一条黑白分明的分界线—雪线,雪线以上是 银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
思考:1.如何理解雪线消失?
2.这段文字中有哪些数量信息?
3.这些数量之间有什么关系?
4.你能用什么方法来描述这些数量之间的关系?
导入新课
解:按照上面的假设,雪线海拔 y(m)是时间x(年)的一次函数,其函数表达式为: y=4500+10x
答:109.6年后,玉龙雪山的雪线将由现在的4500m退至山顶而消失.
当雪线退至山顶5596m时,得
4500+10x=5596
解得 x=109.6
讲授新课
知识点一 一次函数模型的应用
现实生活或具体情境中的很多问题或现象都可以抽象成数学问题,并通过建立合适的数学模型来表示数量关系和变化规律,再求出结果并讨论结果的意义.
下面有一个实际问题,你能否利用已学的知识给予解决?
讲授新课
问题:奥运会每4年举办一次,奥运会的游泳成绩在不断的被刷新,如男子400m自由泳项目,2016年的奥运冠军马克-霍顿的成绩比1984年的约提高了30s,下面是该项目冠军的一些数据:
根据上面资料,能否估计2020年东京奥运会时该项目的冠军成绩?
年份 冠军成绩/s
1984 231.23
1988 226.95
1992 225.00
1996 227.97
2000 220.59
年份 冠军成绩/s
2004 223.10
2008 221.86
2012 220.14
2016 ?
2020 ?
讲授新课
解:(1)以1984年为零点,每隔4年的年份的x值为横坐标,相应的y值为纵坐标,即(0,231.23),(1,226.95)等,在坐标系中描出这些对应点.
O(1984)
230
1(1988)
2(1992)
3(1996)
4(2000)
5(2004)
6(2008)
7(2012)
8(2016)
y/s
x/年
210
220
200
240
讲授新课
(2)观察描出的点的整体分布,它们基本在一条直线附近波动,y与x之间的函数 关系可以用一次函数去模拟.即y=kx+b.
O(1984)
230
1(1988)
2(1992)
3(1996)
4(2000)
5(2004)
6(2008)
7(2012)
8(2016)
y/s
x/年
210
220
200
240
·
·
·
·
·
·
·
·
讲授新课
这里我们选取第1个点(0,231.23)及第7个点(6,221.86)的坐标代入y=kx+b中,得
b=231.23,
6k+b=221.86.
解得k=-1.56, b=231.23
所以,一次函数的解析式为y=-1.56x+231.23.
讲授新课
(3) 当把1984年的x值作为0,以后每增加4年得x的一个值,这样2016年时的x值为8,把x=8代入上式,得y=-1.56×8+231.23=218.74(s)
因此,可以得到2016年奥运会男子的自由泳400m的冠军的成绩约是218.74s.
讲授新课
归纳总结
通过上面的学习,我们知道建立两个变量之间的函数模型,可以通过下列几个步骤完成:
(1)将实验得到的数据在直角坐标系中描出;
(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
(3)进行检验;
(4)应用这个函数模型解决问题.
讲授新课
练一练
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
问1:根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
讲授新课
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
问2:据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
这些点在一条直线上,
如图所示.
O
讲授新课
我们选取点(22,34)及
点(25,40)的坐标代入
y=kx+b中,得
22k+b=34,
25k+b=40.
解得k=2, b=-10
所以,一次函数的解析式为y=2x-10.
把x=31代入上式,得y=2×31-10=52.
因此,可以得到姚明穿52码的鞋子.
讲授新课
知识点二 一次函数的实际应用
【例1】某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12 000元,该产品的原料及加工成本合计为每件900元.
(1)写出每天的生产成本(包括固定成本和原料及加工成本)与产量之间的函数表达式;
y1=900x+12000
解:每天的生产成本y1(元)与产量x(件)之间的函数表达式是:
生产成本=固定成本+原料成本
讲授新课
(2)如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x
解:每天的销售收入y2(元)与 产量x (件)之间的函数表达式是:
当销售收入y2大于生产成本y1时,工厂有赢利,即
1200x>900x+12000
解得 x >40
销售收入 >生产成本
?
?
答:每天生产超过40件产品时,该工厂才有赢利.
讲授新课
练一练
1、在人才招聘会上,某公司承诺:应聘者被录用后第 1 年的月工资为 2 000元,在以后的一段时间内,每年的月工资比上一年的月工资增加 300元.
(1)某人在该公司连续工作n年,写出他第n年的月工资 y(元)与n的函数表达式.
解:他第n年的月工资 y (元) 与n的函数表达式是:
y=300(n-1)+2000
讲授新课
解:第 5 年的月工资为:
300×(5-1)+2000=3200(元)
所以年收入为:3200×12=38400(元)
38400<40000,所以他第5年的年收入不能超过40000元.
(2)他第5 年的年收入能否超过40 000元?
讲授新课
练一练
2.某市出租车收费标准:不超过3千米计费为7.0元, 3千米后按2.4元/千米计费.
(2)写出车费 y (元)与路程 x (千米)之间的函数表达式;
(3)小亮乘出租车出行,付费19元,计算小亮乘车的路程.
(1)当路程表显示7km时,应付费多少元?
解:7+2.4×(7-3)=16.6元
解:当0<x≤3时,y=7
当x>3时,y=7+2.4(x-3)
解:19=7+2.4(x-3) x=8km
讲授新课
3.参加英语夏令营的同学参观了一些景点,拍摄了很多照片,用了三卷胶卷. 结束后,冲洗三卷胶卷并根据同学们的需要加印照片. 已知冲洗胶卷的价格是3元/卷,加印100张以内,0.5元/张;加印超过100张可进行优惠,前100张按0.5元/张收费,超过部分按0.4元/张收费.
(2)如果去的6名同学每人加印10张,则冲印共需多少钱?如果共加印150张,则冲印共需多少钱?
解:(2) 6名同学每人加印10张,共加印10×6=60张
y=0.5×60+9=39元
加印150张,y=0.4×150+19=79元
讲授新课
(2)如果去的6名同学每人加印10张,则冲印共需多少钱?如果共加印150张,则冲印共需多少钱?
解:(2) 6名同学每人加印10张,共加印10×6=60张
y=0.5×60+9=39元
加印150张,y=0.4×150+19=79元
当堂检测
1. 某弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如图所示,当所挂物体质量为20 kg时,弹簧的长度为( )
A. 20 cm B. 25 cm C. 30 cm D.无法确定
A
O
x(kg)
y(cm)
10
10
15
当堂检测
2. “五一”期间,小海自驾去某地游玩,如图是他们汽车行驶的路程(千米)与汽车行驶时间(小时)之间的函数图象.汽车行驶2小时到达目的地,这时汽车行驶了( )千米.
A.120 B.130 C.140 D.150
O
x(小时)
y(千米)
20
100
0.5
1.5
2
C
当堂检测
3.某地电话拨号入网有两种收费方式:
A计时制:每分钟0.05元;B包月制:每月50元.
此外,每一种上网方式都要加收通信费每分钟0.02元.
某用户估计一个月上网时间为20小时,你认为他采用哪种收费方式较为合算( )
A.计时制 B.包月制 C.两种一样 D.不确定
解:设费用为y(元),上网时间为x(时). 根据题意,
计时制y1=(0.05+0.02)×60x=4.2x;包月制y2=50+0.02×60x=50+1.2x.当x=20时,计时制费用y1=4.2×20=84,包月制费用y2=50+1.2×20=74,所以一个月上网时间为20小时,采用包月制较为合算.
B
当堂检测
4.某商店今年6月初销售纯净水的数量如下表所示:
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
日期 1 2 3 4
数量(瓶) 120 125 130 135
150
解:由表可知,销售数量是日期的一次函数,设日期为x,销售数量为y,
解得
∴y=5x+115.
当x=7时,y=150,所以预测今年6月7日该商店销售纯净水的数量约为150瓶.
设y=kx+b,则有
当堂检测
5. 某种储蓄的月利率是0.2%,存入100元本金,本息和y(元)与所存月数x之间的函数表达式为_____________,若获利不少于8元,至少应存 ____个月.
y=100+0.2x
40
解: ∵存x月后的利息为100×0.2%·x,
∴y=100+100×0.2%x=100+0.2x.
由获利不少于8元,可得100×0.2%x≥8,解得x≥40,
即若获利不少于8元,至少应存40个月.
当堂检测
6.为了节能减排,我市某校准备购买某种品牌的节能灯,已知购买3只A型节能灯和5只B型节能灯共需50元,购买2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元;
解:(1)设1只A型节能灯的售价是x元,1只B型节能灯的售价是y元.根据题意,得
解得
答:1只A型节能灯的售价是5元,1只B型节能灯的售价是7元.
当堂检测
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案.
解:(2)设购买A型节能灯a只, 则购买B型节能灯(200-a)只, 所需费用为w元 .根据题意,得w=5a+7(200-a)=-2a+1400. ∵a≤3(200-a),
∴a≤150.
∴a的取值范围是0
当堂检测
8.世界上大部分国家都使用摄氏温度(℃)计量法,但美、英等国的天气预报仍然使用华氏温度(?)计量法.两种计量法之间有如下的对应关系:
x/℃ 0 10 20 30 40 50
y/? 32 50 68 86 104 122
(1)在平面直线坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
(2)确定y与x之间的函数表达式,并加以检验;
(3)华氏0度时的温度应是多少摄氏度?
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
当堂检测
(1)在平面直角坐标系中描出相应的点,观察这些点的分布情况,并猜想y与x之间的函数关系;
解:(1)如图所示,以表中对应值为坐标的点大致分布在一条直线上,据此,可猜想:y与x之间的函数关系为一次函数;
当堂检测
(2)确定y与x之间的函数表达式,并加以检验;
解:设y=kx+b,把(0,32)和(10,50)代入得
解得
经检验,点(20,68),(30,86),
(40,104),(50,122)的坐标均能满足上述表达式,
所以y与x之间的函数表达式为
当堂检测
(3)华氏0度时的温度应是多少摄氏度?
解:当y=0时,
解得
∴华氏0度时的温度应是 摄氏度;
当堂检测
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?
解:把y=x代入得,
解得
∴华氏温度的值与对应的摄氏温度的值有相等的可能,此值为-40.
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
谢 谢~
