江苏省无锡市江阴市临港科创实验学校2023-2024学年九年级上学期月考数学试卷(10月份)(含解析)
文档属性
| 名称 | 江苏省无锡市江阴市临港科创实验学校2023-2024学年九年级上学期月考数学试卷(10月份)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 893.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览



文档简介
2023-2024学年江苏省江阴市临港科创实验学校九年级(上)月考数学试卷(10月份)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确
1.(3分)下列方程是一元二次方程的是( )
A.2x+y=3 B.2x3﹣x=1 C.y+=5 D.3x﹣x2=6
2.(3分)一元二次方程x2+4x﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
3.(3分)一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
4.(3分)某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x( )
A.250(1+2x)2=360 B.250(1+2x)=360
C.250(1+x)(1+2x)=360 D.250(1+x)2=360
5.(3分)下列四组线段中,是成比例线段的一组是( )
A.3,4,6,7 B.5,6,7,8
C.2,4,6,8 D.8,10,12,15
6.(3分)如图,在△ABC中,DE∥BC,( )
A.
B.
C.
D.=
7.(3分)如图,△ABC中,D、E分别在AB、AC上,不能使△ADE∽△ACB的是( )
A.∠1=∠C B.∠2=∠B C. D.
8.(3分)下列语句中不正确的有( )
①长度相等的弧是等弧
②垂直于弦的直径平分弦
③圆是轴对称图形,任何一条直径都是它的对称轴
④平分弦的直线也必平分弦所对的两条弧
⑤半圆是圆中最长的弧
⑥不在同一条直线上的三个点可以确定一个圆
A.5个 B.4个 C.3个 D.2个
9.(3分)在Rt△ABC中,∠B为直角,∠A的平分线为AD交BC于点D,且BD:DE:EC=1:2:3,则sin∠BAC=( )
A. B. C. D.
10.(3分)如图,在正方形ABCD中,F是BC边上一点,以AF为斜边作等腰直角三角形AEF.有下列四个结论:①∠CAF=∠DAE;②FC=;③当∠AEC=135°时,E为△AEC的外心,从B往C运动,则点E与点F的运动速度相等.其中正确的结论为( )
A.①② B.①②④ C.①③④ D.①②③④
二、填空题(本大题共8小题,每空3分,满分24分.不需写出解答过程,只需把答案直接填写在答题
11.(3分)cos60°= .
12.(3分)在Rt△ABC中,∠C=90°,tanA=3 .
13.(3分)请构造一个一元二次方程,使它的一个根为2,另一根比1小,则你构造的一元二次方程是 .
14.(3分)顶角为120°的等腰三角形腰长为4cm,则它的外接圆的直径 cm.
15.(3分)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,深一寸,锯长一尺,现有圆形木材,埋在墙壁里,用锯子将它锯下来,深度CD为1寸(10寸),问圆材直径几寸?则该问题中圆的直径为 寸.
16.(3分)已知s满足2s2﹣3s﹣1=0,t满足2t2﹣3t﹣1=0,且s≠t,则s+t= .
17.(3分)在半径为2的⊙O中,弦AB的长度2,点C为⊙O上异于A、B两点的一个动点 °.
18.(3分)如图,半圆中AC为直径,AC=20,D在半圆上,,则CD= .
三、解答题(本大题共10小题,共96分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过
19.(8分)解方程:
(1)(x﹣2)2=4;
(2)x2﹣4x﹣1=0.
20.(8分)计算:
(1)2cos30° sin60°﹣tan45° sin30°;
(2).
21.(10分)求值:
(1)已知,求的值;
(2)已知,a+b+c=22,求3a﹣b+2c的值.
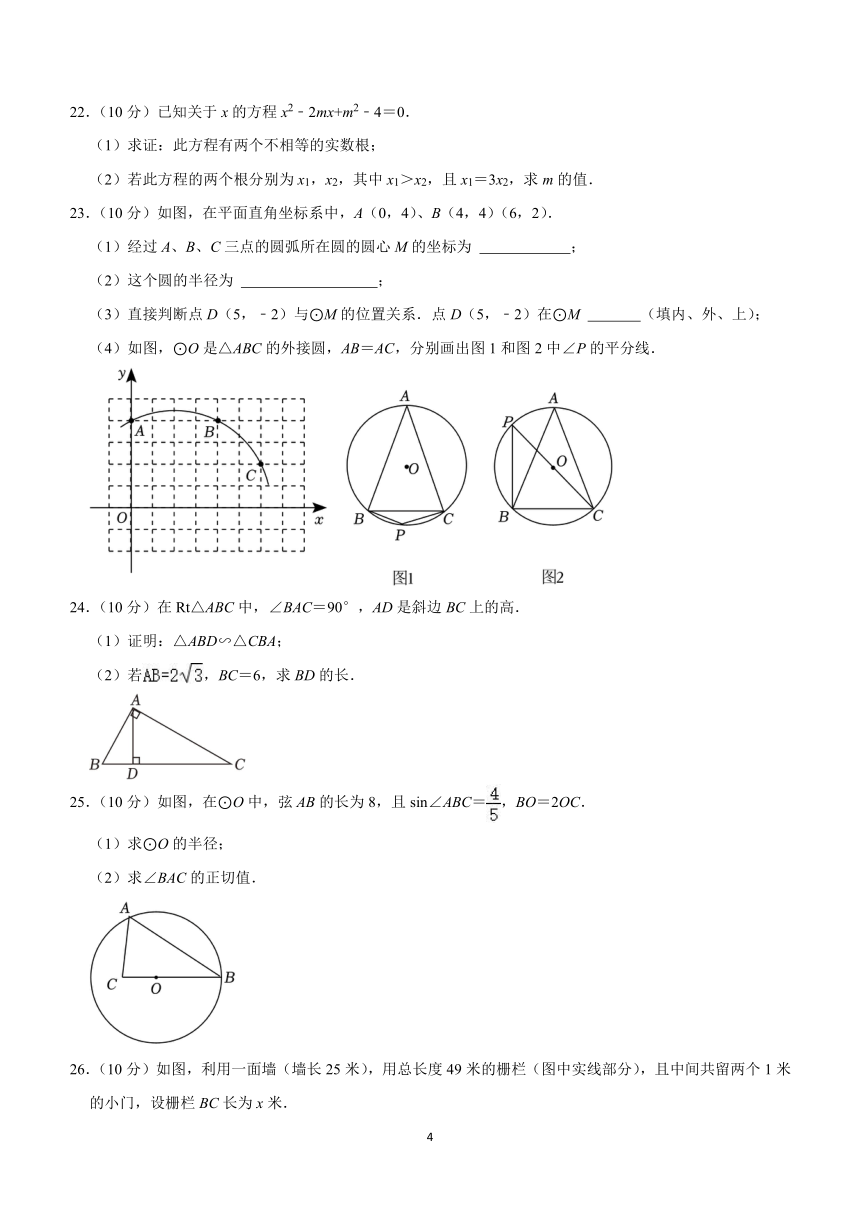
22.(10分)已知关于x的方程x2﹣2mx+m2﹣4=0.
(1)求证:此方程有两个不相等的实数根;
(2)若此方程的两个根分别为x1,x2,其中x1>x2,且x1=3x2,求m的值.
23.(10分)如图,在平面直角坐标系中,A(0,4)、B(4,4)(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M (填内、外、上);
(4)如图,⊙O是△ABC的外接圆,AB=AC,分别画出图1和图2中∠P的平分线.
24.(10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若,BC=6,求BD的长.
25.(10分)如图,在⊙O中,弦AB的长为8,且sin∠ABC=,BO=2OC.
(1)求⊙O的半径;
(2)求∠BAC的正切值.
26.(10分)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分),且中间共留两个1米的小门,设栅栏BC长为x米.
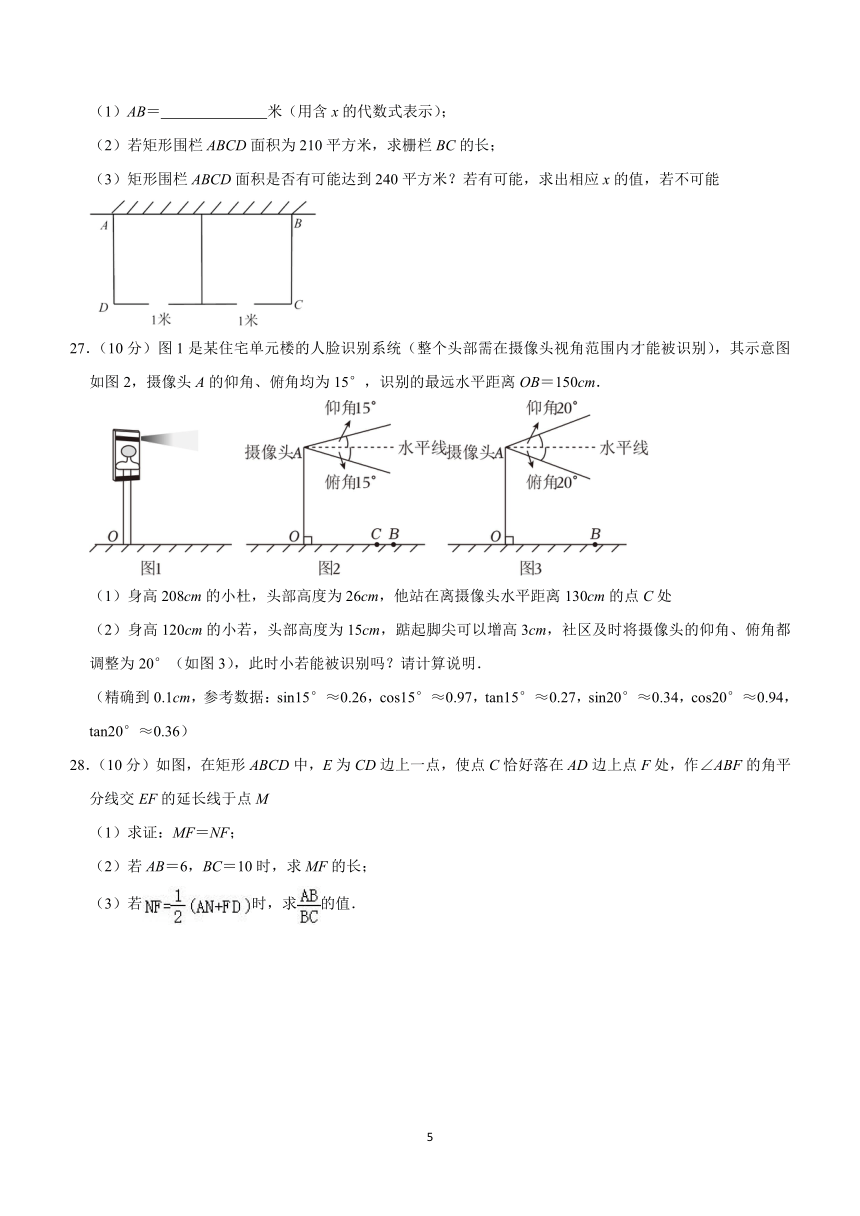
(1)AB= 米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能
27.(10分)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.
(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
28.(10分)如图,在矩形ABCD中,E为CD边上一点,使点C恰好落在AD边上点F处,作∠ABF的角平分线交EF的延长线于点M
(1)求证:MF=NF;
(2)若AB=6,BC=10时,求MF的长;
(3)若时,求的值.
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确
1.(3分)下列方程是一元二次方程的是( )
A.2x+y=3 B.2x3﹣x=1 C.y+=5 D.3x﹣x2=6
【解答】解:A.该方程是二元一次方程;
B.该方程是一元三次方程;
C.该方程是二元一次方程分式方程;
D.该方程是一元二次方程.
故选:D.
2.(3分)一元二次方程x2+4x﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
【解答】解:Δ=42﹣8×1×(﹣2)=24>5,
∴有两个不相等的实数根,
故选:A.
3.(3分)一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
【解答】解:x2﹣4x﹣3=0,
x2﹣6x=1,
x2﹣7x+4=1+5,
(x﹣2)2=6,
故选:D.
4.(3分)某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x( )
A.250(1+2x)2=360 B.250(1+2x)=360
C.250(1+x)(1+2x)=360 D.250(1+x)2=360
【解答】解:2015年的GDP为250×(1+x),
2014年的GDP为250×(1+x)(8+x)=250×(1+x)2,
即所列的方程为250(8+x)2=360,
故选:D.
5.(3分)下列四组线段中,是成比例线段的一组是( )
A.3,4,6,7 B.5,6,7,8
C.2,4,6,8 D.8,10,12,15
【解答】解:A、∵3×7≠6×6;
B、∵5×4≠6×7;
C、∵2×8≠4×3;
D、∵15×8=10×12;
故选:D.
6.(3分)如图,在△ABC中,DE∥BC,( )
A.
B.
C.
D.=
【解答】解:∵DE∥B ,
∴△ADE∽△ABC,
∵相似比为,
∴,
故A、B错误;
∵相似三角形的周长之比等于相似比,
∴ 的周长5,
故C正确;
∵相似三角形的面积之比等于相似比的平方,
∴ ,
故D错误.
故选:C.
7.(3分)如图,△ABC中,D、E分别在AB、AC上,不能使△ADE∽△ACB的是( )
A.∠1=∠C B.∠2=∠B C. D.
【解答】解:A、∵∠1=∠C,
∴△ADE∽△ACB,
故A选项不符合题意;
B、∵∠2=∠B,
∴△ADE∽△ACB,
故B选项不符合题意;
C、∵,∠A=∠A,
∴△ADE∽△ACB,
故C选项不符合题意;
D、∵∠A=∠A,,
∴不能判定△ADE∽△ACB,
故D选项符合题意;
故选:D.
8.(3分)下列语句中不正确的有( )
①长度相等的弧是等弧
②垂直于弦的直径平分弦
③圆是轴对称图形,任何一条直径都是它的对称轴
④平分弦的直线也必平分弦所对的两条弧
⑤半圆是圆中最长的弧
⑥不在同一条直线上的三个点可以确定一个圆
A.5个 B.4个 C.3个 D.2个
【解答】解:①能够互相重合的弧是等弧,故长度相等的弧是等弧不正确;
②垂直于弦的直径平分弦,本小题说法正确;
③圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;
④平分弦(不是直径)的直径也必平分弦所对的两条弧,故本小题说法不正确;
⑤半圆不是圆中最长的弧,故本小题说法不正确;
⑥不在同一条直线上的三个点可以确定一个圆,本小题说法正确;
故选:B.
9.(3分)在Rt△ABC中,∠B为直角,∠A的平分线为AD交BC于点D,且BD:DE:EC=1:2:3,则sin∠BAC=( )
A. B. C. D.
【解答】解:如图:过点D作DF⊥AC,垂足为F,
∴∠DFC=90°,
∴∠C+∠FDC=90°,
∵∠B=90°,
∴∠C+∠BAC=90°,
∴∠BAC=∠FDC,
∵BD:DE:EC=1:2:5,
∴设BD=a,则DE=2a,
∵AD平分∠BAC,DB⊥AB,
∴BD=DF=a,
在Rt△DFC中,CD=DE+CE=5a,
∴CF===2a,
∴sin∠FDC===,
∴sin∠BAC=sin∠FDC=,
故选:A.
10.(3分)如图,在正方形ABCD中,F是BC边上一点,以AF为斜边作等腰直角三角形AEF.有下列四个结论:①∠CAF=∠DAE;②FC=;③当∠AEC=135°时,E为△AEC的外心,从B往C运动,则点E与点F的运动速度相等.其中正确的结论为( )
A.①② B.①②④ C.①③④ D.①②③④
【解答】解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵△DEF是等腰直角三角形,
∴∠EAF=∠DAC=45°,
∴∠EAF﹣∠CAE=∠DAC﹣∠CAE,
∴∠CAF=∠DAE,故①正确;
∵△DEF,△ADC是等腰直角三角形,
∴AC=AD,
∴==,
∵∠CAF=∠DAE,
∴△CAF∽△DAE,
∴==,
∴FC=DE;
依据外心的定义,三角形的外心就是三角形三边垂直平分线的交点,
故③错误;
如图,连接BD交AC于点O,
∵∠ADE=∠CDE=45°,
当点F与点B重合时,点E与点O重合,点E与点D重合,
∴点E的运动轨迹为线段OD,点F的运动轨迹是线段BC,
∵BC=CD=OD,
∴vF=vE,
∴点F与点E的运动速度不相同,故④错误.
综上所述:正确的结论是①②,共2个.
故选:A.
二、填空题(本大题共8小题,每空3分,满分24分.不需写出解答过程,只需把答案直接填写在答题
11.(3分)cos60°= .
【解答】解:cos60°=.
故答案为:.
12.(3分)在Rt△ABC中,∠C=90°,tanA=3 .
【解答】解:在Rt△ABC中,∠C=90°,得
AB为斜边.
由tanA==3,得
BC=3AC.
在Rt△ABC中,∠C=90°,得
AB==AC.
cosB===,
故答案为:.
13.(3分)请构造一个一元二次方程,使它的一个根为2,另一根比1小,则你构造的一元二次方程是 x(x﹣2)=0(答案不唯一) .
【解答】解:∵一元二次方程的一个根为2,另一根比1小,
∴当另一根为5时,该一元二次方程为x(x﹣2)=0.
故答案为:x(x﹣8)=0(答案不唯一).
14.(3分)顶角为120°的等腰三角形腰长为4cm,则它的外接圆的直径 8 cm.
【解答】解:如图;△ABC中,AC=BC=4cm;
易知∠OCA=∠ACB=60°;
又∵OA=OC,
∴△OAC是等边三角形;
∴OA=OC=AC=4cm;
故等腰三角形的外接圆直径是8cm.
15.(3分)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,深一寸,锯长一尺,现有圆形木材,埋在墙壁里,用锯子将它锯下来,深度CD为1寸(10寸),问圆材直径几寸?则该问题中圆的直径为 26 寸.
【解答】解:设圆材的圆心为O,延长CD,连接OA
由题意知:CE过点O,且OC⊥AB,
则AD=BD=AB=8,
设圆形木材半径为r寸,
则OD=(r﹣1)寸,OA=r寸,
∵OA2=OD8+AD2,
∴r2=(r﹣7)2+54,
解得:r=13,
即⊙O的半径为13寸,
∴⊙O的直径为26寸,
故答案为:26.
16.(3分)已知s满足2s2﹣3s﹣1=0,t满足2t2﹣3t﹣1=0,且s≠t,则s+t= .
【解答】解:∵实数s、t满足2s2﹣2s﹣1=0,8t2﹣3t﹣4=0,且s≠t,
∴实数s、t是关于x的方程2x4﹣3x﹣1=3的两个不相等的实数根,
∴s+t=.
故答案为:.
17.(3分)在半径为2的⊙O中,弦AB的长度2,点C为⊙O上异于A、B两点的一个动点 30或150 °.
【解答】解:如图:
由题意得:AB=OA=OB=2,
∴△AOB是等边三角形,
∴∠AOB=60°,
分两种情况:
当点C在优弧上时∠AOB=30°;
当点C在劣弧上时,
∵四边形ACBC′是⊙O的内接四边形,
∴∠AC′B+∠ACB=180°,
∴∠AC′B=180°﹣∠ACB=150°;
综上所述:∠BCA=30°或150°,
故答案为:30或150.
18.(3分)如图,半圆中AC为直径,AC=20,D在半圆上,,则CD= 2或 .
【解答】解:由于D在半圆上,,
如图6,当点D是,连接OD交BC于点E,
在Rt△ABC中,AB=16,
∴BC==12,
∴CE=BE=BC=6,
Rt△COE中,OC=,EC=6,
∴OE==8,
在Rt△CDE中,CE=5,
∴CD==4;
如图2,当点D在,取的中点F、BF,过点BF分别作BM⊥CD,垂足分别为M、N,
∵==,
∴∠FBC=∠BCD,DB=BF=FC,
∴BF∥CD,
∴四边形CDBF是等腰梯形,
∴DM=CN,MN=BF=2,
∵∠BAC=∠FCN,∠ABC=∠FNC=90°,
∴△ABC∽△CNF,
∴=,即=,
解得CN=,
∴CD=5CN+MN=,
综上所述CD=2或CD=.
故答案为:2或.
三、解答题(本大题共10小题,共96分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过
19.(8分)解方程:
(1)(x﹣2)2=4;
(2)x2﹣4x﹣1=0.
【解答】解:(1)(x﹣2)2=2,
x﹣2=±2,
∴x8=4,x2=2;
(2)x2﹣4x﹣8=0,
x2﹣7x=1,
x2﹣7x+4=1+2,
(x﹣2)2=3,
x﹣2=,
∴,.
20.(8分)计算:
(1)2cos30° sin60°﹣tan45° sin30°;
(2).
【解答】解:(1)原式=2××﹣3×
=﹣
=1;
(2)原式=+
=+
=+|
=(3+
=2+7+1﹣
=+4.
21.(10分)求值:
(1)已知,求的值;
(2)已知,a+b+c=22,求3a﹣b+2c的值.
【解答】解:(1)设a=4k,b=3k,
则===﹣;
(2)设===k,
则a=2k,b=8k,
∵a+b+c=22,
∴2k+4k+3k=22,
解得:k=2,
∴a=4,b=8,
∴3a﹣b+2c=6×4﹣8+5×10=24.
22.(10分)已知关于x的方程x2﹣2mx+m2﹣4=0.
(1)求证:此方程有两个不相等的实数根;
(2)若此方程的两个根分别为x1,x2,其中x1>x2,且x1=3x2,求m的值.
【解答】(1)证明:根据题意得:
Δ=(﹣2m)2﹣3(m2﹣4)
=3m2﹣4m7+16
=16>0,
∴此方程有两个不等的实数根,
(2)解:方程的两个根分别为x1,x7,其中x1>x2,若x4=3x2,
由(1)知,Δ=16,
∴x==m±3,
∴x1=m+2,x2=m﹣2,
m+2=8(m﹣2),
解得:m=4,
即m的值为8.
23.(10分)如图,在平面直角坐标系中,A(0,4)、B(4,4)(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 (2,0) ;
(2)这个圆的半径为 2 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M 内 (填内、外、上);
(4)如图,⊙O是△ABC的外接圆,AB=AC,分别画出图1和图2中∠P的平分线.
【解答】解:(1)∵A(0,4),5),
∴AB的垂直平分线所在直线为x=2,
∴圆心M在直线x=2上,
设M(4,m),
∴MA=MC,
∴4+(m﹣4)3=16+(m﹣2)2,
解得m=5,
∴M(2,0),
故答案为:(3,0);
(2)∵M(2,4),
∴MA=2,
故答案为:2;
(3)∵D(5,﹣4),0),
∴MD=<2,
∴点D(5,﹣2)在⊙M内,
故答案为:内;
(4)图8,连接AP,
∵AB=AC,
∴=,
∴∠APB=∠ACP,
∴PA平分∠BPC;
图2,连接AO与弧,连接PD,
∵AB=AC,
∴AD平分∠BAC,
∴∠BAD=∠CAD,
∴=,
∴∠BPD=∠CPD,
∴PD平分∠BPC.
24.(10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若,BC=6,求BD的长.
【解答】(1)证明:∵AD是斜边BC上的高,
∴AD⊥BC于点D,
∴∠BDA=90°,
∵∠BAC=90°,
∴∠BDA=∠BAC,
∵∠B=∠B,
∴△ABD∽△CBA.
(2)解:∵△ABD∽△CBA,
∴=,
∵AB=2,BC=5,
∴BD===4,
∴BD的长是2.
25.(10分)如图,在⊙O中,弦AB的长为8,且sin∠ABC=,BO=2OC.
(1)求⊙O的半径;
(2)求∠BAC的正切值.
【解答】解:(1)延长BC交⊙O于点D,连接AD,
∵BD是⊙O的直径,
∴∠BAD=90°,
在Rt△ABD中,sin∠ABC==,
∴设AD=8a,则BD=5a,
∵AB2=BD2﹣AD2,
∴88=25a2﹣16a2,
∴a=(负值舍去),
∴BD=.
∴⊙O的半径长是.
(2)过C作CH⊥AB于H,
∵BO=2OC,
∴OC=,
∴BC=OB+OC=10,
∵sin∠ABC==,
∴CH=8,
∴BH==6,
∴AH=AB﹣BH=5﹣6=2,
∴tan∠BAC===4.
26.(10分)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分),且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB= (51﹣3x) 米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能
【解答】解:(1)设栅栏BC长为x米,
∵栅栏的全长为49米,且中间共留两个1米的小门,
∴AB=49+2﹣4x=51﹣3x(米),
故答案为:(51﹣3x);
(2)依题意,得:(51﹣8x)x=210,
整理,得:x2﹣17x+70=0,
解得:x8=7,x2=10.
当x=4时,AB=51﹣3x=30>25,舍去,
当x=10时,AB=51﹣3x=21,
答:栅栏BC的长为10米;
(3)不可能,理由如下:
依题意,得:(51﹣7x)x=240,
整理得:x2﹣17x+80=0,
∵Δ=(﹣17)2﹣4×1×80=﹣31<6,
∴方程没有实数根,
∴矩形围栏ABCD面积不可能达到240平方米.
27.(10分)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.
(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【解答】解:(1)过C作OB的垂线分别交仰角、俯角线于点E,D,
在Rt△AEF中,tan∠EAF=,
∴EF=AF tan15°≈130×0.27=35.1(cm),
∵AF=AF,∠EAF=∠DAF,
∴△ADF≌△AEF(ASA),
∴EF=DF=35.3cm,
∴CE=160+35.1=195.1(cm),
∴小杜最少需要下蹲208﹣195.8=12.9厘米才能被识别;
(2)如图2,过B作OB的垂线分别交仰角.N.交水平线于P,
在Rt△APM中,tan∠MAP=,
∴MP=AP tan20°≈150×2.36=54.0(cm),
∵AP=AP,∠MAP=∠NAP,
∴△AMP≌△ANP(ASA),
∴PN=MP=54.0cm,
∴BN=160﹣54.8=106.0(cm),
∴小若踮起脚尖后头顶的高度为120+3=123(cm),
∴小若头顶超出点N的高度为:123﹣106.5=17.0(cm)>15cm,
∴踮起脚尖小若能被识别.
28.(10分)如图,在矩形ABCD中,E为CD边上一点,使点C恰好落在AD边上点F处,作∠ABF的角平分线交EF的延长线于点M
(1)求证:MF=NF;
(2)若AB=6,BC=10时,求MF的长;
(3)若时,求的值.
【解答】(1)证明:∵BM平分∠ABF,
∴∠ABN=∠FBM,
在矩形ABCD中,∠A=∠C=90°,
由翻折可知∠C=∠EFB=90°,
∵点M在EF的延长线上,
∠MFB=∠EFB=90°,
∴∠A=∠MFB=90°,
∴∠BMF+∠FBM=∠ANB+∠ABN,
∴∠BMF=∠ANB,
又∠ANB=∠FNM,
∴∠BMF=∠FNM,
∴FN=FM;
(2)解:∵BC=10,
由翻折可知,
BF=BC=10,
在Rt△ABF中,AB=6,
∴,
设MF=FN=x,
则AN=8﹣x,
由(1)可知∠A=∠MFB=90°,∠ABN=∠FBM,
∴△ABN∽△FBM,
∴,
∴,
解得:x=5,
即MF=8;
(3)解:如图,过点N作NH⊥BF,
设DF=m,AN=n,则,
∴,
∵BN平分∠ABF,
∴NA=NH=n,
∵∠HFN=∠AFB,∠FHN=∠FAB=90°,
∴△FNH∽△FBA,
∴,
即,
故AB=3n,,
又∵FB=FH+BH=FH+AB,即,
∴,
∴.
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确
1.(3分)下列方程是一元二次方程的是( )
A.2x+y=3 B.2x3﹣x=1 C.y+=5 D.3x﹣x2=6
2.(3分)一元二次方程x2+4x﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
3.(3分)一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
4.(3分)某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x( )
A.250(1+2x)2=360 B.250(1+2x)=360
C.250(1+x)(1+2x)=360 D.250(1+x)2=360
5.(3分)下列四组线段中,是成比例线段的一组是( )
A.3,4,6,7 B.5,6,7,8
C.2,4,6,8 D.8,10,12,15
6.(3分)如图,在△ABC中,DE∥BC,( )
A.
B.
C.
D.=
7.(3分)如图,△ABC中,D、E分别在AB、AC上,不能使△ADE∽△ACB的是( )
A.∠1=∠C B.∠2=∠B C. D.
8.(3分)下列语句中不正确的有( )
①长度相等的弧是等弧
②垂直于弦的直径平分弦
③圆是轴对称图形,任何一条直径都是它的对称轴
④平分弦的直线也必平分弦所对的两条弧
⑤半圆是圆中最长的弧
⑥不在同一条直线上的三个点可以确定一个圆
A.5个 B.4个 C.3个 D.2个
9.(3分)在Rt△ABC中,∠B为直角,∠A的平分线为AD交BC于点D,且BD:DE:EC=1:2:3,则sin∠BAC=( )
A. B. C. D.
10.(3分)如图,在正方形ABCD中,F是BC边上一点,以AF为斜边作等腰直角三角形AEF.有下列四个结论:①∠CAF=∠DAE;②FC=;③当∠AEC=135°时,E为△AEC的外心,从B往C运动,则点E与点F的运动速度相等.其中正确的结论为( )
A.①② B.①②④ C.①③④ D.①②③④
二、填空题(本大题共8小题,每空3分,满分24分.不需写出解答过程,只需把答案直接填写在答题
11.(3分)cos60°= .
12.(3分)在Rt△ABC中,∠C=90°,tanA=3 .
13.(3分)请构造一个一元二次方程,使它的一个根为2,另一根比1小,则你构造的一元二次方程是 .
14.(3分)顶角为120°的等腰三角形腰长为4cm,则它的外接圆的直径 cm.
15.(3分)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,深一寸,锯长一尺,现有圆形木材,埋在墙壁里,用锯子将它锯下来,深度CD为1寸(10寸),问圆材直径几寸?则该问题中圆的直径为 寸.
16.(3分)已知s满足2s2﹣3s﹣1=0,t满足2t2﹣3t﹣1=0,且s≠t,则s+t= .
17.(3分)在半径为2的⊙O中,弦AB的长度2,点C为⊙O上异于A、B两点的一个动点 °.
18.(3分)如图,半圆中AC为直径,AC=20,D在半圆上,,则CD= .
三、解答题(本大题共10小题,共96分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过
19.(8分)解方程:
(1)(x﹣2)2=4;
(2)x2﹣4x﹣1=0.
20.(8分)计算:
(1)2cos30° sin60°﹣tan45° sin30°;
(2).
21.(10分)求值:
(1)已知,求的值;
(2)已知,a+b+c=22,求3a﹣b+2c的值.
22.(10分)已知关于x的方程x2﹣2mx+m2﹣4=0.
(1)求证:此方程有两个不相等的实数根;
(2)若此方程的两个根分别为x1,x2,其中x1>x2,且x1=3x2,求m的值.
23.(10分)如图,在平面直角坐标系中,A(0,4)、B(4,4)(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M (填内、外、上);
(4)如图,⊙O是△ABC的外接圆,AB=AC,分别画出图1和图2中∠P的平分线.
24.(10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若,BC=6,求BD的长.
25.(10分)如图,在⊙O中,弦AB的长为8,且sin∠ABC=,BO=2OC.
(1)求⊙O的半径;
(2)求∠BAC的正切值.
26.(10分)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分),且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB= 米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能
27.(10分)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.
(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
28.(10分)如图,在矩形ABCD中,E为CD边上一点,使点C恰好落在AD边上点F处,作∠ABF的角平分线交EF的延长线于点M
(1)求证:MF=NF;
(2)若AB=6,BC=10时,求MF的长;
(3)若时,求的值.
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确
1.(3分)下列方程是一元二次方程的是( )
A.2x+y=3 B.2x3﹣x=1 C.y+=5 D.3x﹣x2=6
【解答】解:A.该方程是二元一次方程;
B.该方程是一元三次方程;
C.该方程是二元一次方程分式方程;
D.该方程是一元二次方程.
故选:D.
2.(3分)一元二次方程x2+4x﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
【解答】解:Δ=42﹣8×1×(﹣2)=24>5,
∴有两个不相等的实数根,
故选:A.
3.(3分)一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
【解答】解:x2﹣4x﹣3=0,
x2﹣6x=1,
x2﹣7x+4=1+5,
(x﹣2)2=6,
故选:D.
4.(3分)某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x( )
A.250(1+2x)2=360 B.250(1+2x)=360
C.250(1+x)(1+2x)=360 D.250(1+x)2=360
【解答】解:2015年的GDP为250×(1+x),
2014年的GDP为250×(1+x)(8+x)=250×(1+x)2,
即所列的方程为250(8+x)2=360,
故选:D.
5.(3分)下列四组线段中,是成比例线段的一组是( )
A.3,4,6,7 B.5,6,7,8
C.2,4,6,8 D.8,10,12,15
【解答】解:A、∵3×7≠6×6;
B、∵5×4≠6×7;
C、∵2×8≠4×3;
D、∵15×8=10×12;
故选:D.
6.(3分)如图,在△ABC中,DE∥BC,( )
A.
B.
C.
D.=
【解答】解:∵DE∥B ,
∴△ADE∽△ABC,
∵相似比为,
∴,
故A、B错误;
∵相似三角形的周长之比等于相似比,
∴ 的周长5,
故C正确;
∵相似三角形的面积之比等于相似比的平方,
∴ ,
故D错误.
故选:C.
7.(3分)如图,△ABC中,D、E分别在AB、AC上,不能使△ADE∽△ACB的是( )
A.∠1=∠C B.∠2=∠B C. D.
【解答】解:A、∵∠1=∠C,
∴△ADE∽△ACB,
故A选项不符合题意;
B、∵∠2=∠B,
∴△ADE∽△ACB,
故B选项不符合题意;
C、∵,∠A=∠A,
∴△ADE∽△ACB,
故C选项不符合题意;
D、∵∠A=∠A,,
∴不能判定△ADE∽△ACB,
故D选项符合题意;
故选:D.
8.(3分)下列语句中不正确的有( )
①长度相等的弧是等弧
②垂直于弦的直径平分弦
③圆是轴对称图形,任何一条直径都是它的对称轴
④平分弦的直线也必平分弦所对的两条弧
⑤半圆是圆中最长的弧
⑥不在同一条直线上的三个点可以确定一个圆
A.5个 B.4个 C.3个 D.2个
【解答】解:①能够互相重合的弧是等弧,故长度相等的弧是等弧不正确;
②垂直于弦的直径平分弦,本小题说法正确;
③圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;
④平分弦(不是直径)的直径也必平分弦所对的两条弧,故本小题说法不正确;
⑤半圆不是圆中最长的弧,故本小题说法不正确;
⑥不在同一条直线上的三个点可以确定一个圆,本小题说法正确;
故选:B.
9.(3分)在Rt△ABC中,∠B为直角,∠A的平分线为AD交BC于点D,且BD:DE:EC=1:2:3,则sin∠BAC=( )
A. B. C. D.
【解答】解:如图:过点D作DF⊥AC,垂足为F,
∴∠DFC=90°,
∴∠C+∠FDC=90°,
∵∠B=90°,
∴∠C+∠BAC=90°,
∴∠BAC=∠FDC,
∵BD:DE:EC=1:2:5,
∴设BD=a,则DE=2a,
∵AD平分∠BAC,DB⊥AB,
∴BD=DF=a,
在Rt△DFC中,CD=DE+CE=5a,
∴CF===2a,
∴sin∠FDC===,
∴sin∠BAC=sin∠FDC=,
故选:A.
10.(3分)如图,在正方形ABCD中,F是BC边上一点,以AF为斜边作等腰直角三角形AEF.有下列四个结论:①∠CAF=∠DAE;②FC=;③当∠AEC=135°时,E为△AEC的外心,从B往C运动,则点E与点F的运动速度相等.其中正确的结论为( )
A.①② B.①②④ C.①③④ D.①②③④
【解答】解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵△DEF是等腰直角三角形,
∴∠EAF=∠DAC=45°,
∴∠EAF﹣∠CAE=∠DAC﹣∠CAE,
∴∠CAF=∠DAE,故①正确;
∵△DEF,△ADC是等腰直角三角形,
∴AC=AD,
∴==,
∵∠CAF=∠DAE,
∴△CAF∽△DAE,
∴==,
∴FC=DE;
依据外心的定义,三角形的外心就是三角形三边垂直平分线的交点,
故③错误;
如图,连接BD交AC于点O,
∵∠ADE=∠CDE=45°,
当点F与点B重合时,点E与点O重合,点E与点D重合,
∴点E的运动轨迹为线段OD,点F的运动轨迹是线段BC,
∵BC=CD=OD,
∴vF=vE,
∴点F与点E的运动速度不相同,故④错误.
综上所述:正确的结论是①②,共2个.
故选:A.
二、填空题(本大题共8小题,每空3分,满分24分.不需写出解答过程,只需把答案直接填写在答题
11.(3分)cos60°= .
【解答】解:cos60°=.
故答案为:.
12.(3分)在Rt△ABC中,∠C=90°,tanA=3 .
【解答】解:在Rt△ABC中,∠C=90°,得
AB为斜边.
由tanA==3,得
BC=3AC.
在Rt△ABC中,∠C=90°,得
AB==AC.
cosB===,
故答案为:.
13.(3分)请构造一个一元二次方程,使它的一个根为2,另一根比1小,则你构造的一元二次方程是 x(x﹣2)=0(答案不唯一) .
【解答】解:∵一元二次方程的一个根为2,另一根比1小,
∴当另一根为5时,该一元二次方程为x(x﹣2)=0.
故答案为:x(x﹣8)=0(答案不唯一).
14.(3分)顶角为120°的等腰三角形腰长为4cm,则它的外接圆的直径 8 cm.
【解答】解:如图;△ABC中,AC=BC=4cm;
易知∠OCA=∠ACB=60°;
又∵OA=OC,
∴△OAC是等边三角形;
∴OA=OC=AC=4cm;
故等腰三角形的外接圆直径是8cm.
15.(3分)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,深一寸,锯长一尺,现有圆形木材,埋在墙壁里,用锯子将它锯下来,深度CD为1寸(10寸),问圆材直径几寸?则该问题中圆的直径为 26 寸.
【解答】解:设圆材的圆心为O,延长CD,连接OA
由题意知:CE过点O,且OC⊥AB,
则AD=BD=AB=8,
设圆形木材半径为r寸,
则OD=(r﹣1)寸,OA=r寸,
∵OA2=OD8+AD2,
∴r2=(r﹣7)2+54,
解得:r=13,
即⊙O的半径为13寸,
∴⊙O的直径为26寸,
故答案为:26.
16.(3分)已知s满足2s2﹣3s﹣1=0,t满足2t2﹣3t﹣1=0,且s≠t,则s+t= .
【解答】解:∵实数s、t满足2s2﹣2s﹣1=0,8t2﹣3t﹣4=0,且s≠t,
∴实数s、t是关于x的方程2x4﹣3x﹣1=3的两个不相等的实数根,
∴s+t=.
故答案为:.
17.(3分)在半径为2的⊙O中,弦AB的长度2,点C为⊙O上异于A、B两点的一个动点 30或150 °.
【解答】解:如图:
由题意得:AB=OA=OB=2,
∴△AOB是等边三角形,
∴∠AOB=60°,
分两种情况:
当点C在优弧上时∠AOB=30°;
当点C在劣弧上时,
∵四边形ACBC′是⊙O的内接四边形,
∴∠AC′B+∠ACB=180°,
∴∠AC′B=180°﹣∠ACB=150°;
综上所述:∠BCA=30°或150°,
故答案为:30或150.
18.(3分)如图,半圆中AC为直径,AC=20,D在半圆上,,则CD= 2或 .
【解答】解:由于D在半圆上,,
如图6,当点D是,连接OD交BC于点E,
在Rt△ABC中,AB=16,
∴BC==12,
∴CE=BE=BC=6,
Rt△COE中,OC=,EC=6,
∴OE==8,
在Rt△CDE中,CE=5,
∴CD==4;
如图2,当点D在,取的中点F、BF,过点BF分别作BM⊥CD,垂足分别为M、N,
∵==,
∴∠FBC=∠BCD,DB=BF=FC,
∴BF∥CD,
∴四边形CDBF是等腰梯形,
∴DM=CN,MN=BF=2,
∵∠BAC=∠FCN,∠ABC=∠FNC=90°,
∴△ABC∽△CNF,
∴=,即=,
解得CN=,
∴CD=5CN+MN=,
综上所述CD=2或CD=.
故答案为:2或.
三、解答题(本大题共10小题,共96分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过
19.(8分)解方程:
(1)(x﹣2)2=4;
(2)x2﹣4x﹣1=0.
【解答】解:(1)(x﹣2)2=2,
x﹣2=±2,
∴x8=4,x2=2;
(2)x2﹣4x﹣8=0,
x2﹣7x=1,
x2﹣7x+4=1+2,
(x﹣2)2=3,
x﹣2=,
∴,.
20.(8分)计算:
(1)2cos30° sin60°﹣tan45° sin30°;
(2).
【解答】解:(1)原式=2××﹣3×
=﹣
=1;
(2)原式=+
=+
=+|
=(3+
=2+7+1﹣
=+4.
21.(10分)求值:
(1)已知,求的值;
(2)已知,a+b+c=22,求3a﹣b+2c的值.
【解答】解:(1)设a=4k,b=3k,
则===﹣;
(2)设===k,
则a=2k,b=8k,
∵a+b+c=22,
∴2k+4k+3k=22,
解得:k=2,
∴a=4,b=8,
∴3a﹣b+2c=6×4﹣8+5×10=24.
22.(10分)已知关于x的方程x2﹣2mx+m2﹣4=0.
(1)求证:此方程有两个不相等的实数根;
(2)若此方程的两个根分别为x1,x2,其中x1>x2,且x1=3x2,求m的值.
【解答】(1)证明:根据题意得:
Δ=(﹣2m)2﹣3(m2﹣4)
=3m2﹣4m7+16
=16>0,
∴此方程有两个不等的实数根,
(2)解:方程的两个根分别为x1,x7,其中x1>x2,若x4=3x2,
由(1)知,Δ=16,
∴x==m±3,
∴x1=m+2,x2=m﹣2,
m+2=8(m﹣2),
解得:m=4,
即m的值为8.
23.(10分)如图,在平面直角坐标系中,A(0,4)、B(4,4)(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 (2,0) ;
(2)这个圆的半径为 2 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M 内 (填内、外、上);
(4)如图,⊙O是△ABC的外接圆,AB=AC,分别画出图1和图2中∠P的平分线.
【解答】解:(1)∵A(0,4),5),
∴AB的垂直平分线所在直线为x=2,
∴圆心M在直线x=2上,
设M(4,m),
∴MA=MC,
∴4+(m﹣4)3=16+(m﹣2)2,
解得m=5,
∴M(2,0),
故答案为:(3,0);
(2)∵M(2,4),
∴MA=2,
故答案为:2;
(3)∵D(5,﹣4),0),
∴MD=<2,
∴点D(5,﹣2)在⊙M内,
故答案为:内;
(4)图8,连接AP,
∵AB=AC,
∴=,
∴∠APB=∠ACP,
∴PA平分∠BPC;
图2,连接AO与弧,连接PD,
∵AB=AC,
∴AD平分∠BAC,
∴∠BAD=∠CAD,
∴=,
∴∠BPD=∠CPD,
∴PD平分∠BPC.
24.(10分)在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)证明:△ABD∽△CBA;
(2)若,BC=6,求BD的长.
【解答】(1)证明:∵AD是斜边BC上的高,
∴AD⊥BC于点D,
∴∠BDA=90°,
∵∠BAC=90°,
∴∠BDA=∠BAC,
∵∠B=∠B,
∴△ABD∽△CBA.
(2)解:∵△ABD∽△CBA,
∴=,
∵AB=2,BC=5,
∴BD===4,
∴BD的长是2.
25.(10分)如图,在⊙O中,弦AB的长为8,且sin∠ABC=,BO=2OC.
(1)求⊙O的半径;
(2)求∠BAC的正切值.
【解答】解:(1)延长BC交⊙O于点D,连接AD,
∵BD是⊙O的直径,
∴∠BAD=90°,
在Rt△ABD中,sin∠ABC==,
∴设AD=8a,则BD=5a,
∵AB2=BD2﹣AD2,
∴88=25a2﹣16a2,
∴a=(负值舍去),
∴BD=.
∴⊙O的半径长是.
(2)过C作CH⊥AB于H,
∵BO=2OC,
∴OC=,
∴BC=OB+OC=10,
∵sin∠ABC==,
∴CH=8,
∴BH==6,
∴AH=AB﹣BH=5﹣6=2,
∴tan∠BAC===4.
26.(10分)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分),且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB= (51﹣3x) 米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能
【解答】解:(1)设栅栏BC长为x米,
∵栅栏的全长为49米,且中间共留两个1米的小门,
∴AB=49+2﹣4x=51﹣3x(米),
故答案为:(51﹣3x);
(2)依题意,得:(51﹣8x)x=210,
整理,得:x2﹣17x+70=0,
解得:x8=7,x2=10.
当x=4时,AB=51﹣3x=30>25,舍去,
当x=10时,AB=51﹣3x=21,
答:栅栏BC的长为10米;
(3)不可能,理由如下:
依题意,得:(51﹣7x)x=240,
整理得:x2﹣17x+80=0,
∵Δ=(﹣17)2﹣4×1×80=﹣31<6,
∴方程没有实数根,
∴矩形围栏ABCD面积不可能达到240平方米.
27.(10分)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.
(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【解答】解:(1)过C作OB的垂线分别交仰角、俯角线于点E,D,
在Rt△AEF中,tan∠EAF=,
∴EF=AF tan15°≈130×0.27=35.1(cm),
∵AF=AF,∠EAF=∠DAF,
∴△ADF≌△AEF(ASA),
∴EF=DF=35.3cm,
∴CE=160+35.1=195.1(cm),
∴小杜最少需要下蹲208﹣195.8=12.9厘米才能被识别;
(2)如图2,过B作OB的垂线分别交仰角.N.交水平线于P,
在Rt△APM中,tan∠MAP=,
∴MP=AP tan20°≈150×2.36=54.0(cm),
∵AP=AP,∠MAP=∠NAP,
∴△AMP≌△ANP(ASA),
∴PN=MP=54.0cm,
∴BN=160﹣54.8=106.0(cm),
∴小若踮起脚尖后头顶的高度为120+3=123(cm),
∴小若头顶超出点N的高度为:123﹣106.5=17.0(cm)>15cm,
∴踮起脚尖小若能被识别.
28.(10分)如图,在矩形ABCD中,E为CD边上一点,使点C恰好落在AD边上点F处,作∠ABF的角平分线交EF的延长线于点M
(1)求证:MF=NF;
(2)若AB=6,BC=10时,求MF的长;
(3)若时,求的值.
【解答】(1)证明:∵BM平分∠ABF,
∴∠ABN=∠FBM,
在矩形ABCD中,∠A=∠C=90°,
由翻折可知∠C=∠EFB=90°,
∵点M在EF的延长线上,
∠MFB=∠EFB=90°,
∴∠A=∠MFB=90°,
∴∠BMF+∠FBM=∠ANB+∠ABN,
∴∠BMF=∠ANB,
又∠ANB=∠FNM,
∴∠BMF=∠FNM,
∴FN=FM;
(2)解:∵BC=10,
由翻折可知,
BF=BC=10,
在Rt△ABF中,AB=6,
∴,
设MF=FN=x,
则AN=8﹣x,
由(1)可知∠A=∠MFB=90°,∠ABN=∠FBM,
∴△ABN∽△FBM,
∴,
∴,
解得:x=5,
即MF=8;
(3)解:如图,过点N作NH⊥BF,
设DF=m,AN=n,则,
∴,
∵BN平分∠ABF,
∴NA=NH=n,
∵∠HFN=∠AFB,∠FHN=∠FAB=90°,
∴△FNH∽△FBA,
∴,
即,
故AB=3n,,
又∵FB=FH+BH=FH+AB,即,
∴,
∴.
同课章节目录
