2023-2024学年数学人教版七年级上册 课时提高练 1.5.1 课时3 有理数的综合应用(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版七年级上册 课时提高练 1.5.1 课时3 有理数的综合应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 102.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览



文档简介
1.5.1 课时3 有理数的综合应用
【练基础】
必备知识1 数字规律探索
1.有这样一组有规律的数:0,3,8,15,24,35,48,63, .则横线上的数应是 ( )
A.73 B.71 C.80 D.81
2.符号“f”表示一种运算,运算结果如下:
(1)f(1)=2,f(2)=4,f(3)=6,…;
(2)f()=2,f()=3,f()=4,….
利用以上规律计算f(2026)-f()的值为 ( )
A.2027 B.2025
C.2026 D.-2026
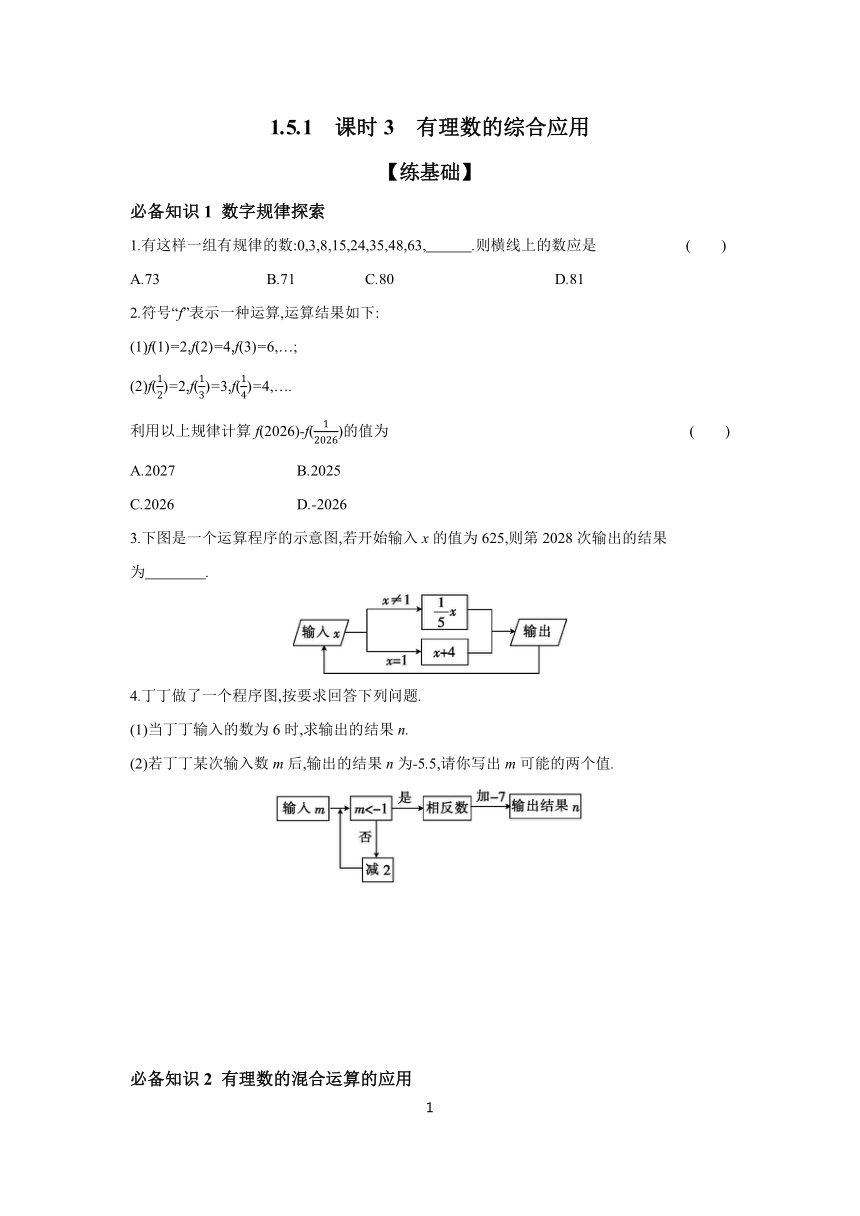
3.下图是一个运算程序的示意图,若开始输入x的值为625,则第2028次输出的结果为 .
4.丁丁做了一个程序图,按要求回答下列问题.
(1)当丁丁输入的数为6时,求输出的结果n.
(2)若丁丁某次输入数m后,输出的结果n为-5.5,请你写出m可能的两个值.
必备知识2 有理数的混合运算的应用
5.某市居民用水实行阶梯水价,实施细则如下表:
年用水量/立方米 水价/ (元/立方米)
第一阶梯 0~180(含180) 5.00
第二阶梯 180~260(含260) 7.00
第三阶梯 260以上 9.00
若某户2022年共用水280立方米,则应交水费为 ( )
A.1150元 B.1250元
C.1640元 D.2070元
6.小红和小丽利用温差测量山的高度,小红在山顶测得温度是-4 ℃,小丽此时在山脚测得温度是5 ℃.已知该地区高度每增加100米,气温降低大约0.6 ℃,这座山峰的高度大约是多少米
必备知识3 解决一些与有理数运算有关的数学问题
7.定义a※b=a2÷(b-1),例如3※5=32÷(5-1)=9÷4=,则(-3)※4的结果为 ( )
A.-3 B.3 C. D.
8.对于有理数,定义运算如下:a*b=.则3*(-4*5)= .
【练能力】
9.按照下面的操作步骤,若输入的x=-4,则输出的值为 ( )
A.3 B.-3 C.-5 D.5
10.平方等于36的数与立方等于-64的数的和是 .
11.有一种“24点”的扑克牌游戏,规则如下:任抽4张牌,用各张牌上的数和加、减、乘、除四则运算(可用括号)列一个算式,先得计算结果为“24”者获胜(J,Q,K分别表示11,12,13,A表示1).小明、小聪两人抽到的4张牌如图所示,这两组牌都能算出“24点”吗 怎样算 如果允许包含乘方运算,你能列出符合要求的不同算式吗
12.探究规律,完成相关题目.
小明说:“我定义了一种新的运算,叫*(加乘)运算.”
然后他写出了一些按照*(加乘)运算的运算法则进行运算的算式:
(+5)*(+2)=+7;(-3)*(-5)=+8;
(-3)*(+4)=-7;(+5)*(-6)=-11;
0*(+8)=8;(-6)*0=6.
小宇看了这些算式后说:“我知道你定义的*(加乘)运算的运算法则了.”
聪明的你也明白吗
(1)归纳*(加乘)运算的运算法则:
两数进行*(加乘)运算时, .
特别地,0和任何数进行*(加乘)运算,或任何数和0进行*(加乘)运算时, .
(2)计算:(-2)*[0*(-1)]= .(括号的作用与它在有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的*(加乘)运算中还适用吗 请你任选一个运算律,判断它在*(加乘)运算中是否适用,并举例验证.(举一个例子即可)
【练素养】
13.阅读材料,并解答下列问题.
如果a(a>0,a≠1)的b次幂等于N,即指数式ab=N,那么数b叫做以a为底N的对数,对数式记作logaN=b.
例如:①因为指数式22=4,所以以2为底4的对数是2,对数式记作log24=2;
②因为指数式42=16,所以以4为底16的对数是2,对数式记作log416=2.
(1)请根据上述材料将下列指数式改为对数式:
①62=36;
②43=64.
(2)将下列对数式改为指数式:
①log525=2;
②log327=3.
(3)计算:log232.
参考答案
练基础
1.C 2.C
3.1
4.【解析】(1)根据题意,得6-2=4,4-2=2,2-2=0,0-2=-2,-2的相反数是2,2-7=-5,则输出的结果n=-5.
(2)m可能的值为-1.5或0.5.(答案不唯一)
5.C
6.【解析】根据题意,得[5-(-4)]÷0.6×100=1500(米),所以这座山峰的高度大约是1500米.
7.B
8.
练能力
9.C
10.2或-10
11.【解析】小明、小聪抽到的牌都能算出“24”点,如(3+4+5)×2=24,11×2+10÷5=24.如果允许包含乘方运算,可列算式如52-4+3=24,52-11+10=24(答案不唯一).
12.【解析】(1)同号得正,异号得负,并把绝对值相加.
结果等于这个数的绝对值.
(2)-3.
(3)加法交换律和加法结合律在有理数的*(加乘)运算中还适用.
由*(加乘)运算的运算法则可知,
(+5)*(+2)=+7,
(+2)*(+5)=+7,
所以(+5)*(+2)=(+2)*(+5),
即加法交换律在有理数的*(加乘)运算中还适用.
练素养
13.【解析】(1)①62=36,
对数式记作log636=2;
②43=64,
对数式记作log464=3.
(2)①log525=2,
指数式为52=25;
②log327=3,
指数式为33=27.
(3)因为25=32,
所以log232=5.
2
【练基础】
必备知识1 数字规律探索
1.有这样一组有规律的数:0,3,8,15,24,35,48,63, .则横线上的数应是 ( )
A.73 B.71 C.80 D.81
2.符号“f”表示一种运算,运算结果如下:
(1)f(1)=2,f(2)=4,f(3)=6,…;
(2)f()=2,f()=3,f()=4,….
利用以上规律计算f(2026)-f()的值为 ( )
A.2027 B.2025
C.2026 D.-2026
3.下图是一个运算程序的示意图,若开始输入x的值为625,则第2028次输出的结果为 .
4.丁丁做了一个程序图,按要求回答下列问题.
(1)当丁丁输入的数为6时,求输出的结果n.
(2)若丁丁某次输入数m后,输出的结果n为-5.5,请你写出m可能的两个值.
必备知识2 有理数的混合运算的应用
5.某市居民用水实行阶梯水价,实施细则如下表:
年用水量/立方米 水价/ (元/立方米)
第一阶梯 0~180(含180) 5.00
第二阶梯 180~260(含260) 7.00
第三阶梯 260以上 9.00
若某户2022年共用水280立方米,则应交水费为 ( )
A.1150元 B.1250元
C.1640元 D.2070元
6.小红和小丽利用温差测量山的高度,小红在山顶测得温度是-4 ℃,小丽此时在山脚测得温度是5 ℃.已知该地区高度每增加100米,气温降低大约0.6 ℃,这座山峰的高度大约是多少米
必备知识3 解决一些与有理数运算有关的数学问题
7.定义a※b=a2÷(b-1),例如3※5=32÷(5-1)=9÷4=,则(-3)※4的结果为 ( )
A.-3 B.3 C. D.
8.对于有理数,定义运算如下:a*b=.则3*(-4*5)= .
【练能力】
9.按照下面的操作步骤,若输入的x=-4,则输出的值为 ( )
A.3 B.-3 C.-5 D.5
10.平方等于36的数与立方等于-64的数的和是 .
11.有一种“24点”的扑克牌游戏,规则如下:任抽4张牌,用各张牌上的数和加、减、乘、除四则运算(可用括号)列一个算式,先得计算结果为“24”者获胜(J,Q,K分别表示11,12,13,A表示1).小明、小聪两人抽到的4张牌如图所示,这两组牌都能算出“24点”吗 怎样算 如果允许包含乘方运算,你能列出符合要求的不同算式吗
12.探究规律,完成相关题目.
小明说:“我定义了一种新的运算,叫*(加乘)运算.”
然后他写出了一些按照*(加乘)运算的运算法则进行运算的算式:
(+5)*(+2)=+7;(-3)*(-5)=+8;
(-3)*(+4)=-7;(+5)*(-6)=-11;
0*(+8)=8;(-6)*0=6.
小宇看了这些算式后说:“我知道你定义的*(加乘)运算的运算法则了.”
聪明的你也明白吗
(1)归纳*(加乘)运算的运算法则:
两数进行*(加乘)运算时, .
特别地,0和任何数进行*(加乘)运算,或任何数和0进行*(加乘)运算时, .
(2)计算:(-2)*[0*(-1)]= .(括号的作用与它在有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的*(加乘)运算中还适用吗 请你任选一个运算律,判断它在*(加乘)运算中是否适用,并举例验证.(举一个例子即可)
【练素养】
13.阅读材料,并解答下列问题.
如果a(a>0,a≠1)的b次幂等于N,即指数式ab=N,那么数b叫做以a为底N的对数,对数式记作logaN=b.
例如:①因为指数式22=4,所以以2为底4的对数是2,对数式记作log24=2;
②因为指数式42=16,所以以4为底16的对数是2,对数式记作log416=2.
(1)请根据上述材料将下列指数式改为对数式:
①62=36;
②43=64.
(2)将下列对数式改为指数式:
①log525=2;
②log327=3.
(3)计算:log232.
参考答案
练基础
1.C 2.C
3.1
4.【解析】(1)根据题意,得6-2=4,4-2=2,2-2=0,0-2=-2,-2的相反数是2,2-7=-5,则输出的结果n=-5.
(2)m可能的值为-1.5或0.5.(答案不唯一)
5.C
6.【解析】根据题意,得[5-(-4)]÷0.6×100=1500(米),所以这座山峰的高度大约是1500米.
7.B
8.
练能力
9.C
10.2或-10
11.【解析】小明、小聪抽到的牌都能算出“24”点,如(3+4+5)×2=24,11×2+10÷5=24.如果允许包含乘方运算,可列算式如52-4+3=24,52-11+10=24(答案不唯一).
12.【解析】(1)同号得正,异号得负,并把绝对值相加.
结果等于这个数的绝对值.
(2)-3.
(3)加法交换律和加法结合律在有理数的*(加乘)运算中还适用.
由*(加乘)运算的运算法则可知,
(+5)*(+2)=+7,
(+2)*(+5)=+7,
所以(+5)*(+2)=(+2)*(+5),
即加法交换律在有理数的*(加乘)运算中还适用.
练素养
13.【解析】(1)①62=36,
对数式记作log636=2;
②43=64,
对数式记作log464=3.
(2)①log525=2,
指数式为52=25;
②log327=3,
指数式为33=27.
(3)因为25=32,
所以log232=5.
2
