2023-2024学年数学人教版七年级上册 课时提高练 2.2 课时3 整式的加减(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版七年级上册 课时提高练 2.2 课时3 整式的加减(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 17:20:22 | ||
图片预览


文档简介
2.2 课时3 整式的加减
【练基础】
必备知识1 整式的加减
1.下列运算正确的是 ( )
A.6x+3y=9xy B.3a2b-3ab2=0
C.3x2+2x2=5x2 D.3y2+2y2=1
2.计算:(8a-7b)-3(4a-5b)= ( )
A.-4a-8b B.-4a+8b
C.-4a-2b D.-4a-12b
3.若一个多项式加上2x2-y2等于x2+y2,则这个多项式是 ( )
A.x2-2y2 B.x2
C.-x2+2y2 D.-x2
4.若|x+y+2|+(xy-1)2=0,则(3x-xy+1)-(xy-3y-2)的值为 ( )
A.3 B.-3 C.-5 D.11
5.一个多项式加上3y2-2y-5得到多项式5y3-4y-6,则原来的多项式为 ( )
A.5y3+3y2+2y-1
B.5y3-3y2-2y-6
C.5y3+3y2-2y-1
D.5y3-3y2-2y-1
6.化简下列各式:
(1)2(x2-2xy+y2)-(x2-4xy-y2);
(2)2x3-y2+x2--x3+(x2-4y2).
7.【许昌期中】如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.
(1)求整式M.
(2)先求整式P,再自选一个喜欢的x值代入,求出P的值.
必备知识2 整式的加减的应用
8.【石家庄期末】如图,两个三角形的面积分别是6和4,对应阴影部分的面积分别是m和n,则m-n等于 ( )
A.2 B.3 C.4 D.5
9.【教材P68例7变式】一个篮球的价格为a元,一个足球的价格为b元(b>a),小明买了6个篮球和2个足球,小国买了5个篮球和3个足球,则小国比小明多花 ( )
A.(a-b)元 B.(b-a)元
C.(a-5b)元 D.(5b-a)元
【练能力】
10.设M=x2+8x+12,N=-x2+8x-3,那么M与N的大小关系是 ( )
A.MC.M>N D.无法确定
11.用棋子摆出下列一组图形
…
按照这种规律摆下去,第n个图形用的棋子个数为 ( )
A.3n B.6n C.3n+6 D.3n+3
12.先化简,再求值:-3[y-(3x2-3xy)]-[y+2(4x2-4xy)],其中x=-4,y=.
13.数学课上,老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”.甲、乙、丙、丁四位同学各有一张写有多项式的卡片,下面是甲、乙、丙、丁四位同学的对话:
请根据对话解答下列问题:
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么
【练素养】
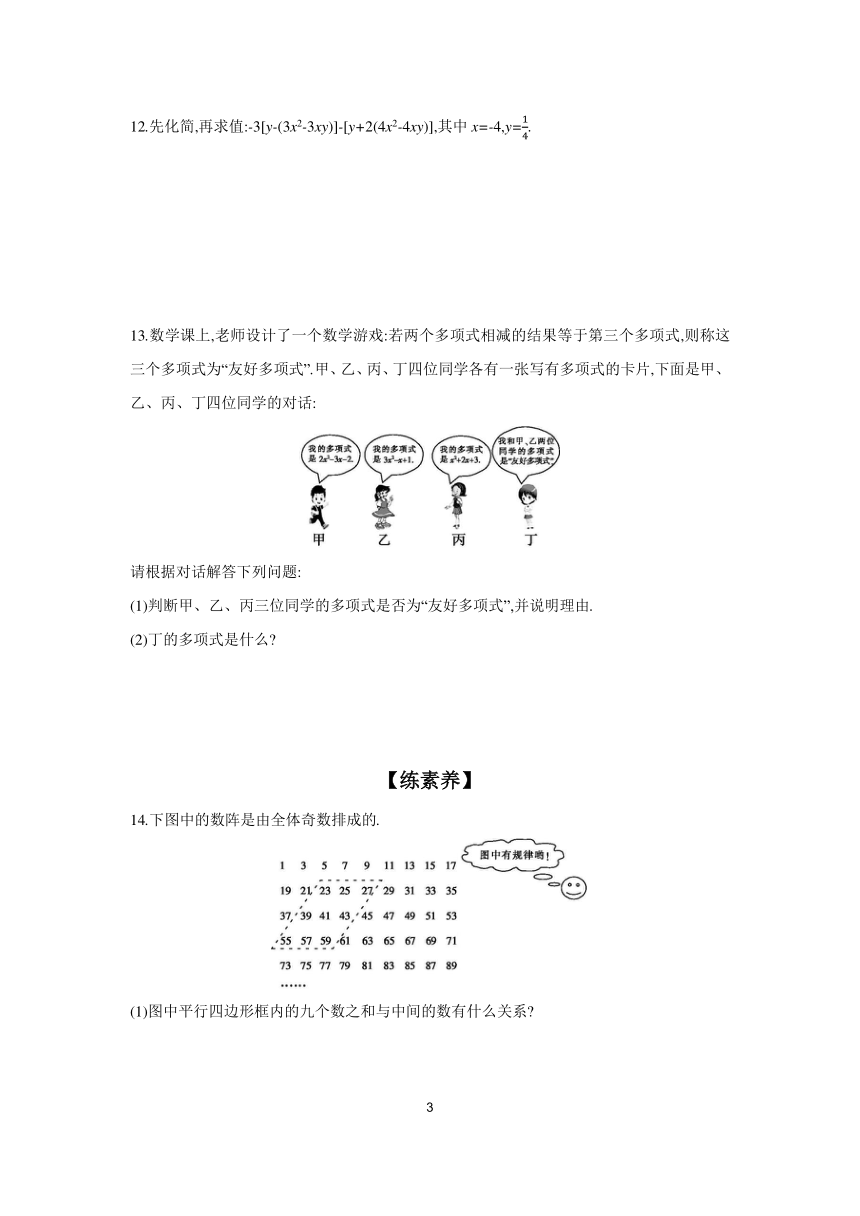
14.下图中的数阵是由全体奇数排成的.
(1)图中平行四边形框内的九个数之和与中间的数有什么关系
(2)在图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗 请说出理由.这九个数之和能等于2016吗 2015,2025呢 若能,请写出这九个数中最小的一个;若不能,请说出理由.
参考答案
练基础
1.C 2.B 3.C 4.C 5.D
6.【解析】(1)2(x2-2xy+y2)-(x2-4xy-y2)
=2x2-4xy+2y2-x2+4xy+y2
=x2+3y2.
(2)2x3-y2+x2--x3+(x2-4y2)
=2x3-2y2+x2--x3+x2-2y2
=2x3-2y2+x2+x3-x2+2y2
=3x3.
7.【解析】(1)M=2x-5-(-x2+3x-1)
=2x-5+x2-3x+1
=x2-x-4.
(2)N=3x2+2x+1+(-4x2+2x-5)
=3x2+2x+1-4x2+2x-5
=-x2+4x-4,
所以P=2x-5+(-x2+4x-4)=-x2+6x-9.
我喜欢的数是1,
所以当x=1时,原式=-1+6-9=-4.
8.A 9.B
练能力
10.C 11.D
12.【解析】原式=-3y+3(3x2-3xy)-y-2(4x2-4xy)
=-3y+9x2-9xy-y-8x2+8xy
=x2-xy-4y.
当x=-4,y=时,
原式=(-4)2-(-4)×-4×
=16+1-1
=16.
13.【解析】(1)因为(3x2-x+1)-(2x2-3x-2)
=3x2-x+1-2x2+3x+2
=x2+2x+3,
所以甲、乙、丙三位同学的多项式是“友好多项式”.
(2)因为甲、乙、丁三位同学的多项式是“友好多项式”,
所以分三种情况:
①(2x2-3x-2)-(3x2-x+1)
=2x2-3x-2-3x2+x-1
=-x2-2x-3.
②(3x2-x+1)-(2x2-3x-2)
=3x2-x+1-2x2+3x+2
=x2+2x+3.
③(3x2-x+1)+(2x2-3x-2)
=5x2-4x-1.
综上所述,丁的多项式是-x2-2x-3 或x2+2x+3或5x2-4x-1.
练素养
14.【解析】(1)平行四边形框内的九个数之和是中间的数的9倍.
(2)任意作一类似(1)中的平行四边形框,规律仍然成立.不妨设平行四边形框中间的数为n,则这九个数按大小顺序排列依次为(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).显然,其和为9n,是n的9倍,因此这九个数之和还有这种规律.
这九个数之和不能为2016.若和为2016,则9n=2016,n=224,是偶数,显然不在数阵中.这九个数之和也不能为2015.因为2015不能被9整除.这九个数之和能为2025,中间数为225,最小的数为225-18=207.
2
【练基础】
必备知识1 整式的加减
1.下列运算正确的是 ( )
A.6x+3y=9xy B.3a2b-3ab2=0
C.3x2+2x2=5x2 D.3y2+2y2=1
2.计算:(8a-7b)-3(4a-5b)= ( )
A.-4a-8b B.-4a+8b
C.-4a-2b D.-4a-12b
3.若一个多项式加上2x2-y2等于x2+y2,则这个多项式是 ( )
A.x2-2y2 B.x2
C.-x2+2y2 D.-x2
4.若|x+y+2|+(xy-1)2=0,则(3x-xy+1)-(xy-3y-2)的值为 ( )
A.3 B.-3 C.-5 D.11
5.一个多项式加上3y2-2y-5得到多项式5y3-4y-6,则原来的多项式为 ( )
A.5y3+3y2+2y-1
B.5y3-3y2-2y-6
C.5y3+3y2-2y-1
D.5y3-3y2-2y-1
6.化简下列各式:
(1)2(x2-2xy+y2)-(x2-4xy-y2);
(2)2x3-y2+x2--x3+(x2-4y2).
7.【许昌期中】如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.
(1)求整式M.
(2)先求整式P,再自选一个喜欢的x值代入,求出P的值.
必备知识2 整式的加减的应用
8.【石家庄期末】如图,两个三角形的面积分别是6和4,对应阴影部分的面积分别是m和n,则m-n等于 ( )
A.2 B.3 C.4 D.5
9.【教材P68例7变式】一个篮球的价格为a元,一个足球的价格为b元(b>a),小明买了6个篮球和2个足球,小国买了5个篮球和3个足球,则小国比小明多花 ( )
A.(a-b)元 B.(b-a)元
C.(a-5b)元 D.(5b-a)元
【练能力】
10.设M=x2+8x+12,N=-x2+8x-3,那么M与N的大小关系是 ( )
A.M
11.用棋子摆出下列一组图形
…
按照这种规律摆下去,第n个图形用的棋子个数为 ( )
A.3n B.6n C.3n+6 D.3n+3
12.先化简,再求值:-3[y-(3x2-3xy)]-[y+2(4x2-4xy)],其中x=-4,y=.
13.数学课上,老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”.甲、乙、丙、丁四位同学各有一张写有多项式的卡片,下面是甲、乙、丙、丁四位同学的对话:
请根据对话解答下列问题:
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么
【练素养】
14.下图中的数阵是由全体奇数排成的.
(1)图中平行四边形框内的九个数之和与中间的数有什么关系
(2)在图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗 请说出理由.这九个数之和能等于2016吗 2015,2025呢 若能,请写出这九个数中最小的一个;若不能,请说出理由.
参考答案
练基础
1.C 2.B 3.C 4.C 5.D
6.【解析】(1)2(x2-2xy+y2)-(x2-4xy-y2)
=2x2-4xy+2y2-x2+4xy+y2
=x2+3y2.
(2)2x3-y2+x2--x3+(x2-4y2)
=2x3-2y2+x2--x3+x2-2y2
=2x3-2y2+x2+x3-x2+2y2
=3x3.
7.【解析】(1)M=2x-5-(-x2+3x-1)
=2x-5+x2-3x+1
=x2-x-4.
(2)N=3x2+2x+1+(-4x2+2x-5)
=3x2+2x+1-4x2+2x-5
=-x2+4x-4,
所以P=2x-5+(-x2+4x-4)=-x2+6x-9.
我喜欢的数是1,
所以当x=1时,原式=-1+6-9=-4.
8.A 9.B
练能力
10.C 11.D
12.【解析】原式=-3y+3(3x2-3xy)-y-2(4x2-4xy)
=-3y+9x2-9xy-y-8x2+8xy
=x2-xy-4y.
当x=-4,y=时,
原式=(-4)2-(-4)×-4×
=16+1-1
=16.
13.【解析】(1)因为(3x2-x+1)-(2x2-3x-2)
=3x2-x+1-2x2+3x+2
=x2+2x+3,
所以甲、乙、丙三位同学的多项式是“友好多项式”.
(2)因为甲、乙、丁三位同学的多项式是“友好多项式”,
所以分三种情况:
①(2x2-3x-2)-(3x2-x+1)
=2x2-3x-2-3x2+x-1
=-x2-2x-3.
②(3x2-x+1)-(2x2-3x-2)
=3x2-x+1-2x2+3x+2
=x2+2x+3.
③(3x2-x+1)+(2x2-3x-2)
=5x2-4x-1.
综上所述,丁的多项式是-x2-2x-3 或x2+2x+3或5x2-4x-1.
练素养
14.【解析】(1)平行四边形框内的九个数之和是中间的数的9倍.
(2)任意作一类似(1)中的平行四边形框,规律仍然成立.不妨设平行四边形框中间的数为n,则这九个数按大小顺序排列依次为(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).显然,其和为9n,是n的9倍,因此这九个数之和还有这种规律.
这九个数之和不能为2016.若和为2016,则9n=2016,n=224,是偶数,显然不在数阵中.这九个数之和也不能为2015.因为2015不能被9整除.这九个数之和能为2025,中间数为225,最小的数为225-18=207.
2
