圆(山东省烟台市海阳市)
图片预览







文档简介
课件27张PPT。 圆与我们的生活息息相关,今天就让我们走进圆的世界,感受一下圆带给我们美的享受吧!
山东海阳小纪一中
刘英梅学习目标
1、知道圆的有关定义,及表示方法;
2、掌握点和圆的位置关系;
3、会根据要求画出图形。4.1车轮为什么做成圆形圆一、 创设情境 引入新课
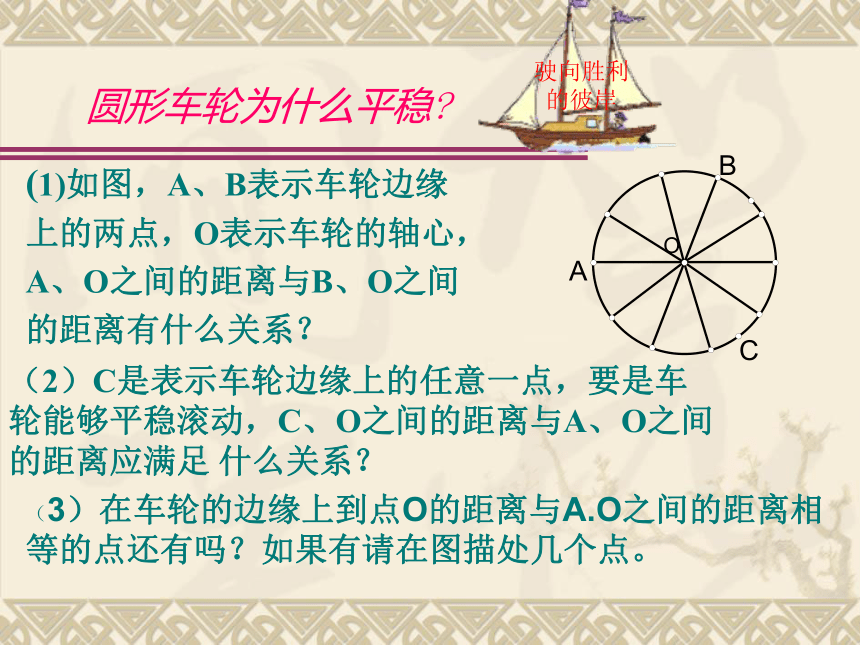
圆生活剪影一石激起千层浪奥运五环福建土楼乐在其中小憩片刻祥子圆 车轮为什么做成圆形?探索与思考:探索一车轮做成三角形、正方形可 以吗?圆形车轮为什么平稳? (2)C是表示车轮边缘上的任意一点,要是车轮能够平稳滚动,C、O之间的距离与A、O之间的距离应满足 什么关系?(1)如图,A、B表示车轮边缘
上的两点,O表示车轮的轴心,
A、O之间的距离与B、O之间
的距离有什么关系?(3)在车轮的边缘上到点O的距离与A.O之间的距离相等的点还有吗?如果有请在图描处几个点。
驶向胜利的彼岸圆形车轮为什么平稳? 车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.圆上的点到圆心的距离是一个定值 驶向胜利的彼岸投圈游戏 如果我们全班的同学同时做投圈游戏,我们该怎么站才能公平呢?画出你认为公平的示意图。
探索二: 圆的定义 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。 固定的端点O叫做圆心,线段OA叫做半径。
以点O为圆心的圆记作: 1。从圆的定义可知:圆是指圆周而不是圆面。 2、确定圆的要素是:圆心、半径。 定义1:从运动的观点看 圆心确定圆的位置,半径确定圆的大小,确定一个圆,两 者缺一不可。 “⊙O”,读作:“圆O”。定义2:从集
合的观点看
平面内到定点的距离等于定长的所有点组成的图形叫做圆等圆:半径相等的两个圆叫做等圆。两个等圆能够重合圆的有关性质战国时期的《墨经》一书中记载:“圜,一中同长也 ”。
古代的圜(huán)即圆,这句话是圆的定义,它的
意思是: 圆是从中心到周界各点有相同长度的图形。试根据圆的定义填空:
1、圆上各点到 的距离都等 于 。
2、到定点的距离等于定长的点都在 。定点(圆心)定长(半径的长)圆上一个圆将其所在的平面分成几部分?___________ 圆:圆是到定点的距离等于定长的点的集合。圆的内部:
可以看作是到圆心的距离小于半径的点的集合。
圆的外部:
可以看作是到圆心的距离大于半径的点的集合。三部分提问: 如果一个点到圆心距离小于半径, 那么这个点在哪里呢? 大于圆的半径呢? 反过来呢?●探索三:点与圆的位置关系如图,设⊙O的半径为r,A点在圆内,B点在圆上,
C点在圆外,那么OA<r, OB=r, OC> r.反过来也成立,即点的位置可以确定该点到圆心的距
离与半径的关系,反过来,已知点
到圆心的距离与半径的关系可以确
定该点到圆的位置关系。点P在⊙O上 OP=r点P在⊙O外 OP>r点P在⊙O内 OP<r(答:点A在圆上、点B在圆内、点C在圆外)画一画,想一想:2、根据图形回答下列问题:(1)看图想一想, Rt△ABC的各个顶点与⊙B在位置上有什么关系?(2)在以上三种关系中,点到圆心的距离与圆的半径在数量上有什么关系?1、画图:已知Rt△ABC,AB一块做吧!3.已知⊙O的半径r=2cm,
当OP 时,点P在⊙O上;
当OA=1cm时,点A在 ;
当OB=4cm时,点B在 。=2cm⊙O内⊙O外4. 已知:如图,矩形ABCD的对角线相交于点O,
(1) 试猜想:矩形的四个顶点在同一个圆上吗? (2)如果在同一个圆上,是在怎样一个圆上,并 给予证明?如果不在同一个圆上,试说明为什么?(以点A为圆心,2厘米长为半径的圆)(以点A为圆心,2厘米长为半径的圆的内部)(分别以点A、B为圆心,2厘米长为半径的⊙A和⊙ B的交点)(分别以点A、B为圆心,2厘米长为半径的⊙A的内部与⊙ B的内部的公共部分)小组合作: 看谁做得又快又好四 应用规律,巩固新知 如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 小组合作: 看谁做得又快又好正确答案你做对了吗?五 自我评价检测反馈:定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。 固定的端点O叫做圆心,线段OA叫做半径。1、从运动和集合的观点理解圆的定义:定义二:圆是到定点的距离等于定长的点的集合。(一)本节课你有哪些收获?还有哪些质疑?
你肯定行3、一个点到已知圆上的点的最大距离是 8,最小距离是2,则圆的半径是____1.已知⊙O的面积为25π,判断点P与⊙O的位置关系.
(1)若PO=5.5,则点P在 ;
(2) 若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上. (二)考考你:2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:到点A的距离小于2cm,且到点B的距离大于2cm4、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?5.AD.BE都是△ABC的高,试说明点A,B,D,E四点在同一个圆周上。考考你:开拓视野规矩与方圆 我国考古学者曾发掘出公元2世纪汉朝浮雕像,其中有女娲手执规,伏羲手执矩的图像;在司马迁所 写的《史记》中,也提到夏禹治水的时候“左准绳,右规矩“;在甲骨文里,就有发现有规和矩这两个字,其中规字很像一个人手执圆规在画图,矩字像两个直角,可以说极尽象形文字之妙。
“规”就是圆规,是用来画圆的工具;“矩”很像现在的直角尺,是用来画方形的工具。正如俗话说的:“不以规矩不能成方圆。”
据数学史家考证,人类最早是使用树枝来画圆的。这种原始圆规由于半径固定不变,所以只能画一种大小的圆。我国是最早给出圆的定义的国家。战国时期的《墨经》一书中记载:“圜,一中同长也 ”。古代的圜(huán)即圆,这句话是圆的定义,它的意思是:圆是圆周上的点到圆心的距离都相等的图形。这个定义和现代的定义基本相同。圆的拉绳画法就是根据《墨经》上圆的定义发明的。在适当位置钉上一个木桩,把一条大绳的一端拴在木桩上,另一头拴根木棍,拉紧大绳转上一圈儿,就可画出一个大圆。
因为圆有许多的性质,人类很早就认识了圆,使用了圆。
把车轮做成圆形的,是因为圆周上的点到圆心的距离相等,车子行驶起来平稳;还因为圆轮在滚动时摩擦力小,车子走起来省力。把碗和盆做成圆形的,一方面是圆形物体制作起来比较容易,又没棱没角损害;另一方面是用同样大小的材料做碗,圆形的碗装东西最多。把桶盖和下水道盖制成圆形,这是因为圆形的盖子,不论你用什么盖法都不会掉进里面去。而方形和椭圆形的盖子,盖的不合适,就会掉进去。有的拱形门和屋顶做成半圆形的,是因为圆形拱门抗压能力强。
圆的外形对称而和谐,我国大型舞剧《丝路花雨》在国内外演出都很成功,据舞蹈设计者介绍,主角英娘的蹈设,一招一式,举手投足,都是遵循着由圆弧组成的曲线而动,有圆的特征,因此能给人以美的享受。 三) 课外自评1、如图,⊿ABC中,∠C=90°,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
BC=3,AC=6,CD为中线,2.一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,
你准备安装几个? 怎样安装? 请说明理由.联系拓展谢谢指导再见
山东海阳小纪一中
刘英梅学习目标
1、知道圆的有关定义,及表示方法;
2、掌握点和圆的位置关系;
3、会根据要求画出图形。4.1车轮为什么做成圆形圆一、 创设情境 引入新课
圆生活剪影一石激起千层浪奥运五环福建土楼乐在其中小憩片刻祥子圆 车轮为什么做成圆形?探索与思考:探索一车轮做成三角形、正方形可 以吗?圆形车轮为什么平稳? (2)C是表示车轮边缘上的任意一点,要是车轮能够平稳滚动,C、O之间的距离与A、O之间的距离应满足 什么关系?(1)如图,A、B表示车轮边缘
上的两点,O表示车轮的轴心,
A、O之间的距离与B、O之间
的距离有什么关系?(3)在车轮的边缘上到点O的距离与A.O之间的距离相等的点还有吗?如果有请在图描处几个点。
驶向胜利的彼岸圆形车轮为什么平稳? 车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.圆上的点到圆心的距离是一个定值 驶向胜利的彼岸投圈游戏 如果我们全班的同学同时做投圈游戏,我们该怎么站才能公平呢?画出你认为公平的示意图。
探索二: 圆的定义 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆。 固定的端点O叫做圆心,线段OA叫做半径。
以点O为圆心的圆记作: 1。从圆的定义可知:圆是指圆周而不是圆面。 2、确定圆的要素是:圆心、半径。 定义1:从运动的观点看 圆心确定圆的位置,半径确定圆的大小,确定一个圆,两 者缺一不可。 “⊙O”,读作:“圆O”。定义2:从集
合的观点看
平面内到定点的距离等于定长的所有点组成的图形叫做圆等圆:半径相等的两个圆叫做等圆。两个等圆能够重合圆的有关性质战国时期的《墨经》一书中记载:“圜,一中同长也 ”。
古代的圜(huán)即圆,这句话是圆的定义,它的
意思是: 圆是从中心到周界各点有相同长度的图形。试根据圆的定义填空:
1、圆上各点到 的距离都等 于 。
2、到定点的距离等于定长的点都在 。定点(圆心)定长(半径的长)圆上一个圆将其所在的平面分成几部分?___________ 圆:圆是到定点的距离等于定长的点的集合。圆的内部:
可以看作是到圆心的距离小于半径的点的集合。
圆的外部:
可以看作是到圆心的距离大于半径的点的集合。三部分提问: 如果一个点到圆心距离小于半径, 那么这个点在哪里呢? 大于圆的半径呢? 反过来呢?●探索三:点与圆的位置关系如图,设⊙O的半径为r,A点在圆内,B点在圆上,
C点在圆外,那么OA<r, OB=r, OC> r.反过来也成立,即点的位置可以确定该点到圆心的距
离与半径的关系,反过来,已知点
到圆心的距离与半径的关系可以确
定该点到圆的位置关系。点P在⊙O上 OP=r点P在⊙O外 OP>r点P在⊙O内 OP<r(答:点A在圆上、点B在圆内、点C在圆外)画一画,想一想:2、根据图形回答下列问题:(1)看图想一想, Rt△ABC的各个顶点与⊙B在位置上有什么关系?(2)在以上三种关系中,点到圆心的距离与圆的半径在数量上有什么关系?1、画图:已知Rt△ABC,AB
当OP 时,点P在⊙O上;
当OA=1cm时,点A在 ;
当OB=4cm时,点B在 。=2cm⊙O内⊙O外4. 已知:如图,矩形ABCD的对角线相交于点O,
(1) 试猜想:矩形的四个顶点在同一个圆上吗? (2)如果在同一个圆上,是在怎样一个圆上,并 给予证明?如果不在同一个圆上,试说明为什么?(以点A为圆心,2厘米长为半径的圆)(以点A为圆心,2厘米长为半径的圆的内部)(分别以点A、B为圆心,2厘米长为半径的⊙A和⊙ B的交点)(分别以点A、B为圆心,2厘米长为半径的⊙A的内部与⊙ B的内部的公共部分)小组合作: 看谁做得又快又好四 应用规律,巩固新知 如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 小组合作: 看谁做得又快又好正确答案你做对了吗?五 自我评价检测反馈:定义一: 在同一平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫圆。 固定的端点O叫做圆心,线段OA叫做半径。1、从运动和集合的观点理解圆的定义:定义二:圆是到定点的距离等于定长的点的集合。(一)本节课你有哪些收获?还有哪些质疑?
你肯定行3、一个点到已知圆上的点的最大距离是 8,最小距离是2,则圆的半径是____1.已知⊙O的面积为25π,判断点P与⊙O的位置关系.
(1)若PO=5.5,则点P在 ;
(2) 若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上. (二)考考你:2.设AB=3厘米,画图并说明具有下列性质的点的集合是怎样的图形:到点A的距离小于2cm,且到点B的距离大于2cm4、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?5.AD.BE都是△ABC的高,试说明点A,B,D,E四点在同一个圆周上。考考你:开拓视野规矩与方圆 我国考古学者曾发掘出公元2世纪汉朝浮雕像,其中有女娲手执规,伏羲手执矩的图像;在司马迁所 写的《史记》中,也提到夏禹治水的时候“左准绳,右规矩“;在甲骨文里,就有发现有规和矩这两个字,其中规字很像一个人手执圆规在画图,矩字像两个直角,可以说极尽象形文字之妙。
“规”就是圆规,是用来画圆的工具;“矩”很像现在的直角尺,是用来画方形的工具。正如俗话说的:“不以规矩不能成方圆。”
据数学史家考证,人类最早是使用树枝来画圆的。这种原始圆规由于半径固定不变,所以只能画一种大小的圆。我国是最早给出圆的定义的国家。战国时期的《墨经》一书中记载:“圜,一中同长也 ”。古代的圜(huán)即圆,这句话是圆的定义,它的意思是:圆是圆周上的点到圆心的距离都相等的图形。这个定义和现代的定义基本相同。圆的拉绳画法就是根据《墨经》上圆的定义发明的。在适当位置钉上一个木桩,把一条大绳的一端拴在木桩上,另一头拴根木棍,拉紧大绳转上一圈儿,就可画出一个大圆。
因为圆有许多的性质,人类很早就认识了圆,使用了圆。
把车轮做成圆形的,是因为圆周上的点到圆心的距离相等,车子行驶起来平稳;还因为圆轮在滚动时摩擦力小,车子走起来省力。把碗和盆做成圆形的,一方面是圆形物体制作起来比较容易,又没棱没角损害;另一方面是用同样大小的材料做碗,圆形的碗装东西最多。把桶盖和下水道盖制成圆形,这是因为圆形的盖子,不论你用什么盖法都不会掉进里面去。而方形和椭圆形的盖子,盖的不合适,就会掉进去。有的拱形门和屋顶做成半圆形的,是因为圆形拱门抗压能力强。
圆的外形对称而和谐,我国大型舞剧《丝路花雨》在国内外演出都很成功,据舞蹈设计者介绍,主角英娘的蹈设,一招一式,举手投足,都是遵循着由圆弧组成的曲线而动,有圆的特征,因此能给人以美的享受。 三) 课外自评1、如图,⊿ABC中,∠C=90°,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
BC=3,AC=6,CD为中线,2.一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,
你准备安装几个? 怎样安装? 请说明理由.联系拓展谢谢指导再见
