2023-2024学年数学人教版七年级上册 课时提高练 4.2 课时1 直线、射线、线段(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版七年级上册 课时提高练 4.2 课时1 直线、射线、线段(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 17:34:33 | ||
图片预览


文档简介
4.2 课时1 直线、射线、线段
【练基础】
必备知识1 直线、射线、线段
1.射线OA,射线OB表示同一条射线,下面正确的是 ( )
2.如图,下列说法正确的是 ( )
A.直线AB与直线BC是同一条直线
B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线
D.射线BC与射线BA是同一条射线
3.直线、射线、线段没有粗细之分.直线 端点,向两边无限延伸;射线有 个端点,向一边无限延伸;线段有两个端点,所以线段可以 .
4.如图,在线段AB上任取D,E,C三个点,则这个图中共有 条线段.
必备知识2 两点确定一条直线
5.下列现象中,不能用基本事实“两点确定一条直线”来解释的现象是 ( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.锯木料时,一般先在木板上画两点,然后过这两点弹出一条墨迹
D.植树时,只要定出两棵树的位置就能确定同一行树所在的直线
6.经过任意三点中的两点共可以画出 ( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
7.要在墙上钉一根木条,使它不能转动,则至少需要2个钉子,主要依据是 .
8.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,说一说其中的道理.
必备知识3 点与线、线与线的位置关系
9.下列说法中,错误的是 ( )
A.经过一点的直线有无数条
B.经过两点的直线只有一条
C.一条直线上只有两个点
D.两条直线相交,只有一个交点
10.按下列语句画出图形.
(1)直线l经过A,B,C三点,点C在点A与点B之间.
(2)经过点O的三条直线a,b,c.
(3)两条直线AB与CD相交于点P.
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
【练能力】
11.下列说法中错误的是 ( )
A.过一点可以作无数条直线
B.过已知三点可以画一条直线
C.一条直线通过无数个点
D.两点确定一条直线
12.【保定期末】《红楼梦》第57回有这么一句话,“自古道:‘千里姻缘一线牵’,管姻缘的有一位月下老儿,预先注定,暗里只用一根红线,把这两个人的脚绊住.”请问,这里所说的“线”若是真的,则在数学中指的应是 ( )
A.直线 B.射线
C.线段 D.以上都不对
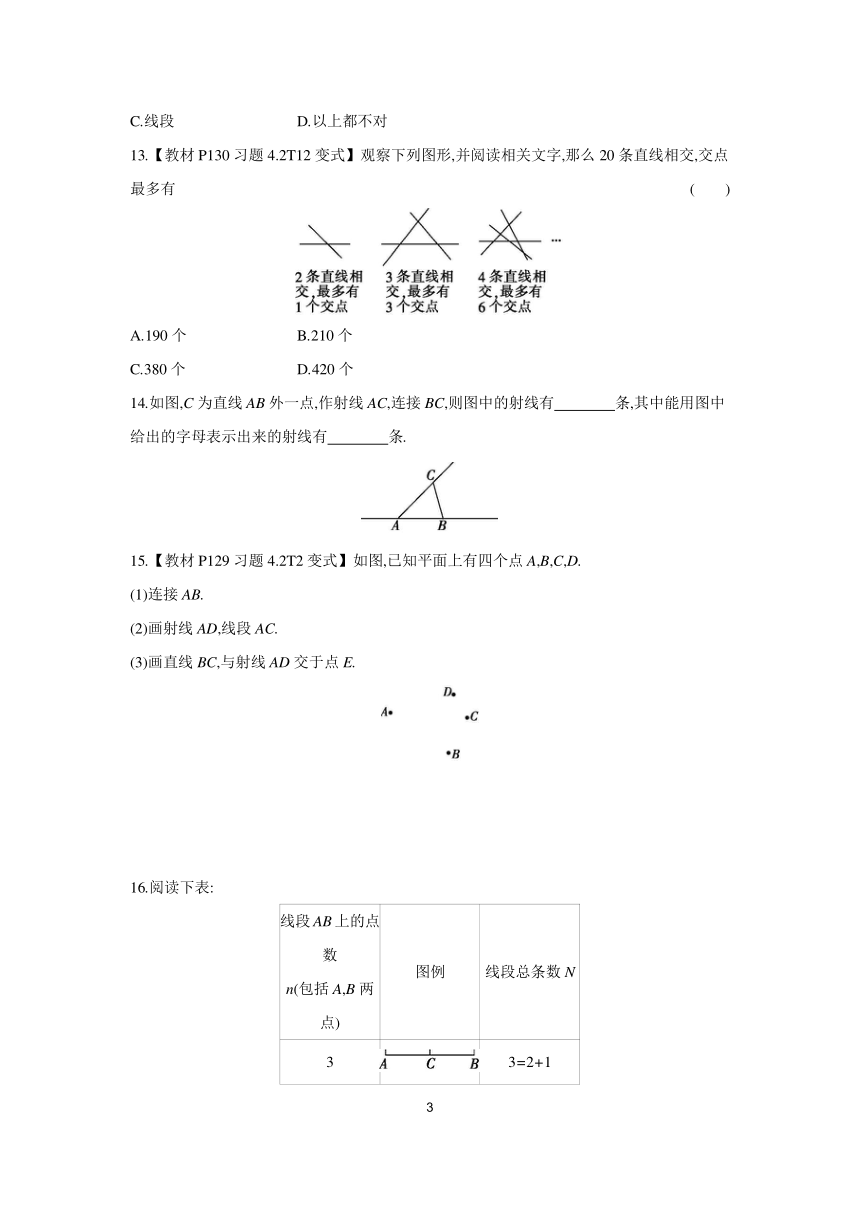
13.【教材P130习题4.2T12变式】观察下列图形,并阅读相关文字,那么20条直线相交,交点最多有 ( )
A.190个 B.210个
C.380个 D.420个
14.如图,C为直线AB外一点,作射线AC,连接BC,则图中的射线有 条,其中能用图中给出的字母表示出来的射线有 条.
15.【教材P129习题4.2T2变式】如图,已知平面上有四个点A,B,C,D.
(1)连接AB.
(2)画射线AD,线段AC.
(3)画直线BC,与射线AD交于点E.
16.阅读下表:
线段AB上的点数 n(包括A,B两点) 图例 线段总条数N
3 3=2+1
4 6=3+2+1
5 10=4+3 +2+1
6 15=5+4 +3+2+1
解答下列问题:
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系
(2)根据上述关系解决如下实际问题,有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有多少种不同的票价 ②要准备多少种车票
【练素养】
17.如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有 个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有 个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有 个交点.(用含n的式子表示)
参考答案
练基础
1.B 2.A
3.没有 1 度量
4.10
5.B 6.C
7.两点确定一条直线
8.【解析】经过两点有且只有一条直线.
9.C
10.【解析】(1)
(2)
(3)
(4)
练能力
11.B 12.C 13.A
14.6 3
15.【解析】(1)如图所示.
(2)如图所示.
(3)如图所示.
16.【解析】(1)N=1+2+3+…+(n-1)
=n(n-1).
(2)①A,B两地之间有三个站点,说明在这条线段上有5个点,则共有10条线段,即有10种票价;②由于从A到B和从B到A的车票不同,则要准备10×2=20种车票.
练素养
17.【解析】3;6;n(n-1).
提示:通过作图发现:3条直线最多有交点1+2=3(个);4条直线最多有交点1+2+3=6(个);5条直线最多有交点1+2+3+4=10(个);…;n条直线最多有交点1+2+3+…+(n-1)=n(n-1)(个).
2
【练基础】
必备知识1 直线、射线、线段
1.射线OA,射线OB表示同一条射线,下面正确的是 ( )
2.如图,下列说法正确的是 ( )
A.直线AB与直线BC是同一条直线
B.线段AB与线段BA是不同的两条线段
C.射线AB与射线AC是两条不同的射线
D.射线BC与射线BA是同一条射线
3.直线、射线、线段没有粗细之分.直线 端点,向两边无限延伸;射线有 个端点,向一边无限延伸;线段有两个端点,所以线段可以 .
4.如图,在线段AB上任取D,E,C三个点,则这个图中共有 条线段.
必备知识2 两点确定一条直线
5.下列现象中,不能用基本事实“两点确定一条直线”来解释的现象是 ( )
A.用两个钉子就可以把木条固定在墙上
B.把弯曲的公路改直,就能缩短路程
C.锯木料时,一般先在木板上画两点,然后过这两点弹出一条墨迹
D.植树时,只要定出两棵树的位置就能确定同一行树所在的直线
6.经过任意三点中的两点共可以画出 ( )
A.一条直线 B.两条直线
C.一条或三条直线 D.三条直线
7.要在墙上钉一根木条,使它不能转动,则至少需要2个钉子,主要依据是 .
8.木工检验木条的边线是否是直的,常常用眼睛从木条的一端向另一端望去,如果看到两个端点及这条边线中的各点都重合于一点,那么这条边线就是直的,说一说其中的道理.
必备知识3 点与线、线与线的位置关系
9.下列说法中,错误的是 ( )
A.经过一点的直线有无数条
B.经过两点的直线只有一条
C.一条直线上只有两个点
D.两条直线相交,只有一个交点
10.按下列语句画出图形.
(1)直线l经过A,B,C三点,点C在点A与点B之间.
(2)经过点O的三条直线a,b,c.
(3)两条直线AB与CD相交于点P.
(4)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q.
【练能力】
11.下列说法中错误的是 ( )
A.过一点可以作无数条直线
B.过已知三点可以画一条直线
C.一条直线通过无数个点
D.两点确定一条直线
12.【保定期末】《红楼梦》第57回有这么一句话,“自古道:‘千里姻缘一线牵’,管姻缘的有一位月下老儿,预先注定,暗里只用一根红线,把这两个人的脚绊住.”请问,这里所说的“线”若是真的,则在数学中指的应是 ( )
A.直线 B.射线
C.线段 D.以上都不对
13.【教材P130习题4.2T12变式】观察下列图形,并阅读相关文字,那么20条直线相交,交点最多有 ( )
A.190个 B.210个
C.380个 D.420个
14.如图,C为直线AB外一点,作射线AC,连接BC,则图中的射线有 条,其中能用图中给出的字母表示出来的射线有 条.
15.【教材P129习题4.2T2变式】如图,已知平面上有四个点A,B,C,D.
(1)连接AB.
(2)画射线AD,线段AC.
(3)画直线BC,与射线AD交于点E.
16.阅读下表:
线段AB上的点数 n(包括A,B两点) 图例 线段总条数N
3 3=2+1
4 6=3+2+1
5 10=4+3 +2+1
6 15=5+4 +3+2+1
解答下列问题:
(1)根据表中规律猜测线段总数N与线段上的点数n(包括线段两个端点)有什么关系
(2)根据上述关系解决如下实际问题,有一辆客车往返于A,B两地,中途停靠三个站点,如果任意两站间的票价都不同,问:①有多少种不同的票价 ②要准备多少种车票
【练素养】
17.如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有 个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有 个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有 个交点.(用含n的式子表示)
参考答案
练基础
1.B 2.A
3.没有 1 度量
4.10
5.B 6.C
7.两点确定一条直线
8.【解析】经过两点有且只有一条直线.
9.C
10.【解析】(1)
(2)
(3)
(4)
练能力
11.B 12.C 13.A
14.6 3
15.【解析】(1)如图所示.
(2)如图所示.
(3)如图所示.
16.【解析】(1)N=1+2+3+…+(n-1)
=n(n-1).
(2)①A,B两地之间有三个站点,说明在这条线段上有5个点,则共有10条线段,即有10种票价;②由于从A到B和从B到A的车票不同,则要准备10×2=20种车票.
练素养
17.【解析】3;6;n(n-1).
提示:通过作图发现:3条直线最多有交点1+2=3(个);4条直线最多有交点1+2+3=6(个);5条直线最多有交点1+2+3+4=10(个);…;n条直线最多有交点1+2+3+…+(n-1)=n(n-1)(个).
2
