2023-2024学年数学人教版七年级上册 课时提高练 4.3.2 角的比较与运算(含答案)
文档属性
| 名称 | 2023-2024学年数学人教版七年级上册 课时提高练 4.3.2 角的比较与运算(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览


文档简介
4.3.2 角的比较与运算
【练基础】
必备知识1 角的比较
1.如图,用三角板比较∠A与∠B的大小,其中正确的是 ( )
A.∠A>∠B
B.∠A<∠B
C.∠A=∠B
D.没有量角器,无法确定
2.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是 ( )
A.∠3>∠4 B.∠3=∠4
C.∠3<∠4 D.不确定
3.【太原期末】如图所示的网格是正方形网格,则∠AOB与∠MPN的关系是 ( )
A.∠AOB>∠MPN B.∠AOB<∠MPN
C.∠AOB=∠MPN D.∠AOB=2∠MPN
4.若∠1=∠2,∠2=∠3,则∠1 ∠3;若∠1>∠2,∠2>∠3,则∠1 ∠3.
必备知识2 角的和与差
5.两个锐角的和 ( )
A.一定是锐角 B.一定是直角
C.一定是钝角 D.可能是锐角
6.【莆田期末】如图,这是一副直角三角板,用它们可以画出一些特殊角,下列角中,不能用这副三角板画出的是 ( )
A.75° B.135°
C.150° D.25°
必备知识3 角平分线
7.如图,已知OC是∠AOB内的一条射线,下列条件中不能确定OC是∠AOB的平分线的是 ( )
A.∠AOC=∠BOC
B.∠AOB=2∠AOC
C.∠AOC+∠COB=∠AOB
D.∠BOC=∠AOB
8.【邢台期末】如图,∠AOB=20°,∠BOC=80°,OE是∠AOC的平分线,则∠COE的度数为 ( )
A.50° B.40° C.30° D.20°
9.【教材P140习题4.3T9变式】把三角尺ABC与BDE按如图所示的方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为 .
【练能力】
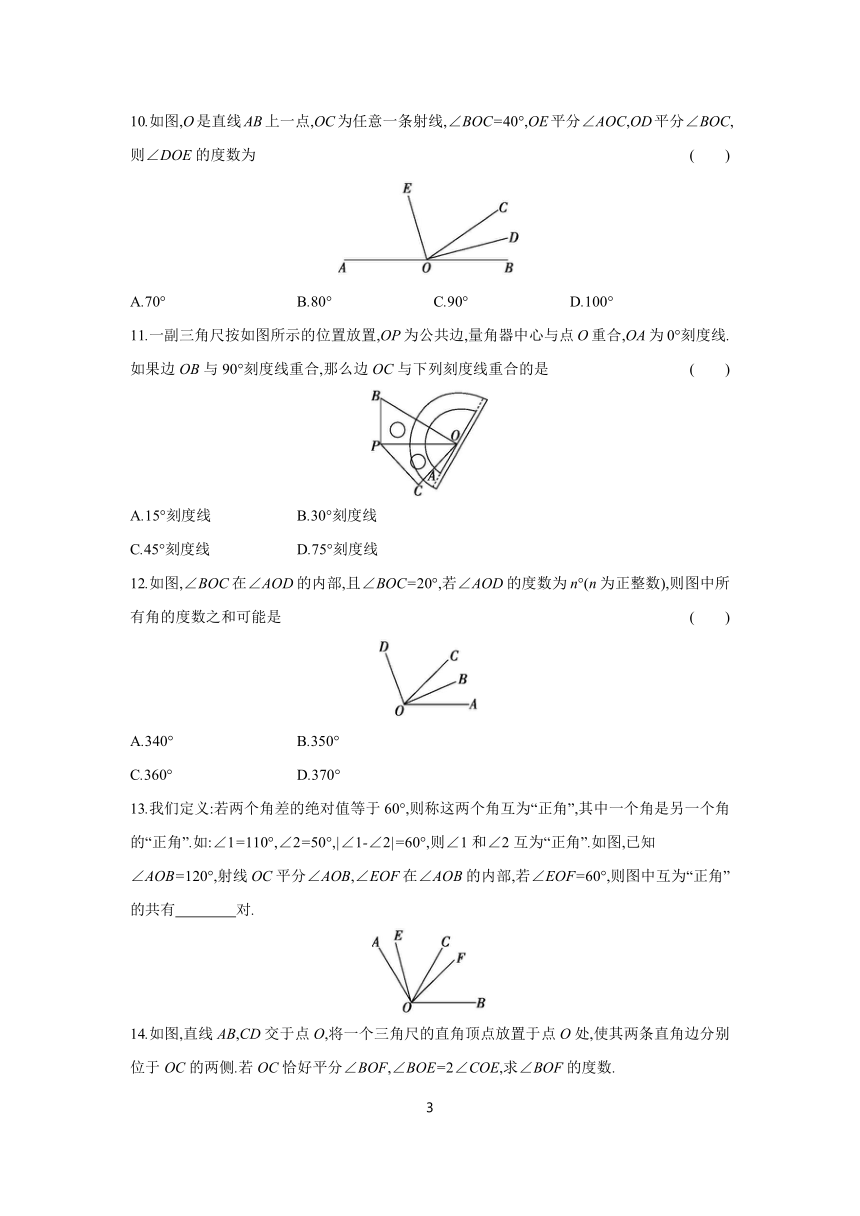
10.如图,O是直线AB上一点,OC为任意一条射线,∠BOC=40°,OE平分∠AOC,OD平分∠BOC,则∠DOE的度数为 ( )
A.70° B.80° C.90° D.100°
11.一副三角尺按如图所示的位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果边OB与90°刻度线重合,那么边OC与下列刻度线重合的是 ( )
A.15°刻度线 B.30°刻度线
C.45°刻度线 D.75°刻度线
12.如图,∠BOC在∠AOD的内部,且∠BOC=20°,若∠AOD的度数为n°(n为正整数),则图中所有角的度数之和可能是 ( )
A.340° B.350°
C.360° D.370°
13.我们定义:若两个角差的绝对值等于60°,则称这两个角互为“正角”,其中一个角是另一个角的“正角”.如:∠1=110°,∠2=50°,|∠1-∠2|=60°,则∠1和∠2互为“正角”.如图,已知∠AOB=120°,射线OC平分∠AOB,∠EOF在∠AOB的内部,若∠EOF=60°,则图中互为“正角”的共有 对.
14.如图,直线AB,CD交于点O,将一个三角尺的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC恰好平分∠BOF,∠BOE=2∠COE,求∠BOF的度数.
【练素养】
15.如图,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数.
(2)若(1)中的∠AOB=α,其他条件不变,求∠MON的度数.
(3)若(1)中的∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.
(4)综合(1)(2)(3)的结果,你能得出什么结论
参考答案
练基础
1.B 2.B 3.C
4.= >
5.D 6.D
7.C 8.A
9.67.5°
练能力
10.C 11.A 12.B
13.7 【解析】因为∠AOB=120°,射线OC平分∠AOB,所以∠AOC=∠BOC=∠AOB=60°,所以∠AOB-∠AOC=60°,∠AOB-∠BOC=60°,又∠EOF=60°,所以∠AOB-∠EOF=60°.因为∠EOF=∠AOC=∠BOC=60°,所以∠AOF-∠AOE=60°,
∠AOF-∠COF=60°,∠BOE-∠EOC=60°,∠BOE-∠BOF=60°,所以题图中互为“正角”的共有∠AOB与∠AOC,∠AOB与∠BOC,∠AOB与∠EOF,∠AOF与∠AOE,∠AOF与∠COF,∠BOE与∠EOC,∠BOE与∠BOF,共7对.
14.【解析】设∠COE=x,则∠BOE=2x,则∠BOC=∠BOE+∠COE=3x.
因为OC平分∠BOF,所以∠BOF=2∠BOC=6x.
因为∠BOF-∠BOE=∠EOF=90°,
所以6x-2x=90°,所以x=22.5°,
所以∠BOF=6x=135°.
练素养
15.【解析】(1)因为∠AOB=90°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
因为OM平分∠AOC,
所以∠MOC=∠AOC=×120°=60°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=×30°=15°,
所以∠MON=∠MOC-∠NOC=60°-15°=45°.
(2)因为∠AOB=α,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=α+30°.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(α+30°)=α+15°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=×30°=15°.
所以∠MON=∠MOC-∠NOC=α+15°-15°=α.
(3)因为∠AOB=90°,∠BOC=β,
所以∠AOC=∠AOB+∠BOC=90°+β.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(90°+β)=45°+β.
因为ON平分∠BOC,
所以∠NOC=∠BOC=β,
所以∠MON=∠MOC-∠NOC=45°+β-β=45°.
(4)∠MON的大小始终等于∠AOB的一半,与∠BOC的大小没有关系.
理由:设∠AOB=α,∠BOC=β,
所以∠AOC=∠AOB+∠BOC=α+β.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(α+β).
因为ON平分∠BOC,
所以∠NOC=∠BOC=,
所以∠MON=∠MOC-∠NOC=(α+β)-==∠AOB.
2
【练基础】
必备知识1 角的比较
1.如图,用三角板比较∠A与∠B的大小,其中正确的是 ( )
A.∠A>∠B
B.∠A<∠B
C.∠A=∠B
D.没有量角器,无法确定
2.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是 ( )
A.∠3>∠4 B.∠3=∠4
C.∠3<∠4 D.不确定
3.【太原期末】如图所示的网格是正方形网格,则∠AOB与∠MPN的关系是 ( )
A.∠AOB>∠MPN B.∠AOB<∠MPN
C.∠AOB=∠MPN D.∠AOB=2∠MPN
4.若∠1=∠2,∠2=∠3,则∠1 ∠3;若∠1>∠2,∠2>∠3,则∠1 ∠3.
必备知识2 角的和与差
5.两个锐角的和 ( )
A.一定是锐角 B.一定是直角
C.一定是钝角 D.可能是锐角
6.【莆田期末】如图,这是一副直角三角板,用它们可以画出一些特殊角,下列角中,不能用这副三角板画出的是 ( )
A.75° B.135°
C.150° D.25°
必备知识3 角平分线
7.如图,已知OC是∠AOB内的一条射线,下列条件中不能确定OC是∠AOB的平分线的是 ( )
A.∠AOC=∠BOC
B.∠AOB=2∠AOC
C.∠AOC+∠COB=∠AOB
D.∠BOC=∠AOB
8.【邢台期末】如图,∠AOB=20°,∠BOC=80°,OE是∠AOC的平分线,则∠COE的度数为 ( )
A.50° B.40° C.30° D.20°
9.【教材P140习题4.3T9变式】把三角尺ABC与BDE按如图所示的方式拼在一起,其中A,B,D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数为 .
【练能力】
10.如图,O是直线AB上一点,OC为任意一条射线,∠BOC=40°,OE平分∠AOC,OD平分∠BOC,则∠DOE的度数为 ( )
A.70° B.80° C.90° D.100°
11.一副三角尺按如图所示的位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果边OB与90°刻度线重合,那么边OC与下列刻度线重合的是 ( )
A.15°刻度线 B.30°刻度线
C.45°刻度线 D.75°刻度线
12.如图,∠BOC在∠AOD的内部,且∠BOC=20°,若∠AOD的度数为n°(n为正整数),则图中所有角的度数之和可能是 ( )
A.340° B.350°
C.360° D.370°
13.我们定义:若两个角差的绝对值等于60°,则称这两个角互为“正角”,其中一个角是另一个角的“正角”.如:∠1=110°,∠2=50°,|∠1-∠2|=60°,则∠1和∠2互为“正角”.如图,已知∠AOB=120°,射线OC平分∠AOB,∠EOF在∠AOB的内部,若∠EOF=60°,则图中互为“正角”的共有 对.
14.如图,直线AB,CD交于点O,将一个三角尺的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC恰好平分∠BOF,∠BOE=2∠COE,求∠BOF的度数.
【练素养】
15.如图,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数.
(2)若(1)中的∠AOB=α,其他条件不变,求∠MON的度数.
(3)若(1)中的∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.
(4)综合(1)(2)(3)的结果,你能得出什么结论
参考答案
练基础
1.B 2.B 3.C
4.= >
5.D 6.D
7.C 8.A
9.67.5°
练能力
10.C 11.A 12.B
13.7 【解析】因为∠AOB=120°,射线OC平分∠AOB,所以∠AOC=∠BOC=∠AOB=60°,所以∠AOB-∠AOC=60°,∠AOB-∠BOC=60°,又∠EOF=60°,所以∠AOB-∠EOF=60°.因为∠EOF=∠AOC=∠BOC=60°,所以∠AOF-∠AOE=60°,
∠AOF-∠COF=60°,∠BOE-∠EOC=60°,∠BOE-∠BOF=60°,所以题图中互为“正角”的共有∠AOB与∠AOC,∠AOB与∠BOC,∠AOB与∠EOF,∠AOF与∠AOE,∠AOF与∠COF,∠BOE与∠EOC,∠BOE与∠BOF,共7对.
14.【解析】设∠COE=x,则∠BOE=2x,则∠BOC=∠BOE+∠COE=3x.
因为OC平分∠BOF,所以∠BOF=2∠BOC=6x.
因为∠BOF-∠BOE=∠EOF=90°,
所以6x-2x=90°,所以x=22.5°,
所以∠BOF=6x=135°.
练素养
15.【解析】(1)因为∠AOB=90°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
因为OM平分∠AOC,
所以∠MOC=∠AOC=×120°=60°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=×30°=15°,
所以∠MON=∠MOC-∠NOC=60°-15°=45°.
(2)因为∠AOB=α,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=α+30°.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(α+30°)=α+15°.
因为ON平分∠BOC,
所以∠NOC=∠BOC=×30°=15°.
所以∠MON=∠MOC-∠NOC=α+15°-15°=α.
(3)因为∠AOB=90°,∠BOC=β,
所以∠AOC=∠AOB+∠BOC=90°+β.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(90°+β)=45°+β.
因为ON平分∠BOC,
所以∠NOC=∠BOC=β,
所以∠MON=∠MOC-∠NOC=45°+β-β=45°.
(4)∠MON的大小始终等于∠AOB的一半,与∠BOC的大小没有关系.
理由:设∠AOB=α,∠BOC=β,
所以∠AOC=∠AOB+∠BOC=α+β.
因为OM平分∠AOC,
所以∠MOC=∠AOC=(α+β).
因为ON平分∠BOC,
所以∠NOC=∠BOC=,
所以∠MON=∠MOC-∠NOC=(α+β)-==∠AOB.
2
