2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:2.4 线段的垂直平分线
文档属性
| 名称 | 2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:2.4 线段的垂直平分线 |

|
|
| 格式 | zip | ||
| 文件大小 | 45.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览


文档简介
课题 2.4 线段的垂直平分线(第1课时) 课型 新授
内容 八上教科书45---47页 主备人 王存如
学习目标 1、经历“线段垂直平分线”概念的形成过程;2、会用尺规作出已知线段的垂直平分线;3、探索线段的垂直平分线的性质,能利用它解决几何问题。
重点 线段的垂直平分线的性质
难点 用尺规画线段的垂直平分线。
学前预习案
独立阅读45---47页的内容,约6分钟, ( http: / / www.21cnjy.com )要求:问题:你对线段有哪些认识 是轴对称图形吗?理由_____________________.操作:1、在一张薄纸上任意画一条线段AB ( http: / / www.21cnjy.com ),折纸,使两个端点A与B重合,你将发现_____________________________________.2 、在折痕上任意取一点P,连接PA、PB,再沿原折痕重新折叠,你又发现________________________________________________.(请与同学交流)
课堂学习案
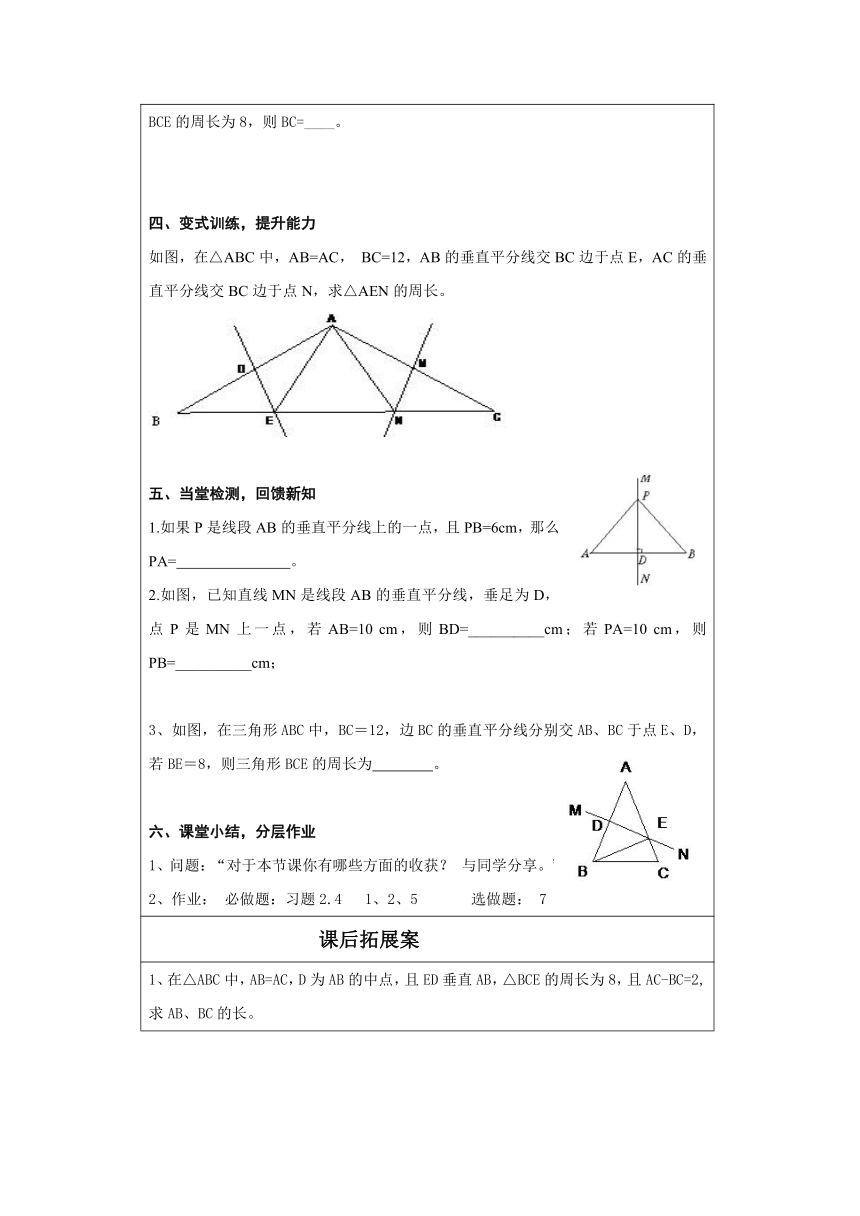
一、创设情境,导入新课某地准备建一所希望小学,要求希望小学的位置到三个村庄A、B、C的距离相等,你能帮助村民确定小学的具体位置吗? 二、自主探究,归纳新知活动一 线段垂直平分线的定义及对称性。学习完成第45页的“实验与探究(1)”。交流互动:(1)将纸展开铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O,线段AO与线段BO的长度有什么关系?(2)直线MN与线段AB有怎样的位置关系?(3)线段AB是轴对称图形吗?小结:直线MN垂直于线段AB,并且平分线段AB,我们把直线MN叫做线段AB的______。线段是轴对称图形,它的一条对称轴是这条线段的________。温馨提示:线段的垂直平分线是一条直线,而且仅有一条;满足两个条件①垂直于这条线段②平分这条线段。活动二 线段的垂直平分线的性质。学习完成第46页的“实验与探究(2)”。操作、实践:(1)如图,折纸使A、B重合,你发现了什么?(折痕就是对称轴)(2)在折痕上找一点M,MA与MB的大小有什么关系?说说理由,小组交流总结。性质:_____________________________。温馨提示:此性质是证明两线段相等的常用方法之一。活动三 用尺规画线段的垂直平分线。自学课本作图,小组交流,完成以下问题。已知:线段AB 求作:线段AB的垂直平分线作法:1、分别以点A与点B为 ,以 为半径画弧,两弧分别相交于点M、N;2、过M、N两点作 。结论: 温馨提示:做图时不要擦去痕迹,要注意体现射线的特征。三、应用练习,巩固性质1、Rt△ABC中,∠C=90o,AC的垂直平分线交AB于D,若AD=2,则BD=_____。2、在Rt△ABC中,∠C=90o,∠B= ( http: / / www.21cnjy.com )60 o,BC的垂直平分线交斜边AB于D,交BC于E,连结CD,则其中等于60o的角有______个。3、如图所示,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于M,∠A=40o,求∠NMB的大小。4、如图,ED为△ABC的AC边的中垂线,且AB=5,△BCE的周长为8,则BC=____。四、变式训练,提升能力如图,在△ABC中,AB=AC, BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求△AEN的周长。 ( http: / / www.21cnjy.com )五、当堂检测,回馈新知1.如果P是线段AB的垂直平分线上的一点,且PB=6cm,那么PA= 。2.如图,已知直线MN是线 ( http: / / www.21cnjy.com )段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;3、如图,在三角形ABC中,BC=12,边BC的垂直平分线分别交AB、BC于点E、D,若BE=8,则三角形BCE的周长为 。六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.4 1、2、5 选做题: 7
课后拓展案
1、在△ABC中,AB=AC,D为AB的中点,且ED垂直AB,△BCE的周长为8,且AC-BC=2,求AB、BC的长。 ( http: / / www.21cnjy.com )2、已知线段AB,用尺规作出它的三个四等分点。(写出作图步骤,并作出图形)
课题 2.4线段的垂直平分线(第2课时) 课型 新授
内容 八上教科书48---50页 主备人 王存如
学习目标 1、掌握基本作图:过一点作一条直线的垂线;2、会用基本作图解决现实问题。
重点 线段垂直平分线的尺规作图
难点 会用基本作图解决现实问题。
学前预习案
独立阅读48---50页的内容,约6分钟,要求:思考:在课本45页“实验与探究”(1)(2)中的两个作图与“作一条线段的垂直平分线”有什么关系?其中蕴含什么数学思想?2、体会例题2的理论依据是什么?
课堂学习案
一、创设情境,导入新课直线AB表示一条小河,一牧民在C处放马,现在要到河边去饮马,然后回到帐篷点D处(C、D在小河同旁)。问在何处饮马,才能使他所走路程最短?二、自主探究,归纳新知学习课本48页中的“实验与探究”,归纳:(1)已知直线l和l上一点P,怎样过点P作直线l的垂线?(2)已知直线l和l外一点P,怎样过点P作直线l的垂线?(小组讨论交流,理解并熟记作法)(3)体会在解决“过一点作已知直线的垂线”这一问题时,运用了哪些基本的数学思想?三、应用练习,巩固性质课本中练习1、2四、变式训练,提升能力课本50页中的“挑战自我”。五、当堂检测,回馈新知1、过点P作直线l的垂线和斜线,叙述正确的是( )A、都能作且只能作一条 B、垂线能作且只能作一条,斜线可作无数条C、垂线能作两条,斜线可作无数条 D、均可作无数条2、经过一点可以作并且只能作已知直线的一条( ) A、垂线 B、垂线段 C、平行线 D、以上都可以六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.1 6 选做题:8
课后拓展案
课本中习题2.4 3课本中习题2.4 4小河边有两个村庄A村和B村,现要在河边建一自来水厂分别向A村和B村供水。若要使自来水厂到A村和B村的距离相等,应建在什么地方?若要使自来水厂到A村和B村的水管最省料,应建在什么地方 (保留作图痕迹,不写作法)
B.
C.
A.
C D
B
A
A B
内容 八上教科书45---47页 主备人 王存如
学习目标 1、经历“线段垂直平分线”概念的形成过程;2、会用尺规作出已知线段的垂直平分线;3、探索线段的垂直平分线的性质,能利用它解决几何问题。
重点 线段的垂直平分线的性质
难点 用尺规画线段的垂直平分线。
学前预习案
独立阅读45---47页的内容,约6分钟, ( http: / / www.21cnjy.com )要求:问题:你对线段有哪些认识 是轴对称图形吗?理由_____________________.操作:1、在一张薄纸上任意画一条线段AB ( http: / / www.21cnjy.com ),折纸,使两个端点A与B重合,你将发现_____________________________________.2 、在折痕上任意取一点P,连接PA、PB,再沿原折痕重新折叠,你又发现________________________________________________.(请与同学交流)
课堂学习案
一、创设情境,导入新课某地准备建一所希望小学,要求希望小学的位置到三个村庄A、B、C的距离相等,你能帮助村民确定小学的具体位置吗? 二、自主探究,归纳新知活动一 线段垂直平分线的定义及对称性。学习完成第45页的“实验与探究(1)”。交流互动:(1)将纸展开铺平,记折痕所在的直线为MN,直线MN与线段AB的交点为O,线段AO与线段BO的长度有什么关系?(2)直线MN与线段AB有怎样的位置关系?(3)线段AB是轴对称图形吗?小结:直线MN垂直于线段AB,并且平分线段AB,我们把直线MN叫做线段AB的______。线段是轴对称图形,它的一条对称轴是这条线段的________。温馨提示:线段的垂直平分线是一条直线,而且仅有一条;满足两个条件①垂直于这条线段②平分这条线段。活动二 线段的垂直平分线的性质。学习完成第46页的“实验与探究(2)”。操作、实践:(1)如图,折纸使A、B重合,你发现了什么?(折痕就是对称轴)(2)在折痕上找一点M,MA与MB的大小有什么关系?说说理由,小组交流总结。性质:_____________________________。温馨提示:此性质是证明两线段相等的常用方法之一。活动三 用尺规画线段的垂直平分线。自学课本作图,小组交流,完成以下问题。已知:线段AB 求作:线段AB的垂直平分线作法:1、分别以点A与点B为 ,以 为半径画弧,两弧分别相交于点M、N;2、过M、N两点作 。结论: 温馨提示:做图时不要擦去痕迹,要注意体现射线的特征。三、应用练习,巩固性质1、Rt△ABC中,∠C=90o,AC的垂直平分线交AB于D,若AD=2,则BD=_____。2、在Rt△ABC中,∠C=90o,∠B= ( http: / / www.21cnjy.com )60 o,BC的垂直平分线交斜边AB于D,交BC于E,连结CD,则其中等于60o的角有______个。3、如图所示,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于M,∠A=40o,求∠NMB的大小。4、如图,ED为△ABC的AC边的中垂线,且AB=5,△BCE的周长为8,则BC=____。四、变式训练,提升能力如图,在△ABC中,AB=AC, BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求△AEN的周长。 ( http: / / www.21cnjy.com )五、当堂检测,回馈新知1.如果P是线段AB的垂直平分线上的一点,且PB=6cm,那么PA= 。2.如图,已知直线MN是线 ( http: / / www.21cnjy.com )段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10 cm,则BD=__________cm;若PA=10 cm,则PB=__________cm;3、如图,在三角形ABC中,BC=12,边BC的垂直平分线分别交AB、BC于点E、D,若BE=8,则三角形BCE的周长为 。六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.4 1、2、5 选做题: 7
课后拓展案
1、在△ABC中,AB=AC,D为AB的中点,且ED垂直AB,△BCE的周长为8,且AC-BC=2,求AB、BC的长。 ( http: / / www.21cnjy.com )2、已知线段AB,用尺规作出它的三个四等分点。(写出作图步骤,并作出图形)
课题 2.4线段的垂直平分线(第2课时) 课型 新授
内容 八上教科书48---50页 主备人 王存如
学习目标 1、掌握基本作图:过一点作一条直线的垂线;2、会用基本作图解决现实问题。
重点 线段垂直平分线的尺规作图
难点 会用基本作图解决现实问题。
学前预习案
独立阅读48---50页的内容,约6分钟,要求:思考:在课本45页“实验与探究”(1)(2)中的两个作图与“作一条线段的垂直平分线”有什么关系?其中蕴含什么数学思想?2、体会例题2的理论依据是什么?
课堂学习案
一、创设情境,导入新课直线AB表示一条小河,一牧民在C处放马,现在要到河边去饮马,然后回到帐篷点D处(C、D在小河同旁)。问在何处饮马,才能使他所走路程最短?二、自主探究,归纳新知学习课本48页中的“实验与探究”,归纳:(1)已知直线l和l上一点P,怎样过点P作直线l的垂线?(2)已知直线l和l外一点P,怎样过点P作直线l的垂线?(小组讨论交流,理解并熟记作法)(3)体会在解决“过一点作已知直线的垂线”这一问题时,运用了哪些基本的数学思想?三、应用练习,巩固性质课本中练习1、2四、变式训练,提升能力课本50页中的“挑战自我”。五、当堂检测,回馈新知1、过点P作直线l的垂线和斜线,叙述正确的是( )A、都能作且只能作一条 B、垂线能作且只能作一条,斜线可作无数条C、垂线能作两条,斜线可作无数条 D、均可作无数条2、经过一点可以作并且只能作已知直线的一条( ) A、垂线 B、垂线段 C、平行线 D、以上都可以六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.1 6 选做题:8
课后拓展案
课本中习题2.4 3课本中习题2.4 4小河边有两个村庄A村和B村,现要在河边建一自来水厂分别向A村和B村供水。若要使自来水厂到A村和B村的距离相等,应建在什么地方?若要使自来水厂到A村和B村的水管最省料,应建在什么地方 (保留作图痕迹,不写作法)
B.
C.
A.
C D
B
A
A B
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
