沪教版九年级数学上册教案:24-1.2相似形与比例线段2
文档属性
| 名称 | 沪教版九年级数学上册教案:24-1.2相似形与比例线段2 |

|
|
| 格式 | zip | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 21:15:08 | ||
图片预览


文档简介
课 题 相似形与比例线段
教学目标 三角形一边的平行线的性质定理三角形一边的平行线的性质定理的推论
重点、难点 重点:三角形一边的平行线的性质定理 难点:三角形一边的平行线的性质定理
考点及考试要求 熟练掌握三角形一边的平行线的性质定理及推论
教学内容
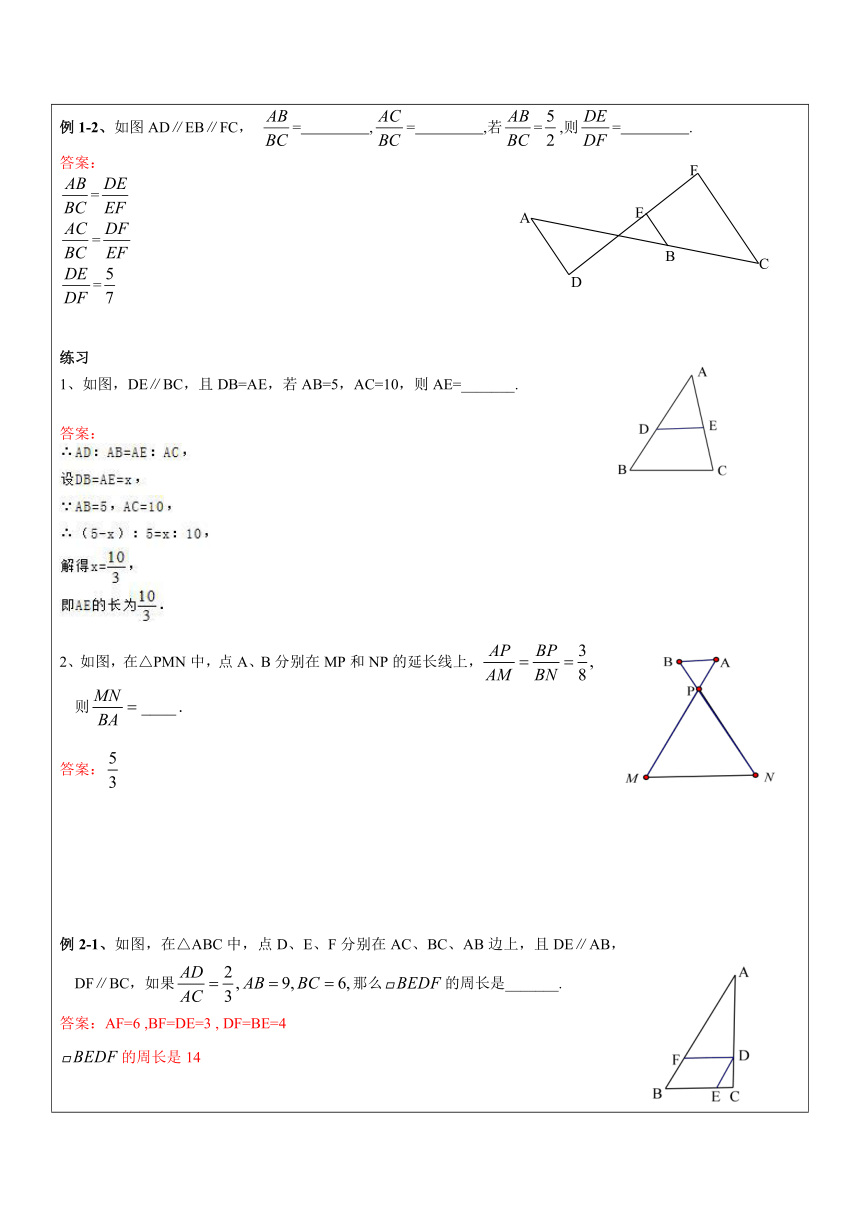
课堂导入知识精讲1、三角形一边的平行线性质定理:平行于三角形一边的直线截其它两边所在的直线,截得的对应线段成比例。如图(1),若DE∥BC,则或或如图(2),若DE∥BC,则或或 ( http: / / www.21cnjy.com )证明:答案:利用比例性质举例说明2、三角形一边的平行线性质定理推论:平行 ( http: / / www.21cnjy.com )于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例。如图(1)已知:△ABC中,点D、E分别在AB、AC上,且DE∥BC,则;如图(2)已知:△ABC中,点D、E分别在CA、BA的延长线上,且DE∥BC,则.证明:答案:利用比例性质举例说明三、典例精析例1-1.如图,在中,DE∥BC,若AD=2,DB=3,则AE:AC= ;若AE:EC=3:5,AB=16,则AD= ;若AE:EC=2:3,DB-AD=3,则AD= 。答案:2:5, 6, 6例1-2、如图AD∥EB∥FC, = ,= ,若=,则= . 答案: ===练习 1、如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE=_______.答案: ( http: / / www.21cnjy.com )2、如图,在△PMN中,点A、B分别在MP和NP的延长线上,则答案:例2-1、如图,在△ABC中,点D、E、F分别在AC、BC、AB边上,且DE∥AB,DF∥BC,如果那么的周长是_______.答案:AF=6 ,BF=DE=3 , DF=BE=4的周长是14例2-2、如图,在△ABC中,AC=15,AB=10,四边形ADEF为菱形,则CF=_______.答案:设菱形边长为x由题意得:(15-x):15=x:10解得:x=6练习 如图,点D、E分别是AB的三等分点,DF∥EG∥BC,若BC=12,则DF=______.答案:42、已知:如图中,CD是的∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE.答案:由题意得: AD:DB=AC:BC=2:3则BC=∵AD:AB=DE:BC ∴AD:AB=2:5=DE:BC∴所以DE=总结: 四、课堂巩固练习1.已知:如图中,DE∥BC,(1)若AD=3,DB=5,AE=2.25,求EC的长;答案:EC=3.75(2)若AB=5,AD=2,AC=4,求EC;答案:EC=2.4(3)若AE:EC=2:3,DB-AD=3,求AD、DB的长。答案:AD= 6 DB=92、如图,中,DE∥BC,AN交DE于M,求证:。答案:∵,∴3、 已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD,求证:答案:由题意得:BG:BE=BF:BD BE:BA=BD:BC
BE:BA=BF:BD BG:BE=BD:BC五、课后作业1.已知:如图,EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长。答案: ( http: / / www.21cnjy.com )2.已知:如图,四边形AEDF为菱形,AB=12,BC=10,AC=8,求:BD、DC及AF的长。答案:设AF为x.则AF=FD=DE=AE=x.再设BD=y则有 x/8=(12-x)/12=y/10,x=4.8 y=6.
所以CD=4.BD=6,AF=4.83.如图,在△ABC中,点D、E分别在边AC、AB上,如果DE∥BC,求答案:∵DE‖BC,
∴AE:EB=AD:DC
∵SΔADE:SΔEBD=AE:EB,SΔADB:SΔDBC=AD:DC
若设S△EBD=S
则3:S=(3+S):18
S2+3S-54=0
(S+9)(S-6)=0
S1=-9 (舍去) S2=6
所以S△EBD=6
A
B
D
E
C
A
D
E
F
B
C
A
D
B
C
E
A
D
B
C
E
A
B
D
E
C
N
M
A
B
F
D
C
E
G
E
F
B
A
C
D
A
F
B
D
C
E
教学目标 三角形一边的平行线的性质定理三角形一边的平行线的性质定理的推论
重点、难点 重点:三角形一边的平行线的性质定理 难点:三角形一边的平行线的性质定理
考点及考试要求 熟练掌握三角形一边的平行线的性质定理及推论
教学内容
课堂导入知识精讲1、三角形一边的平行线性质定理:平行于三角形一边的直线截其它两边所在的直线,截得的对应线段成比例。如图(1),若DE∥BC,则或或如图(2),若DE∥BC,则或或 ( http: / / www.21cnjy.com )证明:答案:利用比例性质举例说明2、三角形一边的平行线性质定理推论:平行 ( http: / / www.21cnjy.com )于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例。如图(1)已知:△ABC中,点D、E分别在AB、AC上,且DE∥BC,则;如图(2)已知:△ABC中,点D、E分别在CA、BA的延长线上,且DE∥BC,则.证明:答案:利用比例性质举例说明三、典例精析例1-1.如图,在中,DE∥BC,若AD=2,DB=3,则AE:AC= ;若AE:EC=3:5,AB=16,则AD= ;若AE:EC=2:3,DB-AD=3,则AD= 。答案:2:5, 6, 6例1-2、如图AD∥EB∥FC, = ,= ,若=,则= . 答案: ===练习 1、如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE=_______.答案: ( http: / / www.21cnjy.com )2、如图,在△PMN中,点A、B分别在MP和NP的延长线上,则答案:例2-1、如图,在△ABC中,点D、E、F分别在AC、BC、AB边上,且DE∥AB,DF∥BC,如果那么的周长是_______.答案:AF=6 ,BF=DE=3 , DF=BE=4的周长是14例2-2、如图,在△ABC中,AC=15,AB=10,四边形ADEF为菱形,则CF=_______.答案:设菱形边长为x由题意得:(15-x):15=x:10解得:x=6练习 如图,点D、E分别是AB的三等分点,DF∥EG∥BC,若BC=12,则DF=______.答案:42、已知:如图中,CD是的∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE.答案:由题意得: AD:DB=AC:BC=2:3则BC=∵AD:AB=DE:BC ∴AD:AB=2:5=DE:BC∴所以DE=总结: 四、课堂巩固练习1.已知:如图中,DE∥BC,(1)若AD=3,DB=5,AE=2.25,求EC的长;答案:EC=3.75(2)若AB=5,AD=2,AC=4,求EC;答案:EC=2.4(3)若AE:EC=2:3,DB-AD=3,求AD、DB的长。答案:AD= 6 DB=92、如图,中,DE∥BC,AN交DE于M,求证:。答案:∵,∴3、 已知:△ABC中,E、G、D、F分别是边AB、CB上的一点,且GF∥ED∥AC,EF∥AD,求证:答案:由题意得:BG:BE=BF:BD BE:BA=BD:BC
BE:BA=BF:BD BG:BE=BD:BC五、课后作业1.已知:如图,EF⊥FD,AB⊥FD,CD⊥FD,EF=1.5,AB=2.5,FB=2.2,BD=3.6,求CD的长。答案: ( http: / / www.21cnjy.com )2.已知:如图,四边形AEDF为菱形,AB=12,BC=10,AC=8,求:BD、DC及AF的长。答案:设AF为x.则AF=FD=DE=AE=x.再设BD=y则有 x/8=(12-x)/12=y/10,x=4.8 y=6.
所以CD=4.BD=6,AF=4.83.如图,在△ABC中,点D、E分别在边AC、AB上,如果DE∥BC,求答案:∵DE‖BC,
∴AE:EB=AD:DC
∵SΔADE:SΔEBD=AE:EB,SΔADB:SΔDBC=AD:DC
若设S△EBD=S
则3:S=(3+S):18
S2+3S-54=0
(S+9)(S-6)=0
S1=-9 (舍去) S2=6
所以S△EBD=6
A
B
D
E
C
A
D
E
F
B
C
A
D
B
C
E
A
D
B
C
E
A
B
D
E
C
N
M
A
B
F
D
C
E
G
E
F
B
A
C
D
A
F
B
D
C
E
