第2单元 因数与倍数(单元测试)-2023-2024学年五年级下册数学人教版(含答案)
文档属性
| 名称 | 第2单元 因数与倍数(单元测试)-2023-2024学年五年级下册数学人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 63.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 11:28:44 | ||
图片预览

文档简介
第2单元 因数与倍数(单元测试)-2023-2024学年五年级下册数学人教版
一、单选题
1.一个质数( )。
A.没有因数 B.只有一个因数
C.只有2个因数 D.只有3个因数
2.一个数既是16的因数,又是16的倍数,这个数是( )。
A.1 B.16 C.32 D.48
3.两个不同的质数相乘的积一定是( )。
A.质数 B.合数 C.偶数 D.奇数
4.把再加上( )个就是最小的质数。
A.4 B.5 C.6 D.7
5.一种浮萍,每天长大一倍,长到第20天时长满整个河面,它长到河面一半时要用( )。
A.10天 B.5天 C.19天 D.15天
二、判断题
6.自然数中除了质数就是合数。( )
7.任何一个非零自然数的因数至少有两个。( )
8.个位上是0的自然数(0除外)都是2和5的倍数。
9.因为4×6=24,所以4和6都是因数,24是倍数。
10.一个非0自然数的因数的个数是有限的,倍数的个数是无限的。( )
三、填空题
11.素数 两个因数,合数 有3个因数.
12.在1~20中,既是质数又是偶数的数有 ,既是合数又是奇数的数有 , 不是质数也不是合数。
13.一个数既是6的倍数,又是36的因数,这个数可能是 。
14.5×9=45, 和 都是45的因数,45是 的倍数,也是 的倍数。
15.最小的奇数是 ,最小的偶数是 ,最小的质数是 ,最小的合数是 。
16.一个盒子里有400枚棋子,其中黑色和白色的棋子各200枚,我们对这些棋子做如下操作:每次拿出2枚棋子,如果颜色相同,就补1枚黑色棋子回去;如果颜色不同,就补1枚白色的棋子回去.这样的操作,实际上就是每次都少了1枚棋子,那么,经过399次操作后,最后剩下的棋子是 颜色(填黑或者白)
四、解答题
17.有45名学生,把他们分到4个社区参加义务劳动,每个社区参加的人数只能是奇数,这件事能办到吗?为什么?
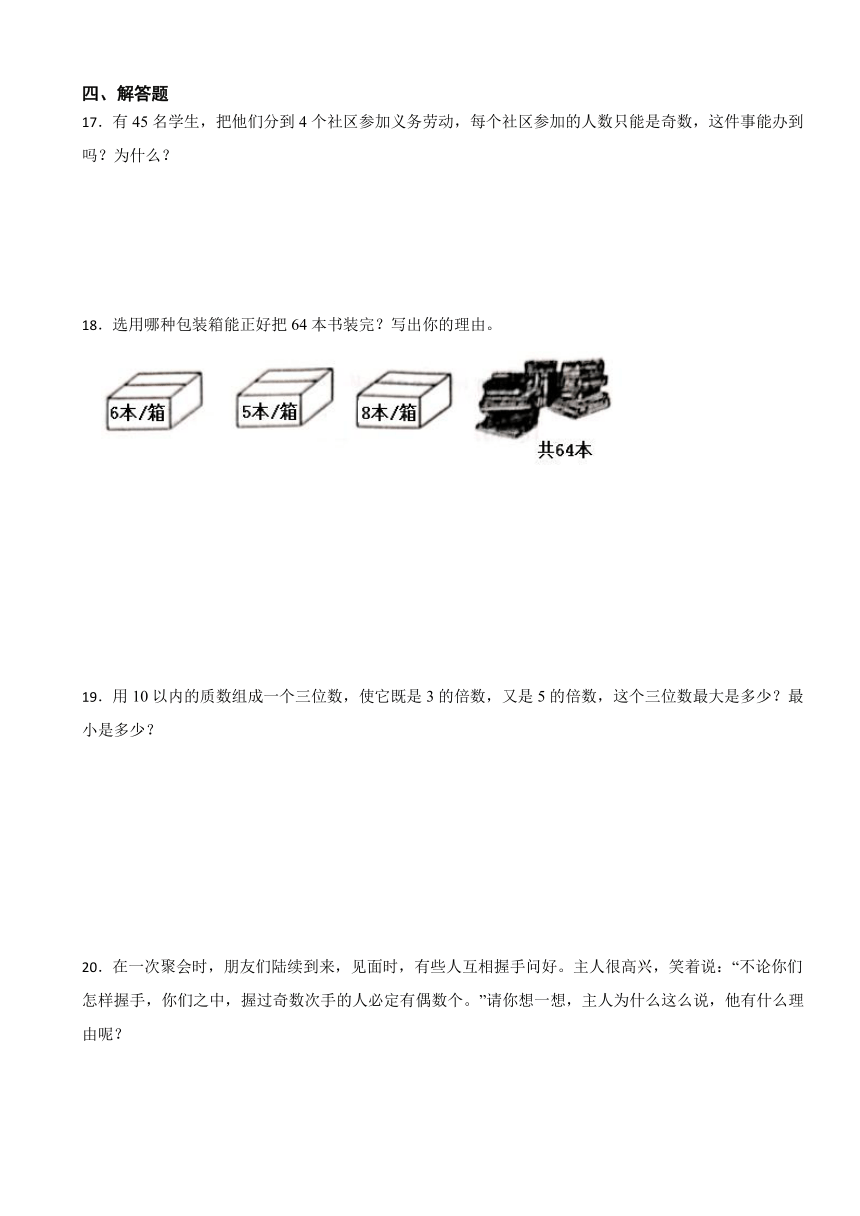
18.选用哪种包装箱能正好把64本书装完?写出你的理由。
19.用10以内的质数组成一个三位数,使它既是3的倍数,又是5的倍数,这个三位数最大是多少?最小是多少?
20.在一次聚会时,朋友们陆续到来,见面时,有些人互相握手问好。主人很高兴,笑着说:“不论你们怎样握手,你们之中,握过奇数次手的人必定有偶数个。”请你想一想,主人为什么这么说,他有什么理由呢?
21.一个两层的书架,上层放的书本数是下层的3倍,如果把上层的书搬120本到下层,那么两层的书本数正好相等,上。下两层原来各有多少本书?
22.五(1)班有48名同学报名参加义务劳动,老师把他们分成人数相等的若干个小组。要求组数大于2个组,小于16个组,有几种分法?每种分法每组多少人?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】错误
7.【答案】错误
8.【答案】正确
9.【答案】错误
10.【答案】正确
11.【答案】只有;至少
12.【答案】2、9;15;1
13.【答案】6、12、18、36
14.【答案】9;5;9;5
15.【答案】1;0;2;4
16.【答案】黑
17.【答案】解:奇数+奇数+奇数+奇数=偶数
45是奇数,不能分成4个奇数的和。
答:不能办到,因为45是奇数,而4个奇数相加的和是偶数,无法把45拆成4个奇数相加的和。
18.【答案】解:64的因数有1、2、4、8、16、32、64,所以选用第三个包装箱。
19.【答案】解:10以内的质数有2、3、5、7;既是3的倍数又是5的倍数,这个数的个位数字一定是5,3+7+5=15,所以这个数是由3、5、7组成的,最大的三位数是753,最小的三位数是375.
答:这个三位数最大是735,最小是375.
20.【答案】解:⑴握偶数次手的人:不管奇数个人还是偶数个人。总次数=偶数次×人数=偶数
⑵ 握奇数次手的总次数=握手总次数-偶数次握手总次数,即偶-偶=偶,而偶=奇数次×人数人数为偶数,由此证明。
21.【答案】解:下册:120本 上层:120×3=360本
答:上册360本,下册120本
22.【答案】解:48=1×48=2×24=3×16=4×12=6×8,
可以分给3组,每组16人,
可以分给4组,每组12人,
可以分给12组,每组4人,
可以分给6组,每组8人,
可以分给8组,每组6人,
答:有5种分法;分给3组,每组16人;分给4组,每组12人;分给12组,每组4人;分给6组,每组8人;分给8组,每组6人。
一、单选题
1.一个质数( )。
A.没有因数 B.只有一个因数
C.只有2个因数 D.只有3个因数
2.一个数既是16的因数,又是16的倍数,这个数是( )。
A.1 B.16 C.32 D.48
3.两个不同的质数相乘的积一定是( )。
A.质数 B.合数 C.偶数 D.奇数
4.把再加上( )个就是最小的质数。
A.4 B.5 C.6 D.7
5.一种浮萍,每天长大一倍,长到第20天时长满整个河面,它长到河面一半时要用( )。
A.10天 B.5天 C.19天 D.15天
二、判断题
6.自然数中除了质数就是合数。( )
7.任何一个非零自然数的因数至少有两个。( )
8.个位上是0的自然数(0除外)都是2和5的倍数。
9.因为4×6=24,所以4和6都是因数,24是倍数。
10.一个非0自然数的因数的个数是有限的,倍数的个数是无限的。( )
三、填空题
11.素数 两个因数,合数 有3个因数.
12.在1~20中,既是质数又是偶数的数有 ,既是合数又是奇数的数有 , 不是质数也不是合数。
13.一个数既是6的倍数,又是36的因数,这个数可能是 。
14.5×9=45, 和 都是45的因数,45是 的倍数,也是 的倍数。
15.最小的奇数是 ,最小的偶数是 ,最小的质数是 ,最小的合数是 。
16.一个盒子里有400枚棋子,其中黑色和白色的棋子各200枚,我们对这些棋子做如下操作:每次拿出2枚棋子,如果颜色相同,就补1枚黑色棋子回去;如果颜色不同,就补1枚白色的棋子回去.这样的操作,实际上就是每次都少了1枚棋子,那么,经过399次操作后,最后剩下的棋子是 颜色(填黑或者白)
四、解答题
17.有45名学生,把他们分到4个社区参加义务劳动,每个社区参加的人数只能是奇数,这件事能办到吗?为什么?
18.选用哪种包装箱能正好把64本书装完?写出你的理由。
19.用10以内的质数组成一个三位数,使它既是3的倍数,又是5的倍数,这个三位数最大是多少?最小是多少?
20.在一次聚会时,朋友们陆续到来,见面时,有些人互相握手问好。主人很高兴,笑着说:“不论你们怎样握手,你们之中,握过奇数次手的人必定有偶数个。”请你想一想,主人为什么这么说,他有什么理由呢?
21.一个两层的书架,上层放的书本数是下层的3倍,如果把上层的书搬120本到下层,那么两层的书本数正好相等,上。下两层原来各有多少本书?
22.五(1)班有48名同学报名参加义务劳动,老师把他们分成人数相等的若干个小组。要求组数大于2个组,小于16个组,有几种分法?每种分法每组多少人?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】错误
7.【答案】错误
8.【答案】正确
9.【答案】错误
10.【答案】正确
11.【答案】只有;至少
12.【答案】2、9;15;1
13.【答案】6、12、18、36
14.【答案】9;5;9;5
15.【答案】1;0;2;4
16.【答案】黑
17.【答案】解:奇数+奇数+奇数+奇数=偶数
45是奇数,不能分成4个奇数的和。
答:不能办到,因为45是奇数,而4个奇数相加的和是偶数,无法把45拆成4个奇数相加的和。
18.【答案】解:64的因数有1、2、4、8、16、32、64,所以选用第三个包装箱。
19.【答案】解:10以内的质数有2、3、5、7;既是3的倍数又是5的倍数,这个数的个位数字一定是5,3+7+5=15,所以这个数是由3、5、7组成的,最大的三位数是753,最小的三位数是375.
答:这个三位数最大是735,最小是375.
20.【答案】解:⑴握偶数次手的人:不管奇数个人还是偶数个人。总次数=偶数次×人数=偶数
⑵ 握奇数次手的总次数=握手总次数-偶数次握手总次数,即偶-偶=偶,而偶=奇数次×人数人数为偶数,由此证明。
21.【答案】解:下册:120本 上层:120×3=360本
答:上册360本,下册120本
22.【答案】解:48=1×48=2×24=3×16=4×12=6×8,
可以分给3组,每组16人,
可以分给4组,每组12人,
可以分给12组,每组4人,
可以分给6组,每组8人,
可以分给8组,每组6人,
答:有5种分法;分给3组,每组16人;分给4组,每组12人;分给12组,每组4人;分给6组,每组8人;分给8组,每组6人。
