人教版八年级下册17.1 勾股定理 课后练习(含答案)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理 课后练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 18:50:22 | ||
图片预览


文档简介
17.1 勾股定理 课后练习
一、单选题(共11小题)
1. 以下列各组线段为边作三角形,不能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
2. 已知一个直角三角形的两边长分别为 和 ,则第三边长的是
A. B. C. D. 或
3. 若 中,,且 ,,则 的值是
A. B. C. D.
4. 如图,已知正方形 的面积为 ,正方形 的面积为 ,则正方形 的面积为
A. B. C. D.
5. 给定下列条件,不能判定三角形是直角三角形的是
A. B.
C. D.
6. 如图, 是直角 斜边 上的高,,图中相等的角共有
A. 对 B. 对 C. 对 D. 对
7. 如图所示,在 中,,, 交 于点 .若 ,则
A. B. C. D.
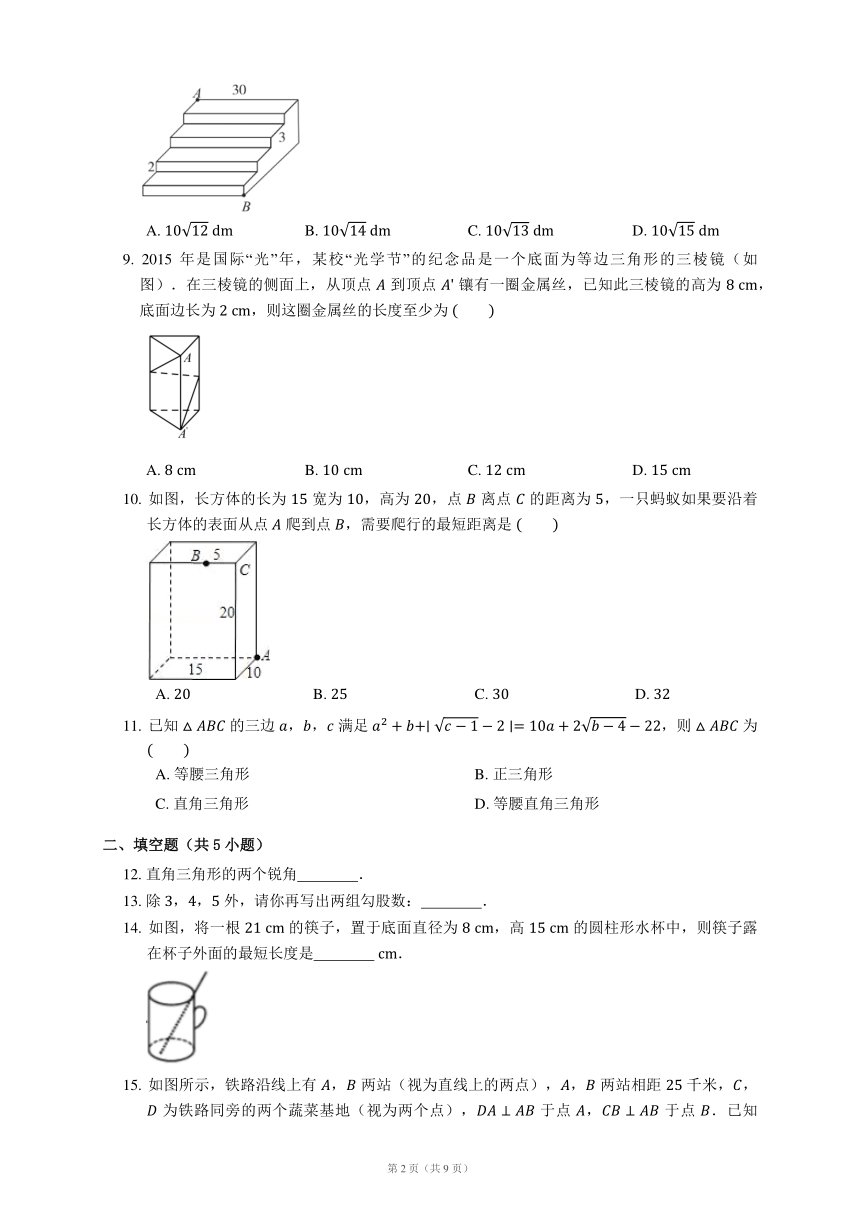
8. 如图是一个四级台阶,它的每一级的长、宽、高分别为 ,,, 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
9. 2015年是国际“光”年,某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点 到顶点 镶有一圈金属丝,已知此三棱镜的高为 ,底面边长为 ,则这圈金属丝的长度至少为
A. B. C. D.
10. 如图,长方体的长为 宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是
A. B. C. D.
11. 已知 的三边 ,, 满足 ,则 为
A. 等腰三角形 B. 正三角形
C. 直角三角形 D. 等腰直角三角形
二、填空题(共5小题)
12. 直角三角形的两个锐角 .
13. 除 ,, 外,请你再写出两组勾股数: .
14. 如图,将一根 的筷子,置于底面直径为 ,高 的圆柱形水杯中,则筷子露在杯子外面的最短长度是 .
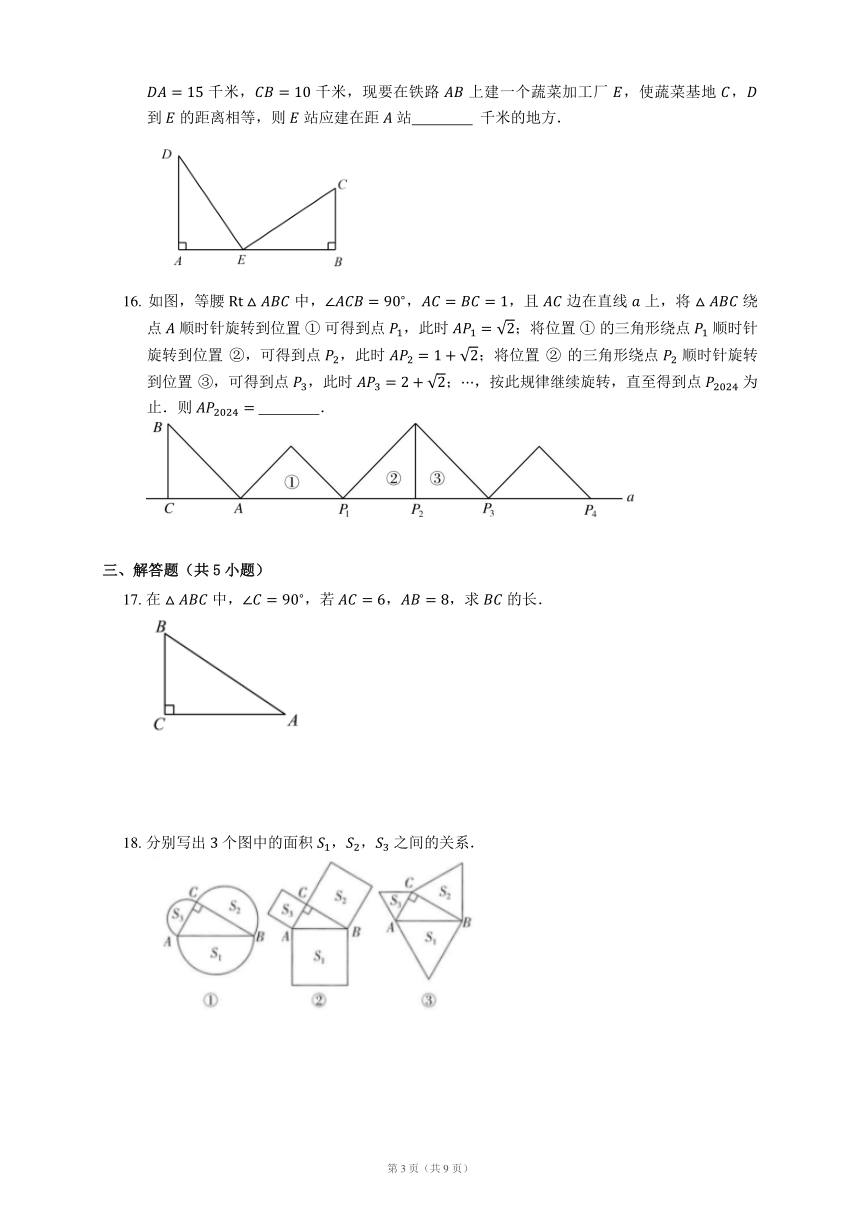
15. 如图所示,铁路沿线上有 , 两站(视为直线上的两点),, 两站相距 千米,, 为铁路同旁的两个蔬菜基地(视为两个点), 于点 , 于点 .已知 千米, 千米,现要在铁路 上建一个蔬菜加工厂 ,使蔬菜基地 , 到 的距离相等,则 站应建在距 站 千米的地方.
16. 如图,等腰 中,,,且 边在直线 上,将 绕点 顺时针旋转到位置 ① 可得到点 ,此时 ;将位置 ① 的三角形绕点 顺时针旋转到位置 ②,可得到点 ,此时 ;将位置 ② 的三角形绕点 顺时针旋转到位置 ③,可得到点 ,此时 ;,按此规律继续旋转,直至得到点 为止.则 .
三、解答题(共5小题)
17. 在 中,,若 ,,求 的长.
18. 分别写出 个图中的面积 ,, 之间的关系.
19. 一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
20. 如图①,圆柱的底面半径为 ,圆柱高 为 , 是底面直径,求一只蚂蚁从点 出发沿圆柱表面爬行到点 的最短路线,小明设计了两条路线:
路线 :高线 底面直径 ,如图①所示,设长度为 .
路线 :侧面展开图中的线段 ,如图②所示,设长度为 .
请按照小明的思路补充下面解题过程:
(1)解:,
;
.
(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为 ,高 为 ”继续按前面的路线进行计算.(结果保留 )
①此时,路线 ;
路线 .
②选择哪条路线较短 试说明理由.
21. 叶老师在与学生进行“蚂蚁怎样爬路程最短”的课题研究时,设计了以下两个问题.请你根据下面所给的重要条件分别求出蚂蚁需要爬行的最短路程(结果保留根号).
(1)如图①,正方体的棱长为 ,一只蚂蚁欲从正方体底面上的点 处沿着正方体表面爬到点 处;
(2)如图②,长方体的长和宽都为 ,高为 ,一只蚂蚁欲从长方体底面上的点 处沿着长方体表面爬到点 处.
答案
一 单选题
1. A
2. D
3. B
4. C
5. C
6. D
【解析】 是直角 斜边 上的高,
,
,
,
同理得:,
相等的角一共有 对.
故选D.
7. B
8. C
9. B
10. B
【解析】只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,
在直角三角形 中,根据勾股定理得:
;
,
蚂蚁爬行的最短距离是 .
11. B
【解析】
可整理为 ,
.
所以 .
二 填空题
12. 互余
13. ,, ; ,,
14.
【解析】筷子在杯里部分的最长长度为 ,所以筷子在杯子外面的最短长度为 .
15.
【解析】提示:
设 为 ,则 .
16.
【解析】由已知得 ,,;
在根据图形可得到 ,,,,,,
每三个一组,由于 ,则 ,然后把 加上( +1)即可.
三 解答题
17. 在 中,
,
.
18. ①:;
②:;
③:.
19. 在 中,,
,
在 中,,
,
20. (1)
【解析】,
,
,
,即 ,所以选择路线 较短.
(2) ① ;
② .
,即 .
所以选择路线 较短.
21. (1) 如图①,将正方体的“前面”和“右面”展开在同一平面上,连接 ,最短路程就是线段 的长.
由题意,得 .
.
在 中,由勾股定理,得 .
蚂蚁需要爬行的最短路程为 .
(2) 情况一:如图②,将长方体的“前面”和“右面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
情况二:如图③,将长方体的“前面”和“上面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
情况三:如图④,将长方体的“下面”和“右面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
,
蚂蚁需要爬行的最短路程为 .
第1页(共9 页)
一、单选题(共11小题)
1. 以下列各组线段为边作三角形,不能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
2. 已知一个直角三角形的两边长分别为 和 ,则第三边长的是
A. B. C. D. 或
3. 若 中,,且 ,,则 的值是
A. B. C. D.
4. 如图,已知正方形 的面积为 ,正方形 的面积为 ,则正方形 的面积为
A. B. C. D.
5. 给定下列条件,不能判定三角形是直角三角形的是
A. B.
C. D.
6. 如图, 是直角 斜边 上的高,,图中相等的角共有
A. 对 B. 对 C. 对 D. 对
7. 如图所示,在 中,,, 交 于点 .若 ,则
A. B. C. D.
8. 如图是一个四级台阶,它的每一级的长、宽、高分别为 ,,, 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
9. 2015年是国际“光”年,某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点 到顶点 镶有一圈金属丝,已知此三棱镜的高为 ,底面边长为 ,则这圈金属丝的长度至少为
A. B. C. D.
10. 如图,长方体的长为 宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是
A. B. C. D.
11. 已知 的三边 ,, 满足 ,则 为
A. 等腰三角形 B. 正三角形
C. 直角三角形 D. 等腰直角三角形
二、填空题(共5小题)
12. 直角三角形的两个锐角 .
13. 除 ,, 外,请你再写出两组勾股数: .
14. 如图,将一根 的筷子,置于底面直径为 ,高 的圆柱形水杯中,则筷子露在杯子外面的最短长度是 .
15. 如图所示,铁路沿线上有 , 两站(视为直线上的两点),, 两站相距 千米,, 为铁路同旁的两个蔬菜基地(视为两个点), 于点 , 于点 .已知 千米, 千米,现要在铁路 上建一个蔬菜加工厂 ,使蔬菜基地 , 到 的距离相等,则 站应建在距 站 千米的地方.
16. 如图,等腰 中,,,且 边在直线 上,将 绕点 顺时针旋转到位置 ① 可得到点 ,此时 ;将位置 ① 的三角形绕点 顺时针旋转到位置 ②,可得到点 ,此时 ;将位置 ② 的三角形绕点 顺时针旋转到位置 ③,可得到点 ,此时 ;,按此规律继续旋转,直至得到点 为止.则 .
三、解答题(共5小题)
17. 在 中,,若 ,,求 的长.
18. 分别写出 个图中的面积 ,, 之间的关系.
19. 一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
20. 如图①,圆柱的底面半径为 ,圆柱高 为 , 是底面直径,求一只蚂蚁从点 出发沿圆柱表面爬行到点 的最短路线,小明设计了两条路线:
路线 :高线 底面直径 ,如图①所示,设长度为 .
路线 :侧面展开图中的线段 ,如图②所示,设长度为 .
请按照小明的思路补充下面解题过程:
(1)解:,
;
.
(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为 ,高 为 ”继续按前面的路线进行计算.(结果保留 )
①此时,路线 ;
路线 .
②选择哪条路线较短 试说明理由.
21. 叶老师在与学生进行“蚂蚁怎样爬路程最短”的课题研究时,设计了以下两个问题.请你根据下面所给的重要条件分别求出蚂蚁需要爬行的最短路程(结果保留根号).
(1)如图①,正方体的棱长为 ,一只蚂蚁欲从正方体底面上的点 处沿着正方体表面爬到点 处;
(2)如图②,长方体的长和宽都为 ,高为 ,一只蚂蚁欲从长方体底面上的点 处沿着长方体表面爬到点 处.
答案
一 单选题
1. A
2. D
3. B
4. C
5. C
6. D
【解析】 是直角 斜边 上的高,
,
,
,
同理得:,
相等的角一共有 对.
故选D.
7. B
8. C
9. B
10. B
【解析】只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第 个图:
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,
在直角三角形 中,根据勾股定理得:
;
,
蚂蚁爬行的最短距离是 .
11. B
【解析】
可整理为 ,
.
所以 .
二 填空题
12. 互余
13. ,, ; ,,
14.
【解析】筷子在杯里部分的最长长度为 ,所以筷子在杯子外面的最短长度为 .
15.
【解析】提示:
设 为 ,则 .
16.
【解析】由已知得 ,,;
在根据图形可得到 ,,,,,,
每三个一组,由于 ,则 ,然后把 加上( +1)即可.
三 解答题
17. 在 中,
,
.
18. ①:;
②:;
③:.
19. 在 中,,
,
在 中,,
,
20. (1)
【解析】,
,
,
,即 ,所以选择路线 较短.
(2) ① ;
② .
,即 .
所以选择路线 较短.
21. (1) 如图①,将正方体的“前面”和“右面”展开在同一平面上,连接 ,最短路程就是线段 的长.
由题意,得 .
.
在 中,由勾股定理,得 .
蚂蚁需要爬行的最短路程为 .
(2) 情况一:如图②,将长方体的“前面”和“右面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
情况二:如图③,将长方体的“前面”和“上面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
情况三:如图④,将长方体的“下面”和“右面”展开在同一平面上,连接 .
由题意,得 ,.
.
在 中,由勾股定理,得 .
,
蚂蚁需要爬行的最短路程为 .
第1页(共9 页)
