鲁教版九年级数学上册第1章反比例函数同步辅导(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册第1章反比例函数同步辅导(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 163.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-13 07:47:29 | ||
图片预览


文档简介
鲁教版九年级数学上册第1章反比例函数同步辅导(含答案)
一、定义:我们把形如 叫做反比例函数
1.下列关于y与x的表达式中,反映y是x的反比例函数的是( )
A.y=4x B. =﹣2 C. xy=4 D. y=4x﹣3
2.下列函数中,不是反比例函数的是( )
A.y=﹣ B. y= C. y= D. 3xy=2
3.若函数为反比例函数,则m的值为( )
A.±1 B. 1 C. D. ﹣1
4.已知y=(a﹣1)是反比例函数,则a= .
5.若函数y=(m+2)x|m|﹣3是反比例函数,则m的值为 .
二、图像与性质: 。
6、函数 的图像在二、四象限,则m的取值范围是 ____ 。
7、反比例函数,它的图象在一、三象限,则m= ____。
8、在同一直角坐标系中,函数y=﹣与y=ax+1(a≠0)的图象可能是( )
A.B.C.D.
9、若点(-2,y1)(-1,y2)(2,y3)在反比例函数的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y1
10、在同一直角坐标系中,一次函数y=kx﹣k与反比例函数y=(k≠0)的图象大致是( )
A.B.C.D.
11、关于反比例函数y=﹣,下列说法正确的是( )
A.图象过(1,2)点 B. 图象在第一、三象限
C.当x>0时,y随x的增大而减小 D. 当x<0时,y随x的增大而增大
三、k的几何意义: 。
12、(2015 黔西南州)如图,点A是反比例函数y=图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k= .
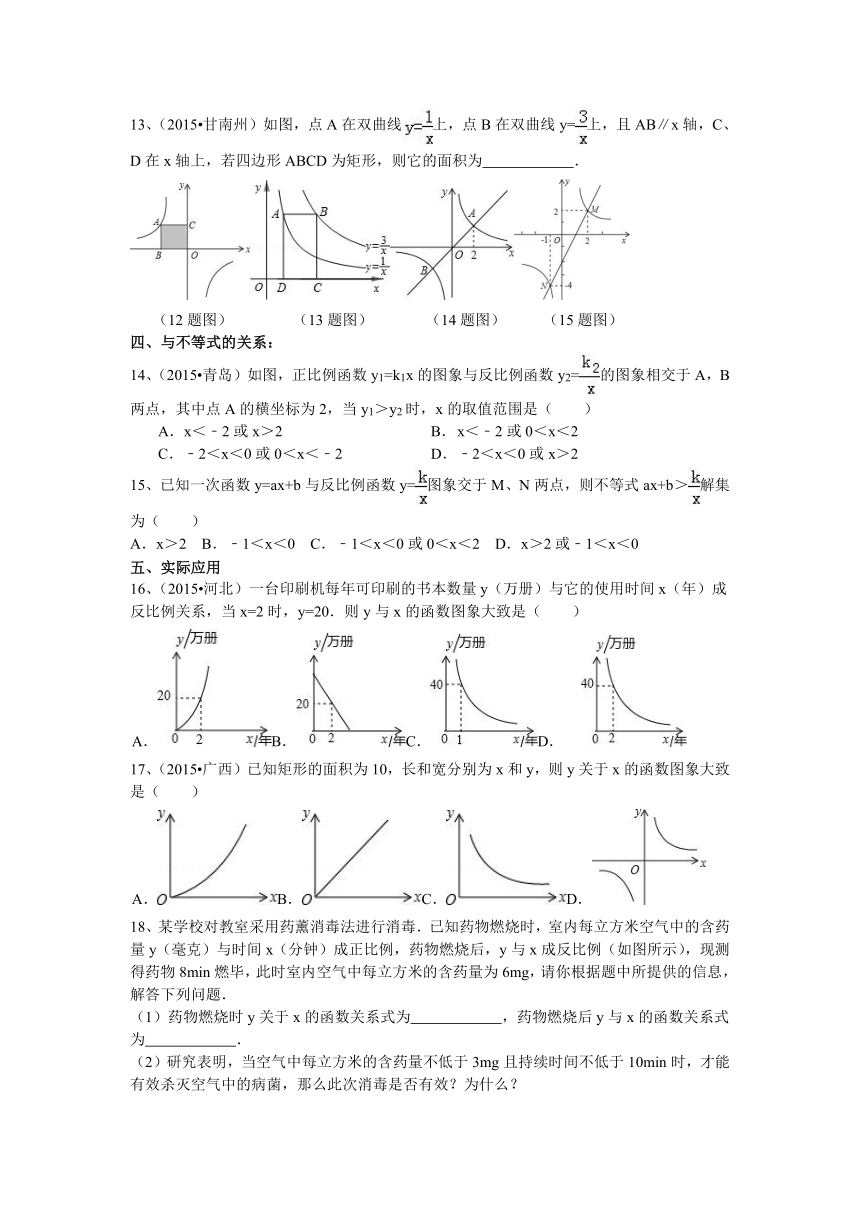
13、(2015 甘南州)如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
(12题图) (13题图) (14题图) (15题图)
四、与不等式的关系:
14、(2015 青岛)如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
A.x<﹣2或x>2 B. x<﹣2或0<x<2
C.﹣2<x<0或0<x<﹣2 D. ﹣2<x<0或x>2
15、已知一次函数y=ax+b与反比例函数y=图象交于M、N两点,则不等式ax+b>解集为( )
A.x>2 B.﹣1<x<0 C.﹣1<x<0或0<x<2 D.x>2或﹣1<x<0
五、实际应用
16、(2015 河北)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
17、(2015 广西)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C. D.
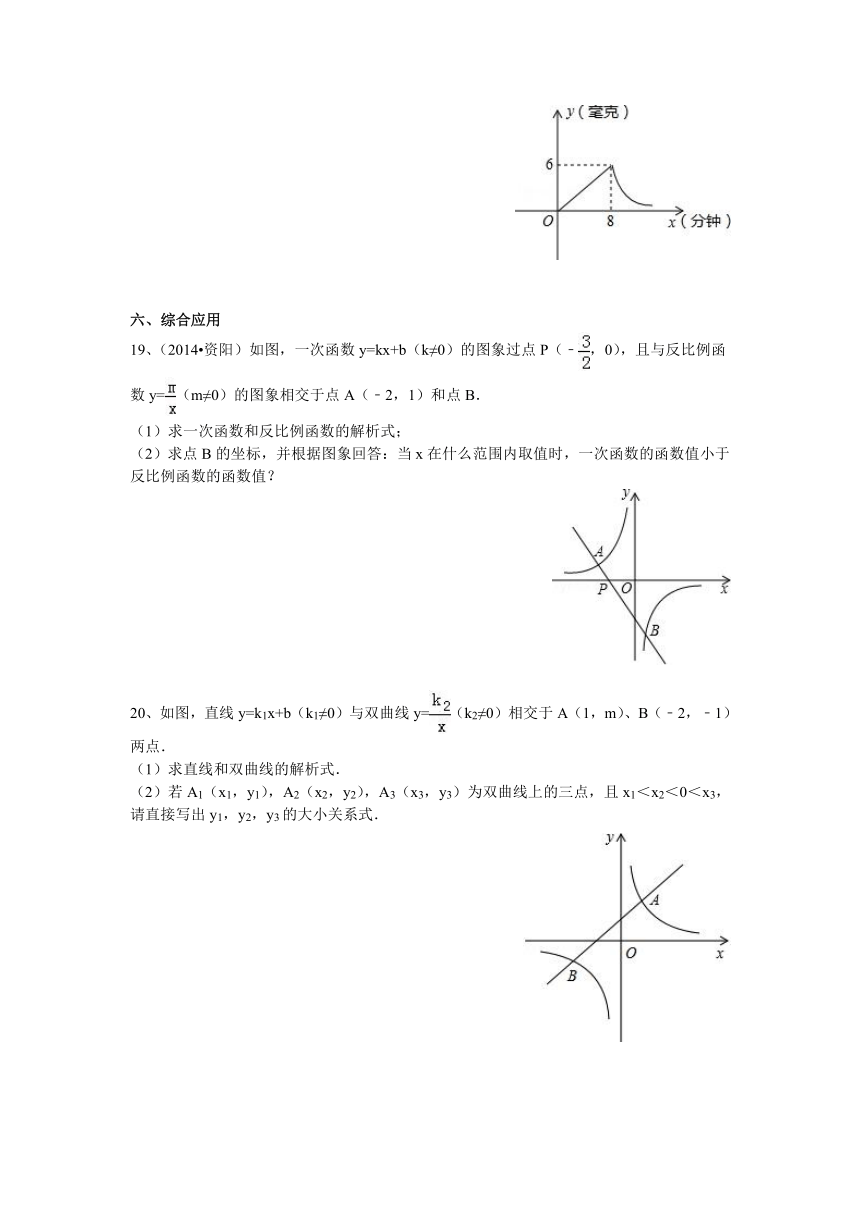
18、某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请你根据题中所提供的信息,解答下列问题.
(1)药物燃烧时y关于x的函数关系式为 ,药物燃烧后y与x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
六、综合应用
19、(2014 资阳)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
20、如图,直线y=k1x+b(k1≠0)与双曲线y=(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
七、全面练习
21、(2015 台州)若反比例函数y=的图象经过点(2,﹣1),则该反比例函数的图象在
A.第一、二象限 B. 第一、三象限 C. 第二、三象限 D. 第二、四象限
22、在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是()
A.﹣1 B. 1 C. 2 D. 3
23、(2015 娄底)反比例函数y=﹣的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( )
A.y1<y2<0 B. y1<0<y2 C. y1>y2>0 D. y1>0>y2
24、(2015 武汉)在反比例函数y=图象上有两点A(x1,y1),B (x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m> B. m< C. m≥ D. m≤
25、如图,函数与y2=k2x的图象相交于点A(1,2)和点B,当y1>y2时的自变量x的取值范围是( )
A.x>1 B.﹣1<x<0 C.﹣1<x<0或x>1 D.x<﹣1或0<x<1
26、(2015 衡阳)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
27、如图,直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值.
(2)求△OBC的面积.
28、(2015 黔东南州)如图,已知反比例函数y=与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.
29.如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数(k≠0)的图象经过点C.
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.
30.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
参考答案
1.C 2.C 3.D 4.-1 5.2 6、m<2 7、3 8、B 9、B
10、A 11、D 12、 4 13、2 14、D 15、D 16、C.17、C.
18、解:(1)∵药物燃烧时y与时间x成正比例,∴设 y=kx
∵(8,6)在y=kx上,8k=6,∴k=,∴y=x;
∵药物燃烧完毕后,y与x成反比例∴设y=,
∵(8,6)在 y=上,∴k=6×8=48;∴y=;故答案为:y=x,y=;
(2)3=x,x=4, 3=, x=16,16﹣4=12>10,所以此次消毒有效.
19、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
20、解:(1)∵双曲线y=经过点B(﹣2,﹣1),∴k2=2,∴双曲线的解析式为:y=,
∵点A(1,m)在双曲线y=上,∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得,
解得:,∴直线的解析式为:y=x+1;
(2)∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3.
21、D 22、A 23、D 24、A 25、D
26、解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,将(4,8)代入得:8=,
解得:a=32,故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
27、解:(1)∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(1,a),
∴先将A(1,a)代入直线y=2x,得:a=2
∴A(1,2),
将A(1,2)代入反比例函数y=中得:k=2,∴y=;
(2)∵B是反比例函数y=图象上的点,且BC⊥x轴于点C,
∴△BOC的面积=|k|=×2=1.
28、解:(1)∵已知反比例函数y=与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4),
∴﹣k+4=k,解得k=2,
故反比例函数的解析式为y=,
又知A(1,2)在一次函数y=x+b的图象上,故2=1+b,解得b=1,
故一次函数的解析式为y=x+1;
(2)由题意得:,解得x=﹣2或1,∴B(﹣2,﹣1),
令y=0,得x+1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△A0B=S△A0C+S△C0B=×1×2+×1×1=1+=.
29.解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,
∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3),
∴k=5×(﹣3)=﹣15,
∴反比例函数的解析式为;
(2)设点P到AD的距离为h.
∵△PAD的面积恰好等于正方形ABCD的面积,∴,解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,,
∴点P的坐标为(,12),
②当点P在第四象限时,yP=﹣(h﹣2)=﹣8,
此时,,
∴点P的坐标为(,﹣8).
综上所述,点P的坐标为(,12)或(,﹣8).
30.解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,即S△OCD=xy=k,
由(1)知k=6,∴S△OCD=k=3.
一、定义:我们把形如 叫做反比例函数
1.下列关于y与x的表达式中,反映y是x的反比例函数的是( )
A.y=4x B. =﹣2 C. xy=4 D. y=4x﹣3
2.下列函数中,不是反比例函数的是( )
A.y=﹣ B. y= C. y= D. 3xy=2
3.若函数为反比例函数,则m的值为( )
A.±1 B. 1 C. D. ﹣1
4.已知y=(a﹣1)是反比例函数,则a= .
5.若函数y=(m+2)x|m|﹣3是反比例函数,则m的值为 .
二、图像与性质: 。
6、函数 的图像在二、四象限,则m的取值范围是 ____ 。
7、反比例函数,它的图象在一、三象限,则m= ____。
8、在同一直角坐标系中,函数y=﹣与y=ax+1(a≠0)的图象可能是( )
A.B.C.D.
9、若点(-2,y1)(-1,y2)(2,y3)在反比例函数的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y1
10、在同一直角坐标系中,一次函数y=kx﹣k与反比例函数y=(k≠0)的图象大致是( )
A.B.C.D.
11、关于反比例函数y=﹣,下列说法正确的是( )
A.图象过(1,2)点 B. 图象在第一、三象限
C.当x>0时,y随x的增大而减小 D. 当x<0时,y随x的增大而增大
三、k的几何意义: 。
12、(2015 黔西南州)如图,点A是反比例函数y=图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k= .
13、(2015 甘南州)如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
(12题图) (13题图) (14题图) (15题图)
四、与不等式的关系:
14、(2015 青岛)如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
A.x<﹣2或x>2 B. x<﹣2或0<x<2
C.﹣2<x<0或0<x<﹣2 D. ﹣2<x<0或x>2
15、已知一次函数y=ax+b与反比例函数y=图象交于M、N两点,则不等式ax+b>解集为( )
A.x>2 B.﹣1<x<0 C.﹣1<x<0或0<x<2 D.x>2或﹣1<x<0
五、实际应用
16、(2015 河北)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A.B.C.D.
17、(2015 广西)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A.B.C. D.
18、某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请你根据题中所提供的信息,解答下列问题.
(1)药物燃烧时y关于x的函数关系式为 ,药物燃烧后y与x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
六、综合应用
19、(2014 资阳)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
20、如图,直线y=k1x+b(k1≠0)与双曲线y=(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(1)求直线和双曲线的解析式.
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.
七、全面练习
21、(2015 台州)若反比例函数y=的图象经过点(2,﹣1),则该反比例函数的图象在
A.第一、二象限 B. 第一、三象限 C. 第二、三象限 D. 第二、四象限
22、在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是()
A.﹣1 B. 1 C. 2 D. 3
23、(2015 娄底)反比例函数y=﹣的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( )
A.y1<y2<0 B. y1<0<y2 C. y1>y2>0 D. y1>0>y2
24、(2015 武汉)在反比例函数y=图象上有两点A(x1,y1),B (x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m> B. m< C. m≥ D. m≤
25、如图,函数与y2=k2x的图象相交于点A(1,2)和点B,当y1>y2时的自变量x的取值范围是( )
A.x>1 B.﹣1<x<0 C.﹣1<x<0或x>1 D.x<﹣1或0<x<1
26、(2015 衡阳)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
27、如图,直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值.
(2)求△OBC的面积.
28、(2015 黔东南州)如图,已知反比例函数y=与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.
29.如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数(k≠0)的图象经过点C.
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.
30.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
参考答案
1.C 2.C 3.D 4.-1 5.2 6、m<2 7、3 8、B 9、B
10、A 11、D 12、 4 13、2 14、D 15、D 16、C.17、C.
18、解:(1)∵药物燃烧时y与时间x成正比例,∴设 y=kx
∵(8,6)在y=kx上,8k=6,∴k=,∴y=x;
∵药物燃烧完毕后,y与x成反比例∴设y=,
∵(8,6)在 y=上,∴k=6×8=48;∴y=;故答案为:y=x,y=;
(2)3=x,x=4, 3=, x=16,16﹣4=12>10,所以此次消毒有效.
19、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
20、解:(1)∵双曲线y=经过点B(﹣2,﹣1),∴k2=2,∴双曲线的解析式为:y=,
∵点A(1,m)在双曲线y=上,∴m=2,即A(1,2),
由点A(1,2),B(﹣2,﹣1)在直线y=k1x+b上,得,
解得:,∴直线的解析式为:y=x+1;
(2)∵A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,
∴A1与A2在第三象限,A3在第一象限,即y1<0,y2<0,y3>0,
则y2<y1<y3.
21、D 22、A 23、D 24、A 25、D
26、解:(1)当0≤x≤4时,设直线解析式为:y=kx,将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设直反比例函数解析式为:y=,将(4,8)代入得:8=,
解得:a=32,故反比例函数解析式为:y=;
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
27、解:(1)∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点A(1,a),
∴先将A(1,a)代入直线y=2x,得:a=2
∴A(1,2),
将A(1,2)代入反比例函数y=中得:k=2,∴y=;
(2)∵B是反比例函数y=图象上的点,且BC⊥x轴于点C,
∴△BOC的面积=|k|=×2=1.
28、解:(1)∵已知反比例函数y=与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4),
∴﹣k+4=k,解得k=2,
故反比例函数的解析式为y=,
又知A(1,2)在一次函数y=x+b的图象上,故2=1+b,解得b=1,
故一次函数的解析式为y=x+1;
(2)由题意得:,解得x=﹣2或1,∴B(﹣2,﹣1),
令y=0,得x+1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△A0B=S△A0C+S△C0B=×1×2+×1×1=1+=.
29.解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,
∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3),
∴k=5×(﹣3)=﹣15,
∴反比例函数的解析式为;
(2)设点P到AD的距离为h.
∵△PAD的面积恰好等于正方形ABCD的面积,∴,解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,,
∴点P的坐标为(,12),
②当点P在第四象限时,yP=﹣(h﹣2)=﹣8,
此时,,
∴点P的坐标为(,﹣8).
综上所述,点P的坐标为(,12)或(,﹣8).
30.解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,即S△OCD=xy=k,
由(1)知k=6,∴S△OCD=k=3.
