17.1 勾股定理 课后练习题(含答案)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 课后练习题(含答案)2023-2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 285.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览

文档简介
第十七章 勾股定理
17.1 勾股定理
一、选择题
1.在△ABC中,∠A=90°,则下列各式中不成立的是 ( )
A.BC2=AB2+AC2 B.AB2=AC2+BC2
C.AB2=BC2-AC2 D.AC2=BC2-AB2
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是 ( )
A.13 m B.17 m C.18 m D.25 m
4.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,4,6,8,10,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.2,8,10 B.4,6,10 C.6,8,10 D.4,4,8
5.如图,在△ABC中,∠C=90°,AC=3,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( )
A.3 B.+1 C.-1 D.+1
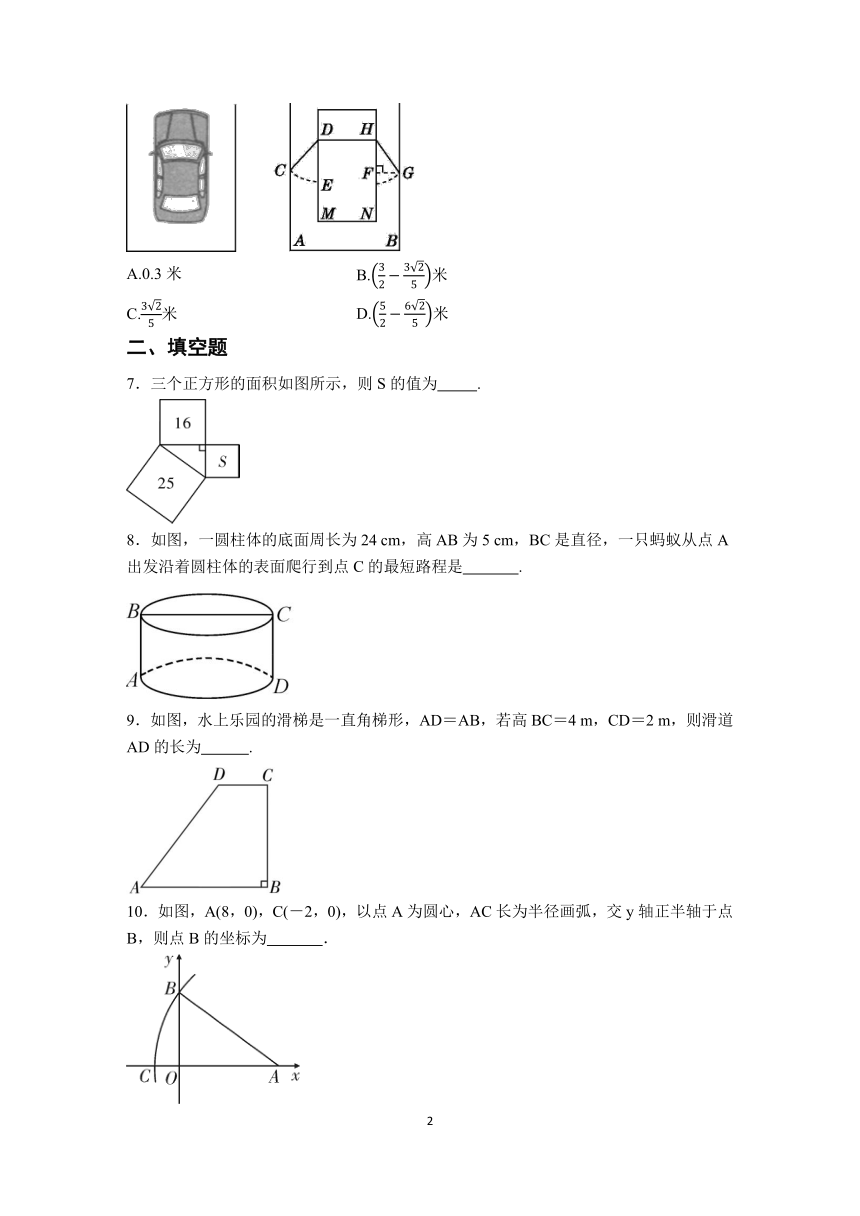
6.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
二、填空题
7.三个正方形的面积如图所示,则S的值为 .
8.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 .
9.如图,水上乐园的滑梯是一直角梯形,AD=AB,若高BC=4 m,CD=2 m,则滑道AD的长为 .
10.如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
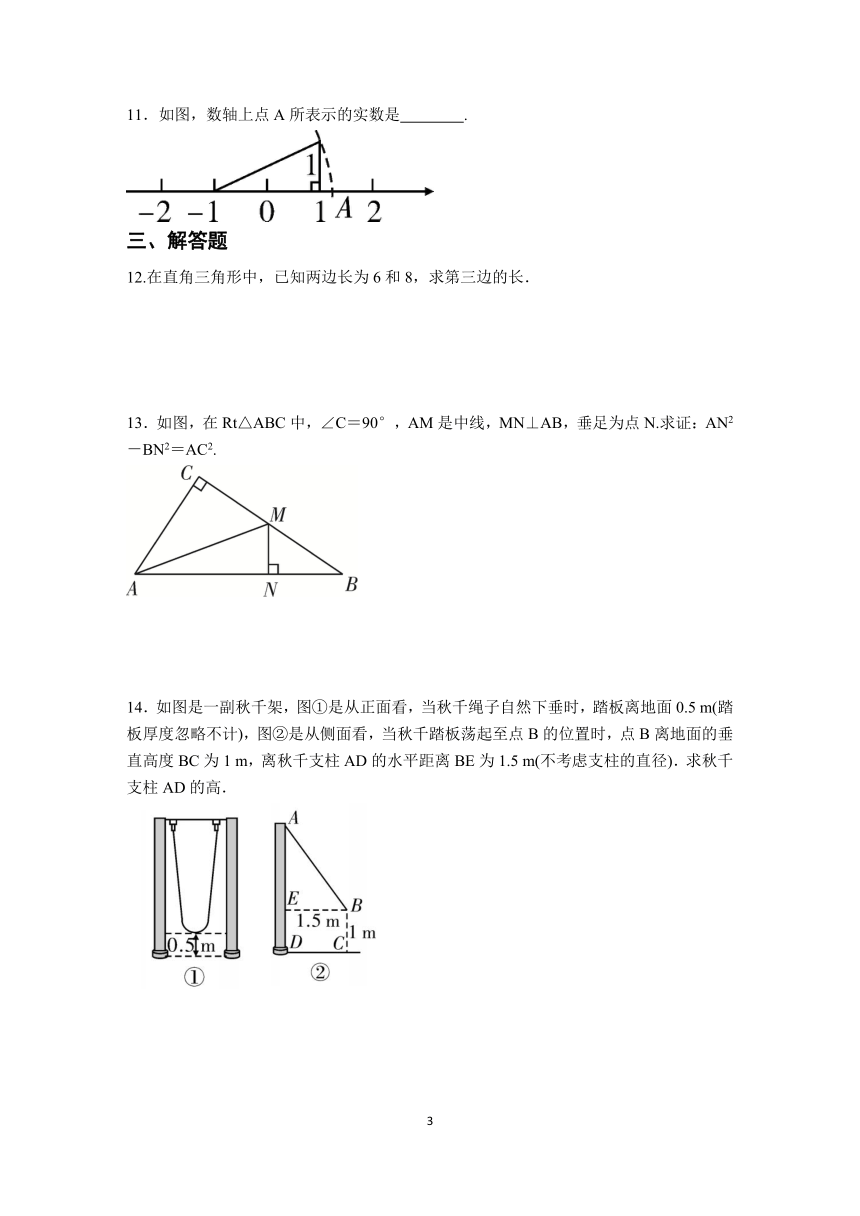
11.如图,数轴上点A所表示的实数是 .
三、解答题
12.在直角三角形中,已知两边长为6和8,求第三边的长.
13.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N.求证:AN2-BN2=AC2.
14.如图是一副秋千架,图①是从正面看,当秋千绳子自然下垂时,踏板离地面0.5 m(踏板厚度忽略不计),图②是从侧面看,当秋千踏板荡起至点B的位置时,点B离地面的垂直高度BC为1 m,离秋千支柱AD的水平距离BE为1.5 m(不考虑支柱的直径).求秋千支柱AD的高.
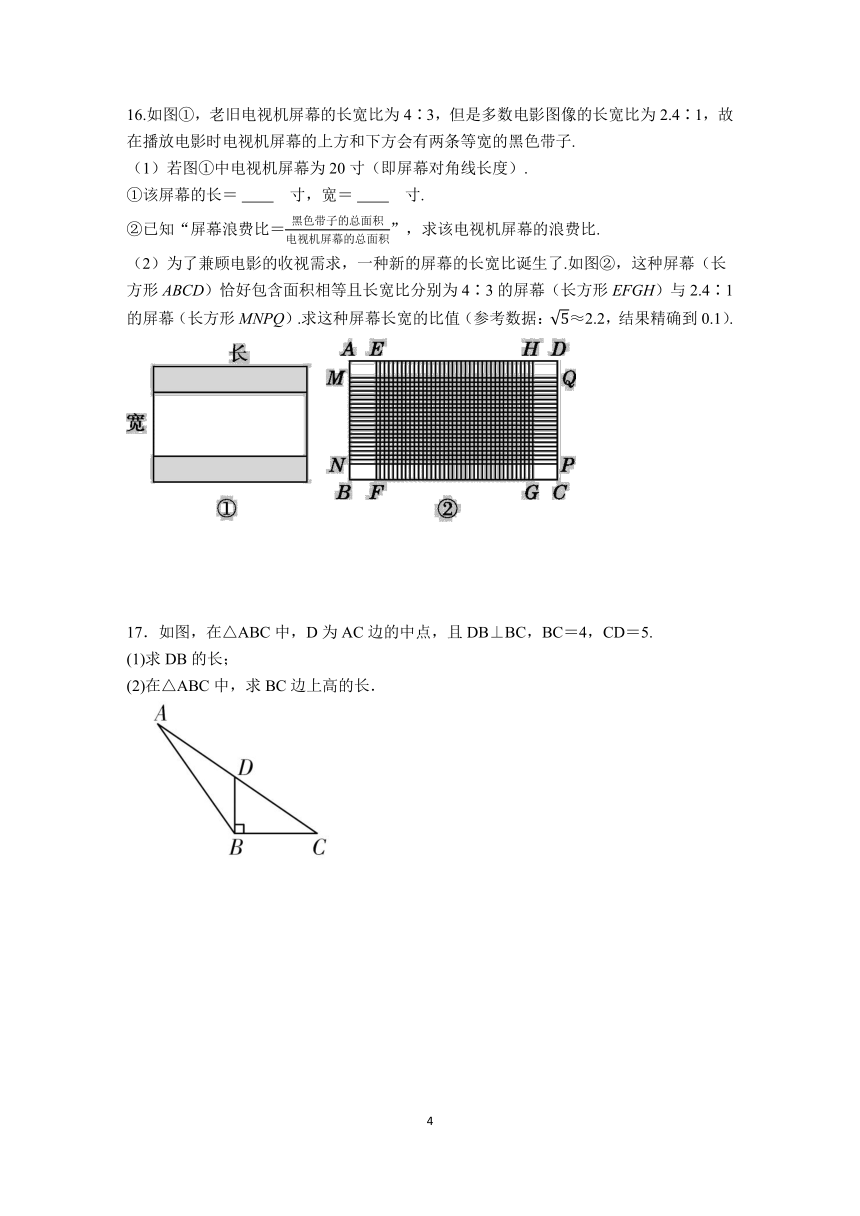
16.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
17.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
9
参考答案
一、选择题
1.在△ABC中,∠A=90°,则下列各式中不成立的是 ( B )
A.BC2=AB2+AC2 B.AB2=AC2+BC2
C.AB2=BC2-AC2 D.AC2=BC2-AB2
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( A )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是 ( B )
A.13 m B.17 m C.18 m D.25 m
4.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,4,6,8,10,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( B )
A.2,8,10 B.4,6,10 C.6,8,10 D.4,4,8
5.如图,在△ABC中,∠C=90°,AC=3,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( D )
A.3 B.+1 C.-1 D.+1
6.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
二、填空题
7.三个正方形的面积如图所示,则S的值为 .
【答案】9
8.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 .
【答案】13cm
9.如图,水上乐园的滑梯是一直角梯形,AD=AB,若高BC=4 m,CD=2 m,则滑道AD的长为 .
【答案】5m
10.如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
【答案】(0,6)
11.如图,数轴上点A所表示的实数是 .
【答案】-1
三、解答题
12.在直角三角形中,已知两边长为6和8,求第三边的长.
设第三边为x,当x为斜边时,由勾股定理得x2=62+82.
∴x====10.
当x为直角边时,由勾股定理得x2+62=82.
∴x====2.
∴这个三角形的第三边长为10或2.
13.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N.求证:AN2-BN2=AC2.
证明:∵MN⊥AB于点N,
∴AN2=AM2-MN2,BN2=BM2-MN2.
∴AN2-BN2=AM2-BM2.
又∵∠C=90°,∴AM2=AC2+CM2.
∴AN2-BN2=AC2+CM2-BM2.
又∵AM是△ABC的中线,
∴CM=BM.∴AN2-BN2=AC2.
14.如图是一副秋千架,图①是从正面看,当秋千绳子自然下垂时,踏板离地面0.5 m(踏板厚度忽略不计),图②是从侧面看,当秋千踏板荡起至点B的位置时,点B离地面的垂直高度BC为1 m,离秋千支柱AD的水平距离BE为1.5 m(不考虑支柱的直径).求秋千支柱AD的高.
解:设AD=x m.由题意,得
AB=(x-0.5) m,AE=(x-1) m.
在Rt△ABE中,AE2+BE2=AB2,
即(x-1)2+1.52=(x-0.5)2.
解得x=3.
答:秋千支柱AD的高为3 m.
15.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
解:(1)①16;12
②设在该屏幕上播放长宽比为2.4∶1的视频时,视频的宽为a寸.
∴16∶a=2.4∶1,解得a=.
∴黑色带子的宽的和=12-=(寸).
∴屏幕浪费比==.
(2)由题意得=,=,∴PQ=BC,FG=EF.
∵S长方形EFGH=S长方形MNPQ,
∴BC·BC=EF·EF.
∴=,
∴=≈1.8.
答:这种屏幕长宽的比值约为1.8.
16.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
解:(1)∵DB⊥BC,∴∠DBC=90°.
又∵BC=4,CD=5,
∴在Rt△DBC中,
由勾股定理得BD=
==3.
(2)在△ABC中,求BC边上高的长.
(2)延长BD至点E,使ED=BD,连接AE.
∵D是AC的中点,∴AD=CD.
易证△BDC≌△EDA(SAS),
∴∠AED=∠DBC=90°,∴BE⊥AE,
∴BE等于△ABC中BC边上的高,
∴BE=DE+BD=2BD=6.
即在△ABC中,BC边上高的长为6.
17.1 勾股定理
一、选择题
1.在△ABC中,∠A=90°,则下列各式中不成立的是 ( )
A.BC2=AB2+AC2 B.AB2=AC2+BC2
C.AB2=BC2-AC2 D.AC2=BC2-AB2
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是 ( )
A.13 m B.17 m C.18 m D.25 m
4.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,4,6,8,10,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.2,8,10 B.4,6,10 C.6,8,10 D.4,4,8
5.如图,在△ABC中,∠C=90°,AC=3,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( )
A.3 B.+1 C.-1 D.+1
6.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
二、填空题
7.三个正方形的面积如图所示,则S的值为 .
8.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 .
9.如图,水上乐园的滑梯是一直角梯形,AD=AB,若高BC=4 m,CD=2 m,则滑道AD的长为 .
10.如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
11.如图,数轴上点A所表示的实数是 .
三、解答题
12.在直角三角形中,已知两边长为6和8,求第三边的长.
13.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N.求证:AN2-BN2=AC2.
14.如图是一副秋千架,图①是从正面看,当秋千绳子自然下垂时,踏板离地面0.5 m(踏板厚度忽略不计),图②是从侧面看,当秋千踏板荡起至点B的位置时,点B离地面的垂直高度BC为1 m,离秋千支柱AD的水平距离BE为1.5 m(不考虑支柱的直径).求秋千支柱AD的高.
16.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
17.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
9
参考答案
一、选择题
1.在△ABC中,∠A=90°,则下列各式中不成立的是 ( B )
A.BC2=AB2+AC2 B.AB2=AC2+BC2
C.AB2=BC2-AC2 D.AC2=BC2-AB2
2.为准备召开新年晚会,大宏搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离为( A )
A.0.7 m B.0.8 m C.0.9 m D.1.0 m
3.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,则地毯长度至少应是 ( B )
A.13 m B.17 m C.18 m D.25 m
4.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是2,4,6,8,10,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( B )
A.2,8,10 B.4,6,10 C.6,8,10 D.4,4,8
5.如图,在△ABC中,∠C=90°,AC=3,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( D )
A.3 B.+1 C.-1 D.+1
6.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
二、填空题
7.三个正方形的面积如图所示,则S的值为 .
【答案】9
8.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 .
【答案】13cm
9.如图,水上乐园的滑梯是一直角梯形,AD=AB,若高BC=4 m,CD=2 m,则滑道AD的长为 .
【答案】5m
10.如图,A(8,0),C(-2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为 .
【答案】(0,6)
11.如图,数轴上点A所表示的实数是 .
【答案】-1
三、解答题
12.在直角三角形中,已知两边长为6和8,求第三边的长.
设第三边为x,当x为斜边时,由勾股定理得x2=62+82.
∴x====10.
当x为直角边时,由勾股定理得x2+62=82.
∴x====2.
∴这个三角形的第三边长为10或2.
13.如图,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为点N.求证:AN2-BN2=AC2.
证明:∵MN⊥AB于点N,
∴AN2=AM2-MN2,BN2=BM2-MN2.
∴AN2-BN2=AM2-BM2.
又∵∠C=90°,∴AM2=AC2+CM2.
∴AN2-BN2=AC2+CM2-BM2.
又∵AM是△ABC的中线,
∴CM=BM.∴AN2-BN2=AC2.
14.如图是一副秋千架,图①是从正面看,当秋千绳子自然下垂时,踏板离地面0.5 m(踏板厚度忽略不计),图②是从侧面看,当秋千踏板荡起至点B的位置时,点B离地面的垂直高度BC为1 m,离秋千支柱AD的水平距离BE为1.5 m(不考虑支柱的直径).求秋千支柱AD的高.
解:设AD=x m.由题意,得
AB=(x-0.5) m,AE=(x-1) m.
在Rt△ABE中,AE2+BE2=AB2,
即(x-1)2+1.52=(x-0.5)2.
解得x=3.
答:秋千支柱AD的高为3 m.
15.如图①,老旧电视机屏幕的长宽比为4∶3,但是多数电影图像的长宽比为2.4∶1,故在播放电影时电视机屏幕的上方和下方会有两条等宽的黑色带子.
(1)若图①中电视机屏幕为20寸(即屏幕对角线长度).
①该屏幕的长= 寸,宽= 寸.
②已知“屏幕浪费比=”,求该电视机屏幕的浪费比.
(2)为了兼顾电影的收视需求,一种新的屏幕的长宽比诞生了.如图②,这种屏幕(长方形ABCD)恰好包含面积相等且长宽比分别为4∶3的屏幕(长方形EFGH)与2.4∶1的屏幕(长方形MNPQ).求这种屏幕长宽的比值(参考数据:≈2.2,结果精确到0.1).
解:(1)①16;12
②设在该屏幕上播放长宽比为2.4∶1的视频时,视频的宽为a寸.
∴16∶a=2.4∶1,解得a=.
∴黑色带子的宽的和=12-=(寸).
∴屏幕浪费比==.
(2)由题意得=,=,∴PQ=BC,FG=EF.
∵S长方形EFGH=S长方形MNPQ,
∴BC·BC=EF·EF.
∴=,
∴=≈1.8.
答:这种屏幕长宽的比值约为1.8.
16.如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
解:(1)∵DB⊥BC,∴∠DBC=90°.
又∵BC=4,CD=5,
∴在Rt△DBC中,
由勾股定理得BD=
==3.
(2)在△ABC中,求BC边上高的长.
(2)延长BD至点E,使ED=BD,连接AE.
∵D是AC的中点,∴AD=CD.
易证△BDC≌△EDA(SAS),
∴∠AED=∠DBC=90°,∴BE⊥AE,
∴BE等于△ABC中BC边上的高,
∴BE=DE+BD=2BD=6.
即在△ABC中,BC边上高的长为6.
