人教版八年级下册17.2 勾股定理的逆定理 课后练习题(含答案)
文档属性
| 名称 | 人教版八年级下册17.2 勾股定理的逆定理 课后练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览

文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( )
A.4,6,8 B.6,8,9
C.5,12,13 D.5,11,12
2.在下列各组数中,是勾股数的是 ( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是 ( )
A.正东或正西 B.正南
C.正北 D.正南或正北
4.下列各定理中有逆定理的是 ( )
A.两直线平行,同旁内角互补
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
5.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( )
A.10 B.11 C.12 D.13
二、填空题
7.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
8.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
9.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
10.一组勾股数,若其中两个为15,8,则第三个数为 .
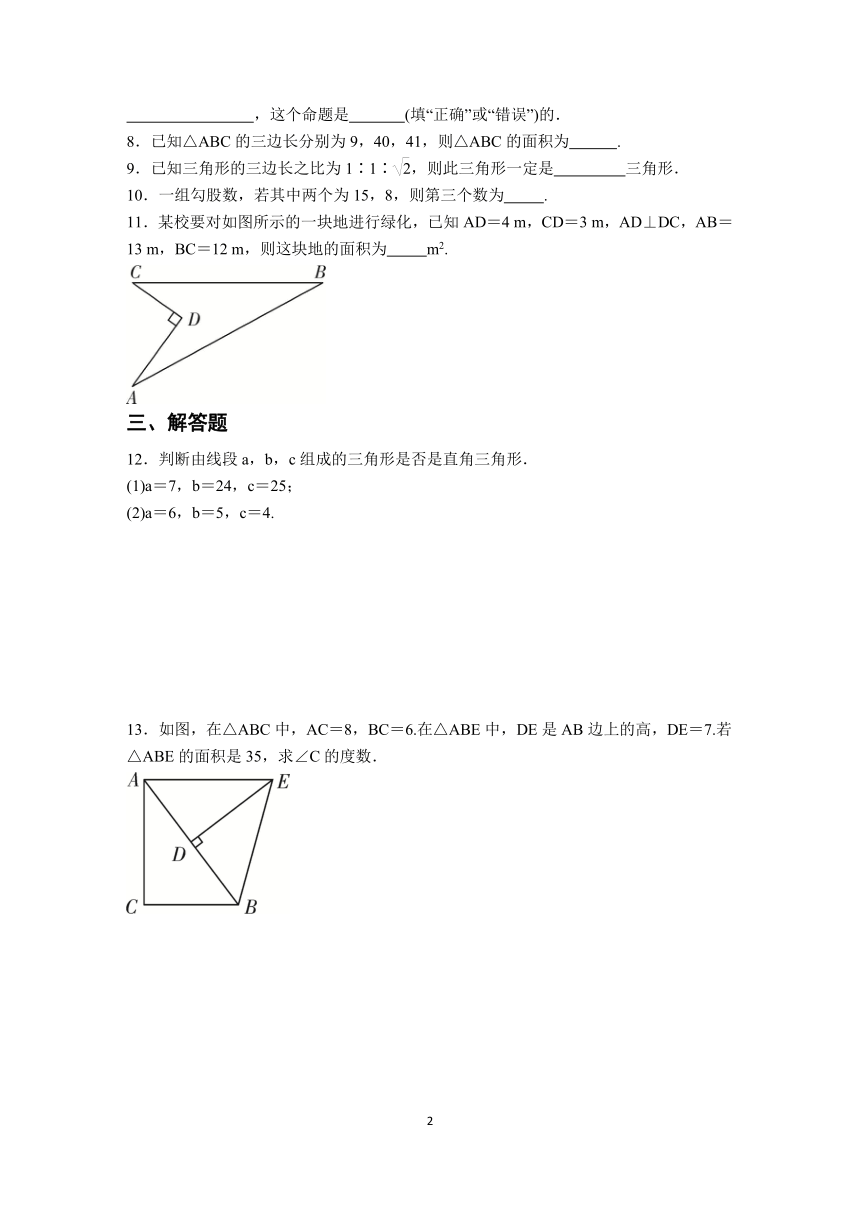
11.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
三、解答题
12.判断由线段a,b,c组成的三角形是否是直角三角形.
(1)a=7,b=24,c=25;
(2)a=6,b=5,c=4.
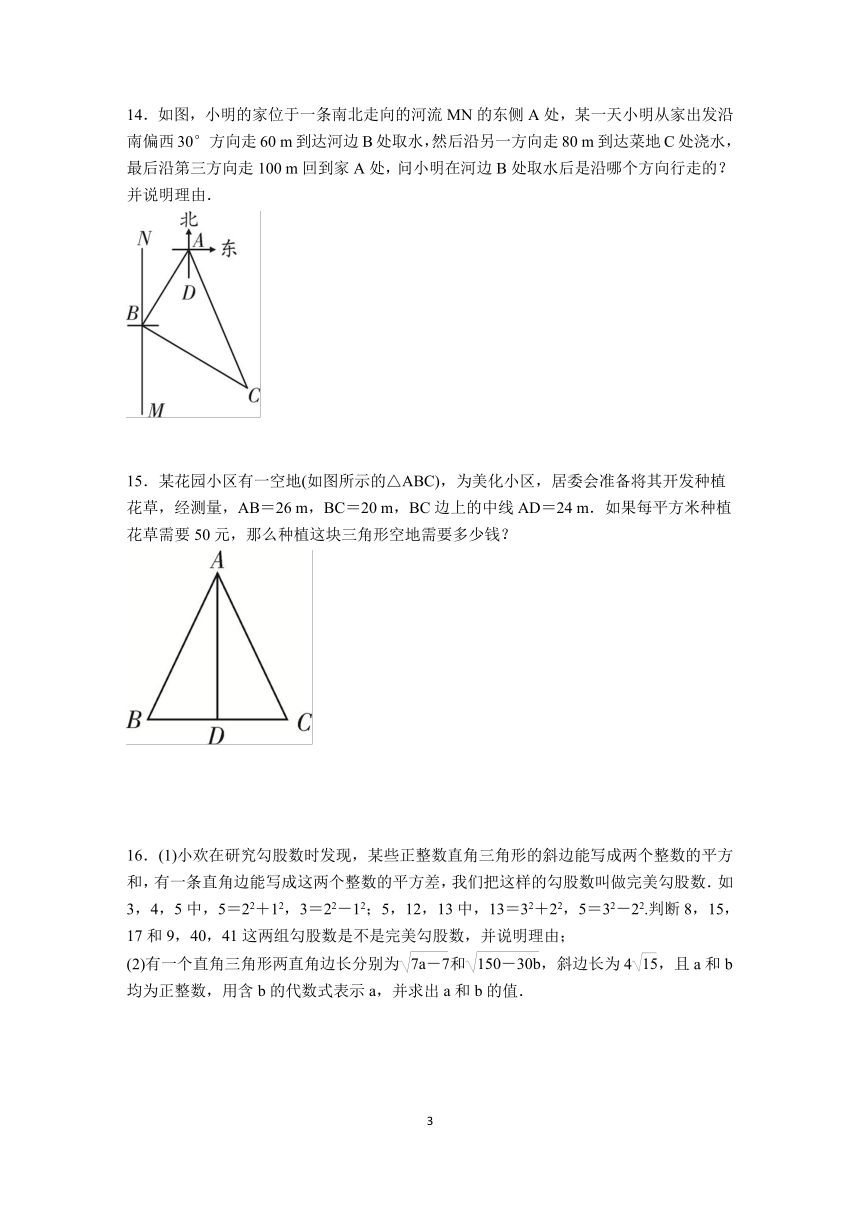
13.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
14.如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处,问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
15.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,那么种植这块三角形空地需要多少钱?
16.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
1
参考答案
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( C )
A.4,6,8 B.6,8,9
C.5,12,13 D.5,11,12
2.在下列各组数中,是勾股数的是 ( C )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是 ( D )
A.正东或正西 B.正南
C.正北 D.正南或正北
4.下列各定理中有逆定理的是 ( A )
A.两直线平行,同旁内角互补
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
5.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形 ( D )
A.1个 B.2个 C.3个 D.4个
6.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( D )
A.10 B.11 C.12 D.13
二、填空题
7.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
【答案】两边上的高相等的三角形是等腰三角形 正确
8.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
【答案】180
9.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
【答案】等腰直角
10.一组勾股数,若其中两个为15,8,则第三个数为 .
【答案】17
11.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
【答案】24
三、解答题
12.判断由线段a,b,c组成的三角形是否是直角三角形.
(1)a=7,b=24,c=25;
(2)a=6,b=5,c=4.
解:(1)∵a=7,b=24,c=25且a∴由线段a,b,c组成的三角形是直角三角形.
解:(2)∵a=6,b=5,c=4,且c∴由线段a,b,c组成的三角形不是直角三角形.
13.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
解:在△ABE中,
DE为AB边上的高,DE=7,
∴S△ABE=·AB·DE=35.
∴AB=10.∵AC=8,BC=6,
∴AC2+BC2=64+36=100=AB2.
∴△ABC为直角三角形.∴∠C=90°.
14.如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处,问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
解:小明在河边B处取水后是沿南偏东60°方向行走的,
理由:∵AB=60,
BC=80,AC=100,
∴AB2+BC2=AC2,∴∠ABC=90°,
∵∠NBA=∠BAD=30°,
∴∠MBC=60°.
15.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,那么种植这块三角形空地需要多少钱?
解:∵AD是中线,BC=20 m,∴BD=BC=10 m.
又∵102+242=262,即BD2+AD2=AB2,
∴△ABD是直角三角形.∴AD⊥BC.
∴S△ABC=BC·AD=×20×24=240(m2).
∵每平方米种植花草需要50元,
∴共需50×240=12 000(元).
答:种植这块三角形空地需要12 000元.
16.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
解:(1)∵17=42+12,15=42-12,
∴8,15,17是完美勾股数;
∵41=52+42,9=52-42,
∴9,40,41是完美勾股数.
(2)由勾股定理得7a-7+(150-30b)=16×15,∴a=.
由题意可知7a-7>0,150-30b>0,
∴a>1,0<b<5.∵a和b均为正整数,∴b的可能值为1,2,3,4.
当b=1时,a=,不是正整数,不合题意;
当b=2时,a=,不是正整数,不合题意;
当b=3时,a=,不是正整数,不合题意;
当b=4时,a=31,是正整数,
此时=,=.
∵()2+()2=240,(4)2=240,
∴()2+()2=(4)2,
∴b=4符合题意.即a=31,b=4.
17.2 勾股定理的逆定理
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( )
A.4,6,8 B.6,8,9
C.5,12,13 D.5,11,12
2.在下列各组数中,是勾股数的是 ( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是 ( )
A.正东或正西 B.正南
C.正北 D.正南或正北
4.下列各定理中有逆定理的是 ( )
A.两直线平行,同旁内角互补
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
5.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( )
A.10 B.11 C.12 D.13
二、填空题
7.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
8.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
9.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
10.一组勾股数,若其中两个为15,8,则第三个数为 .
11.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
三、解答题
12.判断由线段a,b,c组成的三角形是否是直角三角形.
(1)a=7,b=24,c=25;
(2)a=6,b=5,c=4.
13.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
14.如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处,问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
15.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,那么种植这块三角形空地需要多少钱?
16.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
1
参考答案
一、选择题
1.下列长度的三条线段能组成直角三角形的是 ( C )
A.4,6,8 B.6,8,9
C.5,12,13 D.5,11,12
2.在下列各组数中,是勾股数的是 ( C )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是 ( D )
A.正东或正西 B.正南
C.正北 D.正南或正北
4.下列各定理中有逆定理的是 ( A )
A.两直线平行,同旁内角互补
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
5.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形 ( D )
A.1个 B.2个 C.3个 D.4个
6.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( D )
A.10 B.11 C.12 D.13
二、填空题
7.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
【答案】两边上的高相等的三角形是等腰三角形 正确
8.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
【答案】180
9.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
【答案】等腰直角
10.一组勾股数,若其中两个为15,8,则第三个数为 .
【答案】17
11.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
【答案】24
三、解答题
12.判断由线段a,b,c组成的三角形是否是直角三角形.
(1)a=7,b=24,c=25;
(2)a=6,b=5,c=4.
解:(1)∵a=7,b=24,c=25且a
解:(2)∵a=6,b=5,c=4,且c
13.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
解:在△ABE中,
DE为AB边上的高,DE=7,
∴S△ABE=·AB·DE=35.
∴AB=10.∵AC=8,BC=6,
∴AC2+BC2=64+36=100=AB2.
∴△ABC为直角三角形.∴∠C=90°.
14.如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处,问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
解:小明在河边B处取水后是沿南偏东60°方向行走的,
理由:∵AB=60,
BC=80,AC=100,
∴AB2+BC2=AC2,∴∠ABC=90°,
∵∠NBA=∠BAD=30°,
∴∠MBC=60°.
15.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,那么种植这块三角形空地需要多少钱?
解:∵AD是中线,BC=20 m,∴BD=BC=10 m.
又∵102+242=262,即BD2+AD2=AB2,
∴△ABD是直角三角形.∴AD⊥BC.
∴S△ABC=BC·AD=×20×24=240(m2).
∵每平方米种植花草需要50元,
∴共需50×240=12 000(元).
答:种植这块三角形空地需要12 000元.
16.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
解:(1)∵17=42+12,15=42-12,
∴8,15,17是完美勾股数;
∵41=52+42,9=52-42,
∴9,40,41是完美勾股数.
(2)由勾股定理得7a-7+(150-30b)=16×15,∴a=.
由题意可知7a-7>0,150-30b>0,
∴a>1,0<b<5.∵a和b均为正整数,∴b的可能值为1,2,3,4.
当b=1时,a=,不是正整数,不合题意;
当b=2时,a=,不是正整数,不合题意;
当b=3时,a=,不是正整数,不合题意;
当b=4时,a=31,是正整数,
此时=,=.
∵()2+()2=240,(4)2=240,
∴()2+()2=(4)2,
∴b=4符合题意.即a=31,b=4.
