第十七章 勾股定理 章末复习题(含答案) 2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 第十七章 勾股定理 章末复习题(含答案) 2023-2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 00:00:00 | ||
图片预览



文档简介
第十七章 勾股定理
章末复习题
一、选择题
1.在直角三角形中,若勾为3,股为4,则弦为 ( )
A.5 B.6 C.7 D.8
2.在△ABC中,AB=,BC=,AC=,则 ( )
A.∠B+∠C=90° B.∠A+∠C=90°
C.∠A+∠B=90° D.∠B=∠C
3.下列命题的逆命题是真命题的是 ( )
A.如果两个角是直角,那么它们相等 B.全等三角形的面积相等
C.如果a>0,b>0,那么ab>0 D.两直线平行,内错角相等
4.下列定理中,没有逆定理的是 ( )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形两个锐角的和等于90°
5.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为 ( )
A. B. C.1 D.2
6.将长为8 cm的橡皮筋放置在水平桌面上,固定两端,然后把中点竖直向上拉升3 cm,则橡皮筋被拉长了 ( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10 m,BC=15 m,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要 ( )
A.75a元 B.50a元 C.a元 D.150a元
8.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
9.将一根25 cm长的细木棒放入长、宽、高分别为8 cm,6 cm,10 cm的长方体无盖盒子中,则细木棒在盒子外面的最短长度是 cm.
10.一个三角形的三边的比为5∶12∶13,它的周长为60 cm,则它的面积是 cm2.
11.有一长、宽、高分别为5 cm、4 cm、3 cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是 .
12.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕的△ABD折叠得到△AB'D,AB'与边BC交于点E,若△DEB'为直角三角形,则BD的长是 .
三、解答题
13.如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
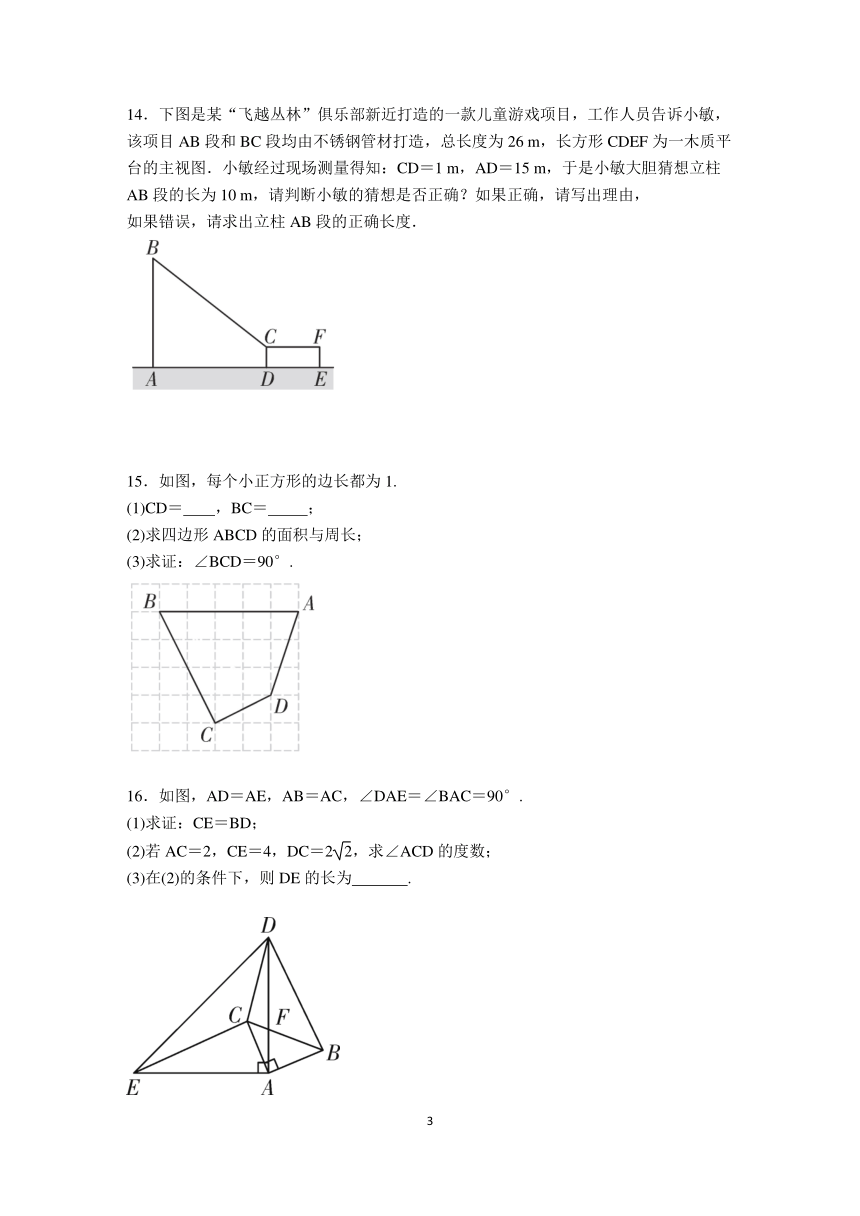
14.下图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26 m,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1 m,AD=15 m,于是小敏大胆猜想立柱AB段的长为10 m,请判断小敏的猜想是否正确?如果正确,请写出理由,
如果错误,请求出立柱AB段的正确长度.
15.如图,每个小正方形的边长都为1.
(1)CD= ,BC= ;
(2)求四边形ABCD的面积与周长;
(3)求证:∠BCD=90°.
16.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,则DE的长为 .
17.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
5
参考答案
一、选择题
1.在直角三角形中,若勾为3,股为4,则弦为 ( A )
A.5 B.6 C.7 D.8
2.在△ABC中,AB=,BC=,AC=,则 ( A )
A.∠B+∠C=90° B.∠A+∠C=90°
C.∠A+∠B=90° D.∠B=∠C
3.下列命题的逆命题是真命题的是 ( D )
A.如果两个角是直角,那么它们相等 B.全等三角形的面积相等
C.如果a>0,b>0,那么ab>0 D.两直线平行,内错角相等
4.下列定理中,没有逆定理的是 ( B )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形两个锐角的和等于90°
5.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为 ( B )
A. B. C.1 D.2
6.将长为8 cm的橡皮筋放置在水平桌面上,固定两端,然后把中点竖直向上拉升3 cm,则橡皮筋被拉长了 ( A )
A.2 cm B.3 cm C.4 cm D.5 cm
7.为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10 m,BC=15 m,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要 ( A )
A.75a元 B.50a元 C.a元 D.150a元
8.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( C )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
9.将一根25 cm长的细木棒放入长、宽、高分别为8 cm,6 cm,10 cm的长方体无盖盒子中,则细木棒在盒子外面的最短长度是 cm.
【答案】5
10.一个三角形的三边的比为5∶12∶13,它的周长为60 cm,则它的面积是 cm2.
【答案】120
11.有一长、宽、高分别为5 cm、4 cm、3 cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是 .
【答案】5 cm
12.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕的△ABD折叠得到△AB'D,AB'与边BC交于点E,若△DEB'为直角三角形,则BD的长是 .
【答案】2或5
三、解答题
13.如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
解:过点E作EF⊥BD,垂足为点F.
∵△DCE为等边三角形,
∴EF是△DCE的中线,
∴CF=CD=1.∴BF=BC+CF=2+1=3.
在Rt△EFC中,由勾股定理,得
EF2=EC2-CF2=22-12=3.
在Rt△EFB中,由勾股定理,得
BE2=BF2+EF2=32+3=12,∴BE=2.
14.下图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26 m,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1 m,AD=15 m,于是小敏大胆猜想立柱AB段的长为10 m,请判断小敏的猜想是否正确?如果正确,请写出理由,
如果错误,请求出立柱AB段的正确长度.
解:错误.延长FC交AB于点G,则CG⊥AB,
AG=CD=1 m,
GC=AD=15 m,
设BG=x m,则BC=(26-1-x)m,
在Rt△BGC中,∵BG2+CG2=CB2,
∴x2+152=(26-1-x)2,解得x=8,
∴BA=BG+GA=8+1=9(m),
∴小敏的猜想错误,立柱AB段的正确长度为9 m.
15.如图,每个小正方形的边长都为1.
(1)CD= ,BC= ;
【答案】 2
(2)求四边形ABCD的面积与周长;
(3)求证:∠BCD=90°.
(2)解:∵AB=5,AD==,
∴四边形ABCD的周长为
2++5+=+3+5,
∴S四边形ABCD=4×5-×2×4-×1×2- ×1×3-1×1=12.5.
(3)证明:连接BD,则BD2=32+42=25.
∵BC2+CD2=(2)2+()2=20+5=25,
∴BC2+CD2=BD2,∴∠BCD=90°.
16.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,则DE的长为 .
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠EAC=∠DAB.
易证△ACE≌△ABD(SAS).∴CE=BD.
(2)解:∵△ACE≌△ABD,∴DB=EC=4,
在Rt△ABC中,AB2+AC2=BC2,∴BC2=8.
在△DBC中,BC2+DC2=BD2,∴∠DCB=90°,
∴∠ACD=∠DCB+∠ACB=90°+45°=135°.
(3)【答案】2
17.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
(1)【证明】在△BCD和△FCE中,
∴△BCD≌△FCE(SAS).∴∠DBC=∠EFC.∴BD∥EF.
∵AF⊥EF,∴BD⊥AF.
(2)【解】由题意补全图形如图②.CD=CH.
证明:延长BC到F,使CF=BC,连接AF,EF,∵∠ACB=90°,∴AC⊥BF.
又∵BC=CF,∴AB=AF.由(1)可知BD∥EF,△BCD≌△FCE,则BD=EF,
∵AB2=AE2+BD2,∴AF2=AE2+EF2.∴∠AEF=90°.∴AE⊥EF.
∴BD⊥AE.∴∠DHE=90°.又∵CD=CE,∴CH=CD.
章末复习题
一、选择题
1.在直角三角形中,若勾为3,股为4,则弦为 ( )
A.5 B.6 C.7 D.8
2.在△ABC中,AB=,BC=,AC=,则 ( )
A.∠B+∠C=90° B.∠A+∠C=90°
C.∠A+∠B=90° D.∠B=∠C
3.下列命题的逆命题是真命题的是 ( )
A.如果两个角是直角,那么它们相等 B.全等三角形的面积相等
C.如果a>0,b>0,那么ab>0 D.两直线平行,内错角相等
4.下列定理中,没有逆定理的是 ( )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形两个锐角的和等于90°
5.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为 ( )
A. B. C.1 D.2
6.将长为8 cm的橡皮筋放置在水平桌面上,固定两端,然后把中点竖直向上拉升3 cm,则橡皮筋被拉长了 ( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10 m,BC=15 m,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要 ( )
A.75a元 B.50a元 C.a元 D.150a元
8.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
9.将一根25 cm长的细木棒放入长、宽、高分别为8 cm,6 cm,10 cm的长方体无盖盒子中,则细木棒在盒子外面的最短长度是 cm.
10.一个三角形的三边的比为5∶12∶13,它的周长为60 cm,则它的面积是 cm2.
11.有一长、宽、高分别为5 cm、4 cm、3 cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是 .
12.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕的△ABD折叠得到△AB'D,AB'与边BC交于点E,若△DEB'为直角三角形,则BD的长是 .
三、解答题
13.如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
14.下图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26 m,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1 m,AD=15 m,于是小敏大胆猜想立柱AB段的长为10 m,请判断小敏的猜想是否正确?如果正确,请写出理由,
如果错误,请求出立柱AB段的正确长度.
15.如图,每个小正方形的边长都为1.
(1)CD= ,BC= ;
(2)求四边形ABCD的面积与周长;
(3)求证:∠BCD=90°.
16.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,则DE的长为 .
17.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
5
参考答案
一、选择题
1.在直角三角形中,若勾为3,股为4,则弦为 ( A )
A.5 B.6 C.7 D.8
2.在△ABC中,AB=,BC=,AC=,则 ( A )
A.∠B+∠C=90° B.∠A+∠C=90°
C.∠A+∠B=90° D.∠B=∠C
3.下列命题的逆命题是真命题的是 ( D )
A.如果两个角是直角,那么它们相等 B.全等三角形的面积相等
C.如果a>0,b>0,那么ab>0 D.两直线平行,内错角相等
4.下列定理中,没有逆定理的是 ( B )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形两个锐角的和等于90°
5.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为 ( B )
A. B. C.1 D.2
6.将长为8 cm的橡皮筋放置在水平桌面上,固定两端,然后把中点竖直向上拉升3 cm,则橡皮筋被拉长了 ( A )
A.2 cm B.3 cm C.4 cm D.5 cm
7.为了打造“绿洲”,计划在市内一块如图所示的三角形空地上种植某种草皮,已知AB=10 m,BC=15 m,∠B=120°,这种草皮每平方米售价2a元,则购买这种草皮需要 ( A )
A.75a元 B.50a元 C.a元 D.150a元
8.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( C )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
9.将一根25 cm长的细木棒放入长、宽、高分别为8 cm,6 cm,10 cm的长方体无盖盒子中,则细木棒在盒子外面的最短长度是 cm.
【答案】5
10.一个三角形的三边的比为5∶12∶13,它的周长为60 cm,则它的面积是 cm2.
【答案】120
11.有一长、宽、高分别为5 cm、4 cm、3 cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是 .
【答案】5 cm
12.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕的△ABD折叠得到△AB'D,AB'与边BC交于点E,若△DEB'为直角三角形,则BD的长是 .
【答案】2或5
三、解答题
13.如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,D在同一条直线上,连接BE,求BE的长.
解:过点E作EF⊥BD,垂足为点F.
∵△DCE为等边三角形,
∴EF是△DCE的中线,
∴CF=CD=1.∴BF=BC+CF=2+1=3.
在Rt△EFC中,由勾股定理,得
EF2=EC2-CF2=22-12=3.
在Rt△EFB中,由勾股定理,得
BE2=BF2+EF2=32+3=12,∴BE=2.
14.下图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26 m,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1 m,AD=15 m,于是小敏大胆猜想立柱AB段的长为10 m,请判断小敏的猜想是否正确?如果正确,请写出理由,
如果错误,请求出立柱AB段的正确长度.
解:错误.延长FC交AB于点G,则CG⊥AB,
AG=CD=1 m,
GC=AD=15 m,
设BG=x m,则BC=(26-1-x)m,
在Rt△BGC中,∵BG2+CG2=CB2,
∴x2+152=(26-1-x)2,解得x=8,
∴BA=BG+GA=8+1=9(m),
∴小敏的猜想错误,立柱AB段的正确长度为9 m.
15.如图,每个小正方形的边长都为1.
(1)CD= ,BC= ;
【答案】 2
(2)求四边形ABCD的面积与周长;
(3)求证:∠BCD=90°.
(2)解:∵AB=5,AD==,
∴四边形ABCD的周长为
2++5+=+3+5,
∴S四边形ABCD=4×5-×2×4-×1×2- ×1×3-1×1=12.5.
(3)证明:连接BD,则BD2=32+42=25.
∵BC2+CD2=(2)2+()2=20+5=25,
∴BC2+CD2=BD2,∴∠BCD=90°.
16.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,则DE的长为 .
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠EAC=∠DAB.
易证△ACE≌△ABD(SAS).∴CE=BD.
(2)解:∵△ACE≌△ABD,∴DB=EC=4,
在Rt△ABC中,AB2+AC2=BC2,∴BC2=8.
在△DBC中,BC2+DC2=BD2,∴∠DCB=90°,
∴∠ACD=∠DCB+∠ACB=90°+45°=135°.
(3)【答案】2
17.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
(1)【证明】在△BCD和△FCE中,
∴△BCD≌△FCE(SAS).∴∠DBC=∠EFC.∴BD∥EF.
∵AF⊥EF,∴BD⊥AF.
(2)【解】由题意补全图形如图②.CD=CH.
证明:延长BC到F,使CF=BC,连接AF,EF,∵∠ACB=90°,∴AC⊥BF.
又∵BC=CF,∴AB=AF.由(1)可知BD∥EF,△BCD≌△FCE,则BD=EF,
∵AB2=AE2+BD2,∴AF2=AE2+EF2.∴∠AEF=90°.∴AE⊥EF.
∴BD⊥AE.∴∠DHE=90°.又∵CD=CE,∴CH=CD.
