17.2.1 勾股定理的逆定理 同步练习(含答案)
文档属性
| 名称 | 17.2.1 勾股定理的逆定理 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 09:23:03 | ||
图片预览




文档简介
17.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、选择题
1.已知三角形的三条边分别为a,b,c,则下列不能判断三角形为直角三角形的是( )
A.a2=-b2-c2 B.a2+b2=c2 C.a2-b2=c2 D.-a2-b2=-
2.下列各组数中能作为直角三角形的三边长的是( )
A.1,2,3 B.4,5, C.,, D.6,8,12
3.满足下述条件的三角形中,不是直角三角形的是( )
A.三条边长之比为1∶∶ B.三条边长分别为1,,2
C.三个内角之比为3∶4∶5 D.两个内角分别为40°和50°
4.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.如果ab=1,那么a=2+,b=2-
C.若a=b,则|a|=|b|
D.若a>b,则a2>b2
5.下列各定理中有逆定理的是( )
A.两直线平行,同位角相等
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
6.下列各组数中,不是勾股数的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
7.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( )
(1)a=,b=,c=;(2)a2=(b+c)(b-c);(3)∠A∶∠B∶∠C=1∶2∶3;(4)a=9,b=12,c=15;(5)a=2,b=3,c=4.
A.2个 B.3个 C.4个 D.5个
8.如图,△ABC中,AB=1,BC=2,AC=,AD是BC边上的中线,则AD的长度为( )
A.1 B.2 C. D.
第8题图 第9题图 第10题图
9.如图,方格中的点A,B称为格点(网格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( )
A.3 B.4 C.5 D.6
10.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形( )
A.1个 B.2个 C.3个 D.4个
11.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( )
A.10 B.11 C.12 D.13
12.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
二、填空题
13.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
14.若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是 cm2.
15.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
16.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数.请你写出两组不同于以上所给出的基本勾股数: .
三、解答题
17.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两直线平行,同旁内角互补;
(2)如果两个角是邻补角,那么这两个角互补.
18.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=,b=2 ,c=;
(2)a=5,b=7,c=9;
(3)a=2,b=,c=;
(4)a=5,b=2 ,c=1.
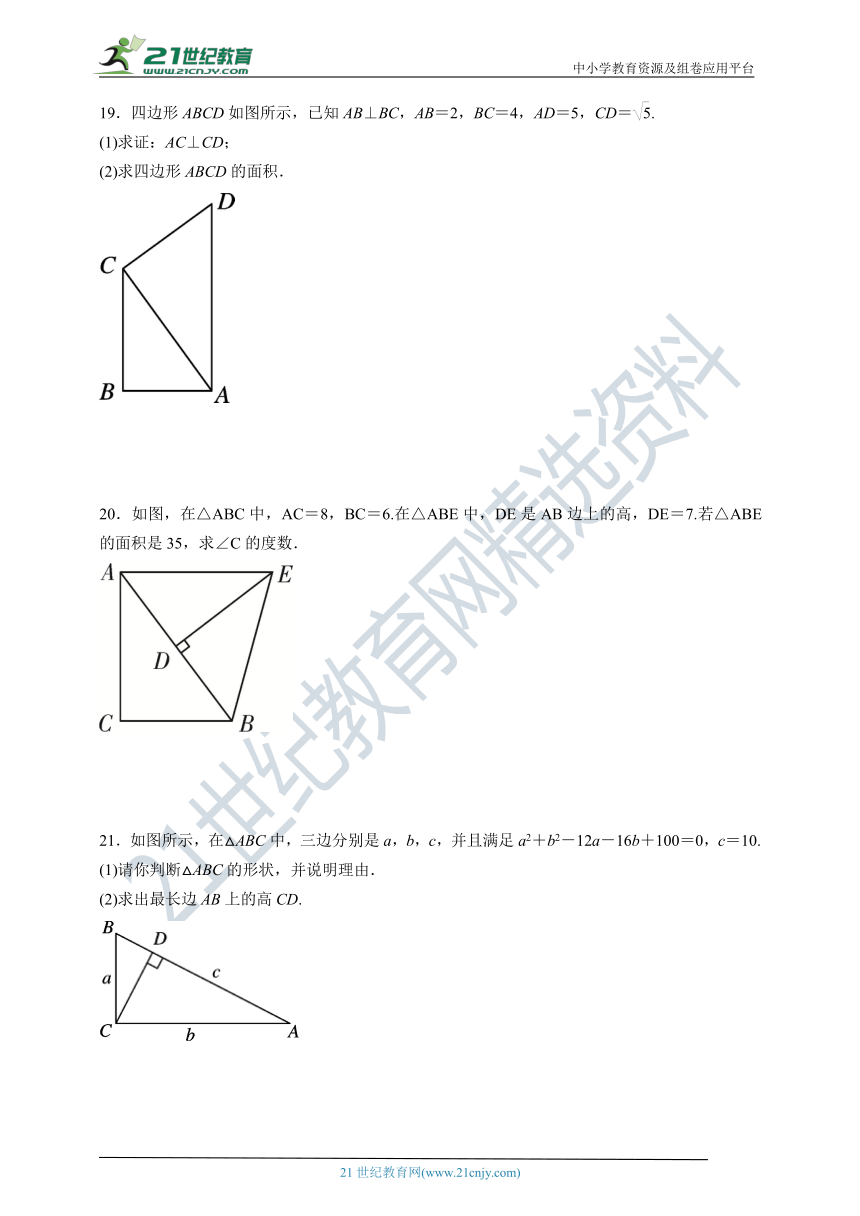
19.四边形ABCD如图所示,已知AB⊥BC,AB=2,BC=4,AD=5,CD=.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
20.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
21.如图所示,在△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
(1)请你判断△ABC的形状,并说明理由.
(2)求出最长边AB上的高CD.
22.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.已知三角形的三条边分别为a,b,c,则下列不能判断三角形为直角三角形的是( A )
A.a2=-b2-c2 B.a2+b2=c2 C.a2-b2=c2 D.-a2-b2=-
2.下列各组数中能作为直角三角形的三边长的是( B )
A.1,2,3 B.4,5, C.,, D.6,8,12
3.满足下述条件的三角形中,不是直角三角形的是( C )
A.三条边长之比为1∶∶ B.三条边长分别为1,,2
C.三个内角之比为3∶4∶5 D.两个内角分别为40°和50°
4.下列命题的逆命题成立的是( B )
A.全等三角形的对应角相等
B.如果ab=1,那么a=2+,b=2-
C.若a=b,则|a|=|b|
D.若a>b,则a2>b2
5.下列各定理中有逆定理的是( A )
A.两直线平行,同位角相等
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
6.下列各组数中,不是勾股数的是( D )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
7.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( B )
(1)a=,b=,c=;(2)a2=(b+c)(b-c);(3)∠A∶∠B∶∠C=1∶2∶3;(4)a=9,b=12,c=15;(5)a=2,b=3,c=4.
A.2个 B.3个 C.4个 D.5个
8.如图,△ABC中,AB=1,BC=2,AC=,AD是BC边上的中线,则AD的长度为( D )
A.1 B.2 C. D.
第8题图 第9题图 第10题图
9.如图,方格中的点A,B称为格点(网格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( B )
A.3 B.4 C.5 D.6
10.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形( D )
A.1个 B.2个 C.3个 D.4个
11.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( D )
A.10 B.11 C.12 D.13
12.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( C )
A.②④ B.①②④ C.①② D.①④
二、填空题
13.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
【答案】180
14.若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是 cm2.
【答案】150
15.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
【答案】等腰直角
16.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数.请你写出两组不同于以上所给出的基本勾股数: .
【答案】答案不唯一,如5,12,13;7,24,25
三、解答题
17.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两直线平行,同旁内角互补;
(2)如果两个角是邻补角,那么这两个角互补.
解:(1)两直线平行,同旁内角互补的逆命题是:同旁内角互补,两直线平行,成立.
(2)如果两个角是邻补角,那么这两个角互补的逆命题是:如果两个角互补,那么这两个角是邻补角,不成立.
18.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=,b=2 ,c=;
(2)a=5,b=7,c=9;
(3)a=2,b=,c=;
(4)a=5,b=2 ,c=1.
解:(1)是,∠B是直角.(2)不是.
(3)是,∠C是直角.(4)是,∠A是直角.
19.四边形ABCD如图所示,已知AB⊥BC,AB=2,BC=4,AD=5,CD=.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
解:(1)证明:在△ABC中,
∵AB⊥BC,AB=2,BC=4,
∴AC===2 ,
在△ACD中,∵AD=5,CD=,
∴AC2+CD2=(2 )2+()2=25=AD2,
∴∠ACD=90°,
∴AC⊥CD.
(2)∵△ABC的面积为×2×4=4,
△ACD的面积为×2 ×=5,
∴四边形ABCD的面积为4+5=9.
20.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
解:在△ABE中,
DE为AB边上的高,DE=7,
∴S△ABE=·AB·DE=35.
∴AB=10.∵AC=8,BC=6,
∴AC2+BC2=64+36=100=AB2.
∴△ABC为直角三角形.∴∠C=90°.
21.如图所示,在△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
(1)请你判断△ABC的形状,并说明理由.
(2)求出最长边AB上的高CD.
解:(1)△ABC为直角三角形,理由如下:
∵a2+b2-12a-16b+100=0,
∴(a-6)2+(b-8)2=0.
∴a=6,b=8.
∵a2+b2=62+82=100=102=c2,
∴△ABC为直角三角形,且∠ACB=90°.
(2)∵S△ABC=AC·BC=AB·CD,
即ab=c·CD,
∴CD===4.8.
22.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
解:(1)∵17=42+12,15=42-12,
∴8,15,17是完美勾股数;
∵41=52+42,9=52-42,
∴9,40,41是完美勾股数.
(2)由勾股定理得7a-7+(150-30b)=16×15,∴a=.
由题意可知7a-7>0,150-30b>0,
∴a>1,0<b<5.∵a和b均为正整数,∴b的可能值为1,2,3,4.
当b=1时,a=,不是正整数,不合题意;
当b=2时,a=,不是正整数,不合题意;
当b=3时,a=,不是正整数,不合题意;
当b=4时,a=31,是正整数,
此时=,=.
∵()2+()2=240,(4)2=240,
∴()2+()2=(4)2,
∴b=4符合题意.即a=31,b=4.
第1课时 勾股定理的逆定理
一、选择题
1.已知三角形的三条边分别为a,b,c,则下列不能判断三角形为直角三角形的是( )
A.a2=-b2-c2 B.a2+b2=c2 C.a2-b2=c2 D.-a2-b2=-
2.下列各组数中能作为直角三角形的三边长的是( )
A.1,2,3 B.4,5, C.,, D.6,8,12
3.满足下述条件的三角形中,不是直角三角形的是( )
A.三条边长之比为1∶∶ B.三条边长分别为1,,2
C.三个内角之比为3∶4∶5 D.两个内角分别为40°和50°
4.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.如果ab=1,那么a=2+,b=2-
C.若a=b,则|a|=|b|
D.若a>b,则a2>b2
5.下列各定理中有逆定理的是( )
A.两直线平行,同位角相等
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
6.下列各组数中,不是勾股数的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
7.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( )
(1)a=,b=,c=;(2)a2=(b+c)(b-c);(3)∠A∶∠B∶∠C=1∶2∶3;(4)a=9,b=12,c=15;(5)a=2,b=3,c=4.
A.2个 B.3个 C.4个 D.5个
8.如图,△ABC中,AB=1,BC=2,AC=,AD是BC边上的中线,则AD的长度为( )
A.1 B.2 C. D.
第8题图 第9题图 第10题图
9.如图,方格中的点A,B称为格点(网格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( )
A.3 B.4 C.5 D.6
10.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形( )
A.1个 B.2个 C.3个 D.4个
11.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( )
A.10 B.11 C.12 D.13
12.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
二、填空题
13.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
14.若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是 cm2.
15.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
16.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数.请你写出两组不同于以上所给出的基本勾股数: .
三、解答题
17.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两直线平行,同旁内角互补;
(2)如果两个角是邻补角,那么这两个角互补.
18.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=,b=2 ,c=;
(2)a=5,b=7,c=9;
(3)a=2,b=,c=;
(4)a=5,b=2 ,c=1.
19.四边形ABCD如图所示,已知AB⊥BC,AB=2,BC=4,AD=5,CD=.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
20.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
21.如图所示,在△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
(1)请你判断△ABC的形状,并说明理由.
(2)求出最长边AB上的高CD.
22.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.已知三角形的三条边分别为a,b,c,则下列不能判断三角形为直角三角形的是( A )
A.a2=-b2-c2 B.a2+b2=c2 C.a2-b2=c2 D.-a2-b2=-
2.下列各组数中能作为直角三角形的三边长的是( B )
A.1,2,3 B.4,5, C.,, D.6,8,12
3.满足下述条件的三角形中,不是直角三角形的是( C )
A.三条边长之比为1∶∶ B.三条边长分别为1,,2
C.三个内角之比为3∶4∶5 D.两个内角分别为40°和50°
4.下列命题的逆命题成立的是( B )
A.全等三角形的对应角相等
B.如果ab=1,那么a=2+,b=2-
C.若a=b,则|a|=|b|
D.若a>b,则a2>b2
5.下列各定理中有逆定理的是( A )
A.两直线平行,同位角相等
B.若两个数相等,则这两个数的绝对值也相等
C.对顶角相等
D.如果a=b,那么a2=b2
6.下列各组数中,不是勾股数的是( D )
A.3,4,5 B.6,8,10 C.7,24,25 D.4,5,6
7.已知a,b,c分别为△ABC的三边长,则符合下列条件的△ABC中,直角三角形有( B )
(1)a=,b=,c=;(2)a2=(b+c)(b-c);(3)∠A∶∠B∶∠C=1∶2∶3;(4)a=9,b=12,c=15;(5)a=2,b=3,c=4.
A.2个 B.3个 C.4个 D.5个
8.如图,△ABC中,AB=1,BC=2,AC=,AD是BC边上的中线,则AD的长度为( D )
A.1 B.2 C. D.
第8题图 第9题图 第10题图
9.如图,方格中的点A,B称为格点(网格线的交点),以AB为一边画△ABC,其中是直角三角形的格点C的个数为( B )
A.3 B.4 C.5 D.6
10.如图,在正方形ABCD中,AB=4,取AE=2,DF=1.图中共有直角三角形( D )
A.1个 B.2个 C.3个 D.4个
11.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( D )
A.10 B.11 C.12 D.13
12.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( C )
A.②④ B.①②④ C.①② D.①④
二、填空题
13.已知△ABC的三边长分别为9,40,41,则△ABC的面积为 .
【答案】180
14.若一个三角形三边的长度之比为3∶4∶5,且周长为60 cm,则它的面积是 cm2.
【答案】150
15.已知三角形的三边长之比为1∶1∶,则此三角形一定是 三角形.
【答案】等腰直角
16.将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数.请你写出两组不同于以上所给出的基本勾股数: .
【答案】答案不唯一,如5,12,13;7,24,25
三、解答题
17.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两直线平行,同旁内角互补;
(2)如果两个角是邻补角,那么这两个角互补.
解:(1)两直线平行,同旁内角互补的逆命题是:同旁内角互补,两直线平行,成立.
(2)如果两个角是邻补角,那么这两个角互补的逆命题是:如果两个角互补,那么这两个角是邻补角,不成立.
18.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=,b=2 ,c=;
(2)a=5,b=7,c=9;
(3)a=2,b=,c=;
(4)a=5,b=2 ,c=1.
解:(1)是,∠B是直角.(2)不是.
(3)是,∠C是直角.(4)是,∠A是直角.
19.四边形ABCD如图所示,已知AB⊥BC,AB=2,BC=4,AD=5,CD=.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
解:(1)证明:在△ABC中,
∵AB⊥BC,AB=2,BC=4,
∴AC===2 ,
在△ACD中,∵AD=5,CD=,
∴AC2+CD2=(2 )2+()2=25=AD2,
∴∠ACD=90°,
∴AC⊥CD.
(2)∵△ABC的面积为×2×4=4,
△ACD的面积为×2 ×=5,
∴四边形ABCD的面积为4+5=9.
20.如图,在△ABC中,AC=8,BC=6.在△ABE中,DE是AB边上的高,DE=7.若△ABE的面积是35,求∠C的度数.
解:在△ABE中,
DE为AB边上的高,DE=7,
∴S△ABE=·AB·DE=35.
∴AB=10.∵AC=8,BC=6,
∴AC2+BC2=64+36=100=AB2.
∴△ABC为直角三角形.∴∠C=90°.
21.如图所示,在△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
(1)请你判断△ABC的形状,并说明理由.
(2)求出最长边AB上的高CD.
解:(1)△ABC为直角三角形,理由如下:
∵a2+b2-12a-16b+100=0,
∴(a-6)2+(b-8)2=0.
∴a=6,b=8.
∵a2+b2=62+82=100=102=c2,
∴△ABC为直角三角形,且∠ACB=90°.
(2)∵S△ABC=AC·BC=AB·CD,
即ab=c·CD,
∴CD===4.8.
22.(1)小欢在研究勾股数时发现,某些正整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差,我们把这样的勾股数叫做完美勾股数.如3,4,5中,5=22+12,3=22-12;5,12,13中,13=32+22,5=32-22.判断8,15,17和9,40,41这两组勾股数是不是完美勾股数,并说明理由;
(2)有一个直角三角形两直角边长分别为和,斜边长为4,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值.
解:(1)∵17=42+12,15=42-12,
∴8,15,17是完美勾股数;
∵41=52+42,9=52-42,
∴9,40,41是完美勾股数.
(2)由勾股定理得7a-7+(150-30b)=16×15,∴a=.
由题意可知7a-7>0,150-30b>0,
∴a>1,0<b<5.∵a和b均为正整数,∴b的可能值为1,2,3,4.
当b=1时,a=,不是正整数,不合题意;
当b=2时,a=,不是正整数,不合题意;
当b=3时,a=,不是正整数,不合题意;
当b=4时,a=31,是正整数,
此时=,=.
∵()2+()2=240,(4)2=240,
∴()2+()2=(4)2,
∴b=4符合题意.即a=31,b=4.
