第17章 勾股定理 测试卷(含答案)
图片预览




文档简介
第17章 勾股定理 测试卷
(考试时间:100分钟,赋分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.已知a=1,c=,则b的值为( )
A. B.2 C. D.6
2.下列几组数:①7,24,25;②13,14,15;③60,80,100;④0.3,0.4,0.5,是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
3.已知Rt△ABC中,∠C=90°,∠A=45°,BC=2 cm,则AB的长是( )
A.2 cm B.2 cm C.2 cm D.4 cm
4.以下命题的逆命题是假命题的是( )
A.邻补角互补 B.直角三角形中两锐角互余
C.等腰三角形的两底角相等 D.线段垂直平分线上的点到线段两端点的距离相等
5.已知平面直角坐标系内点P(1,2),Q(2,-3),那么线段PQ的长等于( )
A.5 B. C. D.2
6.已知 A,B,C三地两两的距离如图所示,B地在A地的正西方向,下面说法不正确的是( )
A.C地在B地的正北方向上 B.A地在B地的正东方向上
C.C地在A地的北偏西60°方向上 D.A地在C地的南偏东30°方向上
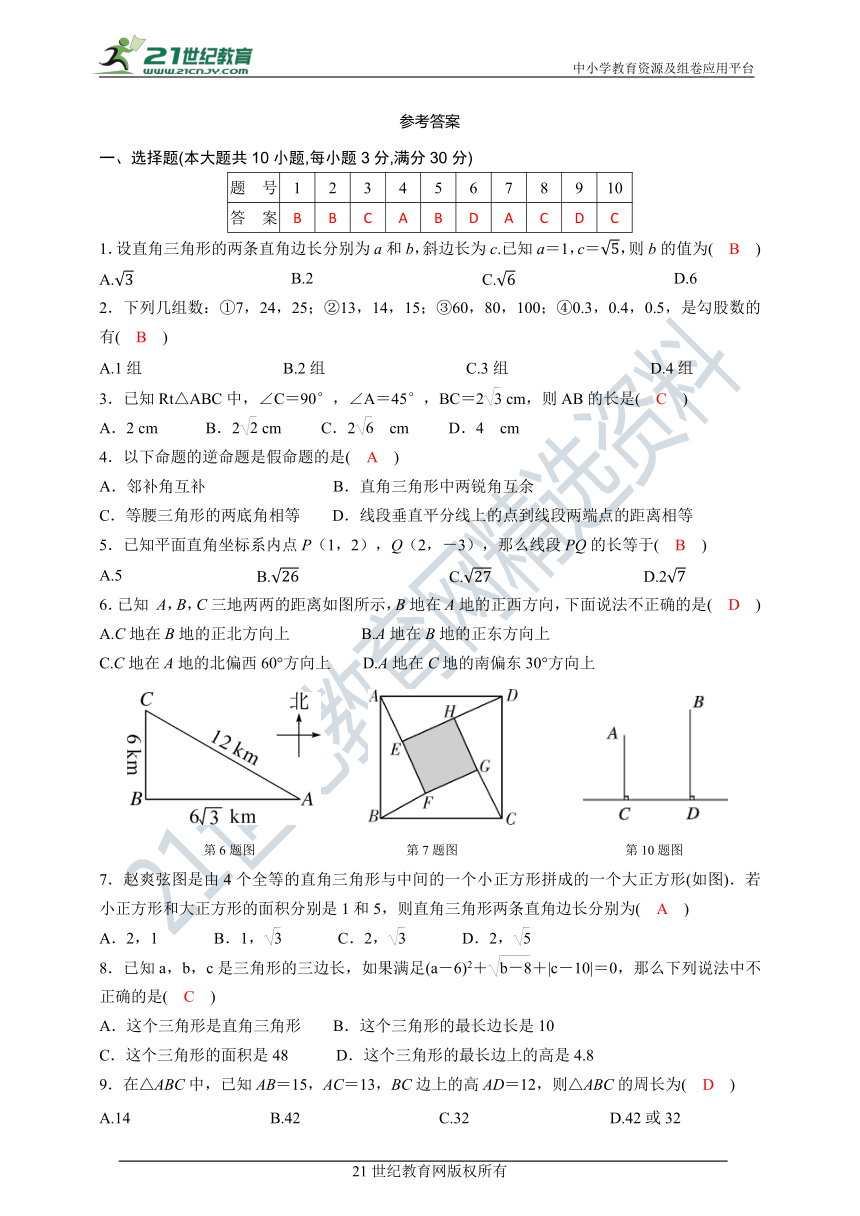
第6题图 第7题图 第10题图
7.赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( )
A.2,1 B.1, C.2, D.2,
8.已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
9.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )
A.14 B.42 C.32 D.42或32
10.如图,在一条公路CD的同一侧有A,B两个村庄,A,B与公路的距离AC,BD分别为500m和700m,且C,D两地相距500m.若要在公路旁(CD上)建一个车站,则A,B两村庄到车站的距离之和最短是( )
A.1000m B.1200m C.1300m D.1700m
二、填空题(本大题共8小题,每小题3分,满分24分)
11.命题“如果|a|=|b|,那么a=b”的逆命题是 .
12.在Rt△ABC中,斜边AB=a,则AB2+BC2+AC2= ____.
13.如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm)计算两圆孔中心A和B的距离为____mm.
第13题图 第14题图
14.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4,5,9,则△ABC____直角三角形.(选填“是”或“不是”)
15.现将一支长20 cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8 cm,6 cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
16.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
第16题图 第17题图 第18题图
17.如图,∠C=90°,△ABC的面积为20,在AB的同侧,分别以AB,BC,AC为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为____.
18.如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为 .
三、解答题(共66分)
19.(8分)一个零件的形状如图所示,按规定,这个零件中∠A和∠BDC都应为直角,工人师傅量得零件各边尺寸:AD=4,AB=3,BD=5,DC=12,BC=13,这个零件符合要求吗?为什么?
20.(8分)已知△ABC的三边长分别为a,b,c,且满足a+b=4,ab=1,c=,求证:△ABC为直角三角形.
21.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源,为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为13.5 km,如图,早上8:00甲先出发,他以6 km/h的速度向东行走,1 h后乙出发,他以5 km/h的速度向北行走,上午10:00,甲步行到A,乙步行到B.
(1)求甲、乙二人相距多远?(2)甲、乙二人是否能保持联系?
22.(10分)如图,某小区的两个喷泉A,B位于小路AC的同侧,两个喷泉的距离AB的长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)直接写出喷泉B到小路AC的距离.
23.(10分)定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图,若PB=PC,则P为△ABC的准外心.
已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上.求PA的长.
24.(10分)在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2;若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥CB于点D,设CD=x.
在Rt△ADC中,AD2=b2-x2;在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,即a2+b2=c2+2ax.
∵a>0,x>0,∴2ax>0.∴a2+b2>c2.
∴当△ABC为锐角三角形时,a2+b2>c2.
故小明的猜想是正确的.
请你猜想,当△ABC为钝角三角形时,如图③,a2+b2与c2的大小关系,并证明你猜想的结论.
25.(12分)在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第4页 共4页
参考答案
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 B B C A B D A C D C
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.已知a=1,c=,则b的值为( B )
A. B.2 C. D.6
2.下列几组数:①7,24,25;②13,14,15;③60,80,100;④0.3,0.4,0.5,是勾股数的有( B )
A.1组 B.2组 C.3组 D.4组
3.已知Rt△ABC中,∠C=90°,∠A=45°,BC=2 cm,则AB的长是( C )
A.2 cm B.2 cm C.2 cm D.4 cm
4.以下命题的逆命题是假命题的是( A )
A.邻补角互补 B.直角三角形中两锐角互余
C.等腰三角形的两底角相等 D.线段垂直平分线上的点到线段两端点的距离相等
5.已知平面直角坐标系内点P(1,2),Q(2,-3),那么线段PQ的长等于( B )
A.5 B. C. D.2
6.已知 A,B,C三地两两的距离如图所示,B地在A地的正西方向,下面说法不正确的是( D )
A.C地在B地的正北方向上 B.A地在B地的正东方向上
C.C地在A地的北偏西60°方向上 D.A地在C地的南偏东30°方向上
第6题图 第7题图 第10题图
7.赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( A )
A.2,1 B.1, C.2, D.2,
8.已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,那么下列说法中不正确的是( C )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
9.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( D )
A.14 B.42 C.32 D.42或32
10.如图,在一条公路CD的同一侧有A,B两个村庄,A,B与公路的距离AC,BD分别为500m和700m,且C,D两地相距500m.若要在公路旁(CD上)建一个车站,则A,B两村庄到车站的距离之和最短是( C )
A.1000m B.1200m C.1300m D.1700m
二、填空题(本大题共8小题,每小题3分,满分24分)
11.命题“如果|a|=|b|,那么a=b”的逆命题是 .
【答案】如果a=b,那么|a|=|b|
12.在Rt△ABC中,斜边AB=a,则AB2+BC2+AC2= ____.
【答案】2a2
13.如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm)计算两圆孔中心A和B的距离为____mm.
【答案】150
第13题图 第14题图
14.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4,5,9,则△ABC____直角三角形.(选填“是”或“不是”)
【答案】是
15.现将一支长20 cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8 cm,6 cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
【答案】10
16.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
【答案】-2
第16题图 第17题图 第18题图
17.如图,∠C=90°,△ABC的面积为20,在AB的同侧,分别以AB,BC,AC为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为____.
【答案】20
18.如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为 .
【答案】5+5
三、解答题(共66分)
19.(8分)一个零件的形状如图所示,按规定,这个零件中∠A和∠BDC都应为直角,工人师傅量得零件各边尺寸:AD=4,AB=3,BD=5,DC=12,BC=13,这个零件符合要求吗?为什么?
解:这个零件符合要求.理由:在△ABD中,
AB2+AD2=32+42=25,BD2=52=25.∴AB2+AD2=BD2,
∴∠A=90°,同理可证∠CDB=90°,∴这个零件符合要求.
20.(8分)已知△ABC的三边长分别为a,b,c,且满足a+b=4,ab=1,c=,求证:△ABC为直角三角形.
证明:∵a+b=4,∴(a+b)2=42.
∴a2+2ab+b2=16.
∵ab=1,∴a2+b2=14.
∵c=,∴c2=14.∴a2+b2=c2.
∴△ABC为直角三角形.
21.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源,为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为13.5 km,如图,早上8:00甲先出发,他以6 km/h的速度向东行走,1 h后乙出发,他以5 km/h的速度向北行走,上午10:00,甲步行到A,乙步行到B.
(1)求甲、乙二人相距多远?(2)甲、乙二人是否能保持联系?
解:(1)由题意得OA=12 km,OB=5 km,
在Rt△OAB中,AB2=122+52=169,∴AB=13 km,
答:上午10:00时,甲、乙两人相距13 km.
(2)∵13.5>13,∴甲、乙两人还能保持联系.
22.(10分)如图,某小区的两个喷泉A,B位于小路AC的同侧,两个喷泉的距离AB的长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)直接写出喷泉B到小路AC的距离.
解:(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m).
在Rt△AMN中,AM===200(m).
∴供水点M到喷泉A,B需要铺设的管道总长为200+150=350(m).
(2)150 m
23.(10分)定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图,若PB=PC,则P为△ABC的准外心.
已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上.求PA的长.
解:∵BC=5,AB=3,∴AC===4.
①若PB=PC,设PA=x,则PB=4-x,
在Rt△APB中,有x2+32=(4-x)2,解得x=,即PA=;
②若PA=PC,则PA=2;
③若PA=PB,由图知在Rt△PAB中不可能.综上可得PA=2或.
24.(10分)在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2;若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥CB于点D,设CD=x.
在Rt△ADC中,AD2=b2-x2;在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,即a2+b2=c2+2ax.
∵a>0,x>0,∴2ax>0.∴a2+b2>c2.
∴当△ABC为锐角三角形时,a2+b2>c2.
故小明的猜想是正确的.
请你猜想,当△ABC为钝角三角形时,如图③,a2+b2与c2的大小关系,并证明你猜想的结论.
【解】当△ABC为钝角三角形时,a2+b2与c2的大小关系为a2+b2<c2.
证明如下:如图③,过点A作AD⊥BC,交BC的延长线于点D.
设CD=y.在Rt△ADC中,由勾股定理得AD2=AC2-DC2=b2-y2;
在Rt△ADB中,由勾股定理得AD2=AB2-BD2=c2-(a+y)2.
∴b2-y2=c2-(a+y)2,整理,得a2+b2=c2-2ay.
∵a>0,y>0,∴2ay>0.∴a2+b2=c2-2ay<c2.∴当△ABC为钝角三角形时,a2+b2<c2.
25.(12分)在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
(1)【证明】在△BCD和△FCE中,
∴△BCD≌△FCE(SAS).∴∠DBC=∠EFC.∴BD∥EF.
∵AF⊥EF,∴BD⊥AF.
(2)【解】由题意补全图形如图②.CD=CH.
证明:延长BC到F,使CF=BC,连接AF,EF,∵∠ACB=90°,∴AC⊥BF.
又∵BC=CF,∴AB=AF.由(1)可知BD∥EF,△BCD≌△FCE,则BD=EF,
∵AB2=AE2+BD2,∴AF2=AE2+EF2.∴∠AEF=90°.∴AE⊥EF.
∴BD⊥AE.∴∠DHE=90°.又∵CD=CE,∴CH=CD.
21世纪教育网版权所有
(考试时间:100分钟,赋分:120分)
姓名:________ 班级:________ 分数:________
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.已知a=1,c=,则b的值为( )
A. B.2 C. D.6
2.下列几组数:①7,24,25;②13,14,15;③60,80,100;④0.3,0.4,0.5,是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
3.已知Rt△ABC中,∠C=90°,∠A=45°,BC=2 cm,则AB的长是( )
A.2 cm B.2 cm C.2 cm D.4 cm
4.以下命题的逆命题是假命题的是( )
A.邻补角互补 B.直角三角形中两锐角互余
C.等腰三角形的两底角相等 D.线段垂直平分线上的点到线段两端点的距离相等
5.已知平面直角坐标系内点P(1,2),Q(2,-3),那么线段PQ的长等于( )
A.5 B. C. D.2
6.已知 A,B,C三地两两的距离如图所示,B地在A地的正西方向,下面说法不正确的是( )
A.C地在B地的正北方向上 B.A地在B地的正东方向上
C.C地在A地的北偏西60°方向上 D.A地在C地的南偏东30°方向上
第6题图 第7题图 第10题图
7.赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( )
A.2,1 B.1, C.2, D.2,
8.已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,那么下列说法中不正确的是( )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
9.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( )
A.14 B.42 C.32 D.42或32
10.如图,在一条公路CD的同一侧有A,B两个村庄,A,B与公路的距离AC,BD分别为500m和700m,且C,D两地相距500m.若要在公路旁(CD上)建一个车站,则A,B两村庄到车站的距离之和最短是( )
A.1000m B.1200m C.1300m D.1700m
二、填空题(本大题共8小题,每小题3分,满分24分)
11.命题“如果|a|=|b|,那么a=b”的逆命题是 .
12.在Rt△ABC中,斜边AB=a,则AB2+BC2+AC2= ____.
13.如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm)计算两圆孔中心A和B的距离为____mm.
第13题图 第14题图
14.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4,5,9,则△ABC____直角三角形.(选填“是”或“不是”)
15.现将一支长20 cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8 cm,6 cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
16.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
第16题图 第17题图 第18题图
17.如图,∠C=90°,△ABC的面积为20,在AB的同侧,分别以AB,BC,AC为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为____.
18.如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为 .
三、解答题(共66分)
19.(8分)一个零件的形状如图所示,按规定,这个零件中∠A和∠BDC都应为直角,工人师傅量得零件各边尺寸:AD=4,AB=3,BD=5,DC=12,BC=13,这个零件符合要求吗?为什么?
20.(8分)已知△ABC的三边长分别为a,b,c,且满足a+b=4,ab=1,c=,求证:△ABC为直角三角形.
21.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源,为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为13.5 km,如图,早上8:00甲先出发,他以6 km/h的速度向东行走,1 h后乙出发,他以5 km/h的速度向北行走,上午10:00,甲步行到A,乙步行到B.
(1)求甲、乙二人相距多远?(2)甲、乙二人是否能保持联系?
22.(10分)如图,某小区的两个喷泉A,B位于小路AC的同侧,两个喷泉的距离AB的长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)直接写出喷泉B到小路AC的距离.
23.(10分)定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图,若PB=PC,则P为△ABC的准外心.
已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上.求PA的长.
24.(10分)在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2;若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥CB于点D,设CD=x.
在Rt△ADC中,AD2=b2-x2;在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,即a2+b2=c2+2ax.
∵a>0,x>0,∴2ax>0.∴a2+b2>c2.
∴当△ABC为锐角三角形时,a2+b2>c2.
故小明的猜想是正确的.
请你猜想,当△ABC为钝角三角形时,如图③,a2+b2与c2的大小关系,并证明你猜想的结论.
25.(12分)在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第4页 共4页
参考答案
一、选择题(本大题共10小题,每小题3分,满分30分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 B B C A B D A C D C
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.已知a=1,c=,则b的值为( B )
A. B.2 C. D.6
2.下列几组数:①7,24,25;②13,14,15;③60,80,100;④0.3,0.4,0.5,是勾股数的有( B )
A.1组 B.2组 C.3组 D.4组
3.已知Rt△ABC中,∠C=90°,∠A=45°,BC=2 cm,则AB的长是( C )
A.2 cm B.2 cm C.2 cm D.4 cm
4.以下命题的逆命题是假命题的是( A )
A.邻补角互补 B.直角三角形中两锐角互余
C.等腰三角形的两底角相等 D.线段垂直平分线上的点到线段两端点的距离相等
5.已知平面直角坐标系内点P(1,2),Q(2,-3),那么线段PQ的长等于( B )
A.5 B. C. D.2
6.已知 A,B,C三地两两的距离如图所示,B地在A地的正西方向,下面说法不正确的是( D )
A.C地在B地的正北方向上 B.A地在B地的正东方向上
C.C地在A地的北偏西60°方向上 D.A地在C地的南偏东30°方向上
第6题图 第7题图 第10题图
7.赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( A )
A.2,1 B.1, C.2, D.2,
8.已知a,b,c是三角形的三边长,如果满足(a-6)2++|c-10|=0,那么下列说法中不正确的是( C )
A.这个三角形是直角三角形 B.这个三角形的最长边长是10
C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.8
9.在△ABC中,已知AB=15,AC=13,BC边上的高AD=12,则△ABC的周长为( D )
A.14 B.42 C.32 D.42或32
10.如图,在一条公路CD的同一侧有A,B两个村庄,A,B与公路的距离AC,BD分别为500m和700m,且C,D两地相距500m.若要在公路旁(CD上)建一个车站,则A,B两村庄到车站的距离之和最短是( C )
A.1000m B.1200m C.1300m D.1700m
二、填空题(本大题共8小题,每小题3分,满分24分)
11.命题“如果|a|=|b|,那么a=b”的逆命题是 .
【答案】如果a=b,那么|a|=|b|
12.在Rt△ABC中,斜边AB=a,则AB2+BC2+AC2= ____.
【答案】2a2
13.如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm)计算两圆孔中心A和B的距离为____mm.
【答案】150
第13题图 第14题图
14.如图,分别以△ABC的三边为直径向外作3个半圆,它们的面积分别为4,5,9,则△ABC____直角三角形.(选填“是”或“不是”)
【答案】是
15.现将一支长20 cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8 cm,6 cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
【答案】10
16.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
【答案】-2
第16题图 第17题图 第18题图
17.如图,∠C=90°,△ABC的面积为20,在AB的同侧,分别以AB,BC,AC为直径作三个半圆,则阴影部分(即“希波克拉底月牙形”)的面积为____.
【答案】20
18.如图,已知∠BAC=60°,AD是角平分线且AD=10,作AD的垂直平分线交AC于点F,作DE⊥AC,则△DEF的周长为 .
【答案】5+5
三、解答题(共66分)
19.(8分)一个零件的形状如图所示,按规定,这个零件中∠A和∠BDC都应为直角,工人师傅量得零件各边尺寸:AD=4,AB=3,BD=5,DC=12,BC=13,这个零件符合要求吗?为什么?
解:这个零件符合要求.理由:在△ABD中,
AB2+AD2=32+42=25,BD2=52=25.∴AB2+AD2=BD2,
∴∠A=90°,同理可证∠CDB=90°,∴这个零件符合要求.
20.(8分)已知△ABC的三边长分别为a,b,c,且满足a+b=4,ab=1,c=,求证:△ABC为直角三角形.
证明:∵a+b=4,∴(a+b)2=42.
∴a2+2ab+b2=16.
∵ab=1,∴a2+b2=14.
∵c=,∴c2=14.∴a2+b2=c2.
∴△ABC为直角三角形.
21.(8分)甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源,为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为13.5 km,如图,早上8:00甲先出发,他以6 km/h的速度向东行走,1 h后乙出发,他以5 km/h的速度向北行走,上午10:00,甲步行到A,乙步行到B.
(1)求甲、乙二人相距多远?(2)甲、乙二人是否能保持联系?
解:(1)由题意得OA=12 km,OB=5 km,
在Rt△OAB中,AB2=122+52=169,∴AB=13 km,
答:上午10:00时,甲、乙两人相距13 km.
(2)∵13.5>13,∴甲、乙两人还能保持联系.
22.(10分)如图,某小区的两个喷泉A,B位于小路AC的同侧,两个喷泉的距离AB的长为250m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120m,BM的长为150m.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)直接写出喷泉B到小路AC的距离.
解:(1)在Rt△MNB中,BN===90(m),
∴AN=AB-BN=250-90=160(m).
在Rt△AMN中,AM===200(m).
∴供水点M到喷泉A,B需要铺设的管道总长为200+150=350(m).
(2)150 m
23.(10分)定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图,若PB=PC,则P为△ABC的准外心.
已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上.求PA的长.
解:∵BC=5,AB=3,∴AC===4.
①若PB=PC,设PA=x,则PB=4-x,
在Rt△APB中,有x2+32=(4-x)2,解得x=,即PA=;
②若PA=PC,则PA=2;
③若PA=PB,由图知在Rt△PAB中不可能.综上可得PA=2或.
24.(10分)在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2;若△ABC为锐角三角形,小明猜想:a2+b2>c2.理由如下:
如图②,过点A作AD⊥CB于点D,设CD=x.
在Rt△ADC中,AD2=b2-x2;在Rt△ADB中,AD2=c2-(a-x)2,
∴b2-x2=c2-(a-x)2,即a2+b2=c2+2ax.
∵a>0,x>0,∴2ax>0.∴a2+b2>c2.
∴当△ABC为锐角三角形时,a2+b2>c2.
故小明的猜想是正确的.
请你猜想,当△ABC为钝角三角形时,如图③,a2+b2与c2的大小关系,并证明你猜想的结论.
【解】当△ABC为钝角三角形时,a2+b2与c2的大小关系为a2+b2<c2.
证明如下:如图③,过点A作AD⊥BC,交BC的延长线于点D.
设CD=y.在Rt△ADC中,由勾股定理得AD2=AC2-DC2=b2-y2;
在Rt△ADB中,由勾股定理得AD2=AB2-BD2=c2-(a+y)2.
∴b2-y2=c2-(a+y)2,整理,得a2+b2=c2-2ay.
∵a>0,y>0,∴2ay>0.∴a2+b2=c2-2ay<c2.∴当△ABC为钝角三角形时,a2+b2<c2.
25.(12分)在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.
(1)如图①,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;
(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图②,若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.
(1)【证明】在△BCD和△FCE中,
∴△BCD≌△FCE(SAS).∴∠DBC=∠EFC.∴BD∥EF.
∵AF⊥EF,∴BD⊥AF.
(2)【解】由题意补全图形如图②.CD=CH.
证明:延长BC到F,使CF=BC,连接AF,EF,∵∠ACB=90°,∴AC⊥BF.
又∵BC=CF,∴AB=AF.由(1)可知BD∥EF,△BCD≌△FCE,则BD=EF,
∵AB2=AE2+BD2,∴AF2=AE2+EF2.∴∠AEF=90°.∴AE⊥EF.
∴BD⊥AE.∴∠DHE=90°.又∵CD=CE,∴CH=CD.
21世纪教育网版权所有
