第17章 勾股定理 专题训练 利用勾股定理解题的六种常见题型(含解析)
文档属性
| 名称 | 第17章 勾股定理 专题训练 利用勾股定理解题的六种常见题型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 09:15:03 | ||
图片预览


文档简介
第17章 勾股定理 专题训练
利用勾股定理解题的六种常见题型
【题型先知】
【专题训练】
题型1 利用勾股定理求线段长
类型1 求三角形中线段长
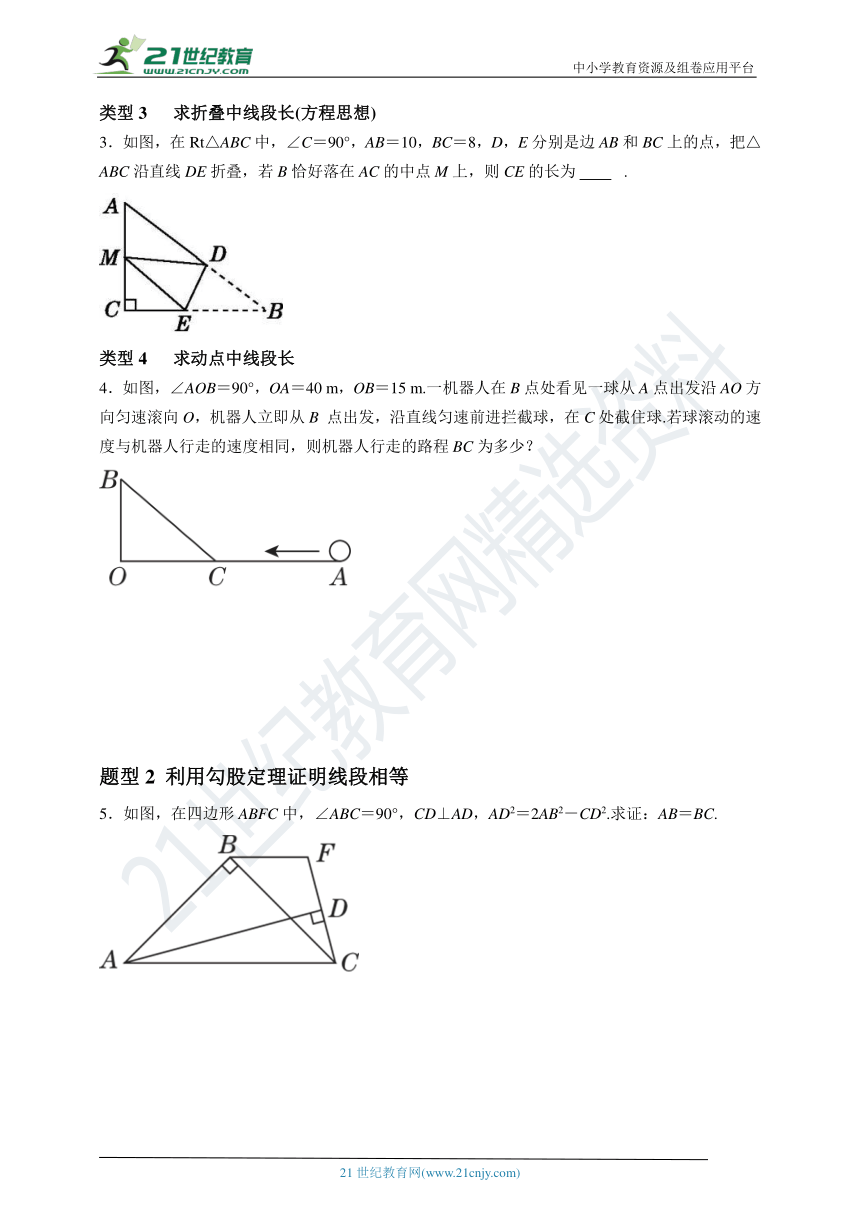
1.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,AC=6,BC=8,则DB的长为 .
类型2 求四边形中线段长
2.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32.求BC和CD的长度.
类型3 求折叠中线段长(方程思想)
3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,D,E分别是边AB和BC上的点,把△ABC沿直线DE折叠,若B恰好落在AC的中点M上,则CE的长为 .
类型4 求动点中线段长
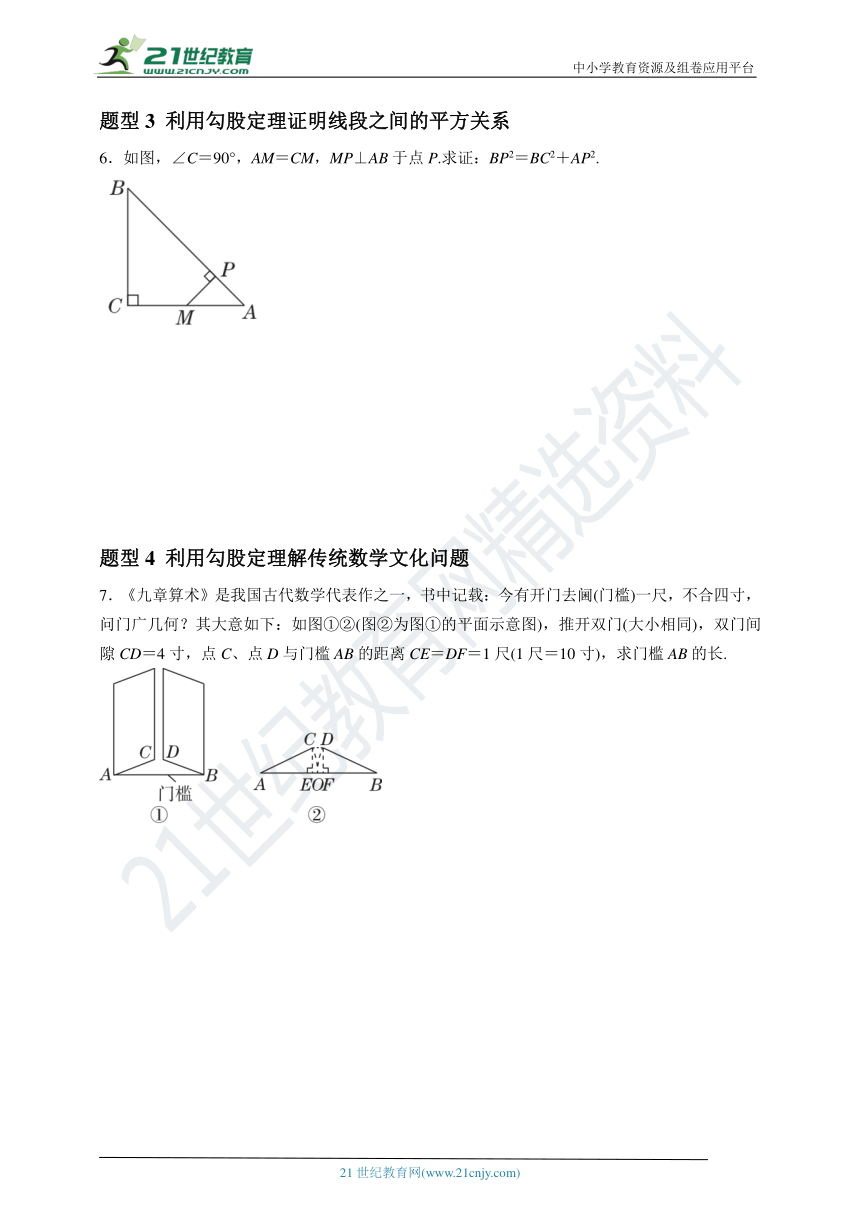
4.如图,∠AOB=90°,OA=40 m,OB=15 m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B 点出发,沿直线匀速前进拦截球,在C处截住球.若球滚动的速度与机器人行走的速度相同,则机器人行走的路程BC为多少?
题型2 利用勾股定理证明线段相等
5.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
题型3 利用勾股定理证明线段之间的平方关系
6.如图,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=BC2+AP2.
题型4 利用勾股定理解传统数学文化问题
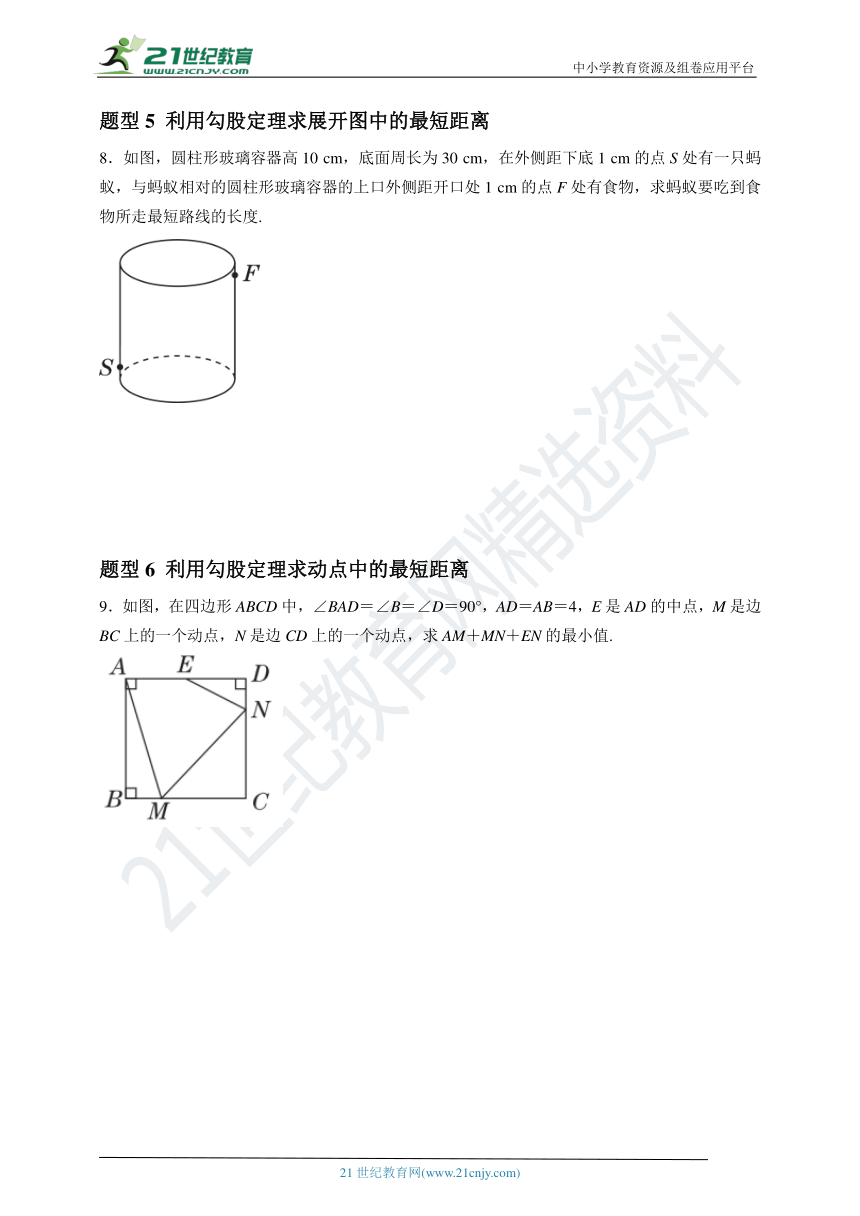
7.《九章算术》是我国古代数学代表作之一,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意如下:如图①②(图②为图①的平面示意图),推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求门槛AB的长.
题型5 利用勾股定理求展开图中的最短距离
8.如图,圆柱形玻璃容器高10 cm,底面周长为30 cm,在外侧距下底1 cm的点S处有一只蚂蚁,与蚂蚁相对的圆柱形玻璃容器的上口外侧距开口处1 cm的点F处有食物,求蚂蚁要吃到食物所走最短路线的长度.
题型6 利用勾股定理求动点中的最短距离
9.如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD的中点,M是边BC上的一个动点,N是边CD上的一个动点,求AM+MN+EN的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【专题训练】
题型1 利用勾股定理求线段长
类型1 求三角形中线段长
1.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,AC=6,BC=8,则DB的长为 .
【答案】5
【解析】利用勾股定理得AB=10,根据角平分线的性质得到DE=CD,利用HL证明Rt△AED≌Rt△ACD得到AE=AC=6,则BE=4,设BD=x,则CD=DE=8-x,最后利用勾股定理建立方程即可求解.
类型2 求四边形中线段长
2.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32.求BC和CD的长度.
【解】如图,连接BD.
∵AB=AD,∠A=60°,
∴△ABD为等边三角形.
∴∠1=60°,BD=AD=8.
又∵∠ADC=150°,∴∠2=90°.
设BC=x,则CD=32-8-8-x=16-x,
由勾股定理得x2=82+(16-x)2,
解得x=10.
∴BC=10,CD=6.
类型3 求折叠中线段长(方程思想)
3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,D,E分别是边AB和BC上的点,把△ABC沿直线DE折叠,若B恰好落在AC的中点M上,则CE的长为 .
【答案】
【解析】在Rt△ABC中,利用勾股定理求得AC=6,结合点M是AC的中点可得CM=3,由折叠可知ME=BE=BC-CE,设CE=x,则ME=8-x,在Rt△CME中运用勾股定理求解即可.
类型4 求动点中线段长
4.如图,∠AOB=90°,OA=40 m,OB=15 m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B 点出发,沿直线匀速前进拦截球,在C处截住球.若球滚动的速度与机器人行走的速度相同,则机器人行走的路程BC为多少?
【解】∵球滚动的速度与机器人行走的速度相同,
∴BC=AC.
设BC=AC=x m,则OC=(40-x)m,
在Rt△BOC中,∵OB2+OC2=BC2,
∴152+(40-x)2=x2,解得x=.
∴机器人行走的路程BC为 m.
题型2 利用勾股定理证明线段相等
5.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
【证明】∵CD⊥AD,
∴∠ADC=90°,即△ADC是直角三角形.
由勾股定理得AD2+CD2=AC2.
又∵AD2=2AB2-CD2,
∴AD2+CD2=2AB2.
∴AC2=2AB2.
∵∠ABC=90°,∴AB2+BC2=AC2.
∴AB2+BC2=2AB2.
∴BC2=AB2,即AB=BC.
题型3 利用勾股定理证明线段之间的平方关系
6.如图,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=BC2+AP2.
【证明】如图,连接BM.
∵PM⊥AB,∴△BMP和△AMP均为直角三角形.
∴BP2+PM2=BM2,AP2+PM2=AM2.
∵∠C=90°,∴△MBC为直角三角形.
∴BC2+CM2=BM2.
∴BP2+PM2=BC2+CM2.
又∵CM=AM,∴CM2=AM2=AP2+PM2.
∴BP2+PM2=BC2+AP2+PM2.
∴BP2=BC2+AP2.
题型4 利用勾股定理解传统数学文化问题
7.《九章算术》是我国古代数学代表作之一,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意如下:如图①②(图②为图①的平面示意图),推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求门槛AB的长.
【解】设AE=x寸,易知AC=AO=(x+2)寸,BF=x寸.∵AE2+CE2=AC2,
∴x2+102=(x+2)2,解得x=24.
∴AB=24+24+4=52(寸),
即门槛AB的长为52寸.
题型5 利用勾股定理求展开图中的最短距离
8.如图,圆柱形玻璃容器高10 cm,底面周长为30 cm,在外侧距下底1 cm的点S处有一只蚂蚁,与蚂蚁相对的圆柱形玻璃容器的上口外侧距开口处1 cm的点F处有食物,求蚂蚁要吃到食物所走最短路线的长度.
【解】如图,将圆柱形玻璃容器侧面展开,连接SF,过点S作SP⊥MN于点P.
由题意可知FP=10-2=8(cm),
SP=30÷2=15(cm).
在Rt△SPF中,SF====17(cm).
答:蚂蚁要吃到食物所走最短路线的长度为17 cm.
题型6 利用勾股定理求动点中的最短距离
9.如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD的中点,M是边BC上的一个动点,N是边CD上的一个动点,求AM+MN+EN的最小值.
【解】如图,作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,A1E1.
易知A,B,A1在一条直线上,A,D,E1在一条直线上.
∵点A和点A1关于BC对称,点E和点E1关于DC对称,
∴AB=A1B,AM=A1M,DE=DE1,EN=E1N,
∴AM+MN+EN=A1M+MN+E1N≥A1E1,
∴AM+MN+EN的最小值是A1E1的长.
∵AD=AB=4,E是AD的中点,
∴AB=A1B=4,ED=E1D=2,
∴AA1=8,AE1=6.
∵∠BAD=90°,
∴A1=62+82=102,
∴A1E1=10,即AM+MN+EN的最小值为10.
利用勾股定理解题的六种常见题型
【题型先知】
【专题训练】
题型1 利用勾股定理求线段长
类型1 求三角形中线段长
1.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,AC=6,BC=8,则DB的长为 .
类型2 求四边形中线段长
2.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32.求BC和CD的长度.
类型3 求折叠中线段长(方程思想)
3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,D,E分别是边AB和BC上的点,把△ABC沿直线DE折叠,若B恰好落在AC的中点M上,则CE的长为 .
类型4 求动点中线段长
4.如图,∠AOB=90°,OA=40 m,OB=15 m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B 点出发,沿直线匀速前进拦截球,在C处截住球.若球滚动的速度与机器人行走的速度相同,则机器人行走的路程BC为多少?
题型2 利用勾股定理证明线段相等
5.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
题型3 利用勾股定理证明线段之间的平方关系
6.如图,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=BC2+AP2.
题型4 利用勾股定理解传统数学文化问题
7.《九章算术》是我国古代数学代表作之一,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意如下:如图①②(图②为图①的平面示意图),推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求门槛AB的长.
题型5 利用勾股定理求展开图中的最短距离
8.如图,圆柱形玻璃容器高10 cm,底面周长为30 cm,在外侧距下底1 cm的点S处有一只蚂蚁,与蚂蚁相对的圆柱形玻璃容器的上口外侧距开口处1 cm的点F处有食物,求蚂蚁要吃到食物所走最短路线的长度.
题型6 利用勾股定理求动点中的最短距离
9.如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD的中点,M是边BC上的一个动点,N是边CD上的一个动点,求AM+MN+EN的最小值.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【专题训练】
题型1 利用勾股定理求线段长
类型1 求三角形中线段长
1.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,AC=6,BC=8,则DB的长为 .
【答案】5
【解析】利用勾股定理得AB=10,根据角平分线的性质得到DE=CD,利用HL证明Rt△AED≌Rt△ACD得到AE=AC=6,则BE=4,设BD=x,则CD=DE=8-x,最后利用勾股定理建立方程即可求解.
类型2 求四边形中线段长
2.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32.求BC和CD的长度.
【解】如图,连接BD.
∵AB=AD,∠A=60°,
∴△ABD为等边三角形.
∴∠1=60°,BD=AD=8.
又∵∠ADC=150°,∴∠2=90°.
设BC=x,则CD=32-8-8-x=16-x,
由勾股定理得x2=82+(16-x)2,
解得x=10.
∴BC=10,CD=6.
类型3 求折叠中线段长(方程思想)
3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,D,E分别是边AB和BC上的点,把△ABC沿直线DE折叠,若B恰好落在AC的中点M上,则CE的长为 .
【答案】
【解析】在Rt△ABC中,利用勾股定理求得AC=6,结合点M是AC的中点可得CM=3,由折叠可知ME=BE=BC-CE,设CE=x,则ME=8-x,在Rt△CME中运用勾股定理求解即可.
类型4 求动点中线段长
4.如图,∠AOB=90°,OA=40 m,OB=15 m.一机器人在B点处看见一球从A点出发沿AO方向匀速滚向O,机器人立即从B 点出发,沿直线匀速前进拦截球,在C处截住球.若球滚动的速度与机器人行走的速度相同,则机器人行走的路程BC为多少?
【解】∵球滚动的速度与机器人行走的速度相同,
∴BC=AC.
设BC=AC=x m,则OC=(40-x)m,
在Rt△BOC中,∵OB2+OC2=BC2,
∴152+(40-x)2=x2,解得x=.
∴机器人行走的路程BC为 m.
题型2 利用勾股定理证明线段相等
5.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
【证明】∵CD⊥AD,
∴∠ADC=90°,即△ADC是直角三角形.
由勾股定理得AD2+CD2=AC2.
又∵AD2=2AB2-CD2,
∴AD2+CD2=2AB2.
∴AC2=2AB2.
∵∠ABC=90°,∴AB2+BC2=AC2.
∴AB2+BC2=2AB2.
∴BC2=AB2,即AB=BC.
题型3 利用勾股定理证明线段之间的平方关系
6.如图,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=BC2+AP2.
【证明】如图,连接BM.
∵PM⊥AB,∴△BMP和△AMP均为直角三角形.
∴BP2+PM2=BM2,AP2+PM2=AM2.
∵∠C=90°,∴△MBC为直角三角形.
∴BC2+CM2=BM2.
∴BP2+PM2=BC2+CM2.
又∵CM=AM,∴CM2=AM2=AP2+PM2.
∴BP2+PM2=BC2+AP2+PM2.
∴BP2=BC2+AP2.
题型4 利用勾股定理解传统数学文化问题
7.《九章算术》是我国古代数学代表作之一,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意如下:如图①②(图②为图①的平面示意图),推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求门槛AB的长.
【解】设AE=x寸,易知AC=AO=(x+2)寸,BF=x寸.∵AE2+CE2=AC2,
∴x2+102=(x+2)2,解得x=24.
∴AB=24+24+4=52(寸),
即门槛AB的长为52寸.
题型5 利用勾股定理求展开图中的最短距离
8.如图,圆柱形玻璃容器高10 cm,底面周长为30 cm,在外侧距下底1 cm的点S处有一只蚂蚁,与蚂蚁相对的圆柱形玻璃容器的上口外侧距开口处1 cm的点F处有食物,求蚂蚁要吃到食物所走最短路线的长度.
【解】如图,将圆柱形玻璃容器侧面展开,连接SF,过点S作SP⊥MN于点P.
由题意可知FP=10-2=8(cm),
SP=30÷2=15(cm).
在Rt△SPF中,SF====17(cm).
答:蚂蚁要吃到食物所走最短路线的长度为17 cm.
题型6 利用勾股定理求动点中的最短距离
9.如图,在四边形ABCD中,∠BAD=∠B=∠D=90°,AD=AB=4,E是AD的中点,M是边BC上的一个动点,N是边CD上的一个动点,求AM+MN+EN的最小值.
【解】如图,作A点关于BC的对称点A1,连接A1M,作E点关于DC的对称点E1,连接E1N,A1E1.
易知A,B,A1在一条直线上,A,D,E1在一条直线上.
∵点A和点A1关于BC对称,点E和点E1关于DC对称,
∴AB=A1B,AM=A1M,DE=DE1,EN=E1N,
∴AM+MN+EN=A1M+MN+E1N≥A1E1,
∴AM+MN+EN的最小值是A1E1的长.
∵AD=AB=4,E是AD的中点,
∴AB=A1B=4,ED=E1D=2,
∴AA1=8,AE1=6.
∵∠BAD=90°,
∴A1=62+82=102,
∴A1E1=10,即AM+MN+EN的最小值为10.
