17.2.2 勾股定理及其逆定理的综合应用 同步练习(含答案)
文档属性
| 名称 | 17.2.2 勾股定理及其逆定理的综合应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 09:28:14 | ||
图片预览




文档简介
17.2 勾股定理的逆定理
第2课时 勾股定理及其逆定理的综合应用
一、选择题
1.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( )
A.正东或正西 B.正南 C.正北 D.正南或正北
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列选项中正确的是( )
A B C D
3.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
第3题图 第5题图 第6题图
4.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点.则线段BP长的最小值是( )
A. B.5 C. D.12
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( )
A.30° B.42° C.45° D.50°
二、填空题
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
8.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
三、解答题
10.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,
那么种植这块三角形空地需要多少钱?
11.如图,在公路的同侧有A,B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8 km,BC=15 km,AB=17 km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5 km/h,问多长时间后这人距离B送奶站最近.
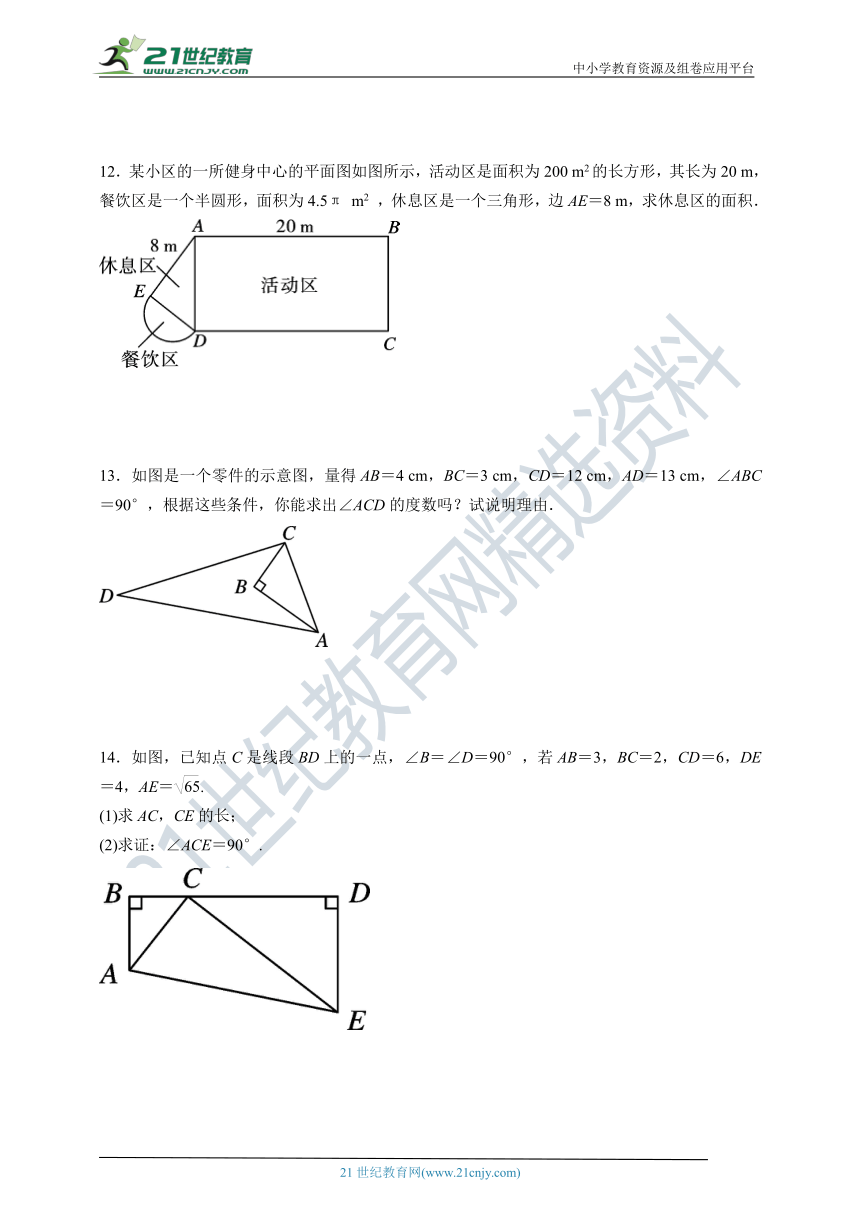
12.某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2 ,休息区是一个三角形,边AE=8 m,求休息区的面积.
13.如图是一个零件的示意图,量得AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
14.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=.
(1)求AC,CE的长;
(2)求证:∠ACE=90°.
15.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.
(1)求∠BAD的度数;
(2)求四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
16.阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
17.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边的平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? (填“是”或“不是”);
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据;
(3)在Rt△ABC中,三边长分别为a,b,c,且a2=50,c2=100,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a.若Rt△ABC是奇异三角形,求a2∶b2∶c2.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( D )
A.正东或正西 B.正南 C.正北 D.正南或正北
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列选项中正确的是( C )
A B C D
3.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( A )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
第3题图 第5题图 第6题图
4.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点.则线段BP长的最小值是( A )
A. B.5 C. D.12
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( C )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( C )
A.30° B.42° C.45° D.50°
【解析】连接AC,AD,如图,根据勾股定理可得AD=AC=BC=,CD=,∴∠ABC=∠BAC,在△ACD中,AD2+AC2=()2+()2=10,CD2=()2=10,∴AD2+AC2=CD2,∴△ACD是直角三角形,∠DAC=90°,∵AD=CD,∴△ACD是等腰直角三角形,∴∠ACD=45°,∵AB∥EC,∴∠BAC=∠ACE,∴∠ABC-∠DCE=∠BAC-∠DCE=∠ACE-∠DCE=∠ACD=45°.
二、填空题
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
【答案】13,84,85
8.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
【答案】24
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
【答案】
三、解答题
10.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,
那么种植这块三角形空地需要多少钱?
解:∵AD是中线,BC=20 m,∴BD=BC=10 m.
又∵102+242=262,即BD2+AD2=AB2,
∴△ABD是直角三角形.∴AD⊥BC.
∴S△ABC=BC·AD=×20×24=240(m2).
∵每平方米种植花草需要50元,
∴共需50×240=12 000(元).
答:种植这块三角形空地需要12 000元.
11.如图,在公路的同侧有A,B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8 km,BC=15 km,AB=17 km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5 km/h,问多长时间后这人距离B送奶站最近.
解:过点B作BD⊥CD于点D.
∵AC2+BC2=82+152=172=AB2.∴△ABC是直角三角形,
且∠ACB=90°.∵∠1=30°,∴∠BCD=60°.
在Rt△BCD中,∠BCD=60°,∴∠CBD=30°.
∴CD=BC=×15=7.5(km).
∵7.5÷2.5=3(h),
∴3 h后这人距离B送奶站最近.
12.某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2 ,休息区是一个三角形,边AE=8 m,求休息区的面积.
解:休息区的面积为24 m2.
13.如图是一个零件的示意图,量得AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
解:在△ABC中,∵AB=4,BC=3,∠ABC=90°,
∴根据勾股定理,得AC2=AB2+BC2=42+32=52.
∴AC=5.
∵AC2+CD2=52+122=25+144=169,
AD2=132=169,
∴AC2+CD2=AD2.
∴△ACD是直角三角形,且AD为斜边,
即∠ACD=90°.
14.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=.
(1)求AC,CE的长;
(2)求证:∠ACE=90°.
解:(1)∵在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC==
=.
∵在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE====2.
(2)证明:∵AC=,CE=,AE=,
∴AE2=AC2+CE2.∴∠ACE=90°.
15.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.
(1)求∠BAD的度数;
(2)求四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
解:(1)∠BAD=135°.
(2)S四边形ABCD=.
(3)S四边形ACB′D=.
16.阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
解:当n=1时,a=(m2-1),b=m,c=(m2+1),∵直角三角形有一边长为5,∴当a=5时,(m2-1)=5,m=±(舍去);当b=5时,m=5,则a=12,c=13;当c=5时,(m2+1)=5,m=±3,∵m>0,∴m=3,则a=4,b=3.综上所述,直角三角形的另外两条边长分别为12、13或3、4.
17.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边的平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? 是 (填“是”或“不是”);
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据;
(3)在Rt△ABC中,三边长分别为a,b,c,且a2=50,c2=100,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a.若Rt△ABC是奇异三角形,求a2∶b2∶c2.
解:(1)是
(2)∵12+()2=2×22,
∴该三角形是奇异三角形.
(3)当c为斜边时,b2=c2-a2=50,Rt△ABC不是奇异三角形;
当b为斜边时,b2=c2+a2=150,
∵50+150=2×100,∴a2+b2=2c2.
∴Rt△ABC是奇异三角形.
探究:在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
∵c>b>a,∴2c2>b2+a2,2a2∵Rt△ABC是奇异三角形,∴2b2=a2+c2.
∴2b2=a2+a2+b2.∴b2=2a2.∴c2=3a2.
∴a2∶b2∶c2=1∶2∶3.
第2课时 勾股定理及其逆定理的综合应用
一、选择题
1.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( )
A.正东或正西 B.正南 C.正北 D.正南或正北
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列选项中正确的是( )
A B C D
3.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
第3题图 第5题图 第6题图
4.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点.则线段BP长的最小值是( )
A. B.5 C. D.12
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( )
A.30° B.42° C.45° D.50°
二、填空题
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
8.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
三、解答题
10.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,
那么种植这块三角形空地需要多少钱?
11.如图,在公路的同侧有A,B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8 km,BC=15 km,AB=17 km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5 km/h,问多长时间后这人距离B送奶站最近.
12.某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2 ,休息区是一个三角形,边AE=8 m,求休息区的面积.
13.如图是一个零件的示意图,量得AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
14.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=.
(1)求AC,CE的长;
(2)求证:∠ACE=90°.
15.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.
(1)求∠BAD的度数;
(2)求四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
16.阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
17.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边的平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? (填“是”或“不是”);
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据;
(3)在Rt△ABC中,三边长分别为a,b,c,且a2=50,c2=100,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a.若Rt△ABC是奇异三角形,求a2∶b2∶c2.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.一辆汽车从点A出发沿正东方向行驶30 km到达点B,然后转向行驶40 km到达点C,最后从点C沿CA方向直接回到出发点A.如果汽车从出发到返回共行驶了120 km,那么BC的方向是( D )
A.正东或正西 B.正南 C.正北 D.正南或正北
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,下列选项中正确的是( C )
A B C D
3.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC的形状为( A )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对
第3题图 第5题图 第6题图
4.已知△ABC,AB=5,BC=12,AC=13,点P是AC上一个动点.则线段BP长的最小值是( A )
A. B.5 C. D.12
5.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( C )
A.250 km B.240 km C.200 km D.180 km
6.如图,在6×4的小正方形网格中,小正方形的边长均为1,点A,B,C,D,E均在格点上.则∠ABC-∠DCE=(提示:连接AC,AD)( C )
A.30° B.42° C.45° D.50°
【解析】连接AC,AD,如图,根据勾股定理可得AD=AC=BC=,CD=,∴∠ABC=∠BAC,在△ACD中,AD2+AC2=()2+()2=10,CD2=()2=10,∴AD2+AC2=CD2,∴△ACD是直角三角形,∠DAC=90°,∵AD=CD,∴△ACD是等腰直角三角形,∴∠ACD=45°,∵AB∥EC,∴∠BAC=∠ACE,∴∠ABC-∠DCE=∠BAC-∠DCE=∠ACE-∠DCE=∠ACD=45°.
二、填空题
7.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
【答案】13,84,85
8.某校要对如图所示的一块地进行绿化,已知AD=4 m,CD=3 m,AD⊥DC,AB=13 m,BC=12 m,则这块地的面积为 m2.
【答案】24
9.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
【答案】
三、解答题
10.某花园小区有一空地(如图所示的△ABC),为美化小区,居委会准备将其开发种植花草,经测量,AB=26 m,BC=20 m,BC边上的中线AD=24 m.如果每平方米种植花草需要50元,
那么种植这块三角形空地需要多少钱?
解:∵AD是中线,BC=20 m,∴BD=BC=10 m.
又∵102+242=262,即BD2+AD2=AB2,
∴△ABD是直角三角形.∴AD⊥BC.
∴S△ABC=BC·AD=×20×24=240(m2).
∵每平方米种植花草需要50元,
∴共需50×240=12 000(元).
答:种植这块三角形空地需要12 000元.
11.如图,在公路的同侧有A,B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8 km,BC=15 km,AB=17 km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5 km/h,问多长时间后这人距离B送奶站最近.
解:过点B作BD⊥CD于点D.
∵AC2+BC2=82+152=172=AB2.∴△ABC是直角三角形,
且∠ACB=90°.∵∠1=30°,∴∠BCD=60°.
在Rt△BCD中,∠BCD=60°,∴∠CBD=30°.
∴CD=BC=×15=7.5(km).
∵7.5÷2.5=3(h),
∴3 h后这人距离B送奶站最近.
12.某小区的一所健身中心的平面图如图所示,活动区是面积为200 m2的长方形,其长为20 m,餐饮区是一个半圆形,面积为4.5π m2 ,休息区是一个三角形,边AE=8 m,求休息区的面积.
解:休息区的面积为24 m2.
13.如图是一个零件的示意图,量得AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
解:在△ABC中,∵AB=4,BC=3,∠ABC=90°,
∴根据勾股定理,得AC2=AB2+BC2=42+32=52.
∴AC=5.
∵AC2+CD2=52+122=25+144=169,
AD2=132=169,
∴AC2+CD2=AD2.
∴△ACD是直角三角形,且AD为斜边,
即∠ACD=90°.
14.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=.
(1)求AC,CE的长;
(2)求证:∠ACE=90°.
解:(1)∵在Rt△ABC中,∠B=90°,AB=3,BC=2,
∴AC==
=.
∵在Rt△EDC中,∠D=90°,CD=6,DE=4,
∴CE====2.
(2)证明:∵AC=,CE=,AE=,
∴AE2=AC2+CE2.∴∠ACE=90°.
15.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.
(1)求∠BAD的度数;
(2)求四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
解:(1)∠BAD=135°.
(2)S四边形ABCD=.
(3)S四边形ACB′D=.
16.阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
解:当n=1时,a=(m2-1),b=m,c=(m2+1),∵直角三角形有一边长为5,∴当a=5时,(m2-1)=5,m=±(舍去);当b=5时,m=5,则a=12,c=13;当c=5时,(m2+1)=5,m=±3,∵m>0,∴m=3,则a=4,b=3.综上所述,直角三角形的另外两条边长分别为12、13或3、4.
17.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边的平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? 是 (填“是”或“不是”);
(2)若某三角形的三边长分别为1,,2,则该三角形是不是奇异三角形?请做出判断并写出判断依据;
(3)在Rt△ABC中,三边长分别为a,b,c,且a2=50,c2=100,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a.若Rt△ABC是奇异三角形,求a2∶b2∶c2.
解:(1)是
(2)∵12+()2=2×22,
∴该三角形是奇异三角形.
(3)当c为斜边时,b2=c2-a2=50,Rt△ABC不是奇异三角形;
当b为斜边时,b2=c2+a2=150,
∵50+150=2×100,∴a2+b2=2c2.
∴Rt△ABC是奇异三角形.
探究:在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
∵c>b>a,∴2c2>b2+a2,2a2
∴2b2=a2+a2+b2.∴b2=2a2.∴c2=3a2.
∴a2∶b2∶c2=1∶2∶3.
