冀教版八年级数学上册第13章13.3全等三角形的判定同步练习题(含答案)
文档属性
| 名称 | 冀教版八年级数学上册第13章13.3全等三角形的判定同步练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-13 07:54:37 | ||
图片预览


文档简介
冀教版八年级数学上册第13章13.3全等三角形的判定同步练习题(含答案)
一.选择题(共10小题)
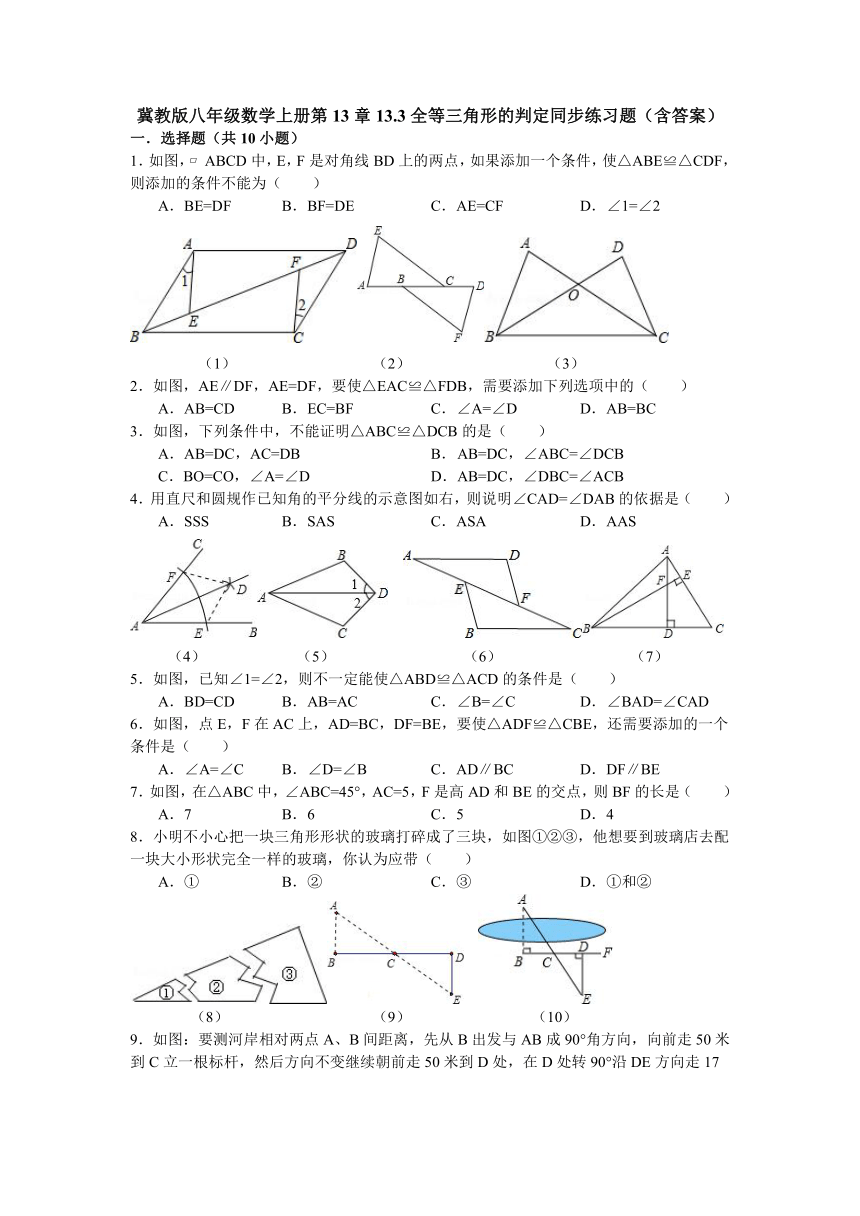
1.如图, ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
(1) (2) (3)
2.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD B. EC=BF C. ∠A=∠D D. AB=BC
3.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB B. AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D D. AB=DC,∠DBC=∠ACB
4.用直尺和圆规作已知角的平分线的示意图如右,则说明∠CAD=∠DAB的依据是( )
A.SSS B. SAS C. ASA D. AAS
(4) (5) (6) (7)
5.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
6.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE
7.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
A.7 B. 6 C. 5 D. 4
8.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.① B. ② C. ③ D. ①和②
(8) (9) (10)
9.如图:要测河岸相对两点A、B间距离,先从B出发与AB成90°角方向,向前走50米到C立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向走17米,到达E处,使A、C与E在同一直线上,那么测得A、B的距离为17米.这一作法的理论依据是( )
A.SSS B. SAS C. ASA D. AAS
10.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS B. SAS C. ASA D. AAS
二.填空题(共10小题)
11.如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件 ,使△ABD≌△CDB.(只需写一个)
(11) (12) (13) (14)
12.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
13.如图,在 ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形: .
14.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 (只填一个).
15.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为 .
(15) (16) (17)
16.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
17.如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.
18.(2015 武汉校级模拟)如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为 .
(18) (19) (20)
19.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
20.如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量内槽宽的卡钳,卡钳的工作原理利用了三角形全等判定定理 .
三.解答题(共5小题)
21.如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
22.如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDA,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
23.如图,已知AE=DB,BC=EF,BC∥EF,求证:△ABC≌△DEF.
24.如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
25.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
冀教版八年级数学上册第13章13.3全等三角形的判定同步练习题参考答案
一.选择题(共10小题)
1.C 2.A 3.D 4.A 5.B 6.B 7.C 8.C 9.C 10.C
二.填空题(共10小题)
11.AB=CD 12.∠ABD=∠CBD或AD=CD. 13.△ADF≌△BEC
14.AC=BD(或∠CBA=∠DAB) 15.30° 16.3 17.60 18.150° 19.90 20.SAS
三.解答题(共5小题)
21.解:∵AB∥DC,∴∠C=∠A,
∵AE=CF,∴AE+EF=CF+EF,
在△ABF和△CDE中,,∴△ABF≌△CDE(SAS).
22.解:选①AB=CD.理由如下:
∵∠BAC=∠CDB=90°,∴△BAC和△CDA是直角三角形,
在Rt△△BAC和Rt△CDA中,,∴Rt△BAC≌Rt△CDA(HL).
23.证明:∵BC∥EF,∴∠ABC=∠FED,
∵AE=BD,∴AE+BE=BD+BE,∴AB=DE,
在△ABC和△DEF中∴△ABC≌△DEF.
24.证明:∵∠1=∠2,∴∠CAB=∠DAE,
在△BAC和△DAE中,,∴△BAC≌△DAE(SAS),∴BC=DE.
25.证明:∵BF=EC(已知),∴BF+FC=EC+CF,即BC=EF,
在△ABC和△DEF中,,∴△ABC≌△DEF(AAS),
∴AC=DF(全等三角形对应边相等).
一.选择题(共10小题)
1.如图, ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
(1) (2) (3)
2.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
A.AB=CD B. EC=BF C. ∠A=∠D D. AB=BC
3.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB B. AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠D D. AB=DC,∠DBC=∠ACB
4.用直尺和圆规作已知角的平分线的示意图如右,则说明∠CAD=∠DAB的依据是( )
A.SSS B. SAS C. ASA D. AAS
(4) (5) (6) (7)
5.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
6.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE
7.如图,在△ABC中,∠ABC=45°,AC=5,F是高AD和BE的交点,则BF的长是( )
A.7 B. 6 C. 5 D. 4
8.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.① B. ② C. ③ D. ①和②
(8) (9) (10)
9.如图:要测河岸相对两点A、B间距离,先从B出发与AB成90°角方向,向前走50米到C立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向走17米,到达E处,使A、C与E在同一直线上,那么测得A、B的距离为17米.这一作法的理论依据是( )
A.SSS B. SAS C. ASA D. AAS
10.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS B. SAS C. ASA D. AAS
二.填空题(共10小题)
11.如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件 ,使△ABD≌△CDB.(只需写一个)
(11) (12) (13) (14)
12.如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
13.如图,在 ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形: .
14.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 (只填一个).
15.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为 .
(15) (16) (17)
16.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
17.如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.
18.(2015 武汉校级模拟)如图,在等腰△ABC中,AB=CB,M为△ABC内一点,∠MAC+∠MCB=∠MCA=30°,则∠BMC的度数为 .
(18) (19) (20)
19.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE= 度.
20.如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量内槽宽的卡钳,卡钳的工作原理利用了三角形全等判定定理 .
三.解答题(共5小题)
21.如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
22.如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDA,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
23.如图,已知AE=DB,BC=EF,BC∥EF,求证:△ABC≌△DEF.
24.如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
25.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
冀教版八年级数学上册第13章13.3全等三角形的判定同步练习题参考答案
一.选择题(共10小题)
1.C 2.A 3.D 4.A 5.B 6.B 7.C 8.C 9.C 10.C
二.填空题(共10小题)
11.AB=CD 12.∠ABD=∠CBD或AD=CD. 13.△ADF≌△BEC
14.AC=BD(或∠CBA=∠DAB) 15.30° 16.3 17.60 18.150° 19.90 20.SAS
三.解答题(共5小题)
21.解:∵AB∥DC,∴∠C=∠A,
∵AE=CF,∴AE+EF=CF+EF,
在△ABF和△CDE中,,∴△ABF≌△CDE(SAS).
22.解:选①AB=CD.理由如下:
∵∠BAC=∠CDB=90°,∴△BAC和△CDA是直角三角形,
在Rt△△BAC和Rt△CDA中,,∴Rt△BAC≌Rt△CDA(HL).
23.证明:∵BC∥EF,∴∠ABC=∠FED,
∵AE=BD,∴AE+BE=BD+BE,∴AB=DE,
在△ABC和△DEF中∴△ABC≌△DEF.
24.证明:∵∠1=∠2,∴∠CAB=∠DAE,
在△BAC和△DAE中,,∴△BAC≌△DAE(SAS),∴BC=DE.
25.证明:∵BF=EC(已知),∴BF+FC=EC+CF,即BC=EF,
在△ABC和△DEF中,,∴△ABC≌△DEF(AAS),
∴AC=DF(全等三角形对应边相等).
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
