2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:2.2 轴对称的基本性质
文档属性
| 名称 | 2015-2016山东省泰安市岱岳区八上数学(青岛版)学案:2.2 轴对称的基本性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-15 00:00:00 | ||
图片预览


文档简介
课题 2.2 轴对称的基本性质(第1课时) 课型 新授
内容 八上教科书34---36页 主备人 王存如
学习目标 1、经历探索轴对称图形的性质的过程;2、理解轴对称中对应点、对应线段、对应角的性质;3、会画出与已知图形关于某直线对称的图形
重点 准确理解成轴对称的两个图形的基本性质。
难点 应用轴对称的性质解决一些实际问题。
学前预习案
独立阅读34---36页的内容,约8分钟,要求:问题:成轴对称的两个图形具有哪些性质呢?它们的大小和位置有什么关系?操作:在纸上任意画一点A,把纸对折,用针在点A处穿孔,再把纸展开,并连接两针孔A、A’。探索:线段AA’与折痕l之间有什么关系?问题1:如果把纸重新折叠,因为A、A’重合,那么线段OA、O A’_______ ;此时O是线段A A’的____________ 。 问题2:∠1与∠2有什么关系? 问题3:折痕l与A A’什么关系?
课堂学习案
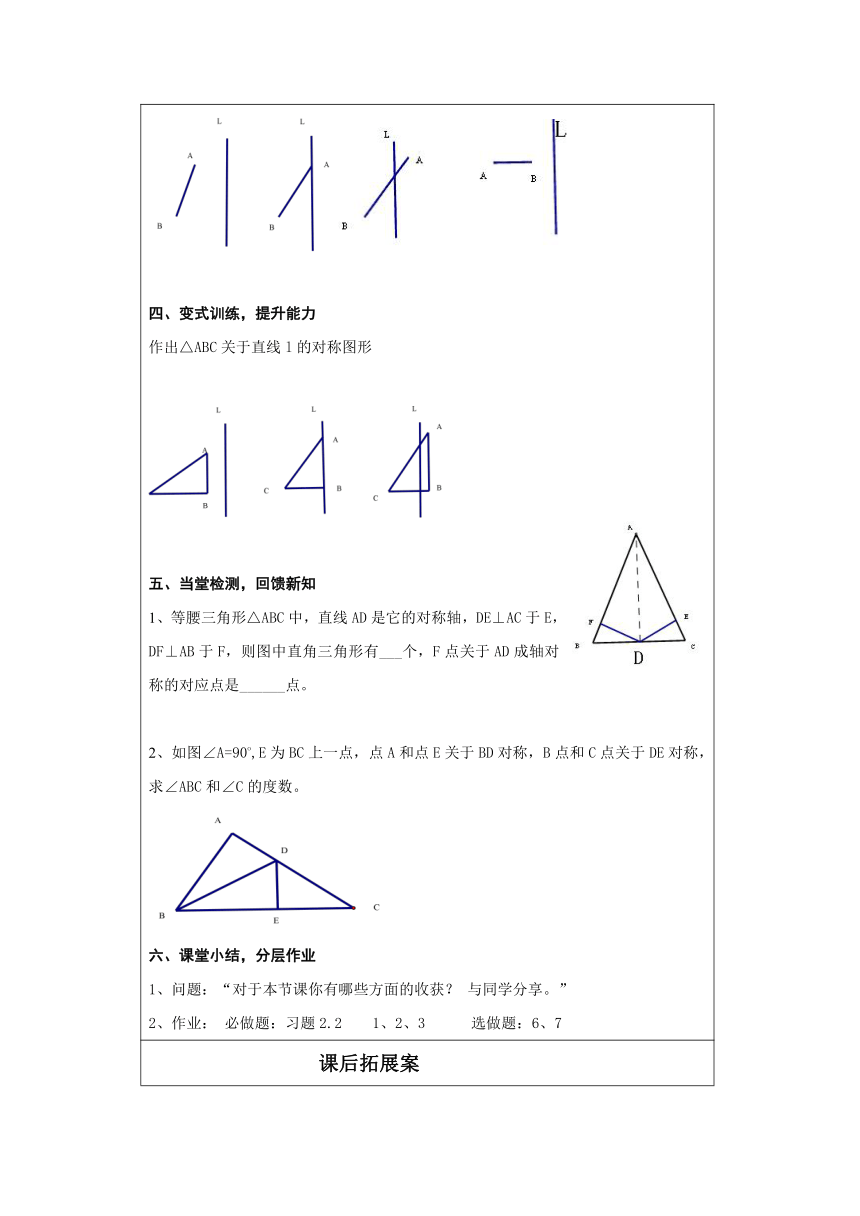
一、创设情境,导入新课操作:取一张长方形的纸片,按下面步骤做一做。将长方形纸片对折,折痕为l,(1)在纸上画△ABC;(2)用针尖沿△ABC各边扎几个小孔(3)将纸展开,连接AA’、BB’、CC’线段AA’、BB’、CC’与折痕l有什么关系?二、自主探究,归纳新知问题1:上图中,线段与有什么关系?与呢?线段与有什么关系?与呢?说说你的理由。问题2:图中,与有什么关系?与呢?与有什么关系?为什么?问题3:轴对称有哪些性质?归纳:轴对称的 ( http: / / www.21cnjy.com )性质: ________________ 。三、应用练习,巩固新知1、如图,△ABC与△A’B’C’关于直线l对称,则∠B的度数为( )A、30o B、50o C、90o D、100o2、如图,∠MON内一点P,P点关于OM的 ( http: / / www.21cnjy.com )对称点是G,P点关于ON的对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,则△PAB的周长为( )A、5cm B、10cm C、20cm D、15cm3、如图是一个风筝的图案,它是轴对称图形, ( http: / / www.21cnjy.com )量得∠B的度数=30o,则∠E的大小为( ) A、30o B、35o C、40o D、45o4、作出线段AB关于直线l的对称图形 ( http: / / www.21cnjy.com )四、变式训练,提升能力作出△ABC关于直线l的对称图形五、当堂检测,回馈新知1、等腰三角形△ABC中, ( http: / / www.21cnjy.com )直线AD是它的对称轴,DE⊥AC于E,DF⊥AB于F,则图中直角三角形有___个,F点关于AD成轴对称的对应点是______点。2、如图∠A=90o,E为BC上一点,点A和点E关于BD对称,B点和C点关于DE对称,求∠ABC和∠C的度数。 ( http: / / www.21cnjy.com )六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.2 1、2、3 选做题:6、7
课后拓展案
1、下列图形中,线段AB和A’B’( AB=A’ B’)不关于直线l对称的是( ) ( http: / / www.21cnjy.com )A B C D2、如图,AB=AC=4cm,BC=3 ( http: / / www.21cnjy.com )cm,∠A=40o,点A和点B关于直线l对称,AC与l相交于点D,则∠C=____,△BDC的周长是_______。 ( http: / / www.21cnjy.com )
课题 2.2 轴对称的基本性质(第2课时) 课型 新授
内容 八上教科书37---38页 主备人 王存如
学习目标 1、知道x轴、y轴对称的点的坐标的特点;2、能作关于坐标轴(x轴、y轴)对称的三角形。
重点 知道关于x轴、y轴对称的点的坐标规律
难点 能作出关于x轴、y轴对称的几何图形
学前预习案
独立阅读37---38页的内容,约5分钟,要 ( http: / / www.21cnjy.com )求:1、把一个图形沿某条直线折叠后,得 ( http: / / www.21cnjy.com )到一个与它全等的图形,图形的这种变化叫做___________________。这条直线叫做______________________。 2、用笔尖扎重叠的纸可以得到成轴对称的两个图案。(1)找出它的两对对应点、对称轴(2)用测量的方法验证你找到的对应点所连线段分别被对称轴垂直平分。 3、成轴对称的两个图形中,对应点的 ( http: / / www.21cnjy.com )连线被对称轴 ________________________。 4、在直角坐标系中,点(a,b)关于y轴的对称点是 _______________ ,关于x轴的对称点是_________________。
课堂学习案
一、创设情境,导入新课1、投影展示蝴蝶、风筝和飞机的图片,激趣引入。2、提问:什么是轴对称?什么是轴对称图形?轴对称与轴对称图形有什么区别?3、提问轴对称的性质是什么? 二、自主探究,归纳新知1、学习课本37页中的“观察与思考”,将自己的操作与小组中的操作交流一下,看谁的制作更精准。2、归纳:在直角坐标系中, ( http: / / www.21cnjy.com )点(a,b)关于y轴的对称点是 ,关于x轴的对称点是 。三、应用练习,巩固新知1、在直角坐标系中,分别写出下列各点关于x轴与y轴的对称点的坐标:A(2,1) B(-5,4) C(0,1) D(-2,0) O(0,0) F(m,n)2、边长为2的正方形放在 ( http: / / www.21cnjy.com )如图所示的直角坐标系中,各顶点关于x轴的对称点的坐标是______________;各顶点关于y轴的对称点的坐标是________________;3、课本中练习1、2四、变式训练,提升能力例:在直角坐标系中,△ABC的三个顶点 ( http: / / www.21cnjy.com )为A(-2,1)、B(1.5,-4)、C(0,3)。试写出△ABC关于x轴和y轴成轴对称的三角形的三个顶点的坐标,并在直角坐标系中画出来。五、当堂检测,回馈新知1、在平面直角坐标系中,点P(-1,2)关于x轴的对称点的坐标为( ) A、(-1,-2) B、(1,-2) C、(2,-1) D、(-2,1)2、若点A(2,a)关于x轴的对称点是B(b,-3),则ab的值是 3、如图,△ABC在平面直角坐标系中第 ( http: / / www.21cnjy.com )二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是( )A(-3,2)B(2,-3)C(1,-2)D(3,-1)六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.2 4、5 选做题:8
课后拓展案
1.已知点A(2,-3)与点B关于x轴对称,则点B在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限2、(1)已知点P(a+b ,7),Q(6,3a-2b)关于x轴对称,试求a ,b的值。 (2)设点M(2a-3,3-a)关于y轴的对称点在第二象限,且a为整数,试求点M的坐标。
内容 八上教科书34---36页 主备人 王存如
学习目标 1、经历探索轴对称图形的性质的过程;2、理解轴对称中对应点、对应线段、对应角的性质;3、会画出与已知图形关于某直线对称的图形
重点 准确理解成轴对称的两个图形的基本性质。
难点 应用轴对称的性质解决一些实际问题。
学前预习案
独立阅读34---36页的内容,约8分钟,要求:问题:成轴对称的两个图形具有哪些性质呢?它们的大小和位置有什么关系?操作:在纸上任意画一点A,把纸对折,用针在点A处穿孔,再把纸展开,并连接两针孔A、A’。探索:线段AA’与折痕l之间有什么关系?问题1:如果把纸重新折叠,因为A、A’重合,那么线段OA、O A’_______ ;此时O是线段A A’的____________ 。 问题2:∠1与∠2有什么关系? 问题3:折痕l与A A’什么关系?
课堂学习案
一、创设情境,导入新课操作:取一张长方形的纸片,按下面步骤做一做。将长方形纸片对折,折痕为l,(1)在纸上画△ABC;(2)用针尖沿△ABC各边扎几个小孔(3)将纸展开,连接AA’、BB’、CC’线段AA’、BB’、CC’与折痕l有什么关系?二、自主探究,归纳新知问题1:上图中,线段与有什么关系?与呢?线段与有什么关系?与呢?说说你的理由。问题2:图中,与有什么关系?与呢?与有什么关系?为什么?问题3:轴对称有哪些性质?归纳:轴对称的 ( http: / / www.21cnjy.com )性质: ________________ 。三、应用练习,巩固新知1、如图,△ABC与△A’B’C’关于直线l对称,则∠B的度数为( )A、30o B、50o C、90o D、100o2、如图,∠MON内一点P,P点关于OM的 ( http: / / www.21cnjy.com )对称点是G,P点关于ON的对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,则△PAB的周长为( )A、5cm B、10cm C、20cm D、15cm3、如图是一个风筝的图案,它是轴对称图形, ( http: / / www.21cnjy.com )量得∠B的度数=30o,则∠E的大小为( ) A、30o B、35o C、40o D、45o4、作出线段AB关于直线l的对称图形 ( http: / / www.21cnjy.com )四、变式训练,提升能力作出△ABC关于直线l的对称图形五、当堂检测,回馈新知1、等腰三角形△ABC中, ( http: / / www.21cnjy.com )直线AD是它的对称轴,DE⊥AC于E,DF⊥AB于F,则图中直角三角形有___个,F点关于AD成轴对称的对应点是______点。2、如图∠A=90o,E为BC上一点,点A和点E关于BD对称,B点和C点关于DE对称,求∠ABC和∠C的度数。 ( http: / / www.21cnjy.com )六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.2 1、2、3 选做题:6、7
课后拓展案
1、下列图形中,线段AB和A’B’( AB=A’ B’)不关于直线l对称的是( ) ( http: / / www.21cnjy.com )A B C D2、如图,AB=AC=4cm,BC=3 ( http: / / www.21cnjy.com )cm,∠A=40o,点A和点B关于直线l对称,AC与l相交于点D,则∠C=____,△BDC的周长是_______。 ( http: / / www.21cnjy.com )
课题 2.2 轴对称的基本性质(第2课时) 课型 新授
内容 八上教科书37---38页 主备人 王存如
学习目标 1、知道x轴、y轴对称的点的坐标的特点;2、能作关于坐标轴(x轴、y轴)对称的三角形。
重点 知道关于x轴、y轴对称的点的坐标规律
难点 能作出关于x轴、y轴对称的几何图形
学前预习案
独立阅读37---38页的内容,约5分钟,要 ( http: / / www.21cnjy.com )求:1、把一个图形沿某条直线折叠后,得 ( http: / / www.21cnjy.com )到一个与它全等的图形,图形的这种变化叫做___________________。这条直线叫做______________________。 2、用笔尖扎重叠的纸可以得到成轴对称的两个图案。(1)找出它的两对对应点、对称轴(2)用测量的方法验证你找到的对应点所连线段分别被对称轴垂直平分。 3、成轴对称的两个图形中,对应点的 ( http: / / www.21cnjy.com )连线被对称轴 ________________________。 4、在直角坐标系中,点(a,b)关于y轴的对称点是 _______________ ,关于x轴的对称点是_________________。
课堂学习案
一、创设情境,导入新课1、投影展示蝴蝶、风筝和飞机的图片,激趣引入。2、提问:什么是轴对称?什么是轴对称图形?轴对称与轴对称图形有什么区别?3、提问轴对称的性质是什么? 二、自主探究,归纳新知1、学习课本37页中的“观察与思考”,将自己的操作与小组中的操作交流一下,看谁的制作更精准。2、归纳:在直角坐标系中, ( http: / / www.21cnjy.com )点(a,b)关于y轴的对称点是 ,关于x轴的对称点是 。三、应用练习,巩固新知1、在直角坐标系中,分别写出下列各点关于x轴与y轴的对称点的坐标:A(2,1) B(-5,4) C(0,1) D(-2,0) O(0,0) F(m,n)2、边长为2的正方形放在 ( http: / / www.21cnjy.com )如图所示的直角坐标系中,各顶点关于x轴的对称点的坐标是______________;各顶点关于y轴的对称点的坐标是________________;3、课本中练习1、2四、变式训练,提升能力例:在直角坐标系中,△ABC的三个顶点 ( http: / / www.21cnjy.com )为A(-2,1)、B(1.5,-4)、C(0,3)。试写出△ABC关于x轴和y轴成轴对称的三角形的三个顶点的坐标,并在直角坐标系中画出来。五、当堂检测,回馈新知1、在平面直角坐标系中,点P(-1,2)关于x轴的对称点的坐标为( ) A、(-1,-2) B、(1,-2) C、(2,-1) D、(-2,1)2、若点A(2,a)关于x轴的对称点是B(b,-3),则ab的值是 3、如图,△ABC在平面直角坐标系中第 ( http: / / www.21cnjy.com )二象限内,顶点A的坐标是(﹣2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是( )A(-3,2)B(2,-3)C(1,-2)D(3,-1)六、课堂小结,分层作业1、问题:“对于本节课你有哪些方面的收获? 与同学分享。”2、作业: 必做题:习题2.2 4、5 选做题:8
课后拓展案
1.已知点A(2,-3)与点B关于x轴对称,则点B在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限2、(1)已知点P(a+b ,7),Q(6,3a-2b)关于x轴对称,试求a ,b的值。 (2)设点M(2a-3,3-a)关于y轴的对称点在第二象限,且a为整数,试求点M的坐标。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
