第九章 图形的相似 专题1 平行线分线段成比例常见应用的六种技巧(含答案)
文档属性
| 名称 | 第九章 图形的相似 专题1 平行线分线段成比例常见应用的六种技巧(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 09:08:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
专题1 平行线分线段成比例常见应用的六种技巧
技巧1 等线段代换法证比例式
1.如图,在 中,D,E 分别是 BC,AC 上的点,连接DE 并延长与BA 的延长线交于点 F,且 求证:
技巧2 等积代换法证比例式
2. 如图,在 中,D 是 AB 上一点,E 是内一点, 过点 D 作 AC 的平行线交 CE 的延长线于点 F,CF 与AB交于点P,求证:
3.如图,已知点A,C,E和点B,F,D分别是 两边上的点,且 ∥∥
求证:
技巧3 等比代换法证比例式
4.如图,在 中, 点D 在BC 边上,连接AD,点E 在AC边上,过点 E 作 EF∥BC,交 AD 于点F,过点 E 作EG∥AB,交BC 于点 G,则下列式子一定正确的是( )
5.如图,已知 ∥∥求AD的长.
技巧4 平行法证比例式
6.如图,已知B,C,E三点在同一条直线上, 与 都是等边三角形,其中线段 BD 交 AC于点 G,线段AE 交 CD 于点 F,连接 GF.求证:
技巧5 等比例过渡法证线段相等
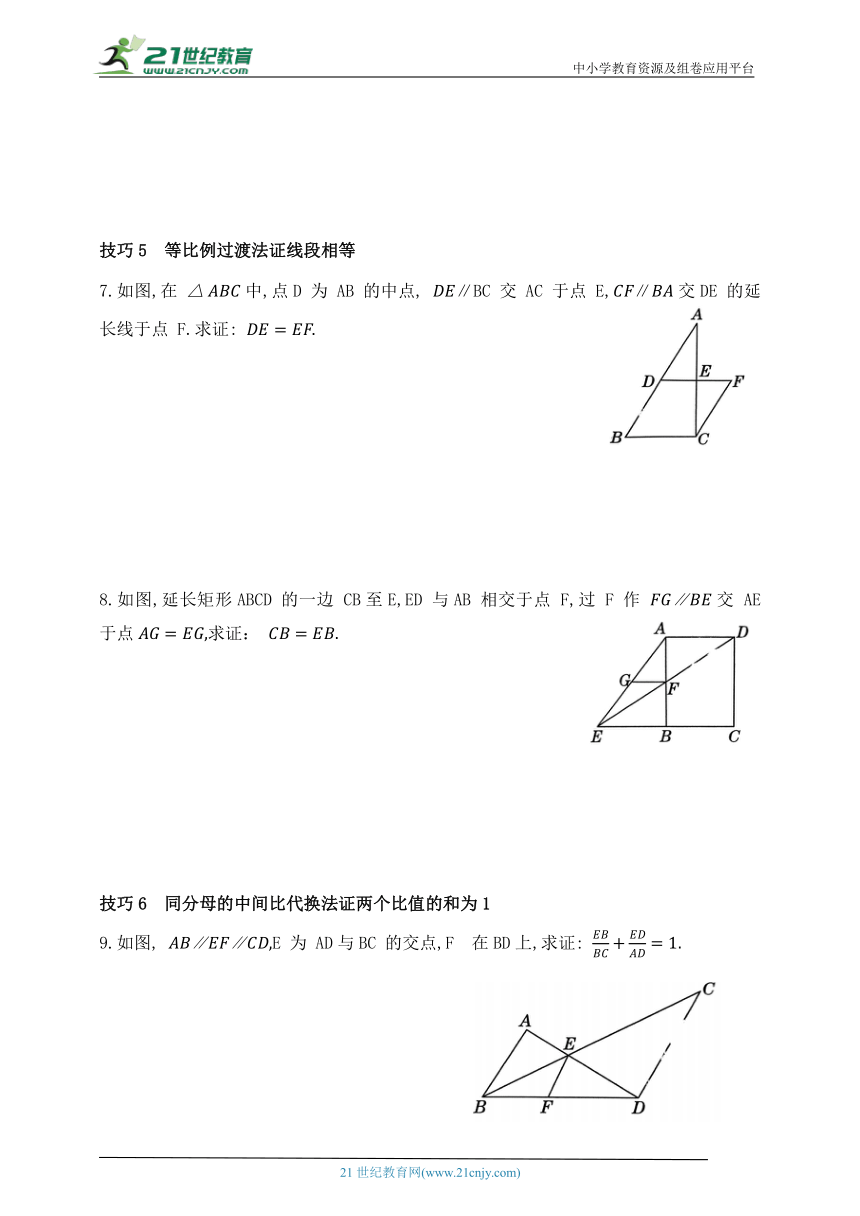
7.如图,在 中,点D 为 AB 的中点, ∥BC 交 AC 于点 E,∥交DE 的延长线于点 F.求证:
8.如图,延长矩形ABCD 的一边 CB至E,ED 与AB 相交于点 F,过 F 作 ∥交 AE 于点求证:
技巧6 同分母的中间比代换法证两个比值的和为1
9.如图, ∥∥E 为 AD与BC 的交点,F 在BD上,求证:
参考答案
1.【证明】如图,过点 A 作 ∥交 BD 于 M,则
2.【证明】·
∥
3.【证明】 ∥即 ,
即 即
4. C 【点拨】∵ ∥
∥
5.【解】 ∥∥
6.【证明】(1)∵△ABC与△DCE都是等边三角形,
∴AC=BC,CE=CD,∠DCE=∠ACB=60°,∴∠DCE+∠ACD=∠ACB+∠ACD,即∠ACE=∠BCD.
∴△ACE≌△BCD.
(2)∵△ACE≌△BCD,∴∠BDC =∠AEC.
又∵ ∠GCD = 180°- ∠ACB - ∠DCE = 60°=∠FCE,CD=CE,∴△GCD≌△FCE(ASA).
∴CG=CF.∴△CFG为等边三角形.∴∠CFG=60°.∴∠CFG=∠DCE.∴GF∥CE.
7.【证明】 ∥
∵ 点D 为AB的中点,∴AD=DB,即
∥
8. 【证明】∵ 四边形ABCD 为矩形, ∥
又∵ AG=EG,∴
9.【证明】 ∥
∥
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
专题1 平行线分线段成比例常见应用的六种技巧
技巧1 等线段代换法证比例式
1.如图,在 中,D,E 分别是 BC,AC 上的点,连接DE 并延长与BA 的延长线交于点 F,且 求证:
技巧2 等积代换法证比例式
2. 如图,在 中,D 是 AB 上一点,E 是内一点, 过点 D 作 AC 的平行线交 CE 的延长线于点 F,CF 与AB交于点P,求证:
3.如图,已知点A,C,E和点B,F,D分别是 两边上的点,且 ∥∥
求证:
技巧3 等比代换法证比例式
4.如图,在 中, 点D 在BC 边上,连接AD,点E 在AC边上,过点 E 作 EF∥BC,交 AD 于点F,过点 E 作EG∥AB,交BC 于点 G,则下列式子一定正确的是( )
5.如图,已知 ∥∥求AD的长.
技巧4 平行法证比例式
6.如图,已知B,C,E三点在同一条直线上, 与 都是等边三角形,其中线段 BD 交 AC于点 G,线段AE 交 CD 于点 F,连接 GF.求证:
技巧5 等比例过渡法证线段相等
7.如图,在 中,点D 为 AB 的中点, ∥BC 交 AC 于点 E,∥交DE 的延长线于点 F.求证:
8.如图,延长矩形ABCD 的一边 CB至E,ED 与AB 相交于点 F,过 F 作 ∥交 AE 于点求证:
技巧6 同分母的中间比代换法证两个比值的和为1
9.如图, ∥∥E 为 AD与BC 的交点,F 在BD上,求证:
参考答案
1.【证明】如图,过点 A 作 ∥交 BD 于 M,则
2.【证明】·
∥
3.【证明】 ∥即 ,
即 即
4. C 【点拨】∵ ∥
∥
5.【解】 ∥∥
6.【证明】(1)∵△ABC与△DCE都是等边三角形,
∴AC=BC,CE=CD,∠DCE=∠ACB=60°,∴∠DCE+∠ACD=∠ACB+∠ACD,即∠ACE=∠BCD.
∴△ACE≌△BCD.
(2)∵△ACE≌△BCD,∴∠BDC =∠AEC.
又∵ ∠GCD = 180°- ∠ACB - ∠DCE = 60°=∠FCE,CD=CE,∴△GCD≌△FCE(ASA).
∴CG=CF.∴△CFG为等边三角形.∴∠CFG=60°.∴∠CFG=∠DCE.∴GF∥CE.
7.【证明】 ∥
∵ 点D 为AB的中点,∴AD=DB,即
∥
8. 【证明】∵ 四边形ABCD 为矩形, ∥
又∵ AG=EG,∴
9.【证明】 ∥
∥
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
