人教版八年级下册 18.1 平行四边形 经典同步练习题 含解析
文档属性
| 名称 | 人教版八年级下册 18.1 平行四边形 经典同步练习题 含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 00:00:00 | ||
图片预览



文档简介
人教版八年级下册 18.1 平行四边形 经典同步练习题
一.选择题
1.在平行四边形ABCD中,∠A+∠C=100°,则∠D等于( )
A.50° B.80° C.100° D.130°
2.如图,A,B两地被池塘隔开,小明先在AB外选一点C,然后测出AC,BC的中点M,N.若MN的长为18米,则A,B间的距离是( )
A.9米 B.18米 C.27米 D.36米
3.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.一组对边平行,一组对角相等的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.一组对边平行,一组邻边相等的四边形是平行四边形
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成了一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.③④ C.②③ D.①④
5.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
6.如图,已知平行四边形ABCD中A、C、D三点的坐标,则点B的坐标为( )
A.(﹣3,﹣2) B.(﹣2,﹣2) C.(﹣3,﹣1) D.(﹣2,﹣1)
7.如图所示, ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5, ABCD的周长( )
A.11 B.13 C.16 D.22
8.已知直线a,b,c在同一平面内,且a∥b∥c,a与b之间的距离为5cm,b与c之间的距离为3cm,则a与c之间的距离是( )
A.2cm B.8cm
C.2cm或8cm D.以上都不对
9.如图,平行四边形ABCD中,E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
10.如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒2.5cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q也停止运动.设运动时间为t s,开始运动以后,当t为何值时,以P,D,Q,B为顶点的四边形是平行四边形?( )
A. B. C.或 D.或
二.填空题
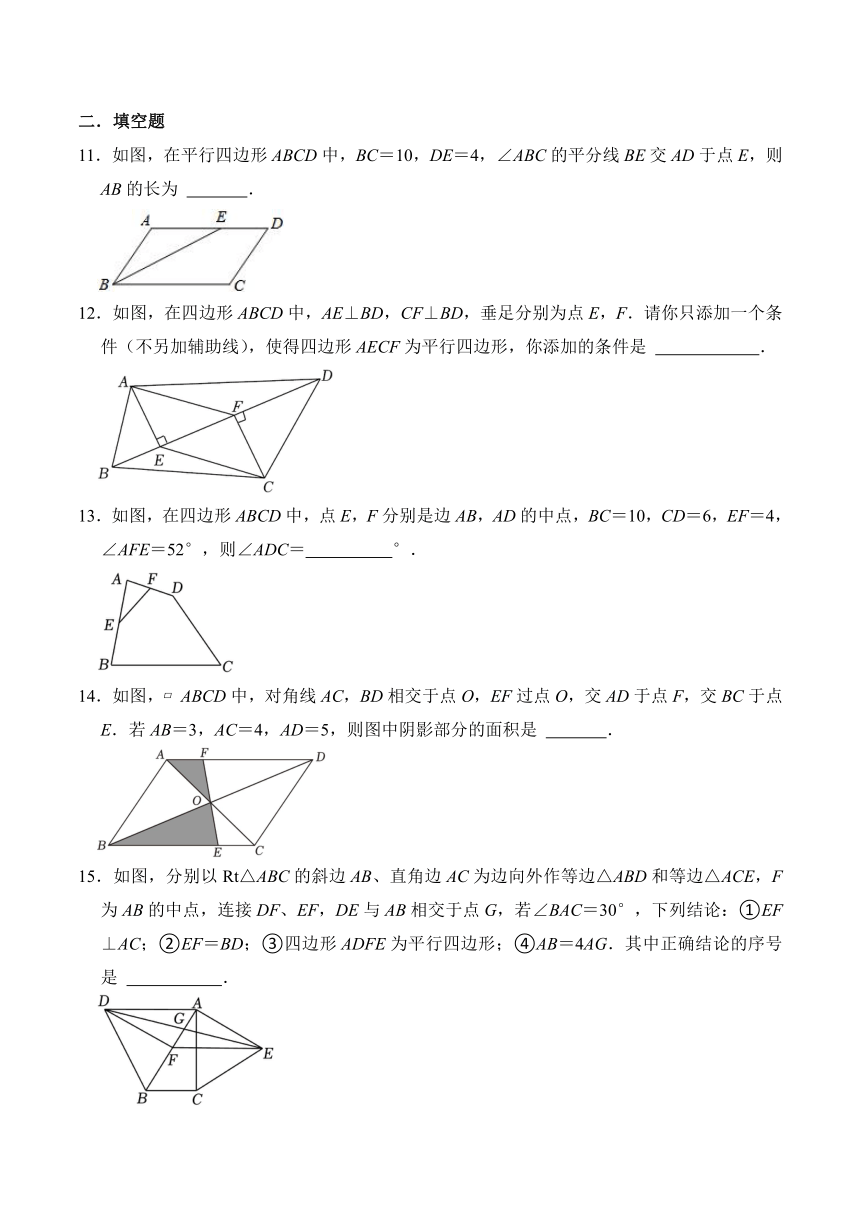
11.如图,在平行四边形ABCD中,BC=10,DE=4,∠ABC的平分线BE交AD于点E,则AB的长为 .
12.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是 .
13.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=10,CD=6,EF=4,∠AFE=52°,则∠ADC= °.
14.如图, ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是 .
15.如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,连接DF、EF,DE与AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②EF=BD;③四边形ADFE为平行四边形;④AB=4AG.其中正确结论的序号是 .
三.解答题
16.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
17.如图,四边形ABCD是平行四边形,AC=AD,AE⊥BC,DF⊥AC,垂足分别为E,F.证明AE=DF.
18.如图,已知在 ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,连接AC.求证:四边形ACHE是平行四边形.
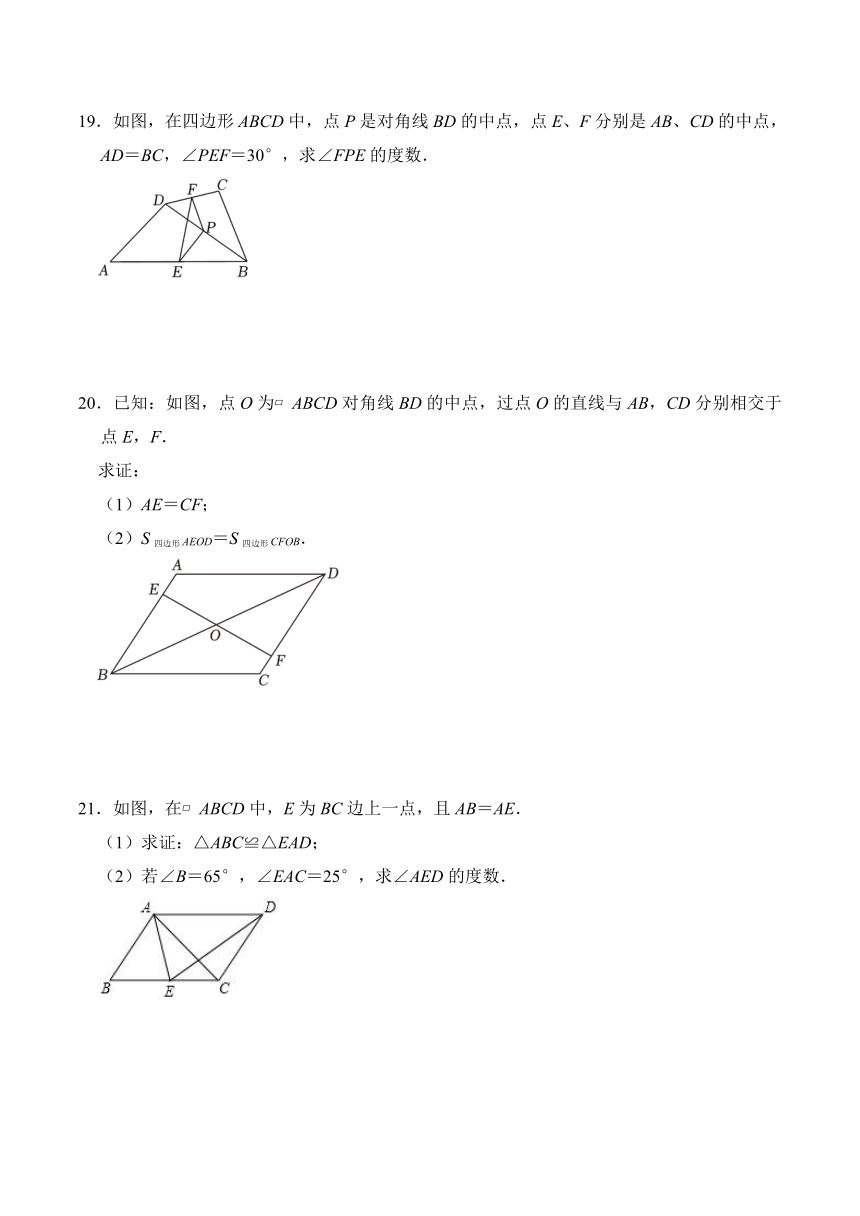
19.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,求∠FPE的度数.
20.已知:如图,点O为 ABCD对角线BD的中点,过点O的直线与AB,CD分别相交于点E,F.
求证:
(1)AE=CF;
(2)S四边形AEOD=S四边形CFOB.
21.如图,在 ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°.
(1)求证:AB=AE;
(2)若=m(0<m<1),AC=4,连接OE;
①若m=,求平行四边形ABCD的面积;
②设=k,试求k与m满足的关系.
参考答案
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠A+∠D=180°,
∵∠A+∠C=100°,
∴∠A=50°,
∴∠D=180°﹣∠A=130°.
故选:D.
2.解:∵点M,N分别是AC,BC的中点,
∴MN是△ABC的中位线,
∴AB=2MN,
∵MN=18米,
∴AB=36米,
故选:D.
3.解:A、一组对边平行,另一组对边相等的四边形不一定是平行四边形,也可以是等腰梯形,故本选项错误;
B、一组对边平行,一组对角相等的四边形可证出另一组对边也平行,所以该四边形是平行四边形,故本选项正确;
C、一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,故本选项错误;
D、一组对边平行,一组邻角互补的四边形有可能是梯形或平行四边形,故本选项错误;
故选:B.
4.解:∵只有③④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带③④两块碎玻璃,就可以确定平行四边形的大小.
故选:B.
5.解:设BC=x,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴BC+CD=20,
∴CD=20﹣x,
∵AE⊥BC于点E,AF⊥CD于点F,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20﹣x),
解得:x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:D.
6.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵A(﹣1,2),D(3,2),
∴AD=4=BC,
∵C(2,﹣1),
∴B(﹣2,﹣1),
故选:D.
7.解:∵ ABCD的对角线AC,BD相交于点O,
∴OA=OC,AD=BC,AB=CD=5,
∵AE=EB,OE=3,
∴BC=2OE=6,
∴ ABCD的周长=2×(AB+BC)=22.
故选:D.
8.解:如图①,a与c之间的距离为5+3=8(cm);
如图②,a与c之间的距离为5﹣3=2(cm).
∴a与c之间的距离为8cm或2cm.
故选:C.
9.解:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∵E,F分别AB,CD的中点
∴AE=EB=DF=FC
∴四边形AEFD是平行四边形,四边形EFCB是平行四边形,四边形AFCE是平行四边形,四边形EDFB是平行四边形,四边形GEHF是平行四边形.
∴平行四边形的个数共有6个.
故选:D.
10.解:∵四边形ABCD为平行四边形,
∴PD∥BQ.
若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.
设运动时间为t.
当0<t≤4时,AP=t,PD=10﹣t,CQ=2.5t,BQ=10﹣2.5t,
∴10﹣t=10﹣2.5t,
1.5t=0,
∴t=0(舍去);
当4<t≤8时,AP=t,PD=10﹣t,BQ=2.5t﹣10,
∴10﹣t=2.5t﹣10,
解得:t=;
当8<t≤10时,AP=t,PD=10﹣t,CQ=2.5t﹣20,BQ=30﹣2.5t,
∴10﹣t=30﹣2.5t,
解得:t=(舍去);
综上所述,t的值为时,以P,D,Q,B为顶点的四边形是平行四边形.
故选:B.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10.
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=BC﹣DE=10﹣4=6,
故答案为:6.
12.解:添加条件为:AE=CF,
理由:∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AE=CF,
∴四边形AECF为平行四边形,
故答案为:AE=CF.
13.解:连接BD,
∵点E、F分别是边AB、AD的中点,
∴BD=2EF=8,EF∥BD,
∴∠ADB=∠AFE=52°,
BD2+CD2=100,BC2=100,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=142°,
故答案为:142.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,
∴∠OBE=∠ODF,
∵∠BOE=∠DOF,
∴△BOE≌△DOF(AAS),
∴S阴影=S△AOD=S平行四边形ABCD,
∵AB=3,AC=4,BC=AD=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴S阴影=S△AOD=S平行四边形ABCD=3,
故答案为:3.
15.解:如图,
连接CF,
∵∠ACB=90°,点F是AB的中点,
∴CF=AF,
∵△ACE是等边三角形,
∴AE=CE,
∴EF⊥AC,
故①正确;
∵△ABD是等边三角形,△ACE是等边三角形,
∴AD=BD,DAB=60°,∠CAE=60°,
∴∠BAE=∠BAC+∠CAE=90°,
∵点F是AB的中点,
∴DF⊥AB,
∴∠DFA=∠BAE=90°,
∴DF∥AE,
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=∠ADC=60°,
∴AD∥BC,
由①知:AC⊥EF,BC⊥AC,
∴EF∥BC,
∴AD∥EF,
∴四边形ADFE是平行四边形,
故③正确;
∵四边形ADFE是平行四边形,
∴AD=EF,
∵AD=BD,
∴EF=BD,故②正确;
∵四边形ADFE是平行四边形,
∴AF=2AG,
∵AD=AB,AB=2AF,
∴AB=4AG,
故④正确;
故答案为:①②③④.
三.解答题
16.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE,
∵AD=6,EF=3,
∴AF+DE=AD﹣EF=3,
∴AF=.
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠ACE,
∵AE⊥BC,DF⊥AC,
∴∠AEC=∠AFD=90°,
在△ADF与△ACE中,
,
∴△ADF≌△ACE(AAS),
∴AE=DF.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CH.
∵点E、F分别是边AD、CD的中点,
∴EF∥AC,即EH∥AC,
∴四边形ACHE是平行四边形.
19.解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=BC,PE=AD,
∵AD=BC,
∴PF=PE,
∴△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°,
∴∠FPE=180°﹣∠PEF﹣∠PFE=180°﹣30°﹣30°=120°.
20.证明:(1)∵点O为对角线BD的中点,
∴OB=OD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠EBO=∠FDO,
在△EBO和△FDO中,
,
∴△EBO≌△FDO(ASA),
∴BE=DF,
∴AB﹣BE=CD﹣DF,
即AE=CF;
(2)∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD=S平行四边形ABCD,
由(1)得:△EBO≌△FDO,
∴S△EBO=S△FDO,
∴S△ABD﹣S△EBO=S△CBD﹣S△FDO,
即S四边形AEOD=S四边形CFOB.
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AB=AE;
(2)解:①∵=m=,
∴AB=BC,
∴AE=BE=BC,
∴AE=CE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠AEB=60°,
∴∠ACE=∠CAE=30°,
∴∠BAC=90°,
当AC=4时,AB=4,
∴平行四边ABCD的面积=2S△ABC=2×AB AC=4×4=16;
②∵四边形ABCD是平行四边形,
∴S△AOD=S△BOC,S△BOC=S△BCD,
∵△ABE是等边三角形,
∴BE=AB=mBC,
∵△BOE的BE边上的高等于△BDC的BC边上的高的一半,底BE等于BC的m倍,
设BC边上的高为h,BC的长为b,
∴S△BCD=×bh,S△OBE=××mb=,
∴S四边形OECD=S△BCD﹣S△OBE=﹣=(﹣)bh,
∵S△AOD=×b=,
∴=(﹣)bh×=k,
∴2﹣m=k,
∴m+k=2.
一.选择题
1.在平行四边形ABCD中,∠A+∠C=100°,则∠D等于( )
A.50° B.80° C.100° D.130°
2.如图,A,B两地被池塘隔开,小明先在AB外选一点C,然后测出AC,BC的中点M,N.若MN的长为18米,则A,B间的距离是( )
A.9米 B.18米 C.27米 D.36米
3.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.一组对边平行,一组对角相等的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.一组对边平行,一组邻边相等的四边形是平行四边形
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成了一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.③④ C.②③ D.①④
5.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
6.如图,已知平行四边形ABCD中A、C、D三点的坐标,则点B的坐标为( )
A.(﹣3,﹣2) B.(﹣2,﹣2) C.(﹣3,﹣1) D.(﹣2,﹣1)
7.如图所示, ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5, ABCD的周长( )
A.11 B.13 C.16 D.22
8.已知直线a,b,c在同一平面内,且a∥b∥c,a与b之间的距离为5cm,b与c之间的距离为3cm,则a与c之间的距离是( )
A.2cm B.8cm
C.2cm或8cm D.以上都不对
9.如图,平行四边形ABCD中,E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是( )
A.3个 B.4个 C.5个 D.6个
10.如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒2.5cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q也停止运动.设运动时间为t s,开始运动以后,当t为何值时,以P,D,Q,B为顶点的四边形是平行四边形?( )
A. B. C.或 D.或
二.填空题
11.如图,在平行四边形ABCD中,BC=10,DE=4,∠ABC的平分线BE交AD于点E,则AB的长为 .
12.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是 .
13.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,BC=10,CD=6,EF=4,∠AFE=52°,则∠ADC= °.
14.如图, ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是 .
15.如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,连接DF、EF,DE与AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②EF=BD;③四边形ADFE为平行四边形;④AB=4AG.其中正确结论的序号是 .
三.解答题
16.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G,AD=6,EF=3.求AF的长度.
17.如图,四边形ABCD是平行四边形,AC=AD,AE⊥BC,DF⊥AC,垂足分别为E,F.证明AE=DF.
18.如图,已知在 ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,连接AC.求证:四边形ACHE是平行四边形.
19.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,求∠FPE的度数.
20.已知:如图,点O为 ABCD对角线BD的中点,过点O的直线与AB,CD分别相交于点E,F.
求证:
(1)AE=CF;
(2)S四边形AEOD=S四边形CFOB.
21.如图,在 ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.如图,平行四边形ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°.
(1)求证:AB=AE;
(2)若=m(0<m<1),AC=4,连接OE;
①若m=,求平行四边形ABCD的面积;
②设=k,试求k与m满足的关系.
参考答案
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠A+∠D=180°,
∵∠A+∠C=100°,
∴∠A=50°,
∴∠D=180°﹣∠A=130°.
故选:D.
2.解:∵点M,N分别是AC,BC的中点,
∴MN是△ABC的中位线,
∴AB=2MN,
∵MN=18米,
∴AB=36米,
故选:D.
3.解:A、一组对边平行,另一组对边相等的四边形不一定是平行四边形,也可以是等腰梯形,故本选项错误;
B、一组对边平行,一组对角相等的四边形可证出另一组对边也平行,所以该四边形是平行四边形,故本选项正确;
C、一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,故本选项错误;
D、一组对边平行,一组邻角互补的四边形有可能是梯形或平行四边形,故本选项错误;
故选:B.
4.解:∵只有③④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带③④两块碎玻璃,就可以确定平行四边形的大小.
故选:B.
5.解:设BC=x,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴BC+CD=20,
∴CD=20﹣x,
∵AE⊥BC于点E,AF⊥CD于点F,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20﹣x),
解得:x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:D.
6.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵A(﹣1,2),D(3,2),
∴AD=4=BC,
∵C(2,﹣1),
∴B(﹣2,﹣1),
故选:D.
7.解:∵ ABCD的对角线AC,BD相交于点O,
∴OA=OC,AD=BC,AB=CD=5,
∵AE=EB,OE=3,
∴BC=2OE=6,
∴ ABCD的周长=2×(AB+BC)=22.
故选:D.
8.解:如图①,a与c之间的距离为5+3=8(cm);
如图②,a与c之间的距离为5﹣3=2(cm).
∴a与c之间的距离为8cm或2cm.
故选:C.
9.解:∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∵E,F分别AB,CD的中点
∴AE=EB=DF=FC
∴四边形AEFD是平行四边形,四边形EFCB是平行四边形,四边形AFCE是平行四边形,四边形EDFB是平行四边形,四边形GEHF是平行四边形.
∴平行四边形的个数共有6个.
故选:D.
10.解:∵四边形ABCD为平行四边形,
∴PD∥BQ.
若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.
设运动时间为t.
当0<t≤4时,AP=t,PD=10﹣t,CQ=2.5t,BQ=10﹣2.5t,
∴10﹣t=10﹣2.5t,
1.5t=0,
∴t=0(舍去);
当4<t≤8时,AP=t,PD=10﹣t,BQ=2.5t﹣10,
∴10﹣t=2.5t﹣10,
解得:t=;
当8<t≤10时,AP=t,PD=10﹣t,CQ=2.5t﹣20,BQ=30﹣2.5t,
∴10﹣t=30﹣2.5t,
解得:t=(舍去);
综上所述,t的值为时,以P,D,Q,B为顶点的四边形是平行四边形.
故选:B.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10.
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=BC﹣DE=10﹣4=6,
故答案为:6.
12.解:添加条件为:AE=CF,
理由:∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AE=CF,
∴四边形AECF为平行四边形,
故答案为:AE=CF.
13.解:连接BD,
∵点E、F分别是边AB、AD的中点,
∴BD=2EF=8,EF∥BD,
∴∠ADB=∠AFE=52°,
BD2+CD2=100,BC2=100,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=142°,
故答案为:142.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,OB=OD,
∴∠OBE=∠ODF,
∵∠BOE=∠DOF,
∴△BOE≌△DOF(AAS),
∴S阴影=S△AOD=S平行四边形ABCD,
∵AB=3,AC=4,BC=AD=5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴S阴影=S△AOD=S平行四边形ABCD=3,
故答案为:3.
15.解:如图,
连接CF,
∵∠ACB=90°,点F是AB的中点,
∴CF=AF,
∵△ACE是等边三角形,
∴AE=CE,
∴EF⊥AC,
故①正确;
∵△ABD是等边三角形,△ACE是等边三角形,
∴AD=BD,DAB=60°,∠CAE=60°,
∴∠BAE=∠BAC+∠CAE=90°,
∵点F是AB的中点,
∴DF⊥AB,
∴∠DFA=∠BAE=90°,
∴DF∥AE,
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=∠ADC=60°,
∴AD∥BC,
由①知:AC⊥EF,BC⊥AC,
∴EF∥BC,
∴AD∥EF,
∴四边形ADFE是平行四边形,
故③正确;
∵四边形ADFE是平行四边形,
∴AD=EF,
∵AD=BD,
∴EF=BD,故②正确;
∵四边形ADFE是平行四边形,
∴AF=2AG,
∵AD=AB,AB=2AF,
∴AB=4AG,
故④正确;
故答案为:①②③④.
三.解答题
16.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE,
∵AD=6,EF=3,
∴AF+DE=AD﹣EF=3,
∴AF=.
17.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠ACE,
∵AE⊥BC,DF⊥AC,
∴∠AEC=∠AFD=90°,
在△ADF与△ACE中,
,
∴△ADF≌△ACE(AAS),
∴AE=DF.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥CH.
∵点E、F分别是边AD、CD的中点,
∴EF∥AC,即EH∥AC,
∴四边形ACHE是平行四边形.
19.解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=BC,PE=AD,
∵AD=BC,
∴PF=PE,
∴△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°,
∴∠FPE=180°﹣∠PEF﹣∠PFE=180°﹣30°﹣30°=120°.
20.证明:(1)∵点O为对角线BD的中点,
∴OB=OD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠EBO=∠FDO,
在△EBO和△FDO中,
,
∴△EBO≌△FDO(ASA),
∴BE=DF,
∴AB﹣BE=CD﹣DF,
即AE=CF;
(2)∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD=S平行四边形ABCD,
由(1)得:△EBO≌△FDO,
∴S△EBO=S△FDO,
∴S△ABD﹣S△EBO=S△CBD﹣S△FDO,
即S四边形AEOD=S四边形CFOB.
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AB=AE;
(2)解:①∵=m=,
∴AB=BC,
∴AE=BE=BC,
∴AE=CE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠AEB=60°,
∴∠ACE=∠CAE=30°,
∴∠BAC=90°,
当AC=4时,AB=4,
∴平行四边ABCD的面积=2S△ABC=2×AB AC=4×4=16;
②∵四边形ABCD是平行四边形,
∴S△AOD=S△BOC,S△BOC=S△BCD,
∵△ABE是等边三角形,
∴BE=AB=mBC,
∵△BOE的BE边上的高等于△BDC的BC边上的高的一半,底BE等于BC的m倍,
设BC边上的高为h,BC的长为b,
∴S△BCD=×bh,S△OBE=××mb=,
∴S四边形OECD=S△BCD﹣S△OBE=﹣=(﹣)bh,
∵S△AOD=×b=,
∴=(﹣)bh×=k,
∴2﹣m=k,
∴m+k=2.
