8.题型六 综合与实践 课件(共38张PPT)【2024中考数学二轮复习题型分类精讲课件】
文档属性
| 名称 | 8.题型六 综合与实践 课件(共38张PPT)【2024中考数学二轮复习题型分类精讲课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型六
综合与实践
题型精讲课件
( 落实新课标理念)
1. (2023陕西)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若⊙O的半径为4,点P在⊙O上,点M在AB上,连接PM,求线段PM的最小值;
第1题图
解:(1)如图①,连接OP,OM,过点O作OM′⊥AB,
垂足为M′,则OP+PM≥OM.
M′
∵⊙O的半径为4,
∴PM≥OM-4≥OM′-4.
第1题图
M′
(2)如图②所示,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽.已知:∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=6 000 m.根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30 m的圆型环道⊙O;过圆心O,作OM⊥AB,垂足为M,与⊙O交于
点N,连接BN,点P在⊙O上,连接EP.其中,线段BN,
EP及MN是要修的三条道路.要在所修道路BN,EP之
和最短的情况下,使所修道路MN最短,试求此时环道
⊙O的圆心O到AB的距离OM的长.
第1题图
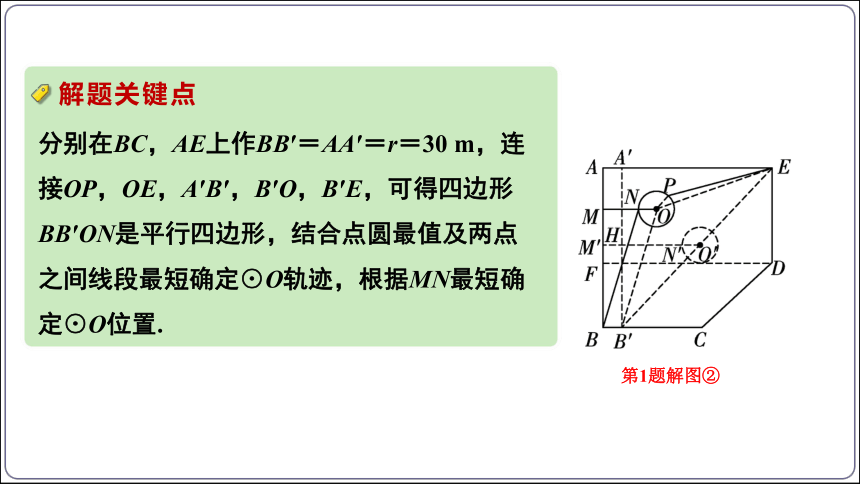
(2)如解图②,分别在BC,AE上作BB′=AA′=r=30 m.
连接A′B′,B′O,OP,OE,B′E,
第1题解图②
∵OM⊥AB,BB′⊥AB,ON=BB′,
∴四边形BB′ON是平行四边形,
∴BN=B′O,
∵B′O+OP+PE≥B′O+OE≥B′E,
∴BN+PE≥B′E-r,
∴当点O在B′E上时,BN+PE取得最小值,
作⊙O′,使圆心O′在B′E上,半径r=30 m,
作O′M′⊥AB,垂足为M′,并与A′B′交于点H,与⊙O′交于点N′,
易证,△B′O′H∽△B′EA′,
第1题解图②
∵⊙O′在矩形AFDE区域内(含边界),
∴当⊙O′与FD相切时,B′H最短,
即B′H=10 000-6 000+30=4 030,
此时,O′H也最短,
∵M′N′=O′H,∴M′N′也最短,
第1题解图②
解题关键点
分别在BC,AE上作BB′=AA′=r=30 m,连接OP,OE,A′B′,B′O,B′E,可得四边形BB′ON是平行四边形,结合点圆最值及两点之间线段最短确定⊙O轨迹,根据MN最短确定⊙O位置.
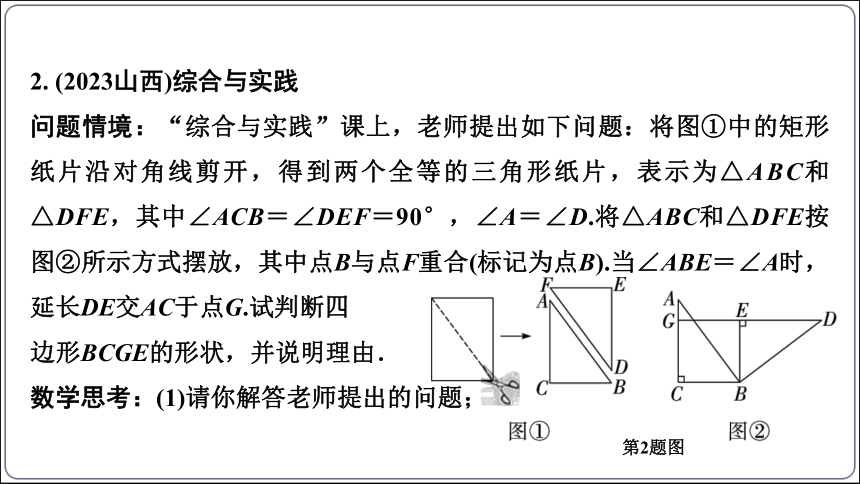
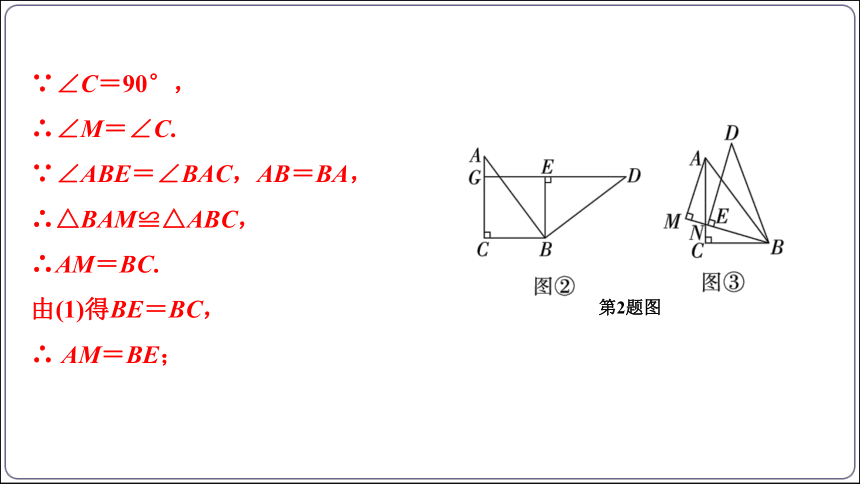
2. (2023山西)综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:将图①中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为△ABC和△DFE,其中∠ACB=∠DEF=90°,∠A=∠D.将△ABC和△DFE按图②所示方式摆放,其中点B与点F重合(标记为点B).当∠ABE=∠A时,延长DE交AC于点G.试判断四
边形BCGE的形状,并说明理由.
数学思考:(1)请你解答老师提出的问题;
第2题图
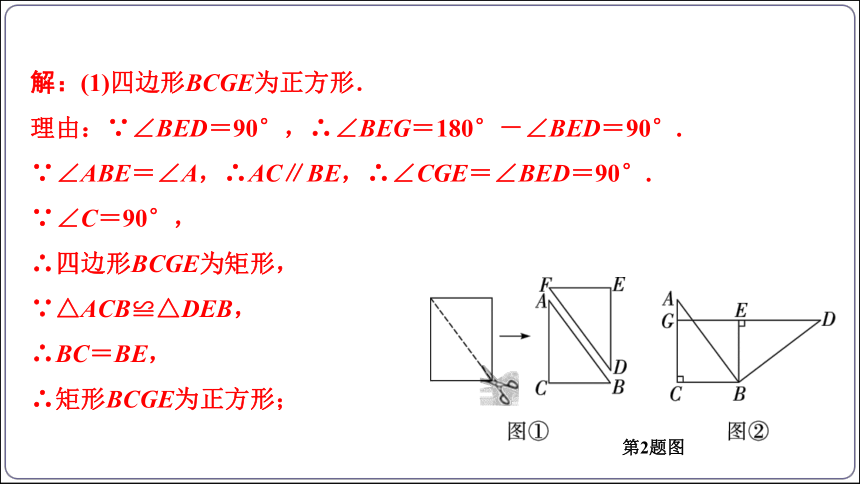
解:(1)四边形BCGE为正方形.
理由:∵∠BED=90°,∴∠BEG=180°-∠BED=90°.
∵∠ABE=∠A,∴AC∥BE,∴∠CGE=∠BED=90°.
∵∠C=90°,
∴四边形BCGE为矩形,
∵△ACB≌△DEB,
∴BC=BE,
∴矩形BCGE为正方形;
第2题图
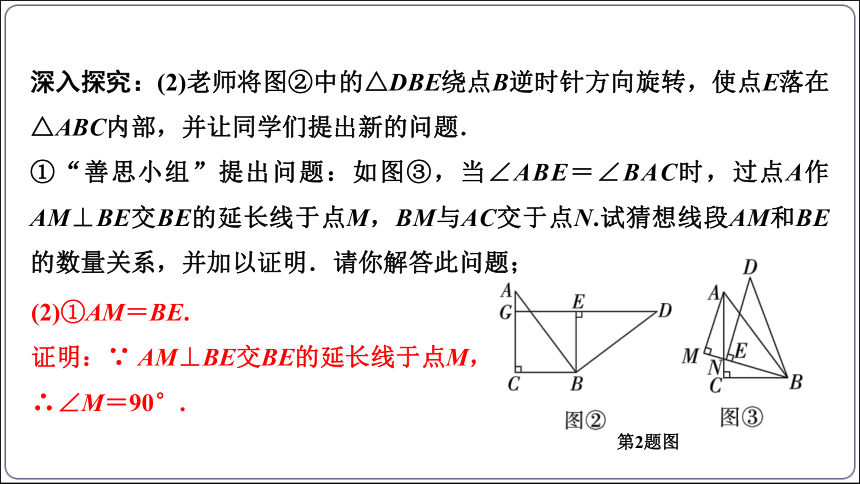
深入探究:(2)老师将图②中的△DBE绕点B逆时针方向旋转,使点E落在△ABC内部,并让同学们提出新的问题.
①“善思小组”提出问题:如图③,当∠ABE=∠BAC时,过点A作AM⊥BE交BE的延长线于点M,BM与AC交于点N.试猜想线段AM和BE的数量关系,并加以证明.请你解答此问题;
第2题图
(2)①AM=BE.
证明:∵ AM⊥BE交BE的延长线于点M,
∴∠M=90°.
第2题图
∵∠C=90°,
∴∠M=∠C.
∵∠ABE=∠BAC,AB=BA,
∴△BAM≌△ABC,
∴AM=BC.
由(1)得BE=BC,
∴ AM=BE;
第2题图
一题多解
(2)②“智慧小组”提出问题:如图④,当∠CBE=∠BAC时,过点A作AH⊥DE于点H,若BC=9,AC=12,求AH的长.请你思考此问题,直接写出结果.
第2题图
如解图,延长AH交BD于点Q,过点Q作QG⊥AC于点G,
第2题解图
第2题解图
3. (2022河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,
得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落
在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图①中一个30°的角:_______;
第3题图
第3题图
【答案】∠ABP或∠PBM或∠MBC或∠BME;(注:任意写出一个即可)
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,
并延长PM交CD于点Q,连接BQ.
①如图②,当点M在EF上时,
∠MBQ=_______°,∠CBQ=_______°;
第3题图
【解法提示】由(1)可知,∠MBC=30°,∵四边形ABCD是正方形,∴BM=BA=BC,∠BMQ=∠C=90°,BQ=BQ,∴Rt△BMQ≌Rt△BCQ(HL),∴∠MBQ=∠CBQ=15°.
15
15
(2)②改变点P在AD上的位置(点P不与点A,D重合),如图③,判断∠MBQ与∠CBQ的数量关系,并说明理由;
第3题图
(2)②∠MBQ=∠CBQ;
理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠C=90°.
由折叠的性质得BM=AB,∠BMP=∠A=90°.
∴∠BMQ=∠C=90°,BM=BC.
∵BQ是公共边,∴Rt△MBQ≌Rt△CBQ(HL).∴∠MBQ=∠CBQ;
(3)拓展应用
在(2)的探究中,已知正方形纸片
ABCD的边长为8 cm,当FQ=1 cm时,
直接写出AP的长.
第3题图
第3题解图
【解法提示】①当点Q在线段CF上时,
如解图①,则DQ=5,
∵BM=BA=BC,∠BMQ=∠C=90°,
BQ=BQ,∴Rt△BMQ≌Rt△BCQ(HL),
∴MQ=CQ=4-1=3,
第3题解图
解题关键点
分点Q在CF和点Q在DF上两种情况分别求解.
4. 综合与实践
数学活动课上,数学老师进行了如下操作:如图①,在正方形ABCD中,点E是边BC上一点,连接AE,以点E为圆心,BE长为半径画弧,交AE于点P,再以点P为圆心,PB长为半径画弧与前弧交于点Q,
连接EQ并延长交CD于点F,连接AF.
(1) 【问题提出】
同学们发现,随着点E的位置不同,∠EAF的度数及EF与
BE,DF的数量关系并没有改变,试猜想∠EAF的度数为
________,EF与BE,DF的数量关系为________;
第4题图
第4题解图①
第4题解图①
解:(1)45°,EF=BE+DF;
第4题图
(2) 【类比探究】
希望小组受(1)的启发,将点E移动到BC的延长线上,如图②,连接AE,并按照数学老师教的尺规作图进行如上操作,其中点F在CD的延长线上,试判断∠EAF的度数及EF与BE,DF之间的数量关系,并加以证明;
(2)∠EAF的度数为45°,EF=BE-DF,
证明:如解图②,延长EF至点Q,
使EQ=BE,连接AQ,
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=∠BAD=90°,
第4题解图②
第4题解图②
第4题解图②
第4题图
(3) 【拓展设问】
如图③,在(2)的条件下,连接BD并延长,交AE于点G,交AF的延长线于点H,若BC=CE=6,求AG的长.
(3)如图③,连接AC,
∵四边形ABCD是正方形,∴∠DAC=∠CBD=45°.
由(2)知,∠EAF=45°,∴∠HAG=∠EBG.
∵∠AGH=∠BGE,∴∠H=∠AEB.
∵∠HAD+∠DAE=∠DAE+∠EAC=45°,
∴∠HAD=∠EAC,∴△HAD∽△EAC,
第4题图
第4题图
5. 综合与实践
问题情境:数学活动课上,王老师出示了一个问题背景:
如图①,在△ABC中,D是边AB上一点,延长CA至点E,BE与CD的延长线相交于点F,且∠BDF=∠ACB.
(1)独立思考:求证:∠ACD=∠ABC;
第5题图
(1)证明:∵∠BDF=∠ADC,∠BDF=∠ACB,
∴∠ADC=∠ACB,
∴∠ABC+∠DCB=∠DCB+∠ACD,
∴∠ACD=∠ABC;
(2)实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新结论,请你证明;“如图②,若CE=BD,点G,H分别在BF,BC上,且BG=CD,∠BGH=∠BCF.求证:BC=CF+GH.”
第5题图
(2)证明:如图,在BC上取一点T,使得BT=CF,连接DT,
T
由(1)知∠ECF=∠CBD,
∵CE=BD,
∴△ECF≌△DBT(SAS),
∴∠CFE=∠BTD,
∵∠CFE=∠FCB+∠CBF,∠BTD=∠FCB+∠CDT,
∴∠CBF=∠CDT,
∵∠BGH=∠BCF,BG=CD,
∴△BGH≌△DCT(ASA),
∴GH=CT,
∴BC=BT+CT=CF+GH;
第5题图
T
(3)问题解决:数学活动小组同学对上述问题进行特殊化研究之后发现,当∠BAC=90°时,若给出△ABC中任意两边长,则图②中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.
“在(2)的条件下,若∠BAC=90°,AB=4,AC=2,求BH的长.”
第5题图
第5题图
解题关键点
由△ACD∽△ABC列比例关系式求出AD的长,在△ACD中求出CD的长,从而可知BG的长,在△ABC中求出BC的长,由△BHG∽△BFC列比例关系式得出BF和BH的数量关系,在△ABE中求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型六
综合与实践
题型精讲课件
( 落实新课标理念)
1. (2023陕西)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若⊙O的半径为4,点P在⊙O上,点M在AB上,连接PM,求线段PM的最小值;
第1题图
解:(1)如图①,连接OP,OM,过点O作OM′⊥AB,
垂足为M′,则OP+PM≥OM.
M′
∵⊙O的半径为4,
∴PM≥OM-4≥OM′-4.
第1题图
M′
(2)如图②所示,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽.已知:∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=6 000 m.根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30 m的圆型环道⊙O;过圆心O,作OM⊥AB,垂足为M,与⊙O交于
点N,连接BN,点P在⊙O上,连接EP.其中,线段BN,
EP及MN是要修的三条道路.要在所修道路BN,EP之
和最短的情况下,使所修道路MN最短,试求此时环道
⊙O的圆心O到AB的距离OM的长.
第1题图
(2)如解图②,分别在BC,AE上作BB′=AA′=r=30 m.
连接A′B′,B′O,OP,OE,B′E,
第1题解图②
∵OM⊥AB,BB′⊥AB,ON=BB′,
∴四边形BB′ON是平行四边形,
∴BN=B′O,
∵B′O+OP+PE≥B′O+OE≥B′E,
∴BN+PE≥B′E-r,
∴当点O在B′E上时,BN+PE取得最小值,
作⊙O′,使圆心O′在B′E上,半径r=30 m,
作O′M′⊥AB,垂足为M′,并与A′B′交于点H,与⊙O′交于点N′,
易证,△B′O′H∽△B′EA′,
第1题解图②
∵⊙O′在矩形AFDE区域内(含边界),
∴当⊙O′与FD相切时,B′H最短,
即B′H=10 000-6 000+30=4 030,
此时,O′H也最短,
∵M′N′=O′H,∴M′N′也最短,
第1题解图②
解题关键点
分别在BC,AE上作BB′=AA′=r=30 m,连接OP,OE,A′B′,B′O,B′E,可得四边形BB′ON是平行四边形,结合点圆最值及两点之间线段最短确定⊙O轨迹,根据MN最短确定⊙O位置.
2. (2023山西)综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:将图①中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为△ABC和△DFE,其中∠ACB=∠DEF=90°,∠A=∠D.将△ABC和△DFE按图②所示方式摆放,其中点B与点F重合(标记为点B).当∠ABE=∠A时,延长DE交AC于点G.试判断四
边形BCGE的形状,并说明理由.
数学思考:(1)请你解答老师提出的问题;
第2题图
解:(1)四边形BCGE为正方形.
理由:∵∠BED=90°,∴∠BEG=180°-∠BED=90°.
∵∠ABE=∠A,∴AC∥BE,∴∠CGE=∠BED=90°.
∵∠C=90°,
∴四边形BCGE为矩形,
∵△ACB≌△DEB,
∴BC=BE,
∴矩形BCGE为正方形;
第2题图
深入探究:(2)老师将图②中的△DBE绕点B逆时针方向旋转,使点E落在△ABC内部,并让同学们提出新的问题.
①“善思小组”提出问题:如图③,当∠ABE=∠BAC时,过点A作AM⊥BE交BE的延长线于点M,BM与AC交于点N.试猜想线段AM和BE的数量关系,并加以证明.请你解答此问题;
第2题图
(2)①AM=BE.
证明:∵ AM⊥BE交BE的延长线于点M,
∴∠M=90°.
第2题图
∵∠C=90°,
∴∠M=∠C.
∵∠ABE=∠BAC,AB=BA,
∴△BAM≌△ABC,
∴AM=BC.
由(1)得BE=BC,
∴ AM=BE;
第2题图
一题多解
(2)②“智慧小组”提出问题:如图④,当∠CBE=∠BAC时,过点A作AH⊥DE于点H,若BC=9,AC=12,求AH的长.请你思考此问题,直接写出结果.
第2题图
如解图,延长AH交BD于点Q,过点Q作QG⊥AC于点G,
第2题解图
第2题解图
3. (2022河南)综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,
得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落
在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图①中一个30°的角:_______;
第3题图
第3题图
【答案】∠ABP或∠PBM或∠MBC或∠BME;(注:任意写出一个即可)
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,
并延长PM交CD于点Q,连接BQ.
①如图②,当点M在EF上时,
∠MBQ=_______°,∠CBQ=_______°;
第3题图
【解法提示】由(1)可知,∠MBC=30°,∵四边形ABCD是正方形,∴BM=BA=BC,∠BMQ=∠C=90°,BQ=BQ,∴Rt△BMQ≌Rt△BCQ(HL),∴∠MBQ=∠CBQ=15°.
15
15
(2)②改变点P在AD上的位置(点P不与点A,D重合),如图③,判断∠MBQ与∠CBQ的数量关系,并说明理由;
第3题图
(2)②∠MBQ=∠CBQ;
理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠C=90°.
由折叠的性质得BM=AB,∠BMP=∠A=90°.
∴∠BMQ=∠C=90°,BM=BC.
∵BQ是公共边,∴Rt△MBQ≌Rt△CBQ(HL).∴∠MBQ=∠CBQ;
(3)拓展应用
在(2)的探究中,已知正方形纸片
ABCD的边长为8 cm,当FQ=1 cm时,
直接写出AP的长.
第3题图
第3题解图
【解法提示】①当点Q在线段CF上时,
如解图①,则DQ=5,
∵BM=BA=BC,∠BMQ=∠C=90°,
BQ=BQ,∴Rt△BMQ≌Rt△BCQ(HL),
∴MQ=CQ=4-1=3,
第3题解图
解题关键点
分点Q在CF和点Q在DF上两种情况分别求解.
4. 综合与实践
数学活动课上,数学老师进行了如下操作:如图①,在正方形ABCD中,点E是边BC上一点,连接AE,以点E为圆心,BE长为半径画弧,交AE于点P,再以点P为圆心,PB长为半径画弧与前弧交于点Q,
连接EQ并延长交CD于点F,连接AF.
(1) 【问题提出】
同学们发现,随着点E的位置不同,∠EAF的度数及EF与
BE,DF的数量关系并没有改变,试猜想∠EAF的度数为
________,EF与BE,DF的数量关系为________;
第4题图
第4题解图①
第4题解图①
解:(1)45°,EF=BE+DF;
第4题图
(2) 【类比探究】
希望小组受(1)的启发,将点E移动到BC的延长线上,如图②,连接AE,并按照数学老师教的尺规作图进行如上操作,其中点F在CD的延长线上,试判断∠EAF的度数及EF与BE,DF之间的数量关系,并加以证明;
(2)∠EAF的度数为45°,EF=BE-DF,
证明:如解图②,延长EF至点Q,
使EQ=BE,连接AQ,
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=∠BAD=90°,
第4题解图②
第4题解图②
第4题解图②
第4题图
(3) 【拓展设问】
如图③,在(2)的条件下,连接BD并延长,交AE于点G,交AF的延长线于点H,若BC=CE=6,求AG的长.
(3)如图③,连接AC,
∵四边形ABCD是正方形,∴∠DAC=∠CBD=45°.
由(2)知,∠EAF=45°,∴∠HAG=∠EBG.
∵∠AGH=∠BGE,∴∠H=∠AEB.
∵∠HAD+∠DAE=∠DAE+∠EAC=45°,
∴∠HAD=∠EAC,∴△HAD∽△EAC,
第4题图
第4题图
5. 综合与实践
问题情境:数学活动课上,王老师出示了一个问题背景:
如图①,在△ABC中,D是边AB上一点,延长CA至点E,BE与CD的延长线相交于点F,且∠BDF=∠ACB.
(1)独立思考:求证:∠ACD=∠ABC;
第5题图
(1)证明:∵∠BDF=∠ADC,∠BDF=∠ACB,
∴∠ADC=∠ACB,
∴∠ABC+∠DCB=∠DCB+∠ACD,
∴∠ACD=∠ABC;
(2)实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新结论,请你证明;“如图②,若CE=BD,点G,H分别在BF,BC上,且BG=CD,∠BGH=∠BCF.求证:BC=CF+GH.”
第5题图
(2)证明:如图,在BC上取一点T,使得BT=CF,连接DT,
T
由(1)知∠ECF=∠CBD,
∵CE=BD,
∴△ECF≌△DBT(SAS),
∴∠CFE=∠BTD,
∵∠CFE=∠FCB+∠CBF,∠BTD=∠FCB+∠CDT,
∴∠CBF=∠CDT,
∵∠BGH=∠BCF,BG=CD,
∴△BGH≌△DCT(ASA),
∴GH=CT,
∴BC=BT+CT=CF+GH;
第5题图
T
(3)问题解决:数学活动小组同学对上述问题进行特殊化研究之后发现,当∠BAC=90°时,若给出△ABC中任意两边长,则图②中所有已经用字母标记的线段长均可求.该小组提出下面的问题,请你解答.
“在(2)的条件下,若∠BAC=90°,AB=4,AC=2,求BH的长.”
第5题图
第5题图
解题关键点
由△ACD∽△ABC列比例关系式求出AD的长,在△ACD中求出CD的长,从而可知BG的长,在△ABC中求出BC的长,由△BHG∽△BFC列比例关系式得出BF和BH的数量关系,在△ABE中求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
