6.题型四 二次函数综合题 类型七~类型八 课件(共62张PPT)【2024中考数学二轮复习题型分类精讲课件】
文档属性
| 名称 | 6.题型四 二次函数综合题 类型七~类型八 课件(共62张PPT)【2024中考数学二轮复习题型分类精讲课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 19:01:53 | ||
图片预览









文档简介
(共62张PPT)
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型四
二次函数综合题
类型7-8
题型精讲课件
类型七 矩形、菱形、正方形存在性问题
三阶 综合提升
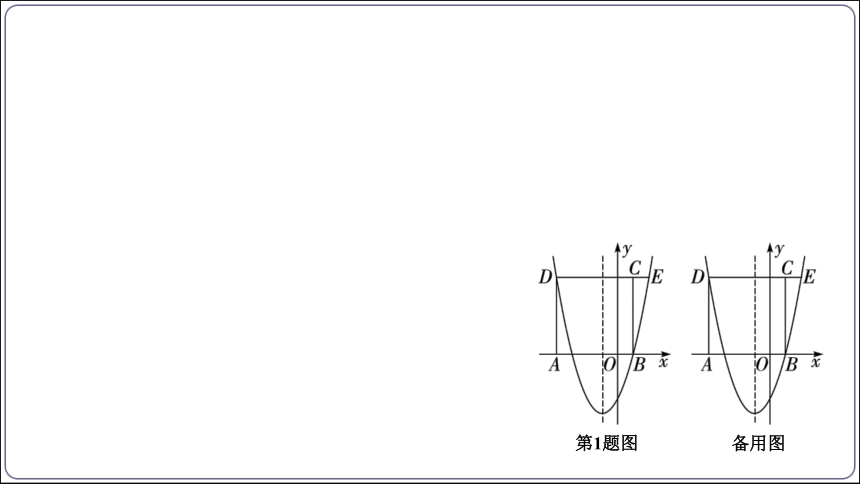
1. (2021恩施州24题节选)如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B、D(-4,5)两点,且与直线DC交于另一点E.
(1)求抛物线的解析式;
第1题图
备用图
解:(1)∵四边形ABCD为正方形,D(-4,5),
∴AD=AB=5,A(-4,0),
∴AO=4,
第1题图
备用图
(2)F为抛物线对称轴上一点,Q为平面直角坐标系中的一点, 是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由.
第1题图
(2)存在.
由(1)可得B(1,0),抛物线解析式为y=x2+2x-3,
则抛物线的对称轴为直线x=-1,
∵点D与点E关于抛物线的对称轴对称,
∴E(2,5),
∴由两点距离公式可得BE2=(1-2)2+(0-5)2=26,
设点F(-1,a),
当以点Q,F,E,B为顶点的四边形是以BE为边的菱形时,
根据菱形的性质可分:
①当EF=BE时,如解图①,
第1题解图①
第1题解图②
2. 如图,已知抛物线y=-x2+2x+c与x轴交A,B两点,与y轴交于点C(0,3),直线y=2x与抛物线相交.
(1)求抛物线的解析式及点A,B的坐标;
第2题图
备用图
解:(1)∵抛物线y=-x2+2x+c与y轴交于点C(0,3),
∴c=3,
∴抛物线的解析式为y=-x2+2x+3.
∵抛物线与x轴交于A,B两点,
∴令y=0,解得x1=-1,x2=3,
∴点A的坐标为(-1,0),点B的坐标为(3,0);
第2题解图
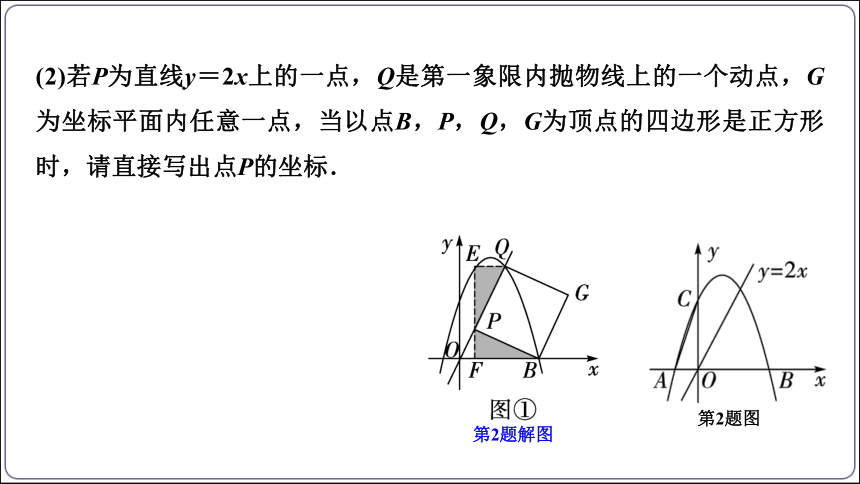
(2)若P为直线y=2x上的一点,Q是第一象限内抛物线上的一个动点,G为坐标平面内任意一点,当以点B,P,Q,G为顶点的四边形是正方形时,请直接写出点P的坐标.
第2题图
第2题解图
第2题解图
第2题解图
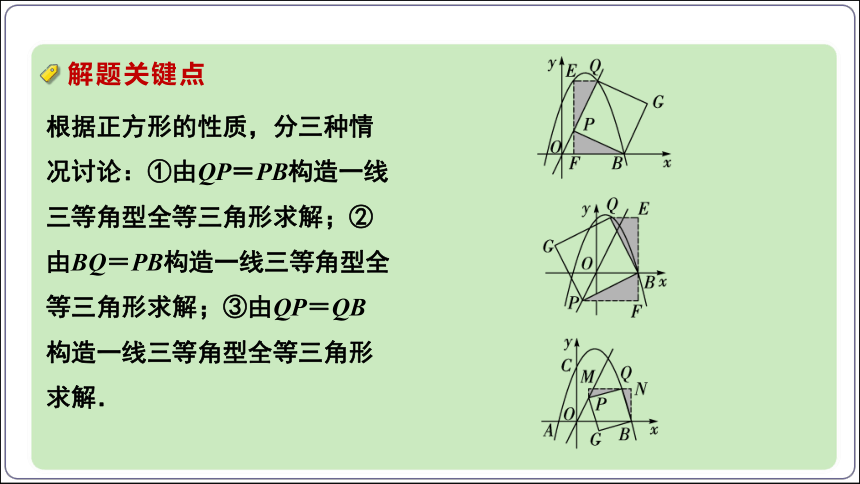
解题关键点
根据正方形的性质,分三种情况讨论:①由QP=PB构造一线三等角型全等三角形求解;②由BQ=PB构造一线三等角型全等三角形求解;③由QP=QB构造一线三等角型全等三角形求解.
3. (2022随州24题12分)如图①,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=-1,且OA=OC,P为抛物线上一动点.
(1)直接写出抛物线的解析式;
第3题图
解:(1)抛物线的解析式为y=-x2-2x+3;
(2)如图②,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;
第3题图
第3题图
Q
第3题图
Q
第3题图
(3)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.
第3题图
备用图
【解法提示】如解图③中,当点N在y轴上时,四边形PMCN是矩形,此时P(-1,4),N(0,4);
第3题解图
第3题解图
第3题解图
4. 如图,抛物线y=-x2+4x-3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
(1)求点D的坐标及直线BC的函数表达式;
第4题图
解:(1)∵y=-x2+4x-3=-(x-2)2+1,∴D(2,1);
把y=0代入y=-x2+4x-3,得0=-x2+4x-3,
解得x1=1,x2=3,
∵点A在点B左侧,
∴A(1,0),B(3,0),把x=0代入y=-x2+4x-3,得y=-3,
∴C(0,-3),
第4题图
(2)如解图①,∵点F在线段BC上,由(1)知,直线BC的函数表达式为
y=x-3,易得B(3,0),
∴设点F(a,a-3),
∵点M在抛物线上,且MF∥y轴,
∴M(a,-a2+4a-3),
∵点M在F上方,
∴MF=-a2+3a,
第4题解图①
(2)点F是线段BC上一点,过点F作y轴的平行线交抛物线于点M,求△BCM面积的最大值;
第4题图
第4题解图①
(3)点P是对称轴上一点,点Q是平面内一点,且点Q纵坐标的值为负数,则以A,C,P,Q为顶点的四边形能否为菱形?若能,直接写出点Q的坐标;若不能,请说明理由.
第4题图
【解法提示】设点P(2,h),
∵A(1,0),C(0,-3),
∴OA=1,OC=3,
∴AC2=32+12=10,
①如解图②,当AP为菱形ACPQ的对角线时,AC=CP,即AC2=CP2,
第4题解图
第4题解图
第4题解图
解题关键点
分三种情况讨论:
①AP为菱形ACPQ的对角线;②AQ为菱形ACQP的对角线;③AC为菱形APCQ的对角线,分别求解.
三阶 综合提升
类型八 与全等、相似有关的问题
(黄冈2考;咸宁2021.24(2))
1. (2023随州24题节选)如图,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直
线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式;
第1题图
备用图
解:(1)抛物线的解析式为
y=-x2+x+2,
直线BC的解析式为y=-x+2;
第1题图
备用图
(2)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
第1题图
第1题图
第1题图
第1题图
第1题图
2. (2022恩施州24题节选)在平面直角坐标系中,O为坐标原点,抛物线y=-x2+c与y轴交于点P(0,4).
(1)直接写出抛物线的解析式;
第2题图
备用图
解:(1)抛物线的解析式为y=-x2+4;
(2)如图,将抛物线y=-x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由;
第2题图
(2)是.理由:抛物线y=-x2+4的顶点坐标为(0,4),
将抛物线y=-x2+4向左平移1个单位长度的抛物线解析式
为y=-(x+1)2+4,顶点为Q(-1,4),
令y=0,则-(x+1)2+4=0,解得x=-3或x=1,
第2题图
(3)直线BC与抛物线y=-x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.
第2题图
第2题图
T
第2题图
T
第2题图
解题关键点
分两种情况:①△TBN∽△ABC,②△NBT∽△ABC分别求解.
3. (2018随州24题12分)如图①,抛物线C1:y=ax2-2ax+c(a<0)与x轴交于A,B两点,与y轴交于点C.已知点A的坐标为(-1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
(1)求出抛物线C1的解析式,并写出点G的坐标;
第3题图
解:(1)∵点A的坐标为(-1,0),
∴OA=1,
又∵OC=3OA,抛物线C1开口向下,且对称轴为直线x=1,
∴点C坐标为(0,3),
第3题图
(2)如图②,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′,B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值;
第3题图
∟
D
∟
D
第3题图
(3)在(2)的条件下,如图③,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1,C2于P,Q两点,试探究在直线y=-1上是否存在点N,使得以P,Q,N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标;若不存在,请说明理由.
第3题图
【解法提示】如解图,延长PQ交直线y=-1于点E,设点M(x,0),N(y,-1),则点P(x,-x2+2x+3),Q(x,-x2+2x+2),则PQ=1,∴AO=PQ,第一种情况,当△AOQ≌△PQN时,只需∠QOA=∠NQP,OQ=QN,
第3题解图
第3题解图
第二种情况当△AOQ≌△QPN时,只需∠QOA=∠QPN,OQ=PN,同第一种情况,易得△OQM≌△PNE,∴OM=PE,QM=NE,即x=x2-2x-4,x2-2x-2=|y-x|,解得x=4,或x=-1(舍去),当点N在E右侧时,y=10,当点N在E左侧时,y=-2,∴M3(4,0),N3(10,-1);M4(4,0),N4(-2,-1).
第3题解图
4. 如图,在平面直角坐标系中,已知抛物线y= x2+bx+c与x轴分别交于A(-1,0),B两点,与y轴交于点C,它的对称轴是直线x
= .
(1)求抛物线的函数表达式及点C的坐标;
第4题图
第4题图
(2)如图,点P为抛物线上一动点,点P的横坐标为m(m>0),连接PC,作∠ACP的平分线交x轴于点D,当线段CD为△OBC的中线时,求点P的坐标;
第4题图
(2)∵CD为△OBC的中线,点B(4,0),
∴点D的坐标为(2,0).
如图,过点D作DG∥AC,交CP的延长线于点G,过点G作GF⊥x轴,垂足为点F,过点C作CH⊥GF,垂足为点H,
∟
G
F
∟
H
∟
G
F
∟
H
第4题图
∵DG∥AC,
∴∠ACD=∠CDG,∴∠DCG=∠CDG,∴CG=DG.
在Rt△DFG中,根据勾股定理,得DG2=DF2+FG2=x2+(2x)2=5x2,
在Rt△CGH中,根据勾股定理,得CG2=CH2+GH2=(2+x)2+(2x-2)2=5x2-4x+8,
由CG2=DG2得5x2-4x+8=5x2,
解得x=2,
∴点G的坐标为(4,-4),
∟
G
F
∟
H
第4题图
∟
G
F
∟
H
第4题图
(3)在(2)的条件下,取BC的中点E,连接AP,在平面内是否存在一点Q,使得△QCE与△ACP全等,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
第4题图
第4题解图
第4题解图
第4题解图
解题关键点
分两种情况:
①∠ACP=∠ECQ,
②∠ACP=∠CEQ分别求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型四
二次函数综合题
类型7-8
题型精讲课件
类型七 矩形、菱形、正方形存在性问题
三阶 综合提升
1. (2021恩施州24题节选)如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B、D(-4,5)两点,且与直线DC交于另一点E.
(1)求抛物线的解析式;
第1题图
备用图
解:(1)∵四边形ABCD为正方形,D(-4,5),
∴AD=AB=5,A(-4,0),
∴AO=4,
第1题图
备用图
(2)F为抛物线对称轴上一点,Q为平面直角坐标系中的一点, 是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由.
第1题图
(2)存在.
由(1)可得B(1,0),抛物线解析式为y=x2+2x-3,
则抛物线的对称轴为直线x=-1,
∵点D与点E关于抛物线的对称轴对称,
∴E(2,5),
∴由两点距离公式可得BE2=(1-2)2+(0-5)2=26,
设点F(-1,a),
当以点Q,F,E,B为顶点的四边形是以BE为边的菱形时,
根据菱形的性质可分:
①当EF=BE时,如解图①,
第1题解图①
第1题解图②
2. 如图,已知抛物线y=-x2+2x+c与x轴交A,B两点,与y轴交于点C(0,3),直线y=2x与抛物线相交.
(1)求抛物线的解析式及点A,B的坐标;
第2题图
备用图
解:(1)∵抛物线y=-x2+2x+c与y轴交于点C(0,3),
∴c=3,
∴抛物线的解析式为y=-x2+2x+3.
∵抛物线与x轴交于A,B两点,
∴令y=0,解得x1=-1,x2=3,
∴点A的坐标为(-1,0),点B的坐标为(3,0);
第2题解图
(2)若P为直线y=2x上的一点,Q是第一象限内抛物线上的一个动点,G为坐标平面内任意一点,当以点B,P,Q,G为顶点的四边形是正方形时,请直接写出点P的坐标.
第2题图
第2题解图
第2题解图
第2题解图
解题关键点
根据正方形的性质,分三种情况讨论:①由QP=PB构造一线三等角型全等三角形求解;②由BQ=PB构造一线三等角型全等三角形求解;③由QP=QB构造一线三等角型全等三角形求解.
3. (2022随州24题12分)如图①,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=-1,且OA=OC,P为抛物线上一动点.
(1)直接写出抛物线的解析式;
第3题图
解:(1)抛物线的解析式为y=-x2-2x+3;
(2)如图②,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;
第3题图
第3题图
Q
第3题图
Q
第3题图
(3)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.
第3题图
备用图
【解法提示】如解图③中,当点N在y轴上时,四边形PMCN是矩形,此时P(-1,4),N(0,4);
第3题解图
第3题解图
第3题解图
4. 如图,抛物线y=-x2+4x-3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
(1)求点D的坐标及直线BC的函数表达式;
第4题图
解:(1)∵y=-x2+4x-3=-(x-2)2+1,∴D(2,1);
把y=0代入y=-x2+4x-3,得0=-x2+4x-3,
解得x1=1,x2=3,
∵点A在点B左侧,
∴A(1,0),B(3,0),把x=0代入y=-x2+4x-3,得y=-3,
∴C(0,-3),
第4题图
(2)如解图①,∵点F在线段BC上,由(1)知,直线BC的函数表达式为
y=x-3,易得B(3,0),
∴设点F(a,a-3),
∵点M在抛物线上,且MF∥y轴,
∴M(a,-a2+4a-3),
∵点M在F上方,
∴MF=-a2+3a,
第4题解图①
(2)点F是线段BC上一点,过点F作y轴的平行线交抛物线于点M,求△BCM面积的最大值;
第4题图
第4题解图①
(3)点P是对称轴上一点,点Q是平面内一点,且点Q纵坐标的值为负数,则以A,C,P,Q为顶点的四边形能否为菱形?若能,直接写出点Q的坐标;若不能,请说明理由.
第4题图
【解法提示】设点P(2,h),
∵A(1,0),C(0,-3),
∴OA=1,OC=3,
∴AC2=32+12=10,
①如解图②,当AP为菱形ACPQ的对角线时,AC=CP,即AC2=CP2,
第4题解图
第4题解图
第4题解图
解题关键点
分三种情况讨论:
①AP为菱形ACPQ的对角线;②AQ为菱形ACQP的对角线;③AC为菱形APCQ的对角线,分别求解.
三阶 综合提升
类型八 与全等、相似有关的问题
(黄冈2考;咸宁2021.24(2))
1. (2023随州24题节选)如图,平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0),B(2,0)和C(0,2),连接BC,点P(m,n)(m>0)为抛物线上一动点,过点P作PN⊥x轴交直
线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式;
第1题图
备用图
解:(1)抛物线的解析式为
y=-x2+x+2,
直线BC的解析式为y=-x+2;
第1题图
备用图
(2)当P点在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
第1题图
第1题图
第1题图
第1题图
第1题图
2. (2022恩施州24题节选)在平面直角坐标系中,O为坐标原点,抛物线y=-x2+c与y轴交于点P(0,4).
(1)直接写出抛物线的解析式;
第2题图
备用图
解:(1)抛物线的解析式为y=-x2+4;
(2)如图,将抛物线y=-x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由;
第2题图
(2)是.理由:抛物线y=-x2+4的顶点坐标为(0,4),
将抛物线y=-x2+4向左平移1个单位长度的抛物线解析式
为y=-(x+1)2+4,顶点为Q(-1,4),
令y=0,则-(x+1)2+4=0,解得x=-3或x=1,
第2题图
(3)直线BC与抛物线y=-x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.
第2题图
第2题图
T
第2题图
T
第2题图
解题关键点
分两种情况:①△TBN∽△ABC,②△NBT∽△ABC分别求解.
3. (2018随州24题12分)如图①,抛物线C1:y=ax2-2ax+c(a<0)与x轴交于A,B两点,与y轴交于点C.已知点A的坐标为(-1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
(1)求出抛物线C1的解析式,并写出点G的坐标;
第3题图
解:(1)∵点A的坐标为(-1,0),
∴OA=1,
又∵OC=3OA,抛物线C1开口向下,且对称轴为直线x=1,
∴点C坐标为(0,3),
第3题图
(2)如图②,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′,B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值;
第3题图
∟
D
∟
D
第3题图
(3)在(2)的条件下,如图③,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1,C2于P,Q两点,试探究在直线y=-1上是否存在点N,使得以P,Q,N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标;若不存在,请说明理由.
第3题图
【解法提示】如解图,延长PQ交直线y=-1于点E,设点M(x,0),N(y,-1),则点P(x,-x2+2x+3),Q(x,-x2+2x+2),则PQ=1,∴AO=PQ,第一种情况,当△AOQ≌△PQN时,只需∠QOA=∠NQP,OQ=QN,
第3题解图
第3题解图
第二种情况当△AOQ≌△QPN时,只需∠QOA=∠QPN,OQ=PN,同第一种情况,易得△OQM≌△PNE,∴OM=PE,QM=NE,即x=x2-2x-4,x2-2x-2=|y-x|,解得x=4,或x=-1(舍去),当点N在E右侧时,y=10,当点N在E左侧时,y=-2,∴M3(4,0),N3(10,-1);M4(4,0),N4(-2,-1).
第3题解图
4. 如图,在平面直角坐标系中,已知抛物线y= x2+bx+c与x轴分别交于A(-1,0),B两点,与y轴交于点C,它的对称轴是直线x
= .
(1)求抛物线的函数表达式及点C的坐标;
第4题图
第4题图
(2)如图,点P为抛物线上一动点,点P的横坐标为m(m>0),连接PC,作∠ACP的平分线交x轴于点D,当线段CD为△OBC的中线时,求点P的坐标;
第4题图
(2)∵CD为△OBC的中线,点B(4,0),
∴点D的坐标为(2,0).
如图,过点D作DG∥AC,交CP的延长线于点G,过点G作GF⊥x轴,垂足为点F,过点C作CH⊥GF,垂足为点H,
∟
G
F
∟
H
∟
G
F
∟
H
第4题图
∵DG∥AC,
∴∠ACD=∠CDG,∴∠DCG=∠CDG,∴CG=DG.
在Rt△DFG中,根据勾股定理,得DG2=DF2+FG2=x2+(2x)2=5x2,
在Rt△CGH中,根据勾股定理,得CG2=CH2+GH2=(2+x)2+(2x-2)2=5x2-4x+8,
由CG2=DG2得5x2-4x+8=5x2,
解得x=2,
∴点G的坐标为(4,-4),
∟
G
F
∟
H
第4题图
∟
G
F
∟
H
第4题图
(3)在(2)的条件下,取BC的中点E,连接AP,在平面内是否存在一点Q,使得△QCE与△ACP全等,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
第4题图
第4题解图
第4题解图
第4题解图
解题关键点
分两种情况:
①∠ACP=∠ECQ,
②∠ACP=∠CEQ分别求解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
