2.题型二 函数的实际应用 课件(共52张PPT)【2024中考数学二轮复习题型分类精讲课件】
文档属性
| 名称 | 2.题型二 函数的实际应用 课件(共52张PPT)【2024中考数学二轮复习题型分类精讲课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 18:56:19 | ||
图片预览










文档简介
(共52张PPT)
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型二
函数的实际应用
题型精讲课件
类型一 折线型函数图象问题
(黄冈3考;孝感2考;咸宁4考)
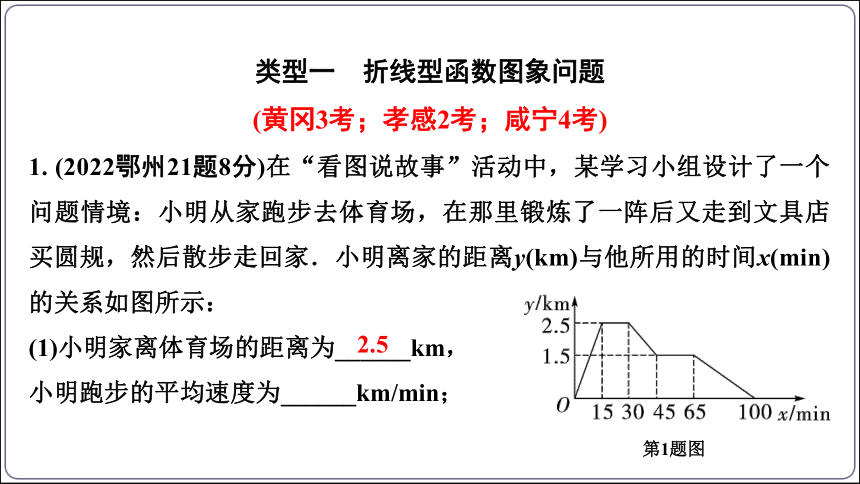
1. (2022鄂州21题8分)在“看图说故事”活动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为______km,
小明跑步的平均速度为______km/min;
第1题图
2.5
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
第1题图
(3)当小明离家2 km时,求他离开家所用的时间.
第1题图
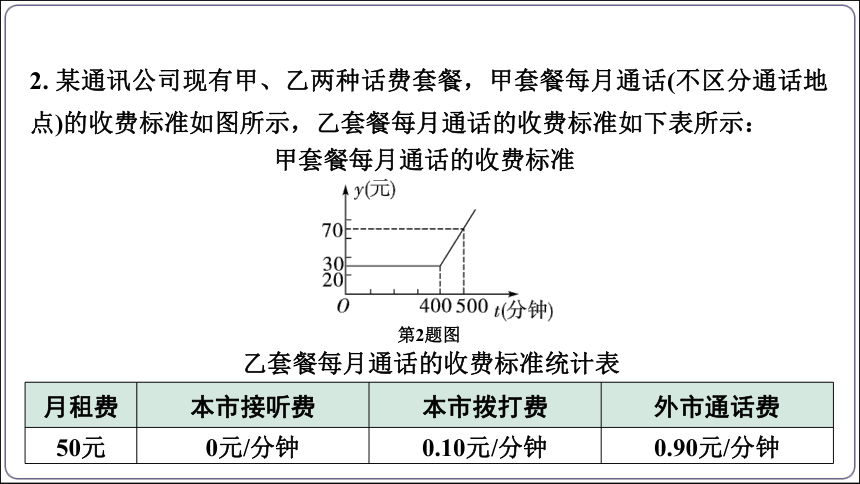
2. 某通讯公司现有甲、乙两种话费套餐,甲套餐每月通话(不区分通话地点)的收费标准如图所示,乙套餐每月通话的收费标准如下表所示:
第2题图
甲套餐每月通话的收费标准
乙套餐每月通话的收费标准统计表
月租费 本市接听费 本市拨打费 外市通话费
50元 0元/分钟 0.10元/分钟 0.90元/分钟
(1)写出甲套餐月通话时间不超过400分钟时应付的话费金额;
第2题图
甲套餐每月通话的收费标准
解:(1)甲套餐通话时间不超过400分钟时应付的话费金额是30元;
(2)求出甲套餐通话时间超过400分钟后,通话费用y1(元)与通话时间t(分钟)之间的函数关系式;
第2题图
甲套餐每月通话的收费标准
(3)王先生由于工作需要,从4月份开始经常去外地出差,每月各种通话时间的比例为本地接听时间∶本地拨打时间∶外地通话时间=2∶1∶1.他想重新办一张卡在出差期间使用,设王先生每月的各种通话时间总和为t(分钟),通话费用为y(元),则王先生选择哪种套餐更划算?请通过计算说明理由.
第2题图
甲套餐每月通话的收费标准
乙套餐每月通话的收费标准统计表
月租费 本市接听费 本市拨打费 外市通话费
50元 0元/分钟 0.10元/分钟 0.90元/分钟
∴当王先生的通话时间总和大于1 200分钟时,选择乙套餐更划算,当通话时间0≤t<1 200时,选择甲套餐更划算,当通话时间t=1 200分钟时,选择两种套餐都一样.
3. 某批发商销售一种大米,有5 kg和10 kg两种包装,其中5 kg
装的大米进行促销活动,其价格y(元/袋)与购买的重量x(kg)之间的函数关系图象如图所示,10 kg装的大米价格为75元/袋.
(1)某商店老板准备购买5 kg装的大米400 kg,需要花费多少元?
第3题图
第3题图
(2)若某超市准备购买1 000 kg大米,其中购买5 kg装的大米不少于600 kg,设购买5 kg装的大米a袋,购买10 kg装的大米b袋.
①求a,b之间的关系式;
(2)①由题意可得5a+10b=1 000,
∴b=100-0.5a,
∵600≤5a≤1 000,
∴120≤a≤200,
∴b=100-0.5a(120≤a≤200);
第3题图
②由于购买量大,该批发商对10 kg装的大米进行优惠:若购买10 kg装的大米超过30袋,则10 kg装的全部打9折,设该超市购买大米的总费用为W元,问如何购买使得总费用W最少?请说明理由.
第3题图
第一种:当120≤a<140,30<b≤40时,
W=40a+0.9×75b=6.25a+6 750,
∵6.25>0,
∴W随a的增大而增大,
∴当a=120,b=40时,W最少,W最少=7 500元;
第二种:当140≤a≤200,0≤b≤30时,
W=40a+75b=2.5a+7 500,
∵2.5>0,
∴W随a的增大而增大,
第3题图
∴当a=140,b=30时,W最少,W最少=7 850元,
综上所述,当a=120,b=40时,W最少,W最少=7 500元,
答:购买5 kg装的大米120袋,10 kg装的大米40袋时,购买总费用最少.
第3题图
4. (2023黄石模拟)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20,x为整数)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:(注:题中x均为整数)
第x天 1 2 3 …
m(kg) 20 24 28 …
第4题图
(1)请分别求出销售单价y(元/kg)与x(天)之间及销售量m(kg)与x(天)之间的函数关系式;
第4题图
第x天 1 2 3 …
m(kg) 20 24 28 …
(2)若规定每天的销售量不超过80 kg,求在销售的第几天时,当天的利润最大,最大利润是多少?
第4题图
(2)设当天的总利润为w元,
当1≤x≤7时,w=(60-18)(4x+16)=168x+672,
∵x=7时,m=4×7+16=44<80,
∵168>0,w随x的增大而增大,
∴此时w取得最大值,最大值为168×7+672=1 848(元);
当8≤x≤20时,w=(-x+58-18)(4x+16)=-4x2+144x+640=
-4(x-18)2+1 936,
若m≤80,即4x+16≤80,则x≤16,
∵-4<0,8≤x≤16时,w随x的增大而增大,
∴当x=16时,w取得最大值,
最大利润为-4×(16-18)2+1 936=1 920(元);
综上所述,每天的销售量不超过80 kg时,
在销售的第16天时,当天的利润最大,最大利润是1 920元;
第4题图
(3)在试销一周后,超市老板决定每销售1千克水果就捐赠a元给养老院,若每天扣除捐赠后的销售利润在第10天达到最大,求a的取值范围.
第4题图
类型二 抛物线型问题
5. 发球机是羽毛球训练中的常用设备,能够按照设定角度发球.小明在羽毛球馆利用发球机进行日常训练,已知发球机发球角度固定,球在运动的过程中其运动轨迹可以近似地看作是抛物线的一部分,建立如图所示的平面直角坐标系,发球机OA将球从点A处发出,在球运动的过程中,球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足y=a(x-h)2+k(a<0),若发球点距离地面的高度为
1 m,球在距发球点水平距离4 m的球网正上方达到
最高点,最高点距离地面5 m.
第5题图
(1)根据以上信息,求羽毛球的竖直高度y与水平距离x之间的函数关系式;
第5题图
(2)这次训练小明站在距离球网2 m的点B处接球,已知小明最大击球高度为2.75 m,若要恰好挥拍击中羽毛球,求至少需要后退的距离.(球拍和球的大小忽略不计)
第5题图
6. (2023武汉22题10分)某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离x(单位:m)、飞行高度y(单位:m)随飞行时间t(单位:s)变化的数据如下表.
飞行时间t/s 0 2 4 6 8 …
飞行水平距离x/m 0 10 20 30 40 …
飞行高度y/m 0 22 40 54 64 …
探究发现 x与t,y与t之间的数量关系可以用我们已学过的函数来描述,直接写出x关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围).
问题解决 如图,活动小组在水平安全线上A处设置一个高度可以变化的发射平台试飞该航模飞机,根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0 m,求飞机落到安全线时飞行的水平距离;
第6题图
(2)在安全线上设置回收区域MN,AM=125 m,MN=5 m.若飞机落到MN内(不包括端点M,N),求发射平台相对于安全线的高度的变化范围.
第6题图
(2)设发射平台相对于安全线的高度为n m, 飞机相对于安全线的飞行高度y′=- t2+12t+n,
∵125∴125<5t<130,∴25在y′=- t2+12t+n中,
当t=25,y′=0时,n=12.5;
当t=26,y′=0时,n=26.
∴12.5答:发射平台相对于安全线的高度的变化范围是大于12.5 m且小于26 m.
第6题图
7. 如图是身高为1.75 m的小明在距篮筐4 m处跳起投篮的路线示意图,篮球运行轨迹可近似看作抛物线的一部分,球在小明头顶上方0.25 m的A处出手,在距离篮筐水平距离为1.5 m处达到最大高度3.5 m,最终投入篮筐所在的B处.以小明起跳点O为原点,建立如图所示的平面直角坐标系.
(1)求篮球运行轨迹所在抛物线的表达式;
第7题图
解:(1)由题意知,抛物线的顶点坐标为(2.5,3.5),
∴设抛物线的表达式为y=a(x-2.5)2+3.5(a≠0),
由题图知图象过点B(4,3.05),
代入抛物线的表达式得,a(4-2.5)2+3.5=3.05,
解得a=-0.2,
∴y=-0.2(x-2.5)2+3.5,
即抛物线的表达式为y=-0.2x2+x+2.25;
第7题图
(2)当小明不起跳直接投篮时,篮球运动的抛物线形状与跳起投篮时相同.若他想投中篮筐,则应该向前走多远?
第7题图
(2)设球出手时,小明跳离地面的高度为h m,
则球出手时,球的高度为h+1.75+0.25=(h+2)m.
∵抛物线过点A,
∴h+2=2.25,解得h=0.25,
∴球出手时,小明跳离地面的高度是0.25 m.
∵当小明不起跳直接投篮时,
篮球运动的抛物线形状与跳起投篮时相同,
∴小明不起跳直接投篮时,
篮球运动的抛物线的表达式为y+0.25=-0.2(x-2.5)2+3.5,
∴y=-0.2(x-2.5)2+3.25,
当y=3.05时,-0.2(x-2.5)2+3.25=3.05,解得x1=3.5,x2=1.5,
∴4-3.5=0.5 m,4-1.5=2.5 m.
答:若小明想投中篮筐,则应该向前走0.5 m或2.5 m.
第7题图
8. (2022台州)如图①,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图②,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3 m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2 m,高出喷
水口0.5 m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5 m.
①求上边缘抛物线的函数解析式,并求喷出水的最大射程OC;
第8题图
解:(1)①如解图①,由题意得A(2,2)是上边缘抛物线的顶点,
设y=a(x-2)2+2.
∵抛物线经过点(0,1.5),
∴1.5=4a+2,
∴a=- ,
∴上边缘抛物线的函数解析式为y=- (x-2)2+2.
当y=0时,- (x-2)2+2=0,
∴x1=6,x2=-2(舍去),
∴喷出水的最大射程OC为6 m;
第8题解图①
②求下边缘抛物线与x轴的正半轴交点B的坐标;
第8题图
②∵对称轴为直线x=2,
∴点(0,1.5)的对称点的坐标为(4,1.5),
∴下边缘抛物线是由上边缘抛物线向左
平移4 m得到的,
即点B是由点C向左平移4 m得到,
则点B的坐标为(2,0);
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
第8题图
第8题解图②
第8题解图②
(2)若EF=1 m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
第8题图
类型三 纯文字型问题
(黄冈2考;孝感2021.22;咸宁2考)
9. 为激发学生爱科学、学科学的热情,某校计划用14 400元购买若干台无人机,经过与经销商议价,每台无人机按标价的九折销售,可购买数量比打折前多2台.
(1)求无人机打折后的单价;
解:(1)设打折前无人机的单价为x元,
由题意可得 =2,
解得x=800,
经检验,x=800是原方程的解,且符合实际意义,
∴800×0.9=720(元),
答:无人机打折后的单价为720元;
(2)为了让学生更容易掌握无人机的操作,学校决定增购“模拟器”让学生先在电脑上熟练操作.已知每台“模拟器”售价为300元,该校计划购买无人机和“模拟器”共45台,且无人机的数量不超过“模拟器”数量的一半.请问该校最多还需要添加多少预算?
(2)设总花费为w元,购买无人机m台,则购买“模拟器”(45-m)台,
由题意可得m≤ (45-m),
解得m≤15,
w=720m+300(45-m)=420m+13 500.
∵420>0,
∴w随m的增大而增大,
∴当m=15时,w有最大值,w最大=420×15+13 500=19 800,
19 800-14 400=5 400(元).
答:该校最多还需要添加5 400元的预算.
10. (2023黄冈模拟)某市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为:y=
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成本是18元/千克,每天的利润是W元(利润=销售收入-成本).
(1)m=________,n=________;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(2)由题可知第x天的销售量为20+4(x-1)=4x+16,
当1≤x<20时,
W=(4x+16)(- x+38-18)=-2x2+72x+320=-2(x-18)2+968,
∵-2<0,
∴当x=18时,W最大=968,
当20≤x≤30时,W=(4x+16)(25-18)=28x+112.
∵28>0,
∴W随x的增大而增大,
∴当x=30时,W最大=952.
∵968>952,
∴当x=18时,W最大=968.
答:销售蓝莓第18天时,当天利润最大,最大利润为968元;
(3)在销售蓝莓的前20天中(不包含第20天),当天利润不低于870元的共有多少天?
(3)当1≤x<20时,令-2x2+72x+320=870,
解得x1=25,x2=11,
∵抛物线W=-2x2+72x+320的开口向下,
∴11≤x≤25时,W≥870,∴11≤x<20.
∵x为正整数,
∴有9天利润不低于870元,
∴当天利润不低于870元的天数共有9天.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
中考数学
二轮复习课件
人教版
2024中考数学二轮复习题型分类精讲课件
题型二
函数的实际应用
题型精讲课件
类型一 折线型函数图象问题
(黄冈3考;孝感2考;咸宁4考)
1. (2022鄂州21题8分)在“看图说故事”活动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)小明家离体育场的距离为______km,
小明跑步的平均速度为______km/min;
第1题图
2.5
(2)当15≤x≤45时,请直接写出y关于x的函数表达式;
第1题图
(3)当小明离家2 km时,求他离开家所用的时间.
第1题图
2. 某通讯公司现有甲、乙两种话费套餐,甲套餐每月通话(不区分通话地点)的收费标准如图所示,乙套餐每月通话的收费标准如下表所示:
第2题图
甲套餐每月通话的收费标准
乙套餐每月通话的收费标准统计表
月租费 本市接听费 本市拨打费 外市通话费
50元 0元/分钟 0.10元/分钟 0.90元/分钟
(1)写出甲套餐月通话时间不超过400分钟时应付的话费金额;
第2题图
甲套餐每月通话的收费标准
解:(1)甲套餐通话时间不超过400分钟时应付的话费金额是30元;
(2)求出甲套餐通话时间超过400分钟后,通话费用y1(元)与通话时间t(分钟)之间的函数关系式;
第2题图
甲套餐每月通话的收费标准
(3)王先生由于工作需要,从4月份开始经常去外地出差,每月各种通话时间的比例为本地接听时间∶本地拨打时间∶外地通话时间=2∶1∶1.他想重新办一张卡在出差期间使用,设王先生每月的各种通话时间总和为t(分钟),通话费用为y(元),则王先生选择哪种套餐更划算?请通过计算说明理由.
第2题图
甲套餐每月通话的收费标准
乙套餐每月通话的收费标准统计表
月租费 本市接听费 本市拨打费 外市通话费
50元 0元/分钟 0.10元/分钟 0.90元/分钟
∴当王先生的通话时间总和大于1 200分钟时,选择乙套餐更划算,当通话时间0≤t<1 200时,选择甲套餐更划算,当通话时间t=1 200分钟时,选择两种套餐都一样.
3. 某批发商销售一种大米,有5 kg和10 kg两种包装,其中5 kg
装的大米进行促销活动,其价格y(元/袋)与购买的重量x(kg)之间的函数关系图象如图所示,10 kg装的大米价格为75元/袋.
(1)某商店老板准备购买5 kg装的大米400 kg,需要花费多少元?
第3题图
第3题图
(2)若某超市准备购买1 000 kg大米,其中购买5 kg装的大米不少于600 kg,设购买5 kg装的大米a袋,购买10 kg装的大米b袋.
①求a,b之间的关系式;
(2)①由题意可得5a+10b=1 000,
∴b=100-0.5a,
∵600≤5a≤1 000,
∴120≤a≤200,
∴b=100-0.5a(120≤a≤200);
第3题图
②由于购买量大,该批发商对10 kg装的大米进行优惠:若购买10 kg装的大米超过30袋,则10 kg装的全部打9折,设该超市购买大米的总费用为W元,问如何购买使得总费用W最少?请说明理由.
第3题图
第一种:当120≤a<140,30<b≤40时,
W=40a+0.9×75b=6.25a+6 750,
∵6.25>0,
∴W随a的增大而增大,
∴当a=120,b=40时,W最少,W最少=7 500元;
第二种:当140≤a≤200,0≤b≤30时,
W=40a+75b=2.5a+7 500,
∵2.5>0,
∴W随a的增大而增大,
第3题图
∴当a=140,b=30时,W最少,W最少=7 850元,
综上所述,当a=120,b=40时,W最少,W最少=7 500元,
答:购买5 kg装的大米120袋,10 kg装的大米40袋时,购买总费用最少.
第3题图
4. (2023黄石模拟)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20,x为整数)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:(注:题中x均为整数)
第x天 1 2 3 …
m(kg) 20 24 28 …
第4题图
(1)请分别求出销售单价y(元/kg)与x(天)之间及销售量m(kg)与x(天)之间的函数关系式;
第4题图
第x天 1 2 3 …
m(kg) 20 24 28 …
(2)若规定每天的销售量不超过80 kg,求在销售的第几天时,当天的利润最大,最大利润是多少?
第4题图
(2)设当天的总利润为w元,
当1≤x≤7时,w=(60-18)(4x+16)=168x+672,
∵x=7时,m=4×7+16=44<80,
∵168>0,w随x的增大而增大,
∴此时w取得最大值,最大值为168×7+672=1 848(元);
当8≤x≤20时,w=(-x+58-18)(4x+16)=-4x2+144x+640=
-4(x-18)2+1 936,
若m≤80,即4x+16≤80,则x≤16,
∵-4<0,8≤x≤16时,w随x的增大而增大,
∴当x=16时,w取得最大值,
最大利润为-4×(16-18)2+1 936=1 920(元);
综上所述,每天的销售量不超过80 kg时,
在销售的第16天时,当天的利润最大,最大利润是1 920元;
第4题图
(3)在试销一周后,超市老板决定每销售1千克水果就捐赠a元给养老院,若每天扣除捐赠后的销售利润在第10天达到最大,求a的取值范围.
第4题图
类型二 抛物线型问题
5. 发球机是羽毛球训练中的常用设备,能够按照设定角度发球.小明在羽毛球馆利用发球机进行日常训练,已知发球机发球角度固定,球在运动的过程中其运动轨迹可以近似地看作是抛物线的一部分,建立如图所示的平面直角坐标系,发球机OA将球从点A处发出,在球运动的过程中,球的竖直高度y(单位:m)与水平距离x(单位:m)近似满足y=a(x-h)2+k(a<0),若发球点距离地面的高度为
1 m,球在距发球点水平距离4 m的球网正上方达到
最高点,最高点距离地面5 m.
第5题图
(1)根据以上信息,求羽毛球的竖直高度y与水平距离x之间的函数关系式;
第5题图
(2)这次训练小明站在距离球网2 m的点B处接球,已知小明最大击球高度为2.75 m,若要恰好挥拍击中羽毛球,求至少需要后退的距离.(球拍和球的大小忽略不计)
第5题图
6. (2023武汉22题10分)某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离x(单位:m)、飞行高度y(单位:m)随飞行时间t(单位:s)变化的数据如下表.
飞行时间t/s 0 2 4 6 8 …
飞行水平距离x/m 0 10 20 30 40 …
飞行高度y/m 0 22 40 54 64 …
探究发现 x与t,y与t之间的数量关系可以用我们已学过的函数来描述,直接写出x关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围).
问题解决 如图,活动小组在水平安全线上A处设置一个高度可以变化的发射平台试飞该航模飞机,根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0 m,求飞机落到安全线时飞行的水平距离;
第6题图
(2)在安全线上设置回收区域MN,AM=125 m,MN=5 m.若飞机落到MN内(不包括端点M,N),求发射平台相对于安全线的高度的变化范围.
第6题图
(2)设发射平台相对于安全线的高度为n m, 飞机相对于安全线的飞行高度y′=- t2+12t+n,
∵125
当t=25,y′=0时,n=12.5;
当t=26,y′=0时,n=26.
∴12.5
第6题图
7. 如图是身高为1.75 m的小明在距篮筐4 m处跳起投篮的路线示意图,篮球运行轨迹可近似看作抛物线的一部分,球在小明头顶上方0.25 m的A处出手,在距离篮筐水平距离为1.5 m处达到最大高度3.5 m,最终投入篮筐所在的B处.以小明起跳点O为原点,建立如图所示的平面直角坐标系.
(1)求篮球运行轨迹所在抛物线的表达式;
第7题图
解:(1)由题意知,抛物线的顶点坐标为(2.5,3.5),
∴设抛物线的表达式为y=a(x-2.5)2+3.5(a≠0),
由题图知图象过点B(4,3.05),
代入抛物线的表达式得,a(4-2.5)2+3.5=3.05,
解得a=-0.2,
∴y=-0.2(x-2.5)2+3.5,
即抛物线的表达式为y=-0.2x2+x+2.25;
第7题图
(2)当小明不起跳直接投篮时,篮球运动的抛物线形状与跳起投篮时相同.若他想投中篮筐,则应该向前走多远?
第7题图
(2)设球出手时,小明跳离地面的高度为h m,
则球出手时,球的高度为h+1.75+0.25=(h+2)m.
∵抛物线过点A,
∴h+2=2.25,解得h=0.25,
∴球出手时,小明跳离地面的高度是0.25 m.
∵当小明不起跳直接投篮时,
篮球运动的抛物线形状与跳起投篮时相同,
∴小明不起跳直接投篮时,
篮球运动的抛物线的表达式为y+0.25=-0.2(x-2.5)2+3.5,
∴y=-0.2(x-2.5)2+3.25,
当y=3.05时,-0.2(x-2.5)2+3.25=3.05,解得x1=3.5,x2=1.5,
∴4-3.5=0.5 m,4-1.5=2.5 m.
答:若小明想投中篮筐,则应该向前走0.5 m或2.5 m.
第7题图
8. (2022台州)如图①,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图②,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3 m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2 m,高出喷
水口0.5 m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5 m.
①求上边缘抛物线的函数解析式,并求喷出水的最大射程OC;
第8题图
解:(1)①如解图①,由题意得A(2,2)是上边缘抛物线的顶点,
设y=a(x-2)2+2.
∵抛物线经过点(0,1.5),
∴1.5=4a+2,
∴a=- ,
∴上边缘抛物线的函数解析式为y=- (x-2)2+2.
当y=0时,- (x-2)2+2=0,
∴x1=6,x2=-2(舍去),
∴喷出水的最大射程OC为6 m;
第8题解图①
②求下边缘抛物线与x轴的正半轴交点B的坐标;
第8题图
②∵对称轴为直线x=2,
∴点(0,1.5)的对称点的坐标为(4,1.5),
∴下边缘抛物线是由上边缘抛物线向左
平移4 m得到的,
即点B是由点C向左平移4 m得到,
则点B的坐标为(2,0);
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
第8题图
第8题解图②
第8题解图②
(2)若EF=1 m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
第8题图
类型三 纯文字型问题
(黄冈2考;孝感2021.22;咸宁2考)
9. 为激发学生爱科学、学科学的热情,某校计划用14 400元购买若干台无人机,经过与经销商议价,每台无人机按标价的九折销售,可购买数量比打折前多2台.
(1)求无人机打折后的单价;
解:(1)设打折前无人机的单价为x元,
由题意可得 =2,
解得x=800,
经检验,x=800是原方程的解,且符合实际意义,
∴800×0.9=720(元),
答:无人机打折后的单价为720元;
(2)为了让学生更容易掌握无人机的操作,学校决定增购“模拟器”让学生先在电脑上熟练操作.已知每台“模拟器”售价为300元,该校计划购买无人机和“模拟器”共45台,且无人机的数量不超过“模拟器”数量的一半.请问该校最多还需要添加多少预算?
(2)设总花费为w元,购买无人机m台,则购买“模拟器”(45-m)台,
由题意可得m≤ (45-m),
解得m≤15,
w=720m+300(45-m)=420m+13 500.
∵420>0,
∴w随m的增大而增大,
∴当m=15时,w有最大值,w最大=420×15+13 500=19 800,
19 800-14 400=5 400(元).
答:该校最多还需要添加5 400元的预算.
10. (2023黄冈模拟)某市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为:y=
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成本是18元/千克,每天的利润是W元(利润=销售收入-成本).
(1)m=________,n=________;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(2)由题可知第x天的销售量为20+4(x-1)=4x+16,
当1≤x<20时,
W=(4x+16)(- x+38-18)=-2x2+72x+320=-2(x-18)2+968,
∵-2<0,
∴当x=18时,W最大=968,
当20≤x≤30时,W=(4x+16)(25-18)=28x+112.
∵28>0,
∴W随x的增大而增大,
∴当x=30时,W最大=952.
∵968>952,
∴当x=18时,W最大=968.
答:销售蓝莓第18天时,当天利润最大,最大利润为968元;
(3)在销售蓝莓的前20天中(不包含第20天),当天利润不低于870元的共有多少天?
(3)当1≤x<20时,令-2x2+72x+320=870,
解得x1=25,x2=11,
∵抛物线W=-2x2+72x+320的开口向下,
∴11≤x≤25时,W≥870,∴11≤x<20.
∵x为正整数,
∴有9天利润不低于870元,
∴当天利润不低于870元的天数共有9天.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
