2024年中考数学苏科版二轮复习高频考点突破课件第11章 一元一次不等式(35张ppt)
文档属性
| 名称 | 2024年中考数学苏科版二轮复习高频考点突破课件第11章 一元一次不等式(35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
第11章 一元一次不等式
高频考点突破
考点一 不等式的基本性质
典例1 若x<y,则下列结论中,成立的是( )
A. x+2>y+2 B. -2x<-2y
C. 3x>3y D. 1-x>1-y
思路导引 直接根据不等式的基本性质逐项进行判别.
规范解答 A中,由x<y,可得x+2<y+2,原变形错误,故A不符合题
意.B中,由x<y,可得-2x>-2y,原变形错误,故B不符合题意.C
中,由x<y,可得3x<3y,原变形错误,故C不符合题意.D中,由x<
y,可得1-x>1-y,原变形正确,故D符合题意.故选D.
方法归纳
解不等式的方法
运用不等式的基本性质解决问题的关键在于熟练掌握不等式的基
本性质.特别要注意的是不等式的基本性质2中,不等式的两边都乘(或
除以)同一个负数,不等号的方向改变.
现学活用
1. 已知a>b,则下列变形中,错误的是( B )
A. a-1>b-1
B. 2a<2b
C. -2a+3<-2b+3
D. -5a<-5b
B
2. 若x+y=1,y≤2,则x的取值范围是 .
x≥-1
典例2 若x<y,且(a-3)x>(a-3)y,则a的取值范围是( )
A. a<3 B. a>3 C. a≥3 D. a≤3
思路导引 先比较所给的两个不等式,根据不等式的两边都乘a-3后,
不等号的方向变化,再利用不等式的性质确定a-3与0的大小关系,从
而解决问题.
规范解答 因为x<y,且(a-3)x>(a-3)y,所以a-3<0.所以a<
3.故选A.
现学活用
3. 已知关于x的不等式(a-1)x>1,可化为x<,试化简|1-a|
-|a-2|,正确的结果是 .
-1
考点二 不等式(组)的解集
典例3 已知a、b为常数.若ax+b>0的解集是x<,则bx-a<0的解集
是 .
思路导引 根据ax+b>0的解集是x<,可得a<0,且-=,判断b的
正负性,从而通过解不等式来解决问题.
规范解答 因为ax+b>0的解集是x<,所以a<0,-=,即a=-
3b.所以b>0.所以解不等式bx-a<0,即bx+3b<0,得x<-3.故填x<
-3.
易错警示
不能确定其中隐含条件导致错误
解答这类问题时,往往会出现不能从所给不等式的解集中挖掘字
母系数隐含的取值范围,导致解题错误,需要比较、分析不等式变形
前后不等号方向的变化,来确定字母的取值范围,进而利用隐含的字
母系数之间的数量关系求得不等式的解集.
现学活用
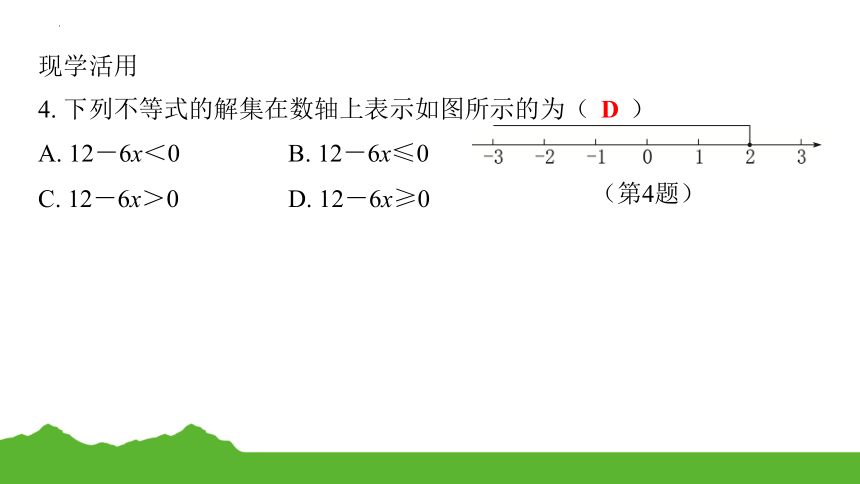
4. 下列不等式的解集在数轴上表示如图所示的为( D )
A. 12-6x<0 B. 12-6x≤0
C. 12-6x>0 D. 12-6x≥0
(第4题)
D
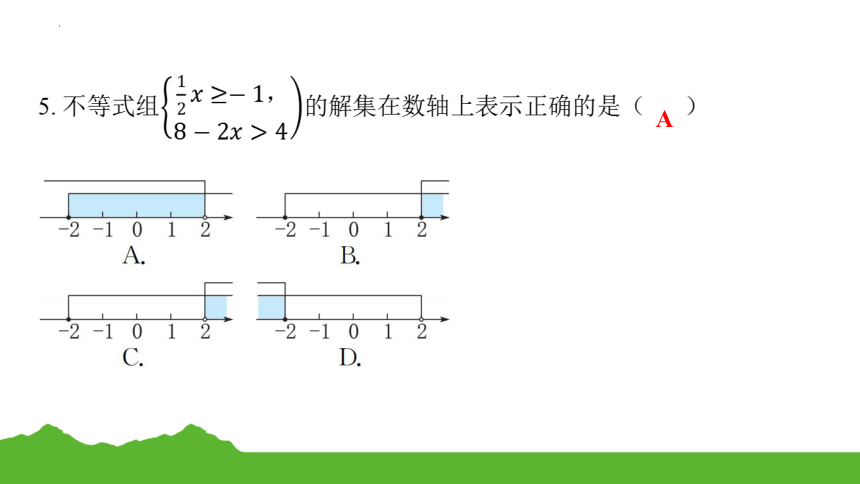
5. 不等式组的解集在数轴上表示正确的是( A )
A
考点三 解不等式(组)
典例4 (2023·湖州)解一元一次不等式组
思路导引 先解不等式组中的每一个不等式,再求它们的公共部分.
规范解答 解不等式①,得x>-1.
解不等式②,得x<2.
所以原不等式组的解集是-1<x<2.
现学活用
6. (1) 解不等式-1<,并把它的解集在数轴上表示出来.
解:该不等式的解集为x>-2.在数轴上表示不等式的解集如图所示.
(2) 解不等式组:
解:不等式组的解集为-1≤x<5.
(第6题答案)
典例5 解不等式组并写出它的正整数解.
思路导引 首先解每个不等式,两个不等式的解集的公共部分就是不等
式组的解集,然后确定解集中的正整数解即可.
规范解答 解x-3(x-2)<6,得x>0.
解x-1<,得x<4.
所以不等式组的解集是0<x<4.
所以原不等式组的正整数解是x=1、2、3.
现学活用
7. 求不等式≤-1的正整数解.
解:该不等式的解集为x≤2.所以原不等式的正整数解为x=1、2.
考点四 运用不等式组的解集解题
典例6 若关于x的不等式组无解,则a的取值范围是
( )
A. a>2 B. a≥2
C. 1<a≤2 D. 1≤a<2
思路导引 先分别表示出不等式组中两个不等式的解集,再由不等式组
的解集,确定出a的取值范围即可.
规范解答 整理不等式组,得由不等式组无解,得a≥2.故选B.
易错警示
不能逆用不等式的解集确定字母的取值范围
解答这类问题时,往往会出现确定范围不全或扩大的错误,究其
原因,是不能根据条件中不等式的解集或特殊整数解的情形,逆用不
等式的解集确定字母的取值范围.
现学活用
8. 已知整式3的值为P.
(1) 当m=5时,求P的值.
解:(1) 因为m=5,所以3=1-3m=1-3×5=-14.因为P=3,所以P=-14.
(2) 若某个关于x的不等式的解集如图所示,P为该不等式的一个解,
求m的负整数值.
解:(2) 因为P=3,所以由
题图,可得3(-m)≤5.所以m≥-.
所以m的负整数值为-1.
(第8题)
解:(3) 由题意,得解不等式②,
得x≥-3m.因为关于x的不等式组恰有两个整数解,
所以不等式组的解集为-3m≤x<1.所以不等式组的整数解是
x=0、-1.所以-2<-3m≤-1.所以≤m<.
(3) 关于x的不等式组恰有两个整数解,求m的取值范围.
考点五 运用不等式解决实际问题
典例7 学校准备为在“航天比赛”活动中获奖的学生购买奖品.已知在
商场购买3个甲种奖品和2个乙种奖品共需120元,其中甲种奖品的单价
是乙种奖品单价的2倍.
(1) 求甲、乙两种奖品的单价.
(2) 学校计划购买甲、乙两种奖品共80个,且此次购买奖品的费用不
超过1500元.正逢商场促销,所有商品一律打8折销售,则学校在商场最
多能购买多少个甲种奖品?
思路导引 (1) 设甲种奖品的单价为x元,乙种奖品的单价为y元,根
据“购买3个甲种奖品和2个乙种奖品共需120元”“甲种奖品的单价是
乙种奖品单价的2倍”,即可得出关于x、y的二元一次方程组,解之即
可.(2) 设学校在商场购买m个甲种奖品,则购买(80-m)个乙种奖
品,根据总价=单价×数量,结合此次购买奖品的费用不超过1500元,
即可得出关于m的一元一次不等式,解之取其中的最大值即可.
规范解答 (1) 设甲种奖品的单价为x元,乙种奖品的单价为y元.
由题意,得解得
所以甲种奖品的单价为30元,乙种奖品的单价为15元.
(2) 设学校在商场购买m个甲种奖品,则购买(80-m)个乙种奖品.
由题意,得30×0.8m+15×0.8(80-m)≤1500,解得m≤45.
所以学校在商场最多能购买45个甲种奖品.
现学活用
9. 随着“低碳生活,绿色出行”理念的普及,新能源汽车成为大部分人
首选的交通工具.某市公交公司购买一批A、B两种型号的新能源汽车,
已知购买3辆A型汽车和1辆B型汽车共需要55万元,购买2辆A型汽车和4
辆B型汽车共需要120万元.
(1) 购买A型和B型汽车每辆各需要多少万元?
解:(1) 设购买A型汽车每辆需要x万元,B型汽车每辆需要y万元.由
题意,得解得所以购买A型汽车每辆需要
10万元,B型汽车每辆需要25万元.
(2) 若该公司计划购买A型汽车和B型汽车共15辆,且总费用不超过
220万元,则最少能购买A型汽车多少辆?
解:(2) 设购买A型汽车m辆,则购买B型汽车(15-m)辆.由题意,
得10m+25(15-m)≤220,解得m≥.因为m取正整数,所以m最小
取11.所以最少能购买A型汽车11辆.
考点六 新定义问题
典例8 对于x、y定义一种新运算M,规定:M(x,y)=mx+ny(其中
m、n均为非零常数),例如M(1,1)=m+n.已知M(1,-1)=9,
M(3,1)=7.
(1) 求m、n的值.
(2) 已知关于t的不等式组恰好有3个整数
解,求a的取值范围.
思路导引 (1) 根据条件中的新定义构建方程组即可解决问题.(2)
根据(1)中的结论和不等式组的特殊解可建立新的不等式组解决问题.
规范解答 (1) 由题意,得
解得
(2) 由题意,得
解不等式①,得t>-1.
解不等式②,得t≤a+4.
所以该不等式组的解集为-1<t≤a+4.
因为该不等式组恰好有3个整数解,
所以2≤a+4<3,即-2≤a<-1.
现学活用
10. 规定:{x}表示不小于x的最小整数,如{4}=4,{-2.6}=-2,
{-5}=-5.在此规定下任意数x都能写出如下形式:x={x}-b,
其中0≤b<1.
(1) 直接写出{x}、x、x+1的大小关系: .
(2) 根据(1)中的关系式,求满足{x+3}=5的x的取值范围.
解:(2) 因为x≤{x}<x+1,{x+3}=5,所以解得1
<x≤2.所以x的取值范围是1<x≤2.
x≤{x}<x+1
(3) 求{3.5x-2}=2x-中的x的值.
解:(3) 因为{3.5x-2}=2x-,所以由(1),得3.5x-2≤{3.5x-2}
<(3.5x-2)+1,且2x-为整数.所以3.5x-2≤2x-<(3.5x-2)
+1,解得<x≤.所以<2x-≤2.所以整数2x-的值为1或2.当2x
-=1时,得x=.当2x-=2时,得x=.所以{3.5x-2}=2x-中的x
的值为或.
考点七 学科内综合题
典例9 已知m是有理数,关于x、y的方程组的解满
足不等式2x-y<19,求m的取值范围.
思路导引 解方程组得到再根据方程组的解满足2x-y
<19,建立关于m的不等式,解不等式即可得到答案.
规范解答 记
②-①×2,得3x=6m+9,解得x=2m+3.
把x=2m+3代入①,得2m+3+y=-1,
解得y=-4-2m.
所以方程组的解为
因为关于x、y的方程组的解满足不等式2x-y<19,
所以2(2m+3)-(-4-2m)<19,解得m<.
现学活用
11. 若关于x、y的方程组的解满足x+y<2,求出满
足条件的m的所有非负整数值.
解:记①+②,得3x+3y=3m-3,即x+y=m
-1.因为x+y<2,所以m-1<2,解得m<3.所以满足条件的m的所有
非负整数值为0、1、2.
第11章 一元一次不等式
高频考点突破
考点一 不等式的基本性质
典例1 若x<y,则下列结论中,成立的是( )
A. x+2>y+2 B. -2x<-2y
C. 3x>3y D. 1-x>1-y
思路导引 直接根据不等式的基本性质逐项进行判别.
规范解答 A中,由x<y,可得x+2<y+2,原变形错误,故A不符合题
意.B中,由x<y,可得-2x>-2y,原变形错误,故B不符合题意.C
中,由x<y,可得3x<3y,原变形错误,故C不符合题意.D中,由x<
y,可得1-x>1-y,原变形正确,故D符合题意.故选D.
方法归纳
解不等式的方法
运用不等式的基本性质解决问题的关键在于熟练掌握不等式的基
本性质.特别要注意的是不等式的基本性质2中,不等式的两边都乘(或
除以)同一个负数,不等号的方向改变.
现学活用
1. 已知a>b,则下列变形中,错误的是( B )
A. a-1>b-1
B. 2a<2b
C. -2a+3<-2b+3
D. -5a<-5b
B
2. 若x+y=1,y≤2,则x的取值范围是 .
x≥-1
典例2 若x<y,且(a-3)x>(a-3)y,则a的取值范围是( )
A. a<3 B. a>3 C. a≥3 D. a≤3
思路导引 先比较所给的两个不等式,根据不等式的两边都乘a-3后,
不等号的方向变化,再利用不等式的性质确定a-3与0的大小关系,从
而解决问题.
规范解答 因为x<y,且(a-3)x>(a-3)y,所以a-3<0.所以a<
3.故选A.
现学活用
3. 已知关于x的不等式(a-1)x>1,可化为x<,试化简|1-a|
-|a-2|,正确的结果是 .
-1
考点二 不等式(组)的解集
典例3 已知a、b为常数.若ax+b>0的解集是x<,则bx-a<0的解集
是 .
思路导引 根据ax+b>0的解集是x<,可得a<0,且-=,判断b的
正负性,从而通过解不等式来解决问题.
规范解答 因为ax+b>0的解集是x<,所以a<0,-=,即a=-
3b.所以b>0.所以解不等式bx-a<0,即bx+3b<0,得x<-3.故填x<
-3.
易错警示
不能确定其中隐含条件导致错误
解答这类问题时,往往会出现不能从所给不等式的解集中挖掘字
母系数隐含的取值范围,导致解题错误,需要比较、分析不等式变形
前后不等号方向的变化,来确定字母的取值范围,进而利用隐含的字
母系数之间的数量关系求得不等式的解集.
现学活用
4. 下列不等式的解集在数轴上表示如图所示的为( D )
A. 12-6x<0 B. 12-6x≤0
C. 12-6x>0 D. 12-6x≥0
(第4题)
D
5. 不等式组的解集在数轴上表示正确的是( A )
A
考点三 解不等式(组)
典例4 (2023·湖州)解一元一次不等式组
思路导引 先解不等式组中的每一个不等式,再求它们的公共部分.
规范解答 解不等式①,得x>-1.
解不等式②,得x<2.
所以原不等式组的解集是-1<x<2.
现学活用
6. (1) 解不等式-1<,并把它的解集在数轴上表示出来.
解:该不等式的解集为x>-2.在数轴上表示不等式的解集如图所示.
(2) 解不等式组:
解:不等式组的解集为-1≤x<5.
(第6题答案)
典例5 解不等式组并写出它的正整数解.
思路导引 首先解每个不等式,两个不等式的解集的公共部分就是不等
式组的解集,然后确定解集中的正整数解即可.
规范解答 解x-3(x-2)<6,得x>0.
解x-1<,得x<4.
所以不等式组的解集是0<x<4.
所以原不等式组的正整数解是x=1、2、3.
现学活用
7. 求不等式≤-1的正整数解.
解:该不等式的解集为x≤2.所以原不等式的正整数解为x=1、2.
考点四 运用不等式组的解集解题
典例6 若关于x的不等式组无解,则a的取值范围是
( )
A. a>2 B. a≥2
C. 1<a≤2 D. 1≤a<2
思路导引 先分别表示出不等式组中两个不等式的解集,再由不等式组
的解集,确定出a的取值范围即可.
规范解答 整理不等式组,得由不等式组无解,得a≥2.故选B.
易错警示
不能逆用不等式的解集确定字母的取值范围
解答这类问题时,往往会出现确定范围不全或扩大的错误,究其
原因,是不能根据条件中不等式的解集或特殊整数解的情形,逆用不
等式的解集确定字母的取值范围.
现学活用
8. 已知整式3的值为P.
(1) 当m=5时,求P的值.
解:(1) 因为m=5,所以3=1-3m=1-3×5=-14.因为P=3,所以P=-14.
(2) 若某个关于x的不等式的解集如图所示,P为该不等式的一个解,
求m的负整数值.
解:(2) 因为P=3,所以由
题图,可得3(-m)≤5.所以m≥-.
所以m的负整数值为-1.
(第8题)
解:(3) 由题意,得解不等式②,
得x≥-3m.因为关于x的不等式组恰有两个整数解,
所以不等式组的解集为-3m≤x<1.所以不等式组的整数解是
x=0、-1.所以-2<-3m≤-1.所以≤m<.
(3) 关于x的不等式组恰有两个整数解,求m的取值范围.
考点五 运用不等式解决实际问题
典例7 学校准备为在“航天比赛”活动中获奖的学生购买奖品.已知在
商场购买3个甲种奖品和2个乙种奖品共需120元,其中甲种奖品的单价
是乙种奖品单价的2倍.
(1) 求甲、乙两种奖品的单价.
(2) 学校计划购买甲、乙两种奖品共80个,且此次购买奖品的费用不
超过1500元.正逢商场促销,所有商品一律打8折销售,则学校在商场最
多能购买多少个甲种奖品?
思路导引 (1) 设甲种奖品的单价为x元,乙种奖品的单价为y元,根
据“购买3个甲种奖品和2个乙种奖品共需120元”“甲种奖品的单价是
乙种奖品单价的2倍”,即可得出关于x、y的二元一次方程组,解之即
可.(2) 设学校在商场购买m个甲种奖品,则购买(80-m)个乙种奖
品,根据总价=单价×数量,结合此次购买奖品的费用不超过1500元,
即可得出关于m的一元一次不等式,解之取其中的最大值即可.
规范解答 (1) 设甲种奖品的单价为x元,乙种奖品的单价为y元.
由题意,得解得
所以甲种奖品的单价为30元,乙种奖品的单价为15元.
(2) 设学校在商场购买m个甲种奖品,则购买(80-m)个乙种奖品.
由题意,得30×0.8m+15×0.8(80-m)≤1500,解得m≤45.
所以学校在商场最多能购买45个甲种奖品.
现学活用
9. 随着“低碳生活,绿色出行”理念的普及,新能源汽车成为大部分人
首选的交通工具.某市公交公司购买一批A、B两种型号的新能源汽车,
已知购买3辆A型汽车和1辆B型汽车共需要55万元,购买2辆A型汽车和4
辆B型汽车共需要120万元.
(1) 购买A型和B型汽车每辆各需要多少万元?
解:(1) 设购买A型汽车每辆需要x万元,B型汽车每辆需要y万元.由
题意,得解得所以购买A型汽车每辆需要
10万元,B型汽车每辆需要25万元.
(2) 若该公司计划购买A型汽车和B型汽车共15辆,且总费用不超过
220万元,则最少能购买A型汽车多少辆?
解:(2) 设购买A型汽车m辆,则购买B型汽车(15-m)辆.由题意,
得10m+25(15-m)≤220,解得m≥.因为m取正整数,所以m最小
取11.所以最少能购买A型汽车11辆.
考点六 新定义问题
典例8 对于x、y定义一种新运算M,规定:M(x,y)=mx+ny(其中
m、n均为非零常数),例如M(1,1)=m+n.已知M(1,-1)=9,
M(3,1)=7.
(1) 求m、n的值.
(2) 已知关于t的不等式组恰好有3个整数
解,求a的取值范围.
思路导引 (1) 根据条件中的新定义构建方程组即可解决问题.(2)
根据(1)中的结论和不等式组的特殊解可建立新的不等式组解决问题.
规范解答 (1) 由题意,得
解得
(2) 由题意,得
解不等式①,得t>-1.
解不等式②,得t≤a+4.
所以该不等式组的解集为-1<t≤a+4.
因为该不等式组恰好有3个整数解,
所以2≤a+4<3,即-2≤a<-1.
现学活用
10. 规定:{x}表示不小于x的最小整数,如{4}=4,{-2.6}=-2,
{-5}=-5.在此规定下任意数x都能写出如下形式:x={x}-b,
其中0≤b<1.
(1) 直接写出{x}、x、x+1的大小关系: .
(2) 根据(1)中的关系式,求满足{x+3}=5的x的取值范围.
解:(2) 因为x≤{x}<x+1,{x+3}=5,所以解得1
<x≤2.所以x的取值范围是1<x≤2.
x≤{x}<x+1
(3) 求{3.5x-2}=2x-中的x的值.
解:(3) 因为{3.5x-2}=2x-,所以由(1),得3.5x-2≤{3.5x-2}
<(3.5x-2)+1,且2x-为整数.所以3.5x-2≤2x-<(3.5x-2)
+1,解得<x≤.所以<2x-≤2.所以整数2x-的值为1或2.当2x
-=1时,得x=.当2x-=2时,得x=.所以{3.5x-2}=2x-中的x
的值为或.
考点七 学科内综合题
典例9 已知m是有理数,关于x、y的方程组的解满
足不等式2x-y<19,求m的取值范围.
思路导引 解方程组得到再根据方程组的解满足2x-y
<19,建立关于m的不等式,解不等式即可得到答案.
规范解答 记
②-①×2,得3x=6m+9,解得x=2m+3.
把x=2m+3代入①,得2m+3+y=-1,
解得y=-4-2m.
所以方程组的解为
因为关于x、y的方程组的解满足不等式2x-y<19,
所以2(2m+3)-(-4-2m)<19,解得m<.
现学活用
11. 若关于x、y的方程组的解满足x+y<2,求出满
足条件的m的所有非负整数值.
解:记①+②,得3x+3y=3m-3,即x+y=m
-1.因为x+y<2,所以m-1<2,解得m<3.所以满足条件的m的所有
非负整数值为0、1、2.
同课章节目录
