2024年中考数学苏科版二轮复习高频考点突破课件第8章 幂的运算(32张ppt)
文档属性
| 名称 | 2024年中考数学苏科版二轮复习高频考点突破课件第8章 幂的运算(32张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 366.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 00:00:00 | ||
图片预览







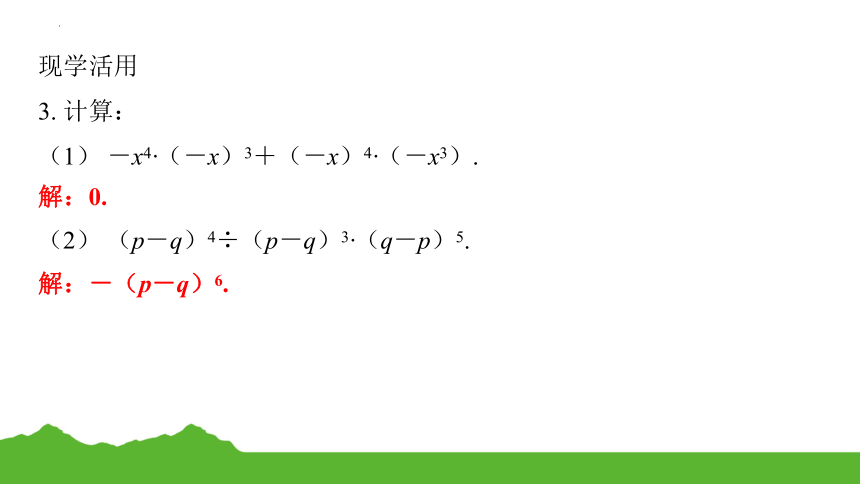




文档简介
(共32张PPT)
第8章 幂的运算
高频考点突破
考点一 同底数幂的乘法与除法
典例1 下列计算正确的是( )
A. a3+a4=a7 B. a3·a4=a7
C. a4÷a3=a7 D. (a3)4=a7
思路导引 分别根据合并同类项的法则、同底数幂的乘除法法则、幂的
乘方法则对各选项进行逐一判断即可.
规范解答 A选项中,a3与a4不是同类项,不能合并,则原计算错误,
不符合题意.B选项中,a3·a4=a7,正确,符合题意.C选项中,a4÷a3=
a,则原计算错误,不符合题意.D选项中,(a3)4=a12,则原计算错
误,不符合题意.故选B.
易错警示
混淆法则,不能正确运用导致错误
运用同底数幂的乘法与除法法则进行运算时,常常会因为不能正
确理解法则,而出现相互混淆的现象.因此,需要理解法则的内涵,切
不可死记硬背.
现学活用
1. 下列计算结果为a8的是( C )
A. a2+a6 B. a2·a4
C. (a4)2 D. a16÷a2
2. (2023·朝阳)下列运算正确的是( B )
A. 5a2-4a2=1 B. a7÷a4=a3
C. (a3)2=a5 D. a2·a3=a6
C
B
典例2 计算:y3·y2-(-y4)·y-y9÷y4.
思路导引 先算同底数幂的乘法及同底数幂的除法,再合并同类项
即可.
规范解答 原式=y5-(-y5)-y5=y5+y5-y5=y5.
现学活用
3. 计算:
(1) -x4·(-x)3+(-x)4·(-x3).
解:0.
(2) (p-q)4÷(p-q)3·(q-p)5.
解:-(p-q)6.
考点二 幂的乘方、积的乘方
典例3 (2023·山西)下列计算正确的是( )
A. a2·a3=a6 B. (-a3b)2=-a6b2
C. a6÷a3=a2 D. (a2)3=a6
思路导引 分别根据同底数幂的乘除法法则、幂的乘方与积的乘方法则
对各选项进行逐一判断即可.
规范解答 A选项中,a2·a3=a5,则原计算错误,不符合题意.B选项
中,(-a3b)2=a6b2,则原计算错误,不符合题意.C选项中,a6÷a3=
a3,则原计算错误,不符合题意.D选项中,(a2)3=a6,正确,符合题
意.故选D.
现学活用
4. (2023·株洲)计算(3a)2的结果为( D )
A. 5a B. 3a2 C. 6a2 D. 9a2
5. (2023·安徽)下列计算正确的是( C )
A. a4+a4=a8 B. a4·a4=a16
C. (a4)4=a16 D. a8÷a4=a2
D
C
典例4 (2023·乐山)若m、n满足3m-n-4=0,则8m÷2n= .
思路导引 直接利用幂的乘方运算法则将原式变形,进而计算得出
答案.
规范解答 因为3m-n-4=0,所以3m-n=4.所以8m÷2n=23m÷2n=
23m-n=24=16.故填16.
现学活用
6. 若a=23,b=32,则1818= (用含a、b的代数式表示).
7. 已知2×8n×16n=222,则n的值为 .
a6b18
3
考点三 运用零指数幂、负整数指数幂的意义运算
典例5 (2023·杭州模拟)计算:
|-8|-(π+3)0++(-1)2022.
思路导引 直接利用绝对值的性质、零指数幂的性质、负整数指数幂的
性质、有理数的乘方运算法则进行化简,得出答案.
规范解答 原式=8-1-4+1=4.
现学活用
8. 计算:(-2)3÷4+-|-2|+(3-π)0.
解:原式=-8÷4+4-2+1=-2+4-2+1=1.
考点四 较小数的科学记数法
典例6 (2023·遂宁)纳米是表示微小距离的单位,1纳米=0.000001毫
米,而1毫米相当于我们通常使用的刻度尺上的一小格.某研究员领导的
研究小组研制出世界上最细的碳纳米管,它的直径约为0.5纳米.0.5纳米
相当于0.0000005毫米,数据0.0000005用科学记数法可以表示为( )
A. 0.5×10-6 B. 0.5×10-7
C. 5×10-6 D. 5×10-7
思路导引 直接用科学记数法表示即可.
规范解答 0.0000005=5×10-7.故选D.
方法归纳
利用科学记数法表示绝对值小于1的数的方法
绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n,
与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原
数左边起第一个不为零的数字前面的0的个数所决定.
现学活用
9. (2023·日照)芯片内部有数以亿计的晶体管,人们追求更高质量的
芯片和更低的电力功耗,需要设计体积更小的晶体管.目前,某品牌手
机自主研发了最新型号的芯片,其晶体管栅极的宽度约为0.000000014
米,将数据0.000000014用科学记数法表示为( A )
A. 1.4×10-8 B. 14×10-7
C. 0.14×10-6 D. 1.4×10-9
A
考点五 幂的有关运算
典例7 计算:
(1) (2x3)2+(-2x2)3.
(2) (-3a4)2-a2·a3·a4-a10÷a2.
思路导引 (1) 先利用积的乘方计算,再合并同类项.(2) 先利用积
的乘方、同底数幂的乘法、同底数幂的除法计算,再合并同类项.
规范解答 (1) 原式=4x6-8x6=-4x6.
(2) 原式=9a8-a9-a8=8a8-a9.
易错警示
不能正确确定运算顺序导致解题错误
这类问题主要考查同底数幂的除法、同底数幂的乘法、积的乘
方,解答的关键是掌握相应的运算法则.解答时,与有理数的运算顺序
类似,先算乘方,再算乘除,最后算加减,有括号的先算括号里面.
现学活用
10. 计算:
(1) x5·x7+x6·(-x3)2+2(x3)4.
解:原式=x12+x6·x6+2x12=x12+x12+2x12=4x12.
(2) (-a3)5-a6·a5·a4-2a17÷a2.
解:原式=-a15-a15-2a15=-4a15.
典例8 已知n是正整数,且x4n=2,求(2x2n)4-(x3)4n的值.
思路导引 先利用积的乘方及幂的乘方计算,再逆用幂的乘方将其化成
含有x4n的形式,最后把x4n=2代入计算即可.
规范解答 原式=16x8n-x12n=16(x4n)2-(x4n)3.
当x4n=2时,原式=16×22-23=56.
现学活用
11. 已知n是正整数,且x3n=2,求(3x3n)2+(-2x2n)3的值.
解:原式=9x6n-8x6n=x6n=(x3n)2.当x3n=2时,原式=22=4.
考点六 幂的运算性质的逆用
典例9 已知10a=2,10b=3,求:
(1) 102a+103b的值.
(2) 102a+3b的值.
思路导引 逆用幂的运算性质进行解题.(1) 把原式化为(10a)2+
(10b)3进行计算即可.(2) 把原式化为102a×103b进行计算即可.
规范解答 (1) 因为10a=2,10b=3,
所以原式=(10a)2+(10b)3=22+33=4+27=31.
(2) 因为10a=2,10b=3,
所以原式=102a×103b=(10a)2×(10b)3=22×33=4×27=108.
现学活用
12. 已知am=2,an=3,求:
(1) a4m+3n的值.
解:(1) 因为am=2,an=3,所以a4m+3n=a4m·a3n=(am)4·(an)3=
24×33=16×27=432.
(2) a5m-2n的值.
解:(2) 因为am=2,an=3,所以a5m-2n=a5m÷a2n=(am)5÷(an)2
=25÷32=.
典例10 已知a=334,b=251,c=425,则a、b、c的大小关系
为 (用“<”连接).
思路导引 根据幂的乘方,先把a、b、c变形,再进行比较.
规范解答 a=334=(32)17=917;b=251=(23)17=817;c=425=250.
因为817<917,250<251,所以c<b<a.故填c<b<a.
现学活用
13. (1) 3108与2144的大小关系用“>”连接是 .
(2) 若a=,b=,则a b(填“>”“<”或“=”).
3108>2144
=
考点七 阅读理解题
典例11 规定:若两数a、b满足am=b,则记为(a,b)=m.例如,因
为23=8,所以记为(2,8)=3.我们还可以利用该规定来说明等式
(3,3)+(3,5)=(3,15)成立.理由:设(3,3)=m,(3,
5)=n,则3m=3,3n=5,故3m×3n=3m+n=3×5=15,则(3,15)=
m+n,即(3,3)+(3,5)=(3,15).
(1) 填空:(6,36)= .
(2) 计算:(7,3)+(7,10)= .
(3) 如果(3,m+17)=4,(9,m)=n,那么(3, )=2n.
(4) 若(3n,2n)=s,(3,2)=t,请说明s与t之间的关系(n为正
整数).
思路导引 (1) 令(6,36)=m.根据所给的规定,可得6m=36,即可
求出m的值.(2) 令(7,3)=m,(7,10)=n.根据所给的规定,可
得7m×7n=7m+n=30,即可计算(7,3)+(7,10)的结果.(3) 由
题意,可得34=m+17,解得m=64,再由9n=32n=64,即可求解.(4)
由题意,可得3ns=2n,3t=2,则3ns=3tn,从而得到s=t.
规范解答 (1) 令(6,36)=m.所以6m=36.所以m=2.故填2.
(2) 令(7,3)=m,(7,10)=n.所以7m=3,7n=10.所以7m×7n=
7m+n=30.所以(7,3)+(7,10)=m+n.所以(7,3)+(7,10)
=30.故填30.
(3) 因为(3,m+17)=4,所以34=m+17,解得m=64.因为(9,
m)=n,所以9n=m.所以9n=32n=64.故填64.
(4) 因为(3n,2n)=s,(3,2)=t,
所以3ns=2n,3t=2.所以3tn=2n.
所以3ns=3tn.所以s=t.
现学活用
14. 规定两数a、b之间的一种运算,记作(a,b):如果ac=b,那么
(a,b)=c.例如,因为23=8,所以(2,8)=3.
(1) 填空:(5,25)= ,(5,1)= ,= .
(2) 小明在研究这种运算时发现一个特征:(3n,4n)=(3,4).小
明给出了如下的说明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=
4n,所以3x=4,即(3,4)=x.所以(3n,4n)=(3,4).
2
0
-2
试解答下列问题:
① 计算:(8,1000)-(32,100000).
② 请你尝试运用这种方法说明下面这个等式:(3,20)-(3,4)=
(3,5).
解:① (8,1000)-(32,100000)=(23,103)-(25,105)=
(2,10)-(2,10)=0.
② 设3x=4,3y=5,则3x×3y=3x+y=4×5=20.所以(3,4)=x,
(3,5)=y,(3,20)=x+y.所以(3,20)-(3,4)=x+y-x=
y=(3,5),即(3,20)-(3,4)=(3,5).
第8章 幂的运算
高频考点突破
考点一 同底数幂的乘法与除法
典例1 下列计算正确的是( )
A. a3+a4=a7 B. a3·a4=a7
C. a4÷a3=a7 D. (a3)4=a7
思路导引 分别根据合并同类项的法则、同底数幂的乘除法法则、幂的
乘方法则对各选项进行逐一判断即可.
规范解答 A选项中,a3与a4不是同类项,不能合并,则原计算错误,
不符合题意.B选项中,a3·a4=a7,正确,符合题意.C选项中,a4÷a3=
a,则原计算错误,不符合题意.D选项中,(a3)4=a12,则原计算错
误,不符合题意.故选B.
易错警示
混淆法则,不能正确运用导致错误
运用同底数幂的乘法与除法法则进行运算时,常常会因为不能正
确理解法则,而出现相互混淆的现象.因此,需要理解法则的内涵,切
不可死记硬背.
现学活用
1. 下列计算结果为a8的是( C )
A. a2+a6 B. a2·a4
C. (a4)2 D. a16÷a2
2. (2023·朝阳)下列运算正确的是( B )
A. 5a2-4a2=1 B. a7÷a4=a3
C. (a3)2=a5 D. a2·a3=a6
C
B
典例2 计算:y3·y2-(-y4)·y-y9÷y4.
思路导引 先算同底数幂的乘法及同底数幂的除法,再合并同类项
即可.
规范解答 原式=y5-(-y5)-y5=y5+y5-y5=y5.
现学活用
3. 计算:
(1) -x4·(-x)3+(-x)4·(-x3).
解:0.
(2) (p-q)4÷(p-q)3·(q-p)5.
解:-(p-q)6.
考点二 幂的乘方、积的乘方
典例3 (2023·山西)下列计算正确的是( )
A. a2·a3=a6 B. (-a3b)2=-a6b2
C. a6÷a3=a2 D. (a2)3=a6
思路导引 分别根据同底数幂的乘除法法则、幂的乘方与积的乘方法则
对各选项进行逐一判断即可.
规范解答 A选项中,a2·a3=a5,则原计算错误,不符合题意.B选项
中,(-a3b)2=a6b2,则原计算错误,不符合题意.C选项中,a6÷a3=
a3,则原计算错误,不符合题意.D选项中,(a2)3=a6,正确,符合题
意.故选D.
现学活用
4. (2023·株洲)计算(3a)2的结果为( D )
A. 5a B. 3a2 C. 6a2 D. 9a2
5. (2023·安徽)下列计算正确的是( C )
A. a4+a4=a8 B. a4·a4=a16
C. (a4)4=a16 D. a8÷a4=a2
D
C
典例4 (2023·乐山)若m、n满足3m-n-4=0,则8m÷2n= .
思路导引 直接利用幂的乘方运算法则将原式变形,进而计算得出
答案.
规范解答 因为3m-n-4=0,所以3m-n=4.所以8m÷2n=23m÷2n=
23m-n=24=16.故填16.
现学活用
6. 若a=23,b=32,则1818= (用含a、b的代数式表示).
7. 已知2×8n×16n=222,则n的值为 .
a6b18
3
考点三 运用零指数幂、负整数指数幂的意义运算
典例5 (2023·杭州模拟)计算:
|-8|-(π+3)0++(-1)2022.
思路导引 直接利用绝对值的性质、零指数幂的性质、负整数指数幂的
性质、有理数的乘方运算法则进行化简,得出答案.
规范解答 原式=8-1-4+1=4.
现学活用
8. 计算:(-2)3÷4+-|-2|+(3-π)0.
解:原式=-8÷4+4-2+1=-2+4-2+1=1.
考点四 较小数的科学记数法
典例6 (2023·遂宁)纳米是表示微小距离的单位,1纳米=0.000001毫
米,而1毫米相当于我们通常使用的刻度尺上的一小格.某研究员领导的
研究小组研制出世界上最细的碳纳米管,它的直径约为0.5纳米.0.5纳米
相当于0.0000005毫米,数据0.0000005用科学记数法可以表示为( )
A. 0.5×10-6 B. 0.5×10-7
C. 5×10-6 D. 5×10-7
思路导引 直接用科学记数法表示即可.
规范解答 0.0000005=5×10-7.故选D.
方法归纳
利用科学记数法表示绝对值小于1的数的方法
绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n,
与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原
数左边起第一个不为零的数字前面的0的个数所决定.
现学活用
9. (2023·日照)芯片内部有数以亿计的晶体管,人们追求更高质量的
芯片和更低的电力功耗,需要设计体积更小的晶体管.目前,某品牌手
机自主研发了最新型号的芯片,其晶体管栅极的宽度约为0.000000014
米,将数据0.000000014用科学记数法表示为( A )
A. 1.4×10-8 B. 14×10-7
C. 0.14×10-6 D. 1.4×10-9
A
考点五 幂的有关运算
典例7 计算:
(1) (2x3)2+(-2x2)3.
(2) (-3a4)2-a2·a3·a4-a10÷a2.
思路导引 (1) 先利用积的乘方计算,再合并同类项.(2) 先利用积
的乘方、同底数幂的乘法、同底数幂的除法计算,再合并同类项.
规范解答 (1) 原式=4x6-8x6=-4x6.
(2) 原式=9a8-a9-a8=8a8-a9.
易错警示
不能正确确定运算顺序导致解题错误
这类问题主要考查同底数幂的除法、同底数幂的乘法、积的乘
方,解答的关键是掌握相应的运算法则.解答时,与有理数的运算顺序
类似,先算乘方,再算乘除,最后算加减,有括号的先算括号里面.
现学活用
10. 计算:
(1) x5·x7+x6·(-x3)2+2(x3)4.
解:原式=x12+x6·x6+2x12=x12+x12+2x12=4x12.
(2) (-a3)5-a6·a5·a4-2a17÷a2.
解:原式=-a15-a15-2a15=-4a15.
典例8 已知n是正整数,且x4n=2,求(2x2n)4-(x3)4n的值.
思路导引 先利用积的乘方及幂的乘方计算,再逆用幂的乘方将其化成
含有x4n的形式,最后把x4n=2代入计算即可.
规范解答 原式=16x8n-x12n=16(x4n)2-(x4n)3.
当x4n=2时,原式=16×22-23=56.
现学活用
11. 已知n是正整数,且x3n=2,求(3x3n)2+(-2x2n)3的值.
解:原式=9x6n-8x6n=x6n=(x3n)2.当x3n=2时,原式=22=4.
考点六 幂的运算性质的逆用
典例9 已知10a=2,10b=3,求:
(1) 102a+103b的值.
(2) 102a+3b的值.
思路导引 逆用幂的运算性质进行解题.(1) 把原式化为(10a)2+
(10b)3进行计算即可.(2) 把原式化为102a×103b进行计算即可.
规范解答 (1) 因为10a=2,10b=3,
所以原式=(10a)2+(10b)3=22+33=4+27=31.
(2) 因为10a=2,10b=3,
所以原式=102a×103b=(10a)2×(10b)3=22×33=4×27=108.
现学活用
12. 已知am=2,an=3,求:
(1) a4m+3n的值.
解:(1) 因为am=2,an=3,所以a4m+3n=a4m·a3n=(am)4·(an)3=
24×33=16×27=432.
(2) a5m-2n的值.
解:(2) 因为am=2,an=3,所以a5m-2n=a5m÷a2n=(am)5÷(an)2
=25÷32=.
典例10 已知a=334,b=251,c=425,则a、b、c的大小关系
为 (用“<”连接).
思路导引 根据幂的乘方,先把a、b、c变形,再进行比较.
规范解答 a=334=(32)17=917;b=251=(23)17=817;c=425=250.
因为817<917,250<251,所以c<b<a.故填c<b<a.
现学活用
13. (1) 3108与2144的大小关系用“>”连接是 .
(2) 若a=,b=,则a b(填“>”“<”或“=”).
3108>2144
=
考点七 阅读理解题
典例11 规定:若两数a、b满足am=b,则记为(a,b)=m.例如,因
为23=8,所以记为(2,8)=3.我们还可以利用该规定来说明等式
(3,3)+(3,5)=(3,15)成立.理由:设(3,3)=m,(3,
5)=n,则3m=3,3n=5,故3m×3n=3m+n=3×5=15,则(3,15)=
m+n,即(3,3)+(3,5)=(3,15).
(1) 填空:(6,36)= .
(2) 计算:(7,3)+(7,10)= .
(3) 如果(3,m+17)=4,(9,m)=n,那么(3, )=2n.
(4) 若(3n,2n)=s,(3,2)=t,请说明s与t之间的关系(n为正
整数).
思路导引 (1) 令(6,36)=m.根据所给的规定,可得6m=36,即可
求出m的值.(2) 令(7,3)=m,(7,10)=n.根据所给的规定,可
得7m×7n=7m+n=30,即可计算(7,3)+(7,10)的结果.(3) 由
题意,可得34=m+17,解得m=64,再由9n=32n=64,即可求解.(4)
由题意,可得3ns=2n,3t=2,则3ns=3tn,从而得到s=t.
规范解答 (1) 令(6,36)=m.所以6m=36.所以m=2.故填2.
(2) 令(7,3)=m,(7,10)=n.所以7m=3,7n=10.所以7m×7n=
7m+n=30.所以(7,3)+(7,10)=m+n.所以(7,3)+(7,10)
=30.故填30.
(3) 因为(3,m+17)=4,所以34=m+17,解得m=64.因为(9,
m)=n,所以9n=m.所以9n=32n=64.故填64.
(4) 因为(3n,2n)=s,(3,2)=t,
所以3ns=2n,3t=2.所以3tn=2n.
所以3ns=3tn.所以s=t.
现学活用
14. 规定两数a、b之间的一种运算,记作(a,b):如果ac=b,那么
(a,b)=c.例如,因为23=8,所以(2,8)=3.
(1) 填空:(5,25)= ,(5,1)= ,= .
(2) 小明在研究这种运算时发现一个特征:(3n,4n)=(3,4).小
明给出了如下的说明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=
4n,所以3x=4,即(3,4)=x.所以(3n,4n)=(3,4).
2
0
-2
试解答下列问题:
① 计算:(8,1000)-(32,100000).
② 请你尝试运用这种方法说明下面这个等式:(3,20)-(3,4)=
(3,5).
解:① (8,1000)-(32,100000)=(23,103)-(25,105)=
(2,10)-(2,10)=0.
② 设3x=4,3y=5,则3x×3y=3x+y=4×5=20.所以(3,4)=x,
(3,5)=y,(3,20)=x+y.所以(3,20)-(3,4)=x+y-x=
y=(3,5),即(3,20)-(3,4)=(3,5).
同课章节目录
