2024年中考数学苏科版二轮复习高频考点突破课件第9章 整式乘法与因式分解(40张ppt)
文档属性
| 名称 | 2024年中考数学苏科版二轮复习高频考点突破课件第9章 整式乘法与因式分解(40张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 586.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 11:14:14 | ||
图片预览










文档简介
(共40张PPT)
第9章 整式乘法与因式分解
高频考点突破
考点一 单项式与单项式、多项式相乘
典例1 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=
-2.
思路导引 首先根据单项式与多项式相乘的法则去掉括号,然后合并同
类项,最后代入已知的数值计算求值.
规范解答 原式=6a3-12a2+9a-6a3-8a2=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-20×4-9×2=
-98.
现学活用
1. 已知x2-2=y,则x(x-2023y)-y(1-2023x)的值为( A )
A. 2 B. 0 C. -2 D. 1
2. 下列计算中,正确的是( D )
A. 3ab+2b=5ab
B. (-x2)·(-x)2=x4
C. (-2ab2)3=8a3b6
D. 2m(n2-3m2)=2mn2-6m3
A
D
考点二 多项式乘多项式
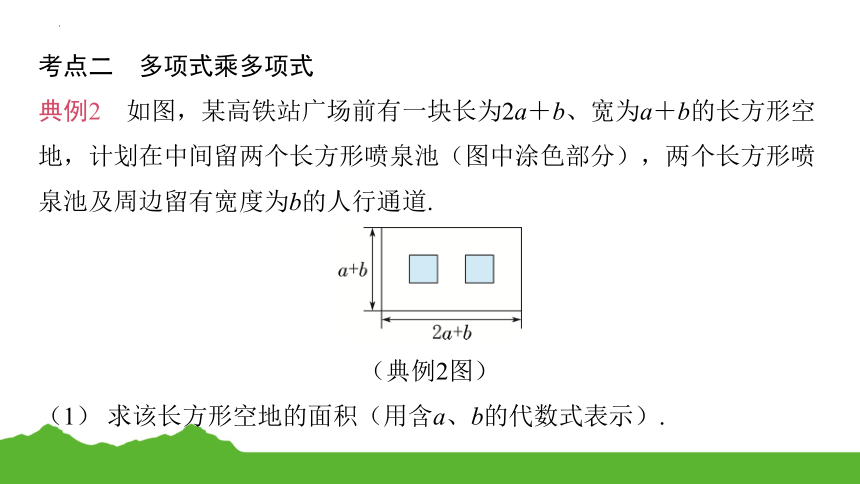
典例2 如图,某高铁站广场前有一块长为2a+b、宽为a+b的长方形空
地,计划在中间留两个长方形喷泉池(图中涂色部分),两个长方形喷
泉池及周边留有宽度为b的人行通道.
(典例2图)
(1) 求该长方形空地的面积(用含a、b的代数式表示).
(2) 求这两个长方形喷泉池的总面积(用含a、b的代数式表示).
(3) 当a=200,b=100时,求这两个长方形喷泉池的总面积.
思路导引 (1) 根据长方形的面积公式列式并计算求得.(2) 根据
“长为2a+b、宽为a+b的长方形空地”“两个长方形喷泉池及周边留
有宽度为b的人行通道”,进行列式计算.(3) 把a=200,b=100代入
(2)中得到的结果进行计算,即可求得结果.
规范解答 (1) 由题意,得(a+b)(2a+b)=2a2+3ab+b2.
所以该长方形空地的面积为2a2+3ab+b2.
(2) 由题意,得(a+b-2b)(2a+b-3b)=(a-b)(2a-2b)
=2a2-4ab+2b2.
所以这两个长方形喷泉池的总面积为2a2-4ab+2b2.
(3) 当a=200,b=100时,2a2-4ab+2b2=2×2002-4×200×100+
2×1002=20000.
所以这两个长方形喷泉池的总面积为20000.
现学活用
3. 已知a+b=11,ab=1,求(a-2)(b-2)的值.
解:(a-2)(b-2)=ab-2a-2b+4=ab-2(a+b)+4.因为a+b
=11,ab=1,所以原式=1-2×11+4=1-22+4=-17.
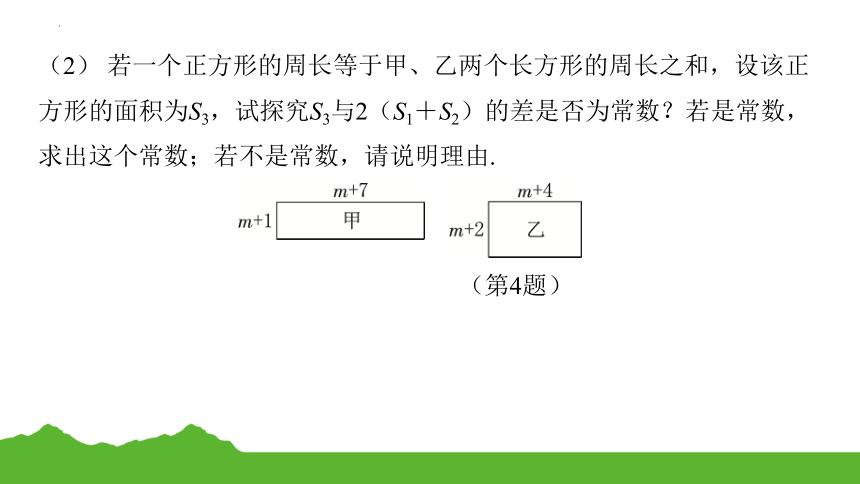
4. 甲、乙两个长方形的长、宽如图所示(m为正整数),其面积分别为
S1、S2.
(1) 请用含m的代数式分别表示S1、S2.
解:(1) S1=(m+7)(m+1)=m2+8m+7;S2=(m+4)(m+
2)=m2+6m+8.
(2) 若一个正方形的周长等于甲、乙两个长方形的周长之和,设该正
方形的面积为S3,试探究S3与2(S1+S2)的差是否为常数?若是常数,
求出这个常数;若不是常数,请说明理由.
(第4题)
解:(2) 是常数.设该正方形的边长为a.根据题意,得4a=2(m+7+
m+1)+2(m+4+m+2),解得a=2m+7.所以S3=(2m+7)2.所以
S3-2(S1+S2)=(2m+7)2-2(m2+8m+7+m2+6m+8)=4m2
+28m+49-4m2-28m-30=19.所以S3 与 2(S1+S2)的差是常数19.
考点三 乘法公式
典例3 (2023·盐城)先化简,再求值:(a+3b)2+(a+3b)(a-
3b),其中a=2,b=-1.
思路导引 依据题意,利用完全平方公式和平方差公式将原式进行化
简,再将a、b的值代入计算即可.
规范解答 原式=a2+6ab+9b2+a2-9b2=2a2+6ab.
当a=2,b=-1时,原式=2×22+6×2×(-1)=8-12=-4.
现学活用
5. 先化简,再求值:4(x+1)2-4(x-1)·(x+1)+(1-x)2,其
中x=-2.
解:原式=4(x+1)2+4(1-x)(x+1)+(1-x)2=[2(x+1)
+1-x]2=(x+3)2=x2+6x+9.把x=-2代入,得原式=(-2)2+
6×(-2)+9=4-12+9=1.
典例4 通常,用两种不同的方法计算同一个图形的面积可以得到一个
恒等式.如图,将一个边长为a+b的正方形分割成四个部分(两个正方
形和两个长方形),请观察图形,解答下列问题:
(1) 根据图中条件,用两种方法表示该图形的总面积,可得如下
公式: .
(2) 如果图中的a、b(a>b>0)满足a2+b2=70,
ab=15,求a+b的值.
(典例4图)
(3) 已知(x+9)2+(x-1)2=124,求(x+9)(x-1)的值.
(典例4图)
思路导引 (1) 根据该图形的总面积为(a+b)2或a2+2ab+b2可得
结果.(2) 由(1)中的结果,可得(a+b)2=a2+2ab+b2,根据a2+
b2=70,ab=15,可求得(a+b)2的值,即可求a+b的值.(3) 设x+9
=a,x-1=b,则可求得a-b的值,根据(a-b)2=a2+b2-2ab代入
计算可求得ab=12,即可求得(x+9)(x-1)的值.
规范解答 (1) 该图形的总面积为(a+b)2或a2+2ab+b2.故填(a+
b)2=a2+2ab+b2.
(2) 由(1)中的结果,可得(a+b)2=a2+2ab+b2,
所以当a2+b2=70,ab=15时,(a+b)2=70+2×15=100.
又因为a>b>0,所以a+b=10.
(3) 设x+9=a,x-1=b,则(x+9)2+(x-1)2=a2+b2=124.
所以a-b=(x+9)-(x-1)=10.
因为(a-b)2=a2+b2-2ab,a-b=10,a2+b2=124,所以100=124
-2ab.
所以ab=12.
所以(x+9)(x-1)=ab=12.
现学活用
6. 如图①所示为一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其
平均分成四个小长方形,然后用这四个小长方形拼成的一个“回”形正
方形(如图②).
(1) 观察图②,可以得到(a+b)2-(a-b)2= .
4ab
(2) 当(x-8)(15-x)=6时,求(2x-23)2的值.
(第6题)
解:设x-8=a,15-x=b,则ab=(x-8)(15-x)=6.所以a+b=
x-8+15-x=7,a-b=2x-23.因为(a+b)2-(a-b)2=4ab,所
以(a-b)2=(a+b)2-4ab=72-4×6=25,即(2x-23)2=25.
考点四 因式分解
典例5 将9(a-b)2+12(a2-b2)+4(a+b)2分解因式的结果是
( )
A. (5a-b)2
B. (5a+b)2
C. (5a-2b)2
D. (3a-2b)(3a+2b)
思路导引 把9(a-b)2、4(a+b)2分别看成是[3(a-b)]2、[2(a
+b)]2,把12(a2-b2)看成是3(a-b)与2(a+b)的积的2倍,再
直接利用完全平方公式分解因式得出结果.
规范解答 原式=[3(a-b)+2(a+b)]2=(5a-b)2.故选A.
现学活用
7. 多项式m2-4与m2-4m+4有相同的因式为( B )
A. m+2 B. m-2 C. m+4 D. m-4
B
典例6 分解因式:
(1) 3a2-6ab+3b2.
(2) x2(m-2)+y2(2-m).
思路导引 (1) 先提公因式,再利用完全平方公式继续分解即可.
(2) 先提公因式,再利用平方差公式继续分解即可.
规范解答 (1) 原式=3(a2-2ab+b2)=3(a-b)2.
(2) 原式=(m-2)(x2-y2)=(m-2)(x+y)(x-y).
方法归纳
分解因式的一般步骤
1. 如果多项式的首项为负,应先提取负号;2. 如果多项式的各项
含有公因式,那么先提取公因式,再进一步分解因式;3. 如果各项没
有公因式,那么可观察该多项式是否具有完全平方或平方差公式的特
征,尝试运用公式法来分解;4. 如果用上述方法不能分解,再尝试用
分组法、拆项法、补项法、十字交叉法来分解;5. 注意检验分解因式
的最终结果(不能再继续分解).
现学活用
8. 分解因式:
(1) 3b(a-b)+a2-ab.
解:原式=3b(a-b)+a(a-b)=(a-b)(3b+a).
(2) (x2+1)2-4x2.
解:原式=(x2+1+2x)(x2+1-2x)=(x+1)2(x-1)2.
9. 若一个三角形的三边长分别为a、b、c,且满足a2+2b2+c2-2ab-
2bc=0.试判断该三角形的形状,并说明理由.
解:该三角形是等边三角形.
理由:因为a2+2b2+c2-2ab-2bc=0,所以a2-2ab+b2+b2-2bc+c2
=0.所以(a-b)2+(b-c)2=0.所以a-b=0且b-c=0.所以a=b且b
=c,即a=b=c.所以该三角形是等边三角形.
典例7 若a2(b+c)=b2(a+c)=2023,a≠b,则abc的值为( )
A. 2023 B. 1011
C. -2023 D. 2024
思路导引 将已知等式利用提公因式法进行整体变形,进而探求abc
的值.
规范解答 因为a2(b+c)=b2(a+c)=2023,所以a2(b+c)-b2
(a+c)=0,即a2b+a2c-ab2-b2c=0.整理,得ab(a-b)+c(a+
b)(a-b)=0.所以(a-b)(ab+ac+bc)=0.因为a≠b,所以a-
b≠0.所以ab+ac+bc=0,即ab+bc=-ac.因为b2(a+c)=b(ab+
bc)=2023,所以b·(-ac)=2023.所以abc=-2023.故选C.
现学活用
10. 已知x-y=2,y-z=-1,求x2+y2+z2-xy-yz-xz的值.
解:因为x-y=2,y-z=-1,所以x-z=(x-y)+(y-z)=1.所
以x2+y2+z2-xy-yz-xz=(2x2+2y2+2z2-2xy-2yz-2xz)=[(x
-y)2+(y-z)2+(x-z)2]=×[22+(-1)2+12]=×6=3.
考点五 代数推理题
典例8 小敏和小华对一些四位数(a、b、c、d均为不超过9的正整
数)进行了观察、猜想,请你帮助他们一起完成探究.
(1) 这个四位数可用含a、b、c、d的代数式表示为
.
(2) 小敏尝试将一些四位数倒排后,再与原数相加,发现和都为11的
倍数.如1234+4321=5555=505×11,4258+8524=12782=1162×11.
请仿照小敏的做法再举一个具体的例子: .你认
为上述结论对于一般的+也成立吗?请说明理由.
(3) 小华认为如果一个四位数的四个数字之和是9的倍数,那么这个
四位数也是9的倍数.如3231=359×9,4455=495×9,6948=772×9.请
仿照小华的做法再举一个具体的例子: .你认为
上述结论对于一般的(a+b+c+d=9k,k是正整数)也成立吗?
请说明理由.
思路导引 (1) 用多位数的表示方法直接表示即可.(2) 用多位数的
表示方法表示出这两个四位数相加,合并同类项,提取公因式即可.
(3) 用多位数的表示方法表示出四位数,然后用拆项法,拆出四位数
的各位数字之和,整理可得结论成立.
规范解答 (1) 1000a+100b+10c+d.
(2) 答案不唯一,如2345+5432=7777=707×11.
成立.
理由:因为+=(1000a+100b+10c+d)+(1000d+100c+
10b+a)=1001a+110b+110c+1001d=11(91a+91d+10b+10c),
91a+91d+10b+10c是整数,
所以+的结果为11的倍数.
(3) 答案不唯一,如8181=909×9.
成立.
理由:因为=1000a+100b+10c+d=(999a+99b+9c)+(a+b
+c+d)=9(111a+11b+c)+9k=9(111a+11b+c+k),111a+
11b+c+k是整数,
所以为9的倍数.
现学活用
11. 发现:任意三个连续偶数的平方和是4的倍数.
(1) (-2)2+02+22的结果是4的几倍?
解:(1) 因为(-2)2+02+22=4+4=8,8÷4=2,所以其结果是4
的2倍.
(3) 设三个连续整数的中间一个整数为x,请直接写出它们的平方和被
3除的余数.
解:(3) 2.
(2) 设三个连续偶数的中间一个偶数为2x,写出它们的平方和,并说
明是否为4的倍数.
解:(2) 由题意,得另外两个偶数分别为2x-2和2x+2.因为平方和为
(2x-2)2+(2x)2+(2x+2)2=4x2-8x+4+4x2+4x2+8x+4=
12x2+8=4(3x2+2),所以其平方和是4的倍数.
考点六 新定义问题
典例9 如果一个正整数能表示为两个连续偶数的平方差,那么称这个
正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,因此4、
12、20这三个数都是“神秘数”.
(1) 28是“神秘数”吗?为什么?
(2) 设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连
续偶数构造的“神秘数”是4的倍数吗?为什么?
(3) 若长方形相邻两边的长为两个连续偶数,试说明其周长一定为
“神秘数”.
(4) 若将三位数中最大的“神秘数”记为a,两位数中最大的“神秘
数”记为b,求a+b的值.
思路导引 (1) 根据新定义判断求解.(2) 根据新定义列式,再分解
因式说明.(3) 先用k表示长方形的两边的长,再根据(2)中的结论说
明.(4) 利用(2)中的结论列不等式求出a、b的值,再求解.
规范解答 (1) 28是“神秘数”.
因为28=82-62,
所以28是“神秘数”.
(2) 由两个连续偶数构造的“神秘数”是4的倍数.
因为(2k+2)2-(2k)2=4k2+8k+4-4k2=8k+4=4(2k+1),
所以由两个连续偶数构造的“神秘数”是4的倍数.
(3) 设长方形相邻两边的长分别为2k+2、2k(k为正整数),则其周
长为2(2k+2+2k)=8k+4=(2k+2)2-(2k)2.
所以该长方形的周长一定为“神秘数”.
(4) 由(2),得8k+4是“神秘数”.
由8k+4<1000,得k<124.5.
所以k的最大整数值为124.
所以a=8×124+4=996.
由8k+4<100,得k<12.
所以k的最大整数值为11.
所以b=8×11+4=92.
所以a+b=996+92=1088.
现学活用
12. 我们规定: 表示abc, 表示xm+yn.根据这个规定,解答下
列问题:
(1) 计算: ÷ = .
(2) 若代数式 + 为完全平方式,则k= .
(3) 解方程: - =6x2+7.
解:由题意,得(3x-2)(3x+2)-[(x+2)(3x-2)+32]=6x2
+7.整理,得6x2-4x-9=6x2+7,解得x=-4.
-
3或-3
第9章 整式乘法与因式分解
高频考点突破
考点一 单项式与单项式、多项式相乘
典例1 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=
-2.
思路导引 首先根据单项式与多项式相乘的法则去掉括号,然后合并同
类项,最后代入已知的数值计算求值.
规范解答 原式=6a3-12a2+9a-6a3-8a2=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-20×4-9×2=
-98.
现学活用
1. 已知x2-2=y,则x(x-2023y)-y(1-2023x)的值为( A )
A. 2 B. 0 C. -2 D. 1
2. 下列计算中,正确的是( D )
A. 3ab+2b=5ab
B. (-x2)·(-x)2=x4
C. (-2ab2)3=8a3b6
D. 2m(n2-3m2)=2mn2-6m3
A
D
考点二 多项式乘多项式
典例2 如图,某高铁站广场前有一块长为2a+b、宽为a+b的长方形空
地,计划在中间留两个长方形喷泉池(图中涂色部分),两个长方形喷
泉池及周边留有宽度为b的人行通道.
(典例2图)
(1) 求该长方形空地的面积(用含a、b的代数式表示).
(2) 求这两个长方形喷泉池的总面积(用含a、b的代数式表示).
(3) 当a=200,b=100时,求这两个长方形喷泉池的总面积.
思路导引 (1) 根据长方形的面积公式列式并计算求得.(2) 根据
“长为2a+b、宽为a+b的长方形空地”“两个长方形喷泉池及周边留
有宽度为b的人行通道”,进行列式计算.(3) 把a=200,b=100代入
(2)中得到的结果进行计算,即可求得结果.
规范解答 (1) 由题意,得(a+b)(2a+b)=2a2+3ab+b2.
所以该长方形空地的面积为2a2+3ab+b2.
(2) 由题意,得(a+b-2b)(2a+b-3b)=(a-b)(2a-2b)
=2a2-4ab+2b2.
所以这两个长方形喷泉池的总面积为2a2-4ab+2b2.
(3) 当a=200,b=100时,2a2-4ab+2b2=2×2002-4×200×100+
2×1002=20000.
所以这两个长方形喷泉池的总面积为20000.
现学活用
3. 已知a+b=11,ab=1,求(a-2)(b-2)的值.
解:(a-2)(b-2)=ab-2a-2b+4=ab-2(a+b)+4.因为a+b
=11,ab=1,所以原式=1-2×11+4=1-22+4=-17.
4. 甲、乙两个长方形的长、宽如图所示(m为正整数),其面积分别为
S1、S2.
(1) 请用含m的代数式分别表示S1、S2.
解:(1) S1=(m+7)(m+1)=m2+8m+7;S2=(m+4)(m+
2)=m2+6m+8.
(2) 若一个正方形的周长等于甲、乙两个长方形的周长之和,设该正
方形的面积为S3,试探究S3与2(S1+S2)的差是否为常数?若是常数,
求出这个常数;若不是常数,请说明理由.
(第4题)
解:(2) 是常数.设该正方形的边长为a.根据题意,得4a=2(m+7+
m+1)+2(m+4+m+2),解得a=2m+7.所以S3=(2m+7)2.所以
S3-2(S1+S2)=(2m+7)2-2(m2+8m+7+m2+6m+8)=4m2
+28m+49-4m2-28m-30=19.所以S3 与 2(S1+S2)的差是常数19.
考点三 乘法公式
典例3 (2023·盐城)先化简,再求值:(a+3b)2+(a+3b)(a-
3b),其中a=2,b=-1.
思路导引 依据题意,利用完全平方公式和平方差公式将原式进行化
简,再将a、b的值代入计算即可.
规范解答 原式=a2+6ab+9b2+a2-9b2=2a2+6ab.
当a=2,b=-1时,原式=2×22+6×2×(-1)=8-12=-4.
现学活用
5. 先化简,再求值:4(x+1)2-4(x-1)·(x+1)+(1-x)2,其
中x=-2.
解:原式=4(x+1)2+4(1-x)(x+1)+(1-x)2=[2(x+1)
+1-x]2=(x+3)2=x2+6x+9.把x=-2代入,得原式=(-2)2+
6×(-2)+9=4-12+9=1.
典例4 通常,用两种不同的方法计算同一个图形的面积可以得到一个
恒等式.如图,将一个边长为a+b的正方形分割成四个部分(两个正方
形和两个长方形),请观察图形,解答下列问题:
(1) 根据图中条件,用两种方法表示该图形的总面积,可得如下
公式: .
(2) 如果图中的a、b(a>b>0)满足a2+b2=70,
ab=15,求a+b的值.
(典例4图)
(3) 已知(x+9)2+(x-1)2=124,求(x+9)(x-1)的值.
(典例4图)
思路导引 (1) 根据该图形的总面积为(a+b)2或a2+2ab+b2可得
结果.(2) 由(1)中的结果,可得(a+b)2=a2+2ab+b2,根据a2+
b2=70,ab=15,可求得(a+b)2的值,即可求a+b的值.(3) 设x+9
=a,x-1=b,则可求得a-b的值,根据(a-b)2=a2+b2-2ab代入
计算可求得ab=12,即可求得(x+9)(x-1)的值.
规范解答 (1) 该图形的总面积为(a+b)2或a2+2ab+b2.故填(a+
b)2=a2+2ab+b2.
(2) 由(1)中的结果,可得(a+b)2=a2+2ab+b2,
所以当a2+b2=70,ab=15时,(a+b)2=70+2×15=100.
又因为a>b>0,所以a+b=10.
(3) 设x+9=a,x-1=b,则(x+9)2+(x-1)2=a2+b2=124.
所以a-b=(x+9)-(x-1)=10.
因为(a-b)2=a2+b2-2ab,a-b=10,a2+b2=124,所以100=124
-2ab.
所以ab=12.
所以(x+9)(x-1)=ab=12.
现学活用
6. 如图①所示为一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其
平均分成四个小长方形,然后用这四个小长方形拼成的一个“回”形正
方形(如图②).
(1) 观察图②,可以得到(a+b)2-(a-b)2= .
4ab
(2) 当(x-8)(15-x)=6时,求(2x-23)2的值.
(第6题)
解:设x-8=a,15-x=b,则ab=(x-8)(15-x)=6.所以a+b=
x-8+15-x=7,a-b=2x-23.因为(a+b)2-(a-b)2=4ab,所
以(a-b)2=(a+b)2-4ab=72-4×6=25,即(2x-23)2=25.
考点四 因式分解
典例5 将9(a-b)2+12(a2-b2)+4(a+b)2分解因式的结果是
( )
A. (5a-b)2
B. (5a+b)2
C. (5a-2b)2
D. (3a-2b)(3a+2b)
思路导引 把9(a-b)2、4(a+b)2分别看成是[3(a-b)]2、[2(a
+b)]2,把12(a2-b2)看成是3(a-b)与2(a+b)的积的2倍,再
直接利用完全平方公式分解因式得出结果.
规范解答 原式=[3(a-b)+2(a+b)]2=(5a-b)2.故选A.
现学活用
7. 多项式m2-4与m2-4m+4有相同的因式为( B )
A. m+2 B. m-2 C. m+4 D. m-4
B
典例6 分解因式:
(1) 3a2-6ab+3b2.
(2) x2(m-2)+y2(2-m).
思路导引 (1) 先提公因式,再利用完全平方公式继续分解即可.
(2) 先提公因式,再利用平方差公式继续分解即可.
规范解答 (1) 原式=3(a2-2ab+b2)=3(a-b)2.
(2) 原式=(m-2)(x2-y2)=(m-2)(x+y)(x-y).
方法归纳
分解因式的一般步骤
1. 如果多项式的首项为负,应先提取负号;2. 如果多项式的各项
含有公因式,那么先提取公因式,再进一步分解因式;3. 如果各项没
有公因式,那么可观察该多项式是否具有完全平方或平方差公式的特
征,尝试运用公式法来分解;4. 如果用上述方法不能分解,再尝试用
分组法、拆项法、补项法、十字交叉法来分解;5. 注意检验分解因式
的最终结果(不能再继续分解).
现学活用
8. 分解因式:
(1) 3b(a-b)+a2-ab.
解:原式=3b(a-b)+a(a-b)=(a-b)(3b+a).
(2) (x2+1)2-4x2.
解:原式=(x2+1+2x)(x2+1-2x)=(x+1)2(x-1)2.
9. 若一个三角形的三边长分别为a、b、c,且满足a2+2b2+c2-2ab-
2bc=0.试判断该三角形的形状,并说明理由.
解:该三角形是等边三角形.
理由:因为a2+2b2+c2-2ab-2bc=0,所以a2-2ab+b2+b2-2bc+c2
=0.所以(a-b)2+(b-c)2=0.所以a-b=0且b-c=0.所以a=b且b
=c,即a=b=c.所以该三角形是等边三角形.
典例7 若a2(b+c)=b2(a+c)=2023,a≠b,则abc的值为( )
A. 2023 B. 1011
C. -2023 D. 2024
思路导引 将已知等式利用提公因式法进行整体变形,进而探求abc
的值.
规范解答 因为a2(b+c)=b2(a+c)=2023,所以a2(b+c)-b2
(a+c)=0,即a2b+a2c-ab2-b2c=0.整理,得ab(a-b)+c(a+
b)(a-b)=0.所以(a-b)(ab+ac+bc)=0.因为a≠b,所以a-
b≠0.所以ab+ac+bc=0,即ab+bc=-ac.因为b2(a+c)=b(ab+
bc)=2023,所以b·(-ac)=2023.所以abc=-2023.故选C.
现学活用
10. 已知x-y=2,y-z=-1,求x2+y2+z2-xy-yz-xz的值.
解:因为x-y=2,y-z=-1,所以x-z=(x-y)+(y-z)=1.所
以x2+y2+z2-xy-yz-xz=(2x2+2y2+2z2-2xy-2yz-2xz)=[(x
-y)2+(y-z)2+(x-z)2]=×[22+(-1)2+12]=×6=3.
考点五 代数推理题
典例8 小敏和小华对一些四位数(a、b、c、d均为不超过9的正整
数)进行了观察、猜想,请你帮助他们一起完成探究.
(1) 这个四位数可用含a、b、c、d的代数式表示为
.
(2) 小敏尝试将一些四位数倒排后,再与原数相加,发现和都为11的
倍数.如1234+4321=5555=505×11,4258+8524=12782=1162×11.
请仿照小敏的做法再举一个具体的例子: .你认
为上述结论对于一般的+也成立吗?请说明理由.
(3) 小华认为如果一个四位数的四个数字之和是9的倍数,那么这个
四位数也是9的倍数.如3231=359×9,4455=495×9,6948=772×9.请
仿照小华的做法再举一个具体的例子: .你认为
上述结论对于一般的(a+b+c+d=9k,k是正整数)也成立吗?
请说明理由.
思路导引 (1) 用多位数的表示方法直接表示即可.(2) 用多位数的
表示方法表示出这两个四位数相加,合并同类项,提取公因式即可.
(3) 用多位数的表示方法表示出四位数,然后用拆项法,拆出四位数
的各位数字之和,整理可得结论成立.
规范解答 (1) 1000a+100b+10c+d.
(2) 答案不唯一,如2345+5432=7777=707×11.
成立.
理由:因为+=(1000a+100b+10c+d)+(1000d+100c+
10b+a)=1001a+110b+110c+1001d=11(91a+91d+10b+10c),
91a+91d+10b+10c是整数,
所以+的结果为11的倍数.
(3) 答案不唯一,如8181=909×9.
成立.
理由:因为=1000a+100b+10c+d=(999a+99b+9c)+(a+b
+c+d)=9(111a+11b+c)+9k=9(111a+11b+c+k),111a+
11b+c+k是整数,
所以为9的倍数.
现学活用
11. 发现:任意三个连续偶数的平方和是4的倍数.
(1) (-2)2+02+22的结果是4的几倍?
解:(1) 因为(-2)2+02+22=4+4=8,8÷4=2,所以其结果是4
的2倍.
(3) 设三个连续整数的中间一个整数为x,请直接写出它们的平方和被
3除的余数.
解:(3) 2.
(2) 设三个连续偶数的中间一个偶数为2x,写出它们的平方和,并说
明是否为4的倍数.
解:(2) 由题意,得另外两个偶数分别为2x-2和2x+2.因为平方和为
(2x-2)2+(2x)2+(2x+2)2=4x2-8x+4+4x2+4x2+8x+4=
12x2+8=4(3x2+2),所以其平方和是4的倍数.
考点六 新定义问题
典例9 如果一个正整数能表示为两个连续偶数的平方差,那么称这个
正整数为“神秘数”.如4=22-02,12=42-22,20=62-42,因此4、
12、20这三个数都是“神秘数”.
(1) 28是“神秘数”吗?为什么?
(2) 设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连
续偶数构造的“神秘数”是4的倍数吗?为什么?
(3) 若长方形相邻两边的长为两个连续偶数,试说明其周长一定为
“神秘数”.
(4) 若将三位数中最大的“神秘数”记为a,两位数中最大的“神秘
数”记为b,求a+b的值.
思路导引 (1) 根据新定义判断求解.(2) 根据新定义列式,再分解
因式说明.(3) 先用k表示长方形的两边的长,再根据(2)中的结论说
明.(4) 利用(2)中的结论列不等式求出a、b的值,再求解.
规范解答 (1) 28是“神秘数”.
因为28=82-62,
所以28是“神秘数”.
(2) 由两个连续偶数构造的“神秘数”是4的倍数.
因为(2k+2)2-(2k)2=4k2+8k+4-4k2=8k+4=4(2k+1),
所以由两个连续偶数构造的“神秘数”是4的倍数.
(3) 设长方形相邻两边的长分别为2k+2、2k(k为正整数),则其周
长为2(2k+2+2k)=8k+4=(2k+2)2-(2k)2.
所以该长方形的周长一定为“神秘数”.
(4) 由(2),得8k+4是“神秘数”.
由8k+4<1000,得k<124.5.
所以k的最大整数值为124.
所以a=8×124+4=996.
由8k+4<100,得k<12.
所以k的最大整数值为11.
所以b=8×11+4=92.
所以a+b=996+92=1088.
现学活用
12. 我们规定: 表示abc, 表示xm+yn.根据这个规定,解答下
列问题:
(1) 计算: ÷ = .
(2) 若代数式 + 为完全平方式,则k= .
(3) 解方程: - =6x2+7.
解:由题意,得(3x-2)(3x+2)-[(x+2)(3x-2)+32]=6x2
+7.整理,得6x2-4x-9=6x2+7,解得x=-4.
-
3或-3
同课章节目录
