解直角三角形的应用(湖北省恩施土家族苗族自治州宣恩县)
文档属性
| 名称 | 解直角三角形的应用(湖北省恩施土家族苗族自治州宣恩县) |
|
|
| 格式 | rar | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-08 00:00:00 | ||
图片预览



文档简介
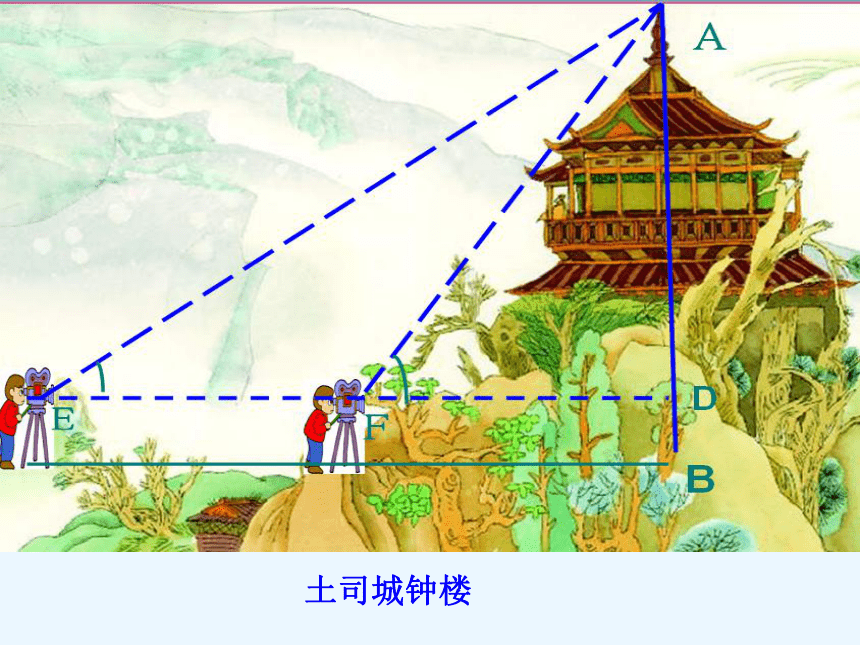
课件19张PPT。 解直角三角形的应用宣恩县高罗民族中学 彭 丹 土司城钟楼◆.地位和作用
运用解直角三角形知识解应用题,在日常生活、生产中有着广泛的应用,主要涉及测量、航空、航海、工程等领域,也是 学业考试的重要内容之一,所以,我们应该学好这个内容。◆. 本课时复习目标
⑴ 进一步巩固三角函数 的有关概念 , 特殊角的
三角函数值
⑵能运用三角函数解与直角三角形有关的实
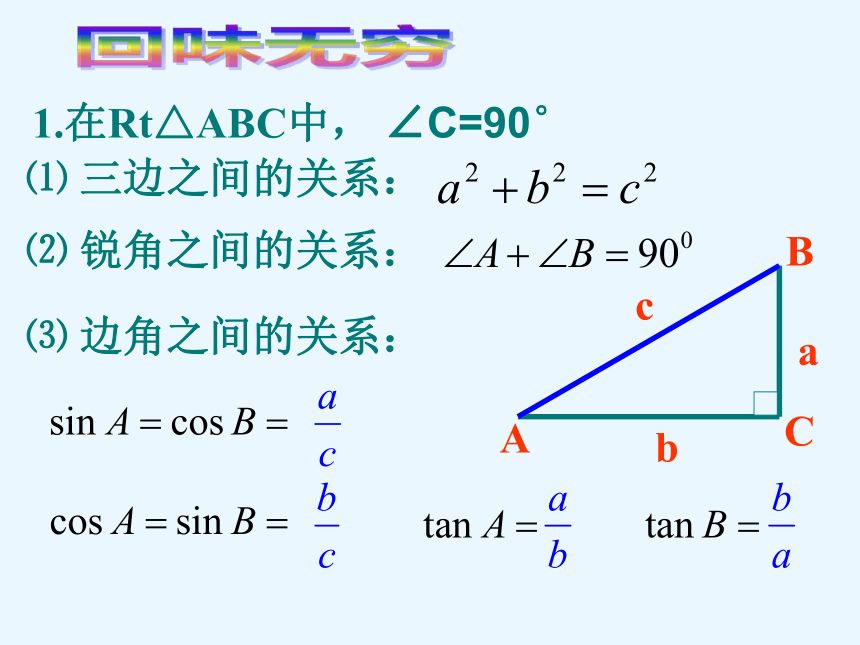
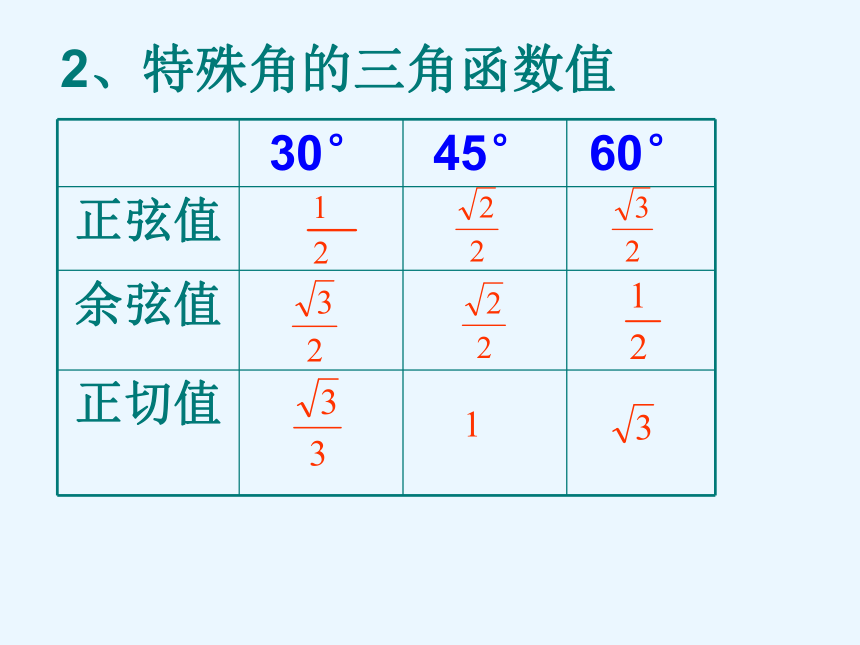
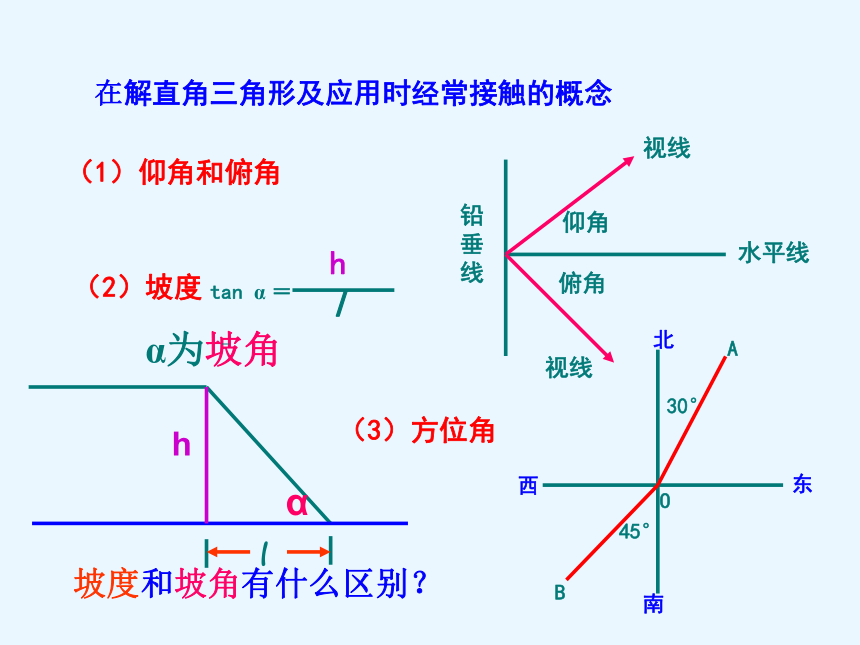
际问 题回味无穷1.在Rt△ABC中, ∠C=90。 ⑴ 三边之间的关系:⑵ 锐角之间的关系:⑶ 边角之间的关系:2、特殊角的三角函数值在解直角三角形及应用时经常接触的概念(1)仰角和俯角(3)方位角α为坡角坡度和坡角有什么区别? 星期天,小华去图书超市购书,他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为350,则二楼的高度BC段约是 ________mABC3508基础演练4.6 选用数据:cos35o=0.8192 sin35o=0.5736 tan35o=0.7002(保留一位小数)1、恩施城区在“城市规划改造”中计划在城内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元 B、225a元 C、150a元 D、300a元 30米20米150°ABCD典例剖析C分析:求一般三角形面积,关键求出已知边的高,再用面积公式求出。AO 2、如图, 灯塔A周围1000米处水域内有礁石,一船由西向东航行,在O处测得灯在北偏东740方向线上,这时OA相距4200米,如果不改变航行方向,此船是否有触礁的危险?(供选用的数据:cos740=0.2756,sin740=0.9613,tan740=3.487(精确到个位数)分析:船是否触礁,主要构造直角三角形,关键求灯塔A到航线的最短距离。答:此船按原航向继续航行没有触礁的危险。
已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.FE解: 分别过点D、C作DF⊥AB于F,CE⊥AB于E∴ FE=DC=4在Rt△ADF中,∠A=60otan60o=在Rt △ CBE中,∠B=45o∴ AB=AF+FE+EB= +4+4 =8+∴ AF=∴ EB=EC=4巩固提高 恩施连珠塔 如图,在A点测得恩施连珠塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知山高DC=48m,求塔高BD.( 结果保留整数, = 1.732) ABCDαβ解: 设BD=x米则 CB =48+X在Rt△ABC中, ∠α=60o ∴ tan60o= ∴ X≈35(米)所以塔高约为35米分析:要求塔高,想到方程思想,关键找出等量关系∴ = ∵在Rt△ADC中,∠β=45o ∠ADC=45° ∴AC=DC=48米能力拓展小结这节课主要是运用三角函数解应用题,通过
学习后,怎样去解这样的问题呢?你有那些
感想?有什么收获?还有什么困惑? ◆ 运用三角函数解应用题时,有时适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决.
◆ 要注重数形结合,把实际问题转化为数学问题,正确选择三角函数
◆充分利用方程思想,使问题简化谢谢合作
2、 我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的第一层起照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米。
A、15sin550 B、15cos550 C、15tan550 C550如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,在Rt△CDB中, CD=20 , CB=25,3004025∴CD=20,答:(略) 一船在海上B处以每小时30海里的速度,沿南偏东22o方向航行,同时在B 处测得灯塔A 在南偏东52o的方向上,航行2小时后到达C处,又测得灯塔A在北偏东68o方向上,求AC的距离。解:依题意得 ∠CBD=22°∠ABD=52°
∴∠ABC = 52 o - 22°=30°∴∠BCA=22°+68°=90O∵ BC=2×30=60(海里)∴ AC=BC·tan30o =60× / 3
= 20 (海里)答: AC的距离是20 海里。北B东AC 22°68°D52°东
运用解直角三角形知识解应用题,在日常生活、生产中有着广泛的应用,主要涉及测量、航空、航海、工程等领域,也是 学业考试的重要内容之一,所以,我们应该学好这个内容。◆. 本课时复习目标
⑴ 进一步巩固三角函数 的有关概念 , 特殊角的
三角函数值
⑵能运用三角函数解与直角三角形有关的实
际问 题回味无穷1.在Rt△ABC中, ∠C=90。 ⑴ 三边之间的关系:⑵ 锐角之间的关系:⑶ 边角之间的关系:2、特殊角的三角函数值在解直角三角形及应用时经常接触的概念(1)仰角和俯角(3)方位角α为坡角坡度和坡角有什么区别? 星期天,小华去图书超市购书,他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为350,则二楼的高度BC段约是 ________mABC3508基础演练4.6 选用数据:cos35o=0.8192 sin35o=0.5736 tan35o=0.7002(保留一位小数)1、恩施城区在“城市规划改造”中计划在城内一块如图所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元 B、225a元 C、150a元 D、300a元 30米20米150°ABCD典例剖析C分析:求一般三角形面积,关键求出已知边的高,再用面积公式求出。AO 2、如图, 灯塔A周围1000米处水域内有礁石,一船由西向东航行,在O处测得灯在北偏东740方向线上,这时OA相距4200米,如果不改变航行方向,此船是否有触礁的危险?(供选用的数据:cos740=0.2756,sin740=0.9613,tan740=3.487(精确到个位数)分析:船是否触礁,主要构造直角三角形,关键求灯塔A到航线的最短距离。答:此船按原航向继续航行没有触礁的危险。
已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.FE解: 分别过点D、C作DF⊥AB于F,CE⊥AB于E∴ FE=DC=4在Rt△ADF中,∠A=60otan60o=在Rt △ CBE中,∠B=45o∴ AB=AF+FE+EB= +4+4 =8+∴ AF=∴ EB=EC=4巩固提高 恩施连珠塔 如图,在A点测得恩施连珠塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知山高DC=48m,求塔高BD.( 结果保留整数, = 1.732) ABCDαβ解: 设BD=x米则 CB =48+X在Rt△ABC中, ∠α=60o ∴ tan60o= ∴ X≈35(米)所以塔高约为35米分析:要求塔高,想到方程思想,关键找出等量关系∴ = ∵在Rt△ADC中,∠β=45o ∠ADC=45° ∴AC=DC=48米能力拓展小结这节课主要是运用三角函数解应用题,通过
学习后,怎样去解这样的问题呢?你有那些
感想?有什么收获?还有什么困惑? ◆ 运用三角函数解应用题时,有时适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决.
◆ 要注重数形结合,把实际问题转化为数学问题,正确选择三角函数
◆充分利用方程思想,使问题简化谢谢合作
2、 我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的第一层起照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米。
A、15sin550 B、15cos550 C、15tan550 C550如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,在Rt△CDB中, CD=20 , CB=25,3004025∴CD=20,答:(略) 一船在海上B处以每小时30海里的速度,沿南偏东22o方向航行,同时在B 处测得灯塔A 在南偏东52o的方向上,航行2小时后到达C处,又测得灯塔A在北偏东68o方向上,求AC的距离。解:依题意得 ∠CBD=22°∠ABD=52°
∴∠ABC = 52 o - 22°=30°∴∠BCA=22°+68°=90O∵ BC=2×30=60(海里)∴ AC=BC·tan30o =60× / 3
= 20 (海里)答: AC的距离是20 海里。北B东AC 22°68°D52°东
