18.2.1矩形的性质 课件(共26张PPT)
文档属性
| 名称 | 18.2.1矩形的性质 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
特殊的平行四边形
18.2.1 矩形的性质
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
学习目标
对边平行
对边相等
对角相等
对角线互相平分
平行四边形的性质有哪些?
知识回顾
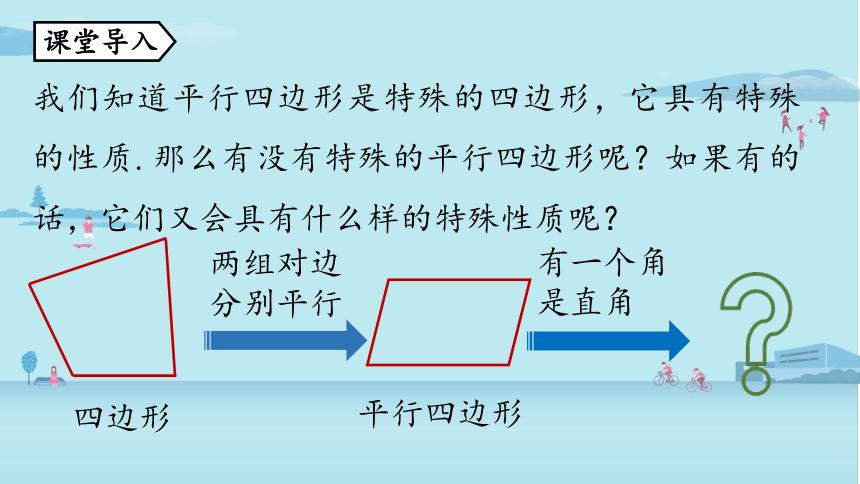
我们知道平行四边形是特殊的四边形,它具有特殊的性质. 那么有没有特殊的平行四边形呢?如果有的话,它们又会具有什么样的特殊性质呢?
两组对边分别平行
四边形
平行四边形
有一个角
是直角
课堂导入
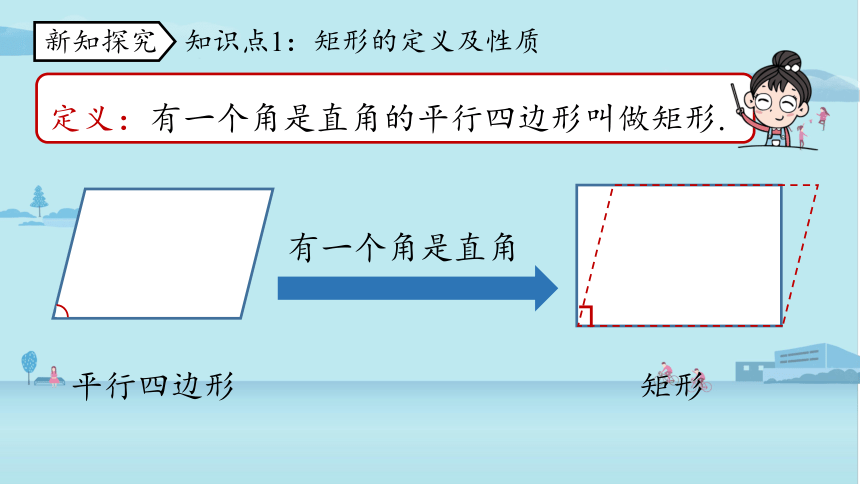
平行四边形
矩形
有一个角是直角
┐
知识点1:矩形的定义及性质
新知探究
定义:有一个角是直角的平行四边形叫做矩形.
1. 矩形必须具备两个条件:
2. 矩形的定义既可以作为矩形的性质,也可以作为判定一个四边形是矩形的方法.
注意:矩形是特殊的平行四边形,但平行四边形不一定是矩形.
①是平行四边形;
②有一个角是直角.
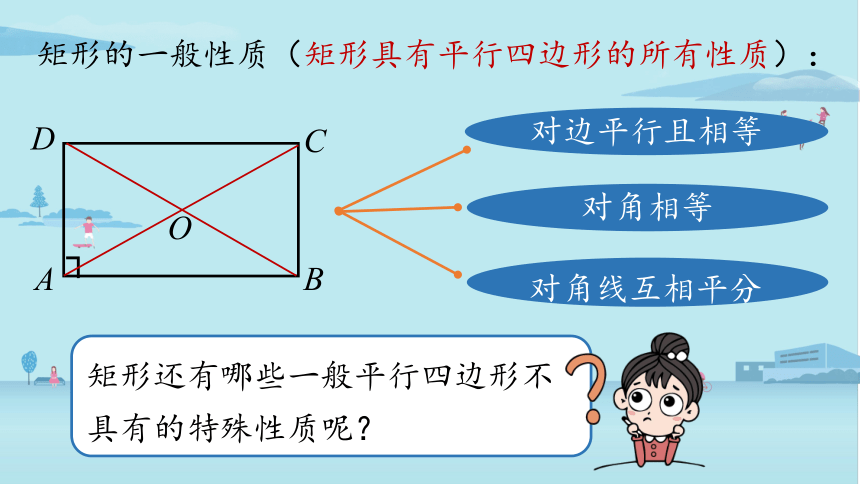
矩形还有哪些一般平行四边形不具有的特殊性质呢?
矩形的一般性质(矩形具有平行四边形的所有性质):
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
┐
O
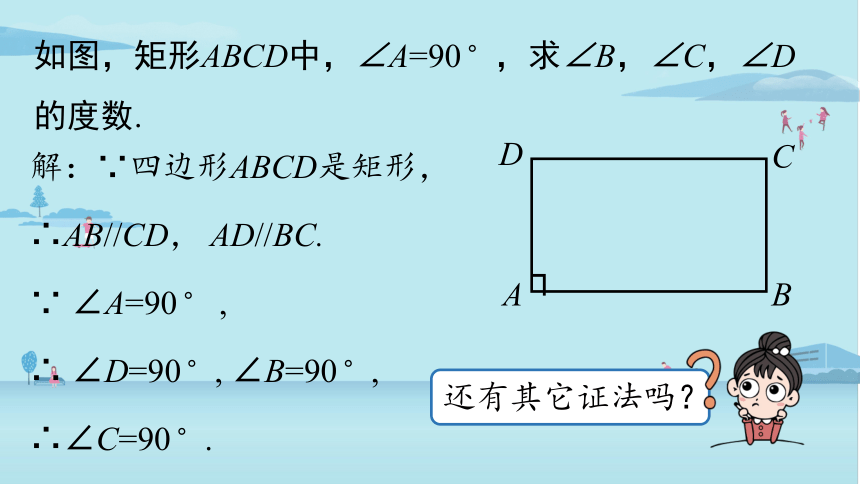
如图,矩形ABCD中,∠A=90 ,求∠B,∠C,∠D 的度数.
解:∵四边形ABCD是矩形,
∵ ∠A=90 ,
∴∠C=90 .
A
B
D
C
┐
还有其它证法吗?
∴AB//CD, AD//BC.
∴ ∠D=90 , ∠B=90 ,
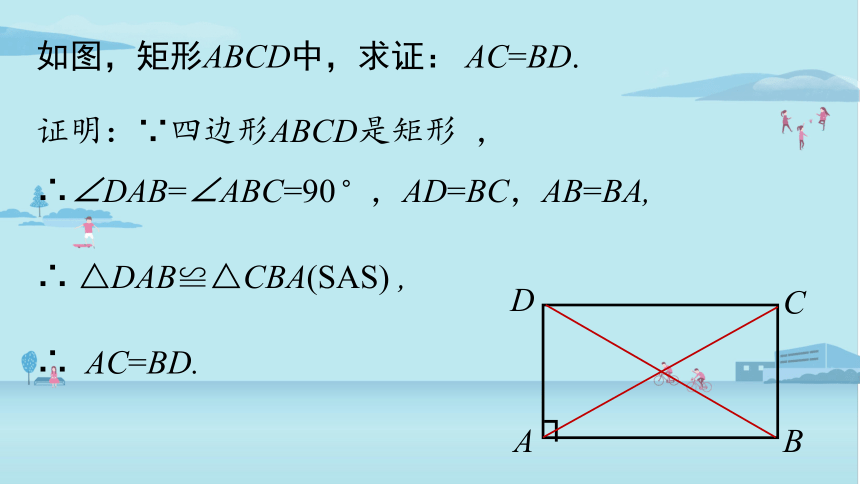
如图,矩形ABCD中,求证: AC=BD.
证明:∵四边形ABCD是矩形 ,
∴∠DAB=∠ABC=90 ,AD=BC,AB=BA,
∴ △DAB≌△CBA(SAS) ,
A
B
D
C
┐
∴ AC=BD.
矩形是轴对称图形吗?如果是,它有几条对称轴呢?
A
B
D
C
┐
是.它有两条对称轴,分别是对边中点的连线所在的直线.
性质 数学语言 图形
角
对角线
对称性
矩形的四个角都是直角
矩形的对角线相等
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=9 .
∴ AC=BD.
∵四边形ABCD是矩形,
矩形是轴对称图形,它有两条对称轴.
A
B
D
C
A
B
D
C
O
1.对比平行四边形,下列选项中是矩形具有的特殊性质有( ).
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
跟踪训练
新知探究
一般性质
一般性质
一般性质
2.已知四边形ABCD是矩形,其中AB=8 , BC=6,则BD 的长为 .
10
∵ AB=8 ,BC=6,
∴ AC ==10,
∴BD = AC ,∠ABC=90°.
A
B
D
C
┐
O
解:∵四边形ABCD是矩形,
∴BD = 10.
矩形的对角线相等
A
B
D
C
┐
O
思考 如图,矩形ABCD的对角线AC, BD相交于点O. 在Rt△ABC中, BO是斜边AC上的中线,BO 与AC 有什么关系?
知识点2:直角三角形斜边上中线的性质
新知探究
猜想BO=AC.
如图,矩形ABCD的对角线AC, BD相交于点O.
求证:BO=AC.
解:∵四边形ABCD是矩形,
∴,BD=AC ,
∴
A
B
D
C
┐
O
通过以上证明,我们得到直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.
3.在Rt△ABC中, ∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线, AD=2, CE=5,则CD=( ).
A.2 B.3
C.4 D.
C
跟踪训练
新知探究
直角三角形斜边上的中线等于斜边的一半.
解析: ∵在Rt△ABC中, ∠ACB=90 ,
CE为AB边上的中线, CE=5,
∴AE=CE=5.
∵AD=2,
∴DE=3.
∵CD为AB边上的高,
∴在Rt△CDE中,
1.下列性质中,矩形不一定具有的性质是( ).
A.对角线相等
B.四个内角相等
C.对角线垂直
D.是轴对称图形
C
随堂练习
对角线互相平分且相等
四个内角均为90°
有两条对称轴
2.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ADB=34°,则∠BAO的度数是( )
A.46° B.54°
C.56° D.60°
C
B
C
A
D
O
34°
34°
56°
3. 矩形 ABCD 中,对角线 AC, BD 相交于点 O,请填写下列空格.
(1)若OA=4,则BD= .
8
(2)若∠DAO=60 , AD=3,则
AC= .
6
A
B
D
C
O
熟记矩形的性质
4.如图,在△ABC中,AD是高,E ,F分别是边AB , AC的中点.若AB=10,AC=8,求四边形AEDF的周长;
解:∵AD是△ABC的高,E, F分别是
边AB, AC的中点,
∴DE=AE= AB= ×10=5,
DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=18.
1. 如图,矩形ABCD的对角线AC与BD相交于点O, ∠ADB=30 ,AB=4,则OC=( ).
A.5 B.4 C.3.5 D.3
B
解析: ∵四边形ABCD是矩形, ∠ADB=30 ,
∴AC=BD, ∠ABD=60 .
A
B
D
C
O
拓展提升
∴ OA= OB= AB=4 ,
∴ OC= OA=4 ,
2.如图,矩形 ABCD 中,E 为 AD 上一点, EF⊥CE 交AB 于点 F,若 DE=2,矩形 ABCD 的周长为 16,且CE=EF,求 AE 的长.
解:∵四边形 ABCD 为矩形,
B
C
A
D
┐
E
F
∴ ∠A=∠D=90 .
∵EF⊥CE,
∴ ∠AEF+∠DEC=90 .
∵ ∠A=90 ,
∴ ∠AEF+∠AFE=90 ,
∴ ∠DEC=∠AFE.
∵∠A=∠D=90 ,∠AFE=∠DEC,EF=CE,
∴△AEF≌△DCE(AAS),
∵ 矩形 ABCD 的周长为16,
∴ AD+CD=8.
∵ DE=2,AE=DC,
∴AE=DC.
∴ 2+AE+AE=8, ∴ AE=3.
B
C
A
D
┐
E
F
矩形
概念
特殊性质
有一个角是直角的平行四边形是矩形.
①四个角都是直角
②对角线相等
③轴对称图形
直角三角形斜边上的中线等于斜边的一半.
课堂小结
特殊的平行四边形
18.2.1 矩形的性质
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
学习目标
对边平行
对边相等
对角相等
对角线互相平分
平行四边形的性质有哪些?
知识回顾
我们知道平行四边形是特殊的四边形,它具有特殊的性质. 那么有没有特殊的平行四边形呢?如果有的话,它们又会具有什么样的特殊性质呢?
两组对边分别平行
四边形
平行四边形
有一个角
是直角
课堂导入
平行四边形
矩形
有一个角是直角
┐
知识点1:矩形的定义及性质
新知探究
定义:有一个角是直角的平行四边形叫做矩形.
1. 矩形必须具备两个条件:
2. 矩形的定义既可以作为矩形的性质,也可以作为判定一个四边形是矩形的方法.
注意:矩形是特殊的平行四边形,但平行四边形不一定是矩形.
①是平行四边形;
②有一个角是直角.
矩形还有哪些一般平行四边形不具有的特殊性质呢?
矩形的一般性质(矩形具有平行四边形的所有性质):
对边平行且相等
对角相等
对角线互相平分
A
B
D
C
┐
O
如图,矩形ABCD中,∠A=90 ,求∠B,∠C,∠D 的度数.
解:∵四边形ABCD是矩形,
∵ ∠A=90 ,
∴∠C=90 .
A
B
D
C
┐
还有其它证法吗?
∴AB//CD, AD//BC.
∴ ∠D=90 , ∠B=90 ,
如图,矩形ABCD中,求证: AC=BD.
证明:∵四边形ABCD是矩形 ,
∴∠DAB=∠ABC=90 ,AD=BC,AB=BA,
∴ △DAB≌△CBA(SAS) ,
A
B
D
C
┐
∴ AC=BD.
矩形是轴对称图形吗?如果是,它有几条对称轴呢?
A
B
D
C
┐
是.它有两条对称轴,分别是对边中点的连线所在的直线.
性质 数学语言 图形
角
对角线
对称性
矩形的四个角都是直角
矩形的对角线相等
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=9 .
∴ AC=BD.
∵四边形ABCD是矩形,
矩形是轴对称图形,它有两条对称轴.
A
B
D
C
A
B
D
C
O
1.对比平行四边形,下列选项中是矩形具有的特殊性质有( ).
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
跟踪训练
新知探究
一般性质
一般性质
一般性质
2.已知四边形ABCD是矩形,其中AB=8 , BC=6,则BD 的长为 .
10
∵ AB=8 ,BC=6,
∴ AC ==10,
∴BD = AC ,∠ABC=90°.
A
B
D
C
┐
O
解:∵四边形ABCD是矩形,
∴BD = 10.
矩形的对角线相等
A
B
D
C
┐
O
思考 如图,矩形ABCD的对角线AC, BD相交于点O. 在Rt△ABC中, BO是斜边AC上的中线,BO 与AC 有什么关系?
知识点2:直角三角形斜边上中线的性质
新知探究
猜想BO=AC.
如图,矩形ABCD的对角线AC, BD相交于点O.
求证:BO=AC.
解:∵四边形ABCD是矩形,
∴,BD=AC ,
∴
A
B
D
C
┐
O
通过以上证明,我们得到直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.
3.在Rt△ABC中, ∠ACB=90 ,CD为AB边上的高,CE为AB边上的中线, AD=2, CE=5,则CD=( ).
A.2 B.3
C.4 D.
C
跟踪训练
新知探究
直角三角形斜边上的中线等于斜边的一半.
解析: ∵在Rt△ABC中, ∠ACB=90 ,
CE为AB边上的中线, CE=5,
∴AE=CE=5.
∵AD=2,
∴DE=3.
∵CD为AB边上的高,
∴在Rt△CDE中,
1.下列性质中,矩形不一定具有的性质是( ).
A.对角线相等
B.四个内角相等
C.对角线垂直
D.是轴对称图形
C
随堂练习
对角线互相平分且相等
四个内角均为90°
有两条对称轴
2.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ADB=34°,则∠BAO的度数是( )
A.46° B.54°
C.56° D.60°
C
B
C
A
D
O
34°
34°
56°
3. 矩形 ABCD 中,对角线 AC, BD 相交于点 O,请填写下列空格.
(1)若OA=4,则BD= .
8
(2)若∠DAO=60 , AD=3,则
AC= .
6
A
B
D
C
O
熟记矩形的性质
4.如图,在△ABC中,AD是高,E ,F分别是边AB , AC的中点.若AB=10,AC=8,求四边形AEDF的周长;
解:∵AD是△ABC的高,E, F分别是
边AB, AC的中点,
∴DE=AE= AB= ×10=5,
DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=18.
1. 如图,矩形ABCD的对角线AC与BD相交于点O, ∠ADB=30 ,AB=4,则OC=( ).
A.5 B.4 C.3.5 D.3
B
解析: ∵四边形ABCD是矩形, ∠ADB=30 ,
∴AC=BD, ∠ABD=60 .
A
B
D
C
O
拓展提升
∴ OA= OB= AB=4 ,
∴ OC= OA=4 ,
2.如图,矩形 ABCD 中,E 为 AD 上一点, EF⊥CE 交AB 于点 F,若 DE=2,矩形 ABCD 的周长为 16,且CE=EF,求 AE 的长.
解:∵四边形 ABCD 为矩形,
B
C
A
D
┐
E
F
∴ ∠A=∠D=90 .
∵EF⊥CE,
∴ ∠AEF+∠DEC=90 .
∵ ∠A=90 ,
∴ ∠AEF+∠AFE=90 ,
∴ ∠DEC=∠AFE.
∵∠A=∠D=90 ,∠AFE=∠DEC,EF=CE,
∴△AEF≌△DCE(AAS),
∵ 矩形 ABCD 的周长为16,
∴ AD+CD=8.
∵ DE=2,AE=DC,
∴AE=DC.
∴ 2+AE+AE=8, ∴ AE=3.
B
C
A
D
┐
E
F
矩形
概念
特殊性质
有一个角是直角的平行四边形是矩形.
①四个角都是直角
②对角线相等
③轴对称图形
直角三角形斜边上的中线等于斜边的一半.
课堂小结
