2023-2024学年人教版八年级数学下册18.2 矩形 同步练习 (无答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册18.2 矩形 同步练习 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 00:00:00 | ||
图片预览

文档简介
八年级下学期矩形专题测试
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在矩形中,O是对角线,的交点,于点E,若,,则的长为( )
A. B. C. D.
2.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A. B.
C. D.
3.如图,在矩形ABCD中,点E在AD上,且EC平分,,,则DE的长为( )
A. B. C. D.
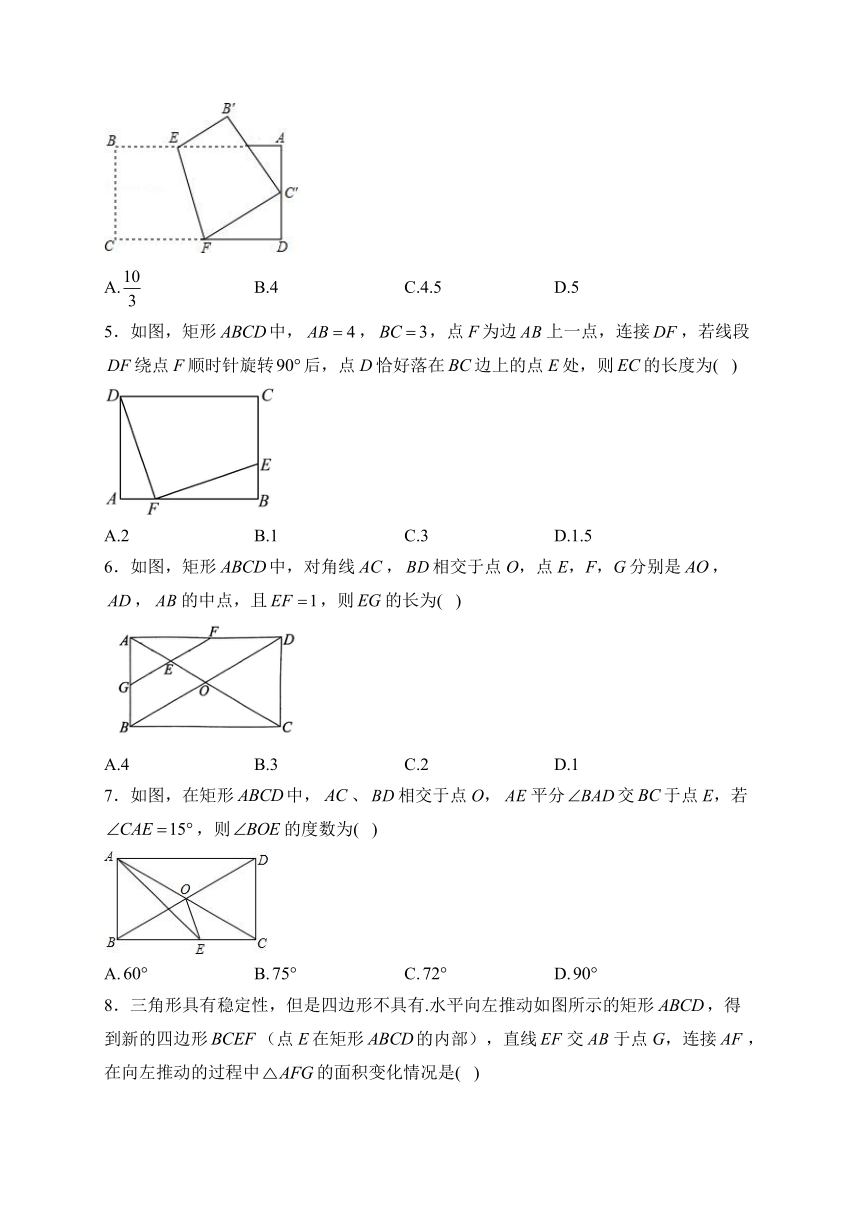
4.如图,将矩形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,,则的长为( )
A. B.4 C.4.5 D.5
5.如图,矩形中,,,点F为边上一点,连接,若线段绕点F顺时针旋转后,点D恰好落在边上的点E处,则的长度为( )
A.2 B.1 C.3 D.1.5
6.如图,矩形中,对角线,相交于点O,点E,F,G分别是,,的中点,且,则的长为( )
A.4 B.3 C.2 D.1
7.如图,在矩形中,、相交于点O,平分交于点E,若,则的度数为( )
A. B. C. D.
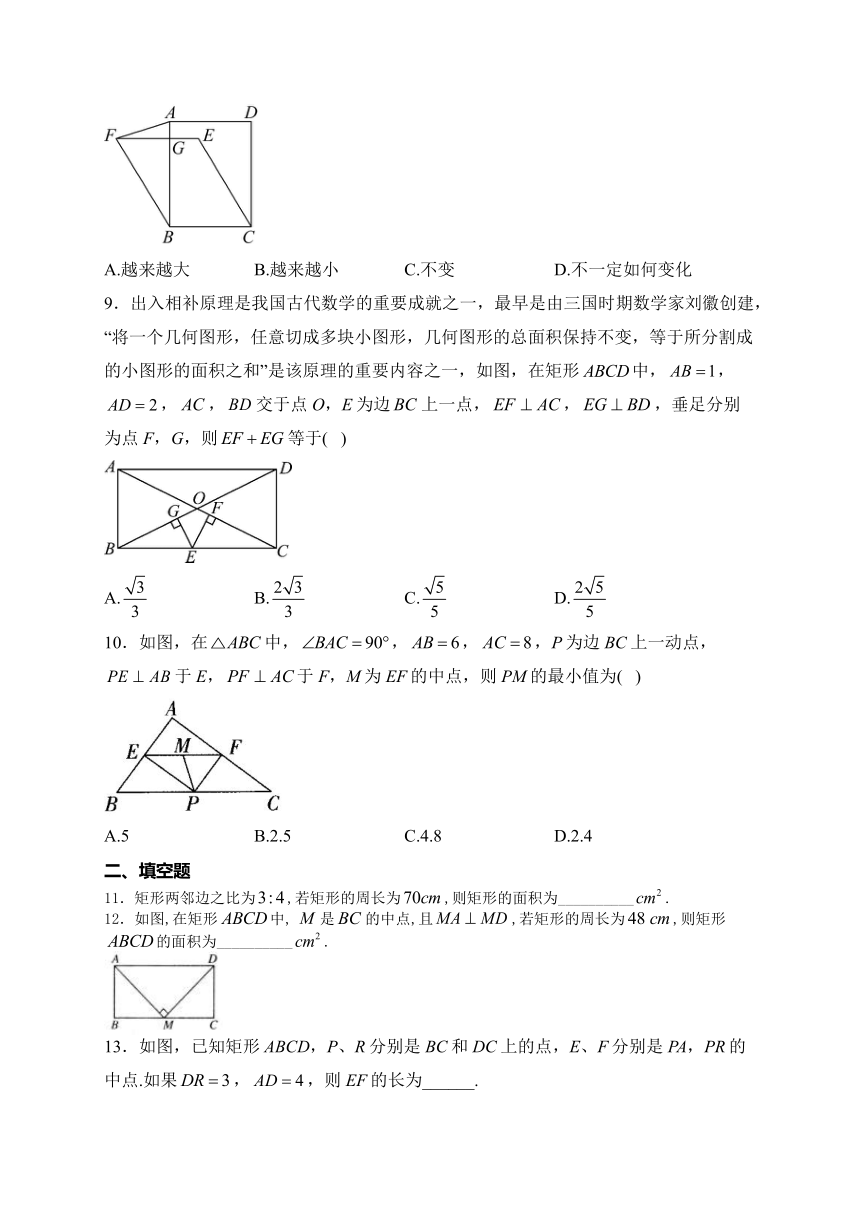
8.三角形具有稳定性,但是四边形不具有.水平向左推动如图所示的矩形,得到新的四边形(点E在矩形的内部),直线交于点G,连接,在向左推动的过程中的面积变化情况是( )
A.越来越大 B.越来越小 C.不变 D.不一定如何变化
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建,“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形中,,,,交于点O,E为边上一点,,,垂足分别为点F,G,则等于( )
A. B. C. D.
10.如图,在中,,,,P为边BC上一动点,于E,于F,M为EF的中点,则PM的最小值为( )
A.5 B.2.5 C.4.8 D.2.4
二、填空题
11.矩形两邻边之比为,若矩形的周长为,则矩形的面积为__________.
12.如图,在矩形中, 是的中点,且,若矩形的周长为,则矩形的面积为__________.
13.如图,已知矩形ABCD,P、R分别是BC和DC上的点,E、F分别是PA,PR的中点.如果,,则EF的长为______.
14.在坐标平面内,A,B两点的坐标分别是,,点C在y轴上,点D在坐标平面内,以A,B,C,D为顶点的四边形是矩形,则点D的坐标为__________.
15.如图是一张长方形纸片ABCD,已知,,E为AB上一点,,现要剪下一张等腰三角形纸片(),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是_____________.
三、解答题
16.如图,在中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且,连接CF.
(1)求证:D是BC的中点;
(2)如果,试猜测四边形ADCF的形状,并证明你的结论.
17.如图,平行四边形ABCD的四个内角的平分线分别相交于点E,F,G,H,求证:四边形EFGH是矩形.
18.已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:;
(2)若,,判断四边形ACDF的形状,并证明你的结论.
19.如图,在中,点M为AC的中点,过点D作,延长CB到点E使,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若,,,求EM的长.
20.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且.
(1)求证:四边形AECF是平行四边形;
(2)当,,时,若四边形AECF是矩形,求BE的长.
21.如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:;
(2)若,,求BC的长.
22.如图,在中,O是AC边上一点,过点O作BC的平行线,交的平分线于点E,交外角的平分线于点F.
(1)求证:;
(2)连接AE,AF,当点O沿AC运动时,四边形AECF是否能成为一个矩形 此时,点O在什么位置 说明理由.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在矩形中,O是对角线,的交点,于点E,若,,则的长为( )
A. B. C. D.
2.如图,四边形ABCD的对角线相交于点O,且互相平分.若添加下列条件,不能判定四边形ABCD为矩形的是( )
A. B.
C. D.
3.如图,在矩形ABCD中,点E在AD上,且EC平分,,,则DE的长为( )
A. B. C. D.
4.如图,将矩形纸片沿直线折叠,使点C落在边的中点处,点B落在点处,其中,,则的长为( )
A. B.4 C.4.5 D.5
5.如图,矩形中,,,点F为边上一点,连接,若线段绕点F顺时针旋转后,点D恰好落在边上的点E处,则的长度为( )
A.2 B.1 C.3 D.1.5
6.如图,矩形中,对角线,相交于点O,点E,F,G分别是,,的中点,且,则的长为( )
A.4 B.3 C.2 D.1
7.如图,在矩形中,、相交于点O,平分交于点E,若,则的度数为( )
A. B. C. D.
8.三角形具有稳定性,但是四边形不具有.水平向左推动如图所示的矩形,得到新的四边形(点E在矩形的内部),直线交于点G,连接,在向左推动的过程中的面积变化情况是( )
A.越来越大 B.越来越小 C.不变 D.不一定如何变化
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建,“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形中,,,,交于点O,E为边上一点,,,垂足分别为点F,G,则等于( )
A. B. C. D.
10.如图,在中,,,,P为边BC上一动点,于E,于F,M为EF的中点,则PM的最小值为( )
A.5 B.2.5 C.4.8 D.2.4
二、填空题
11.矩形两邻边之比为,若矩形的周长为,则矩形的面积为__________.
12.如图,在矩形中, 是的中点,且,若矩形的周长为,则矩形的面积为__________.
13.如图,已知矩形ABCD,P、R分别是BC和DC上的点,E、F分别是PA,PR的中点.如果,,则EF的长为______.
14.在坐标平面内,A,B两点的坐标分别是,,点C在y轴上,点D在坐标平面内,以A,B,C,D为顶点的四边形是矩形,则点D的坐标为__________.
15.如图是一张长方形纸片ABCD,已知,,E为AB上一点,,现要剪下一张等腰三角形纸片(),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是_____________.
三、解答题
16.如图,在中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且,连接CF.
(1)求证:D是BC的中点;
(2)如果,试猜测四边形ADCF的形状,并证明你的结论.
17.如图,平行四边形ABCD的四个内角的平分线分别相交于点E,F,G,H,求证:四边形EFGH是矩形.
18.已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:;
(2)若,,判断四边形ACDF的形状,并证明你的结论.
19.如图,在中,点M为AC的中点,过点D作,延长CB到点E使,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若,,,求EM的长.
20.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且.
(1)求证:四边形AECF是平行四边形;
(2)当,,时,若四边形AECF是矩形,求BE的长.
21.如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:;
(2)若,,求BC的长.
22.如图,在中,O是AC边上一点,过点O作BC的平行线,交的平分线于点E,交外角的平分线于点F.
(1)求证:;
(2)连接AE,AF,当点O沿AC运动时,四边形AECF是否能成为一个矩形 此时,点O在什么位置 说明理由.
