2024年湖南省长沙市长郡集团九年级毕业会考模拟练习数学试卷(一)(无答案)
文档属性
| 名称 | 2024年湖南省长沙市长郡集团九年级毕业会考模拟练习数学试卷(一)(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-17 22:39:31 | ||
图片预览


文档简介
长郡2024年春季九年级毕业会考模拟练习卷(一)
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共25个小题,考试时量120分钟,满分120分.
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分)
1.的倒数是( )
A.2023 B. C. D.
2.2022年10月12日,“天宫课堂”第三课在中国空间站开讲,3名航天员演示了在微重力环境下毛细效应实验、水球变“懒”实验等,相应视频在某短视频平台的点赞量达到150万次,数据150万用科学记数法表示为( )
A. B. C. D.
3.计算的结果是( )
A.2 B. C.0 D.
4.在以下节水、节能、回收、绿色食品四个标志中,是轴对称图形的是( )
A. B. C. D.
5.以下列数值为长度的各组线段中,能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
6.为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )
A.此次调查属于全面调查 B.样本容量是300
C.2000名学生是总体 D.被抽取的每一名学生称为个体
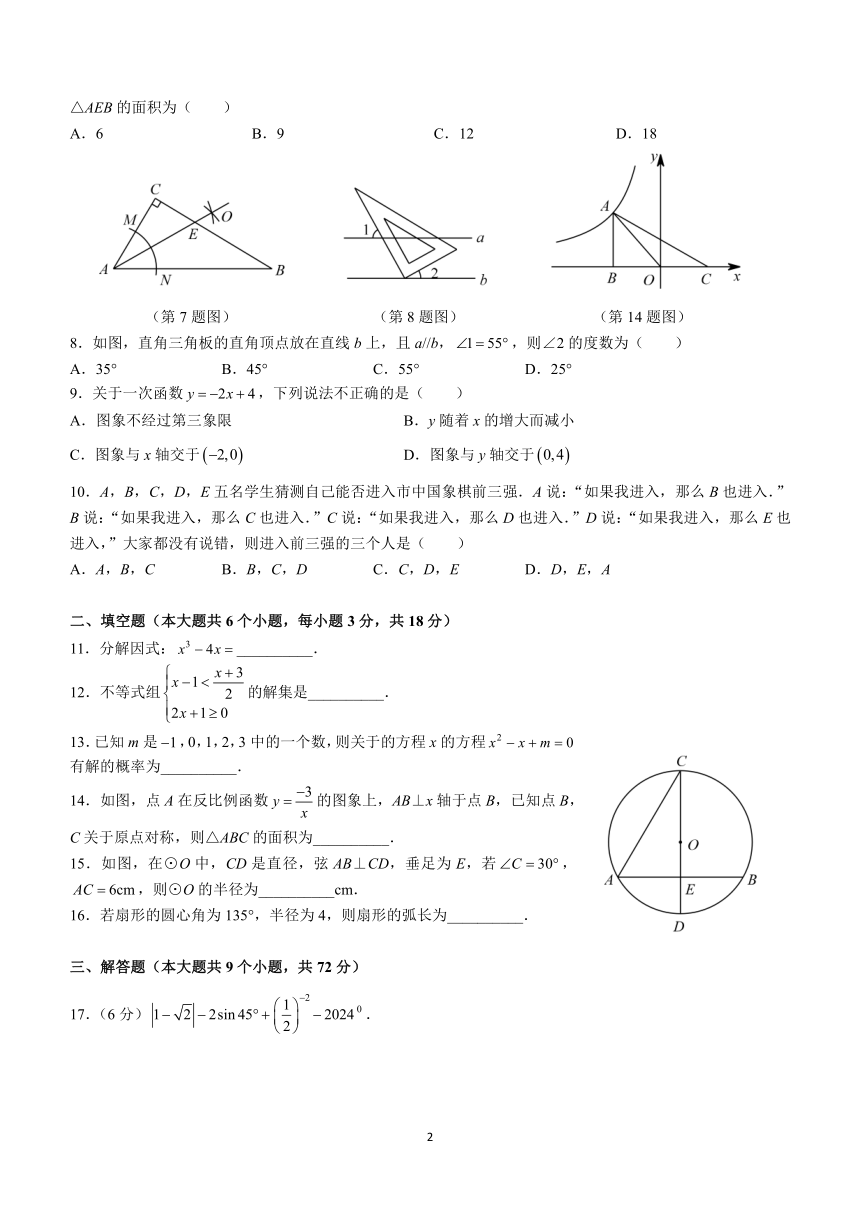
7.如图,在△ABC中,,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知,,△AEB的面积为( )
A.6 B.9 C.12 D.18
(第7题图) (第8题图) (第14题图)
8.如图,直角三角板的直角顶点放在直线b上,且a//b,,则∠2的度数为( )
A.35° B.45° C.55° D.25°
9.关于一次函数,下列说法不正确的是( )
A.图象不经过第三象限 B.y随着x的增大而减小
C.图象与x轴交于 D.图象与y轴交于
10.A,B,C,D,E五名学生猜测自己能否进入市中国象棋前三强.A说:“如果我进入,那么B也进入.”B说:“如果我进入,那么C也进入.”C说:“如果我进入,那么D也进入.”D说:“如果我进入,那么E也进入,”大家都没有说错,则进入前三强的三个人是( )
A.A,B,C B.B,C,D C.C,D,E D.D,E,A
二、填空题(本大题共6个小题,每小题3分,共18分)
11.分解因式:__________.
12.不等式组的解集是__________.
13.已知m是,0,1,2,3中的一个数,则关于的方程x的方程有解的概率为__________.
14.如图,点A在反比例函数的图象上,AB⊥x轴于点B,已知点B,C关于原点对称,则△ABC的面积为__________.
15.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若,,则⊙O的半径为__________cm.
16.若扇形的圆心角为135°,半径为4,则扇形的弧长为__________.
三、解答题(本大题共9个小题,共72分)
17.(6分).
18.(6分)先化简,再求值:,其中,.
19.(6分)某校数学社团开展“探索生活中的数学”研学活动,小亮想测量某大厦楼顶上的一个广告牌CD的高度,从与大厦BC相距30m的A处观测广告牌顶部D的仰角,观测广告牌底部C的仰角为,如图所示.
(1)求大厦BC的高度;(结果精确到)
(2)求广告牌CD的高度.(结果取整数)
(参考数据:,,,)
20.(8分)打造书香文化,培养阅读习惯,某校举行了以“礼、才、恩”为主题的读书活动,开展“我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:政史类,B:文学类,C:科技类,D:艺术类,E:其他类).柳老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为_______名,并补全条形统计图;
(2)在扇形统计图中,C“科技类”所对应的圆心角度数是_______度;
(3)若该校有3000名学生,请你估计最喜欢阅读文学类书籍的学生人数;
(4)甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
21.(8分)如图,点C在线段BD上,AB⊥BD,ED⊥BD,AC⊥CE,.
(1)求证:△ABC≌△CDE;
(2)已知,,求△ACE的面积.
22.(9分)为了调动学生学习数学的兴趣,某校八年级举行了数学计算题比赛,为表彰获奖的选手,年级组准备在学校对面的晨光文具店购买A,B两种文具作为奖品.已知A文具的单价比B文具的单价贵8元,且用720元购买A文具的数量与用480元购买B文具的数量相同.
(1)求A,B两种文具的单价;
(2)若年级组需要购买A,B两种文具共100件,且购买这两种文具的总费用不超过2080元,则年级组至少购买B种文具多少件?
23.(9分)在Rt△ABC中,,D是BC的中点,E是AD的中点,过点A作AF//BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若,,求CF的长.
24.在平面直角坐标系中有且只有一个交点的两个函数称为“亲密函数”,这个唯一的交点称为他们的“密接点”.例如:与有且只有一个交点,则称这两个函数为“亲密函数”,点称为他们的“密接点”.
(1)判断下列几组函数,是“亲密函数”的在( )内记“√”,不是“亲密函数”的在( )内记“×”:
①与;( )
②与;( )
③与.( )
(2)一次函数与反比例函数(其中k,b为常数,是“亲密函数”,且他们的“密接点”P到原点的距离等于3,求b的值.
(3)两条直线l1与l2都是二次函数的“亲密函数”,且“密接点”分别为M,N.记直线l1与l2的交点的纵坐标为m,直线MN与y轴的交点的纵坐标为n.试判断m与n的关系,并证明你的判断.
25.(10分)如图,四边形ABCD内接于⊙O,对角线AC,BD相交于点M,.
(1)求证:.
(2)当时,记,记.
①当时,求t的值;
②求t的最大值.
(3)当AD为直径时,连接OB交AC于点E,满足以下条件:①;②;③(m,n均为正整数);求⊙O的半径r的值.
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共25个小题,考试时量120分钟,满分120分.
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分)
1.的倒数是( )
A.2023 B. C. D.
2.2022年10月12日,“天宫课堂”第三课在中国空间站开讲,3名航天员演示了在微重力环境下毛细效应实验、水球变“懒”实验等,相应视频在某短视频平台的点赞量达到150万次,数据150万用科学记数法表示为( )
A. B. C. D.
3.计算的结果是( )
A.2 B. C.0 D.
4.在以下节水、节能、回收、绿色食品四个标志中,是轴对称图形的是( )
A. B. C. D.
5.以下列数值为长度的各组线段中,能组成三角形的是( )
A.2,4,7 B.3,3,6 C.5,8,2 D.4,5,6
6.为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )
A.此次调查属于全面调查 B.样本容量是300
C.2000名学生是总体 D.被抽取的每一名学生称为个体
7.如图,在△ABC中,,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知,,△AEB的面积为( )
A.6 B.9 C.12 D.18
(第7题图) (第8题图) (第14题图)
8.如图,直角三角板的直角顶点放在直线b上,且a//b,,则∠2的度数为( )
A.35° B.45° C.55° D.25°
9.关于一次函数,下列说法不正确的是( )
A.图象不经过第三象限 B.y随着x的增大而减小
C.图象与x轴交于 D.图象与y轴交于
10.A,B,C,D,E五名学生猜测自己能否进入市中国象棋前三强.A说:“如果我进入,那么B也进入.”B说:“如果我进入,那么C也进入.”C说:“如果我进入,那么D也进入.”D说:“如果我进入,那么E也进入,”大家都没有说错,则进入前三强的三个人是( )
A.A,B,C B.B,C,D C.C,D,E D.D,E,A
二、填空题(本大题共6个小题,每小题3分,共18分)
11.分解因式:__________.
12.不等式组的解集是__________.
13.已知m是,0,1,2,3中的一个数,则关于的方程x的方程有解的概率为__________.
14.如图,点A在反比例函数的图象上,AB⊥x轴于点B,已知点B,C关于原点对称,则△ABC的面积为__________.
15.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若,,则⊙O的半径为__________cm.
16.若扇形的圆心角为135°,半径为4,则扇形的弧长为__________.
三、解答题(本大题共9个小题,共72分)
17.(6分).
18.(6分)先化简,再求值:,其中,.
19.(6分)某校数学社团开展“探索生活中的数学”研学活动,小亮想测量某大厦楼顶上的一个广告牌CD的高度,从与大厦BC相距30m的A处观测广告牌顶部D的仰角,观测广告牌底部C的仰角为,如图所示.
(1)求大厦BC的高度;(结果精确到)
(2)求广告牌CD的高度.(结果取整数)
(参考数据:,,,)
20.(8分)打造书香文化,培养阅读习惯,某校举行了以“礼、才、恩”为主题的读书活动,开展“我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:政史类,B:文学类,C:科技类,D:艺术类,E:其他类).柳老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为_______名,并补全条形统计图;
(2)在扇形统计图中,C“科技类”所对应的圆心角度数是_______度;
(3)若该校有3000名学生,请你估计最喜欢阅读文学类书籍的学生人数;
(4)甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.
21.(8分)如图,点C在线段BD上,AB⊥BD,ED⊥BD,AC⊥CE,.
(1)求证:△ABC≌△CDE;
(2)已知,,求△ACE的面积.
22.(9分)为了调动学生学习数学的兴趣,某校八年级举行了数学计算题比赛,为表彰获奖的选手,年级组准备在学校对面的晨光文具店购买A,B两种文具作为奖品.已知A文具的单价比B文具的单价贵8元,且用720元购买A文具的数量与用480元购买B文具的数量相同.
(1)求A,B两种文具的单价;
(2)若年级组需要购买A,B两种文具共100件,且购买这两种文具的总费用不超过2080元,则年级组至少购买B种文具多少件?
23.(9分)在Rt△ABC中,,D是BC的中点,E是AD的中点,过点A作AF//BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若,,求CF的长.
24.在平面直角坐标系中有且只有一个交点的两个函数称为“亲密函数”,这个唯一的交点称为他们的“密接点”.例如:与有且只有一个交点,则称这两个函数为“亲密函数”,点称为他们的“密接点”.
(1)判断下列几组函数,是“亲密函数”的在( )内记“√”,不是“亲密函数”的在( )内记“×”:
①与;( )
②与;( )
③与.( )
(2)一次函数与反比例函数(其中k,b为常数,是“亲密函数”,且他们的“密接点”P到原点的距离等于3,求b的值.
(3)两条直线l1与l2都是二次函数的“亲密函数”,且“密接点”分别为M,N.记直线l1与l2的交点的纵坐标为m,直线MN与y轴的交点的纵坐标为n.试判断m与n的关系,并证明你的判断.
25.(10分)如图,四边形ABCD内接于⊙O,对角线AC,BD相交于点M,.
(1)求证:.
(2)当时,记,记.
①当时,求t的值;
②求t的最大值.
(3)当AD为直径时,连接OB交AC于点E,满足以下条件:①;②;③(m,n均为正整数);求⊙O的半径r的值.
同课章节目录
