第18章《勾股定理》单元测试卷(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
沪科版八下第18章勾股定理单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.在平面直角坐标系中,点到原点的距离是( )
A.1 B. C.2 D.
2.如图,在△ABC中,∠A是钝角,若AB=1,AC=3,则BC的长度可能是( )
A.π﹣1 B.3 C. D.
3.线段在平面直角坐标系中的位置如图所示,,,线段的长为( )
A.5 B. C.4 D.3
4.在下列四组数中,属于勾股数的是( )
A. B. C.3,5,7 D.5,12,13
5.在中,,两直角边 ,,在三角形内有一点到各边的距离相等,则这个距离是( )
A.1 B.2 C.3 D.4
6.李晨想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成?( )
A.2,3,4 B.3,4,5 C.4,5,6 D.1,1,2
7.如图,四边形是长方形地面,长,宽,中间竖有一堵砖墙高,一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它至少要走( )
A. B. C. D.
8.如图,将长为的橡皮筋放置在水平面上,固定两端A和B,然后把中点C垂直向上拉升至点D,则橡皮筋被拉长了( )
A. B. C. D.
9.两艘轮船从同一港口同时出发,甲船时速海里,乙船时速海里,两个小时后,两船相距海里,已知甲船的航向为北偏东,则乙船的航向为( )
A.南偏东 B.北偏西 C.南偏东或北偏西 D.无法确定
10.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为129.则小正方形的边长为( )
A.7 B.8 C.9 D.10
11.如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值等于 ( )
A.+3 B.2-2 C.2- D.2+3
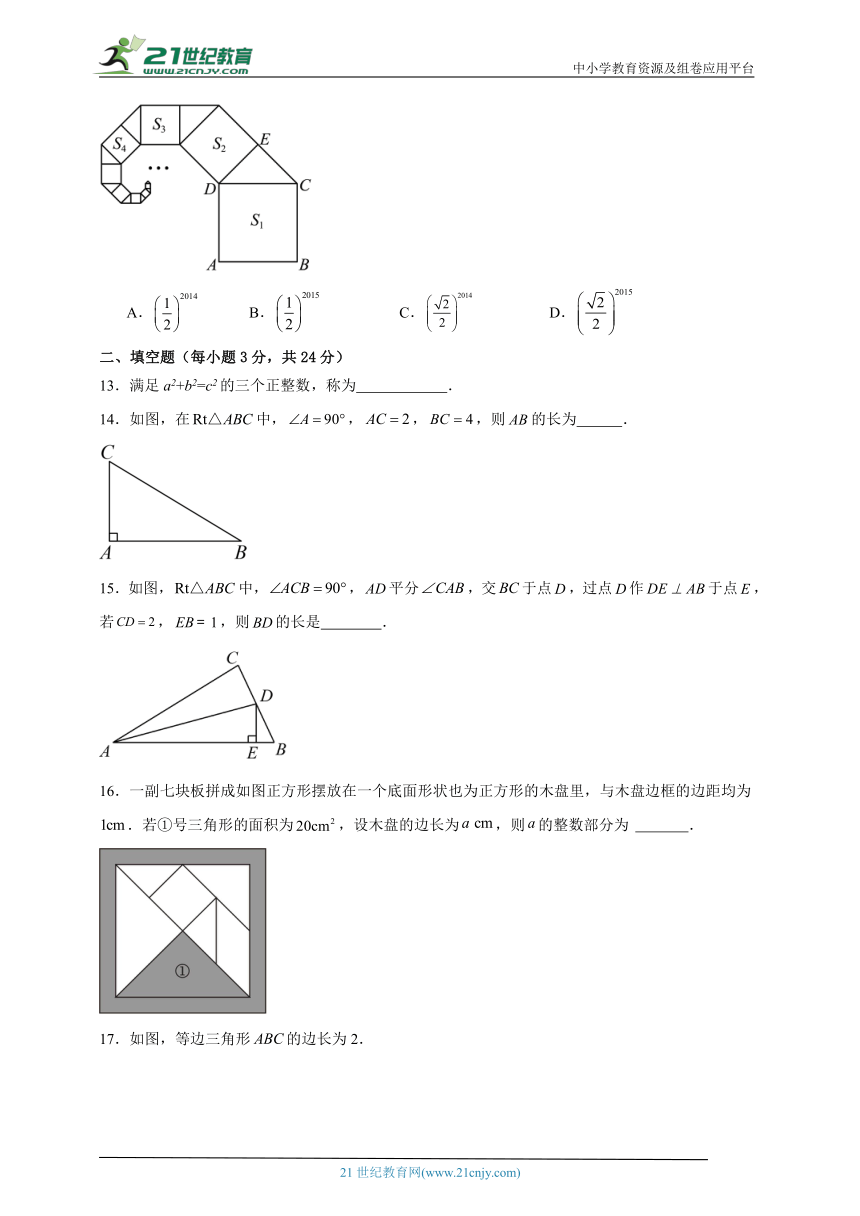
12.如图,正方形ABCD的面积S1=2,以CD为斜边,向外作等腰直角三角形,再以该等腰直角三角形的一条直角边为边,向外作正方形,其面积标记为S2,………按照此规律继续下去,则S2016的值为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.满足a2+b2=c2的三个正整数,称为 .
14.如图,在中,,,,则的长为 .
15.如图,中,,平分,交于点,过点作于点,若,,则的长是 .
16.一副七块板拼成如图正方形摆放在一个底面形状也为正方形的木盘里,与木盘边框的边距均为.若①号三角形的面积为,设木盘的边长为,则的整数部分为 .
17.如图,等边三角形的边长为2.
(1)的面积是 .
(2)分别以点A,C为圆心,m为半径作弧,两弧交于点D,连接.若的长为,则m的值为 .
18.已知平面直角坐标系内一点,O为坐标原点,点C是y轴上一点,且是等腰三角形,则点C的坐标是 .
19.如图,将放在正方形网格图中(图中每个小正方形的边长均为),点,, 恰好在网格图中的格点上,那么中边上的高是 .
20.如图,在直角梯形中,,点在上,且是以为底的等腰直角三角形,若,则 , .
三、解答题(共60分)
21.(8分)已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根.
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的面积.
22.(8分)如图,在中,于点,于点,交于点.
(1)求证:.
(2)若,求的长.
23.(8分)如图,在等腰三角形中,,,点D是中点,点E是的中点,连接.
(1)求证:;
(2)求的面积.
24.(8分)做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做一个边长为c的正方形,把它们按如图的方式拼成正方形,请用这个图证明勾股定理.
25.(10分)在等腰直角中,,是线段上一点(与点不重合),连接,延长至点.使得,过点作于点,交于点.
(1)求证:.
(2)求证:.
(3)用等式表示线段与之间的数量关系,并证明.
26.(8分)如图,在△ABC中,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E.
(1)求证:BD=CE;
(2)当AB=5,CE=2时,求BC的长
27.(10分)知,点B在射线上,点A是射线上的一个动点(不与点C重合).点B关于的对称点为点D,连接和,点F在直线上,且满足.小明在探究图形运动的过程中发现:始终成立.
(1)如图1,当时.
①求证:;
②用等式表示线段、与之间的数量关系,并证明;
(2)当时,直接用等式表示线段、与之间的数量关系是____________.
第18章勾股定理单元测试参考答案
1.D[提示:在平面直角坐标系中,点到原点的距离是
故选:D]
2.C[提示:根据三角形三边关系,第三边小于AB+AC=4,
当∠A为直角时,AB,AC分别是两直角边,
则第三边即斜边的长度为BC=,
故<BC<4,
只有C选项符合题意,故选C.]
3.A[提示:∵,,
∴点A和点B的水平距离为4,竖直距离为3,
∴.
故选:A.]
4.D[提示:A、不是整数,故不是勾股数,不符合题意;
B、1,,不是整数,故不是勾股数,不符合题意;
C、,故不是勾股数,不符合题意;
D、,故是勾股数,符合题意;
故选:D.]
5.B[提示:如图,
连接PA、PB、PC,
设点到各边的距离为x,
∵∠C=90°,两直角边AC=5,BC=12,
∴AB=,
由题意得,
解得,x=2,
故选:B.]
6.B[提示:A、,不能构成直角三角形,故此选项错误;
B、,能构成直角三角形,故此选项正确
C、,不能构成直角三角形,故此选项错误
D、,不能构成直角三角形,故此选项错误
故选:B]
7.A[提示:如图,将墙展开,长方形长度增加,则,连接,
∵四边形是长方形,
∴,
∴,
,
∴蚂蚱从点爬到点,它必须翻过中间那堵墙,它至少要走.
故选:A.]
8.A[提示:由题意可得,
,,
根据勾股定理可得,
,
∴橡皮筋被拉长了:.,
故选:A.]
9.C[提示:由题意得,海里,海里,,
∵,,
∴,
∴点三点共线,
∵,
∴,
∵,
∴,
∴乙船的航向为南偏东或北偏西,
故选:.]
10.C[提示:由题意,中间小正方形的边长为,,,
∵,
∴,
∵,
∴,
故选:C.]
11.B[解:过E作EM⊥DC于M.∵EM=AB, EG =BF,∴△EMG≌△BAF,∴∠MEG=∠ABF.∵∠MEG+∠GEB=90°,∴∠ABF+∠BEG=90°,∴∠EIB=90°.以BE为直径作半⊙O,连结OD,则OD≤OI+ID(两边之和大于第三边),当O、I、D三点共线时取等号.∵OI=2,OD==.∴DI≥OD-OI=.故选B.
]
12.A[解:∵S1=2,则正方形ABCD的边长为,
,
,
,
……
,
故选:A.]
13.勾股数
14.[提示:在直角中,
,
为斜边,
∴,
∵,,
∴,
故答案为:.]
15.[提示:平分,,,
,
在中,根据勾股定理得,
.故答案为:]
16.[提示:如图,
由题意得①是等腰直角三角形,面积为,
∴,
∴(),
∵,
∴由勾股定理得(),
∴(),
即(),
∵,
即,
∴,
∴的整数部分为,
即的整数部分为,
故答案为:.]
17. 或2/2或[提示:(1)过点B作于点E,
∵等边三角形的边长为2,
∴,
∴,
∴的面积是,
故答案为:.
(2)根据作图,得到点D一定在线段的垂直平分线上,
故直线是线段的垂直平分线,
当点D位于右侧时,
∵等边三角形的边长为2,
∴,
∴,
∵,
∴,
∴,
∴;
当点D位于左侧时,
∵等边三角形的边长为2,
∴,
∴,
∵,
∴,
∴,
∴;故答案为:或2.]
18.(0, )或(0, )或(0,4)或[提示:点,
,
是等腰三角形,
①若,
或,
②若时,,
,
③若时,点在的垂直平分线上,且D点在线段的中点,如图,
设,则,
由勾股定理得,
则,
解得,
∴;
综上所述,点的坐标是或或或,
故答案为:或或或.]
19.[提示:根据图形可得:,,
∴,
∴是直角三角形,且,
设中的高是x,
则,
∴,
解得,
故答案为:.]
20. 6 [提示:过点E作EF⊥AB于F.
∵AD∥BC,∠DAB=∠ABC=90°,
∴EF∥BC∥AD.
又∵△ABE是以AB为底边的等腰直角三角形,
∴AE=EB,∠ABE=∠BAE=45°,
∴F为AB的中点,
∴AF=FE=FB.
∴EF为梯形的中位线.
∵AD=2cm,BC=4cm,
∴EF=(BC+AD)=3cm.
∴AB=AF+FB=3+3=6(cm);
过点A作AG∥CD交BC于点G,
∵AD∥BC,∴四边形ADCG为平行四边形,∴AG=CD,CG=AD=2cm.
∴BG=BC-CG=2cm,
在Rt△ABG中,AG==(cm).
∴CD=cm.
故答案为:6;.]
21.(1)证明:,
其中:,,,
∴,
∴在实数范围内,m无论取何值,,
即,
∴关于x的方程恒有两个不相等的实数根;
(2)解:根据题意得:将代入方程可得:
,
解得,
∴方程为,
解得:或,
∴方程的另一个根为;
①当该直角三角形的两直角边是1、3时,
该直角三角形的面积为:;
②当该直角三角形的直角边和斜边分别是1、3时,
由勾股定理得该直角三角形的另一直角边为,
则该直角三角形的面积为;
综上可得,该直角三角形的面积为或.
22.(1)证明:∵,
∴,,
∵,
∴,
在与中,
,
∴.
(2)解:∵,
∴,,
∴,
∴,
∴,即.
23.(1)证明:连接,如图所示,
∵在中,,E是的中点,
∴,
∴是直角三角形,
又∵D是的中点
∴;
(2)解:∵E是的中点,,
∴,
在中,,,
∴,
∴;
24.证明:如图,,,,
∵,即
∴,
∴.
25.(1)∵∠ACB=90°,
∴∠CPH+∠PAC=90°.
∵QM⊥AP,
∴∠QHP=90°,
∴∠MQB+∠CPH=90°,
∴∠MQB=∠PAC;
(2)连接AQ,如图所示.
∵AC⊥QP,CQ=CP,
∴AQ=AP,
∴∠QAC=∠PAC.
∵∠QAM=∠QAC+∠BAC=∠PAC+45°,∠AMQ=∠MQB+∠B=∠PAC+45°,
∴∠QAM=∠AMQ,
∴AQ=QM.
∵AQ=AP,
∴AP=QM.
(3)MBCP.理由如下:
作ME⊥QB与E,
在△APC和△QME中,
∵∠MQE=∠PAC,∠ACP=∠QEM=90°,AP=QM,
∴△APC≌△QME(AAS),
∴PC=ME.
∵△MEB是等腰直角三角形,
∴BE=ME.
∵,
∴MBME,
∴MBCP.
26.证明:(1)∵AB=AC
∴∠ABC=∠ACB,且BC=BC,∠BDC=∠BEC
∴△BDC≌△CEB(AAS)
∴BD=CE,
(2)∵AB=AC=5,CE=2
∴AE=3
∴BE= =4
∴BC==2
27.(1)①证明:∵B、D关于对称,
∴,,
∵公共,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
②,证明如下:
如图,延长到E,使,连接,
∵,,
∴,
∵,,
∴,
∴,
∴,,
即是等腰直角三角形,
由勾股定理得,
即,
∵,
∴,
即、与之间的数量关系为;
;
(2)如图,在线段上取,连接,
∵,
∴,,
∵,
∴,,
∴,
∴,
∴,
∴,
∴,
即是等腰直角三角形,
由勾股定理得,
即,
∵,
∴,
即、与之间的数量关系为;
故答案为:
;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版八下第18章勾股定理单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.在平面直角坐标系中,点到原点的距离是( )
A.1 B. C.2 D.
2.如图,在△ABC中,∠A是钝角,若AB=1,AC=3,则BC的长度可能是( )
A.π﹣1 B.3 C. D.
3.线段在平面直角坐标系中的位置如图所示,,,线段的长为( )
A.5 B. C.4 D.3
4.在下列四组数中,属于勾股数的是( )
A. B. C.3,5,7 D.5,12,13
5.在中,,两直角边 ,,在三角形内有一点到各边的距离相等,则这个距离是( )
A.1 B.2 C.3 D.4
6.李晨想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成?( )
A.2,3,4 B.3,4,5 C.4,5,6 D.1,1,2
7.如图,四边形是长方形地面,长,宽,中间竖有一堵砖墙高,一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它至少要走( )
A. B. C. D.
8.如图,将长为的橡皮筋放置在水平面上,固定两端A和B,然后把中点C垂直向上拉升至点D,则橡皮筋被拉长了( )
A. B. C. D.
9.两艘轮船从同一港口同时出发,甲船时速海里,乙船时速海里,两个小时后,两船相距海里,已知甲船的航向为北偏东,则乙船的航向为( )
A.南偏东 B.北偏西 C.南偏东或北偏西 D.无法确定
10.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为129.则小正方形的边长为( )
A.7 B.8 C.9 D.10
11.如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值等于 ( )
A.+3 B.2-2 C.2- D.2+3
12.如图,正方形ABCD的面积S1=2,以CD为斜边,向外作等腰直角三角形,再以该等腰直角三角形的一条直角边为边,向外作正方形,其面积标记为S2,………按照此规律继续下去,则S2016的值为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
13.满足a2+b2=c2的三个正整数,称为 .
14.如图,在中,,,,则的长为 .
15.如图,中,,平分,交于点,过点作于点,若,,则的长是 .
16.一副七块板拼成如图正方形摆放在一个底面形状也为正方形的木盘里,与木盘边框的边距均为.若①号三角形的面积为,设木盘的边长为,则的整数部分为 .
17.如图,等边三角形的边长为2.
(1)的面积是 .
(2)分别以点A,C为圆心,m为半径作弧,两弧交于点D,连接.若的长为,则m的值为 .
18.已知平面直角坐标系内一点,O为坐标原点,点C是y轴上一点,且是等腰三角形,则点C的坐标是 .
19.如图,将放在正方形网格图中(图中每个小正方形的边长均为),点,, 恰好在网格图中的格点上,那么中边上的高是 .
20.如图,在直角梯形中,,点在上,且是以为底的等腰直角三角形,若,则 , .
三、解答题(共60分)
21.(8分)已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根.
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的面积.
22.(8分)如图,在中,于点,于点,交于点.
(1)求证:.
(2)若,求的长.
23.(8分)如图,在等腰三角形中,,,点D是中点,点E是的中点,连接.
(1)求证:;
(2)求的面积.
24.(8分)做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做一个边长为c的正方形,把它们按如图的方式拼成正方形,请用这个图证明勾股定理.
25.(10分)在等腰直角中,,是线段上一点(与点不重合),连接,延长至点.使得,过点作于点,交于点.
(1)求证:.
(2)求证:.
(3)用等式表示线段与之间的数量关系,并证明.
26.(8分)如图,在△ABC中,AB=AC,CD⊥AB,BE⊥AC,垂足分别为点D,E.
(1)求证:BD=CE;
(2)当AB=5,CE=2时,求BC的长
27.(10分)知,点B在射线上,点A是射线上的一个动点(不与点C重合).点B关于的对称点为点D,连接和,点F在直线上,且满足.小明在探究图形运动的过程中发现:始终成立.
(1)如图1,当时.
①求证:;
②用等式表示线段、与之间的数量关系,并证明;
(2)当时,直接用等式表示线段、与之间的数量关系是____________.
第18章勾股定理单元测试参考答案
1.D[提示:在平面直角坐标系中,点到原点的距离是
故选:D]
2.C[提示:根据三角形三边关系,第三边小于AB+AC=4,
当∠A为直角时,AB,AC分别是两直角边,
则第三边即斜边的长度为BC=,
故<BC<4,
只有C选项符合题意,故选C.]
3.A[提示:∵,,
∴点A和点B的水平距离为4,竖直距离为3,
∴.
故选:A.]
4.D[提示:A、不是整数,故不是勾股数,不符合题意;
B、1,,不是整数,故不是勾股数,不符合题意;
C、,故不是勾股数,不符合题意;
D、,故是勾股数,符合题意;
故选:D.]
5.B[提示:如图,
连接PA、PB、PC,
设点到各边的距离为x,
∵∠C=90°,两直角边AC=5,BC=12,
∴AB=,
由题意得,
解得,x=2,
故选:B.]
6.B[提示:A、,不能构成直角三角形,故此选项错误;
B、,能构成直角三角形,故此选项正确
C、,不能构成直角三角形,故此选项错误
D、,不能构成直角三角形,故此选项错误
故选:B]
7.A[提示:如图,将墙展开,长方形长度增加,则,连接,
∵四边形是长方形,
∴,
∴,
,
∴蚂蚱从点爬到点,它必须翻过中间那堵墙,它至少要走.
故选:A.]
8.A[提示:由题意可得,
,,
根据勾股定理可得,
,
∴橡皮筋被拉长了:.,
故选:A.]
9.C[提示:由题意得,海里,海里,,
∵,,
∴,
∴点三点共线,
∵,
∴,
∵,
∴,
∴乙船的航向为南偏东或北偏西,
故选:.]
10.C[提示:由题意,中间小正方形的边长为,,,
∵,
∴,
∵,
∴,
故选:C.]
11.B[解:过E作EM⊥DC于M.∵EM=AB, EG =BF,∴△EMG≌△BAF,∴∠MEG=∠ABF.∵∠MEG+∠GEB=90°,∴∠ABF+∠BEG=90°,∴∠EIB=90°.以BE为直径作半⊙O,连结OD,则OD≤OI+ID(两边之和大于第三边),当O、I、D三点共线时取等号.∵OI=2,OD==.∴DI≥OD-OI=.故选B.
]
12.A[解:∵S1=2,则正方形ABCD的边长为,
,
,
,
……
,
故选:A.]
13.勾股数
14.[提示:在直角中,
,
为斜边,
∴,
∵,,
∴,
故答案为:.]
15.[提示:平分,,,
,
在中,根据勾股定理得,
.故答案为:]
16.[提示:如图,
由题意得①是等腰直角三角形,面积为,
∴,
∴(),
∵,
∴由勾股定理得(),
∴(),
即(),
∵,
即,
∴,
∴的整数部分为,
即的整数部分为,
故答案为:.]
17. 或2/2或[提示:(1)过点B作于点E,
∵等边三角形的边长为2,
∴,
∴,
∴的面积是,
故答案为:.
(2)根据作图,得到点D一定在线段的垂直平分线上,
故直线是线段的垂直平分线,
当点D位于右侧时,
∵等边三角形的边长为2,
∴,
∴,
∵,
∴,
∴,
∴;
当点D位于左侧时,
∵等边三角形的边长为2,
∴,
∴,
∵,
∴,
∴,
∴;故答案为:或2.]
18.(0, )或(0, )或(0,4)或[提示:点,
,
是等腰三角形,
①若,
或,
②若时,,
,
③若时,点在的垂直平分线上,且D点在线段的中点,如图,
设,则,
由勾股定理得,
则,
解得,
∴;
综上所述,点的坐标是或或或,
故答案为:或或或.]
19.[提示:根据图形可得:,,
∴,
∴是直角三角形,且,
设中的高是x,
则,
∴,
解得,
故答案为:.]
20. 6 [提示:过点E作EF⊥AB于F.
∵AD∥BC,∠DAB=∠ABC=90°,
∴EF∥BC∥AD.
又∵△ABE是以AB为底边的等腰直角三角形,
∴AE=EB,∠ABE=∠BAE=45°,
∴F为AB的中点,
∴AF=FE=FB.
∴EF为梯形的中位线.
∵AD=2cm,BC=4cm,
∴EF=(BC+AD)=3cm.
∴AB=AF+FB=3+3=6(cm);
过点A作AG∥CD交BC于点G,
∵AD∥BC,∴四边形ADCG为平行四边形,∴AG=CD,CG=AD=2cm.
∴BG=BC-CG=2cm,
在Rt△ABG中,AG==(cm).
∴CD=cm.
故答案为:6;.]
21.(1)证明:,
其中:,,,
∴,
∴在实数范围内,m无论取何值,,
即,
∴关于x的方程恒有两个不相等的实数根;
(2)解:根据题意得:将代入方程可得:
,
解得,
∴方程为,
解得:或,
∴方程的另一个根为;
①当该直角三角形的两直角边是1、3时,
该直角三角形的面积为:;
②当该直角三角形的直角边和斜边分别是1、3时,
由勾股定理得该直角三角形的另一直角边为,
则该直角三角形的面积为;
综上可得,该直角三角形的面积为或.
22.(1)证明:∵,
∴,,
∵,
∴,
在与中,
,
∴.
(2)解:∵,
∴,,
∴,
∴,
∴,即.
23.(1)证明:连接,如图所示,
∵在中,,E是的中点,
∴,
∴是直角三角形,
又∵D是的中点
∴;
(2)解:∵E是的中点,,
∴,
在中,,,
∴,
∴;
24.证明:如图,,,,
∵,即
∴,
∴.
25.(1)∵∠ACB=90°,
∴∠CPH+∠PAC=90°.
∵QM⊥AP,
∴∠QHP=90°,
∴∠MQB+∠CPH=90°,
∴∠MQB=∠PAC;
(2)连接AQ,如图所示.
∵AC⊥QP,CQ=CP,
∴AQ=AP,
∴∠QAC=∠PAC.
∵∠QAM=∠QAC+∠BAC=∠PAC+45°,∠AMQ=∠MQB+∠B=∠PAC+45°,
∴∠QAM=∠AMQ,
∴AQ=QM.
∵AQ=AP,
∴AP=QM.
(3)MBCP.理由如下:
作ME⊥QB与E,
在△APC和△QME中,
∵∠MQE=∠PAC,∠ACP=∠QEM=90°,AP=QM,
∴△APC≌△QME(AAS),
∴PC=ME.
∵△MEB是等腰直角三角形,
∴BE=ME.
∵,
∴MBME,
∴MBCP.
26.证明:(1)∵AB=AC
∴∠ABC=∠ACB,且BC=BC,∠BDC=∠BEC
∴△BDC≌△CEB(AAS)
∴BD=CE,
(2)∵AB=AC=5,CE=2
∴AE=3
∴BE= =4
∴BC==2
27.(1)①证明:∵B、D关于对称,
∴,,
∵公共,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
②,证明如下:
如图,延长到E,使,连接,
∵,,
∴,
∵,,
∴,
∴,
∴,,
即是等腰直角三角形,
由勾股定理得,
即,
∵,
∴,
即、与之间的数量关系为;
;
(2)如图,在线段上取,连接,
∵,
∴,,
∵,
∴,,
∴,
∴,
∴,
∴,
∴,
即是等腰直角三角形,
由勾股定理得,
即,
∵,
∴,
即、与之间的数量关系为;
故答案为:
;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
