北师大版七年级数学下册第五章生活中的轴对称单元复习题(含解析)
文档属性
| 名称 | 北师大版七年级数学下册第五章生活中的轴对称单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 10:45:26 | ||
图片预览

文档简介
北师大版七年级数学下册第五章生活中的轴对称单元复习题
一、选择题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 ( )
A.30° B.50° C.90° D.100°
3.如图,在中,结合尺规作图的痕迹,已知,的周长为14cm,则的周长是( )
A.17cm B.18cm C.19cm D.20cm
4.如所示四个图案中,不是轴对称图形的是( )
A. B.
C. D.
5.如图,将一张长方形纸片沿 EF折叠后,使得点 A,B 分别落在点A',B'的位置,如果∠2=56°,那么∠1=( )
A.56° B.58° C.62° D.68°
6.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B.
C. D.
7.等腰三角形的两边长分别为4和9,则它的周长( )
A.17 B.22 C.17或22 D.21
8.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或120° D.30°或150°
9.如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个 B.8个 C.9个 D.10个
二、填空题
10.小明从镜子里看到对面电子钟的像如图所示,则实际时间是 .
11.如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN= °.
12.如图,在内有一点O到三个顶点的距离相等,连接.若,则的度数为 .
13.如图,在的正方形格纸中,有一个以格点为顶点的,请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
三、解答题
14.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
15.如图,在中,,点,分别在边,上,连接,且和关于直线对称.
(1)若,则的度数为 .
(2)若,,且的周长为36,求的周长.
16.已知等腰三角形的两边长a、b满足|a﹣4|+(b﹣9)2=0,求这个等腰三角形的周长.
17.如图,请你以y轴为对称轴画出所给图的另一半,若点A坐标为(﹣3,3),写出点A的对应点的坐标,并说明完成后的图形可能代表的含义.
18.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N.
(1)①若∠AOB=60°,则∠COD= °;
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .
19.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.
(1)求证:AB∥CD;
(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保持(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
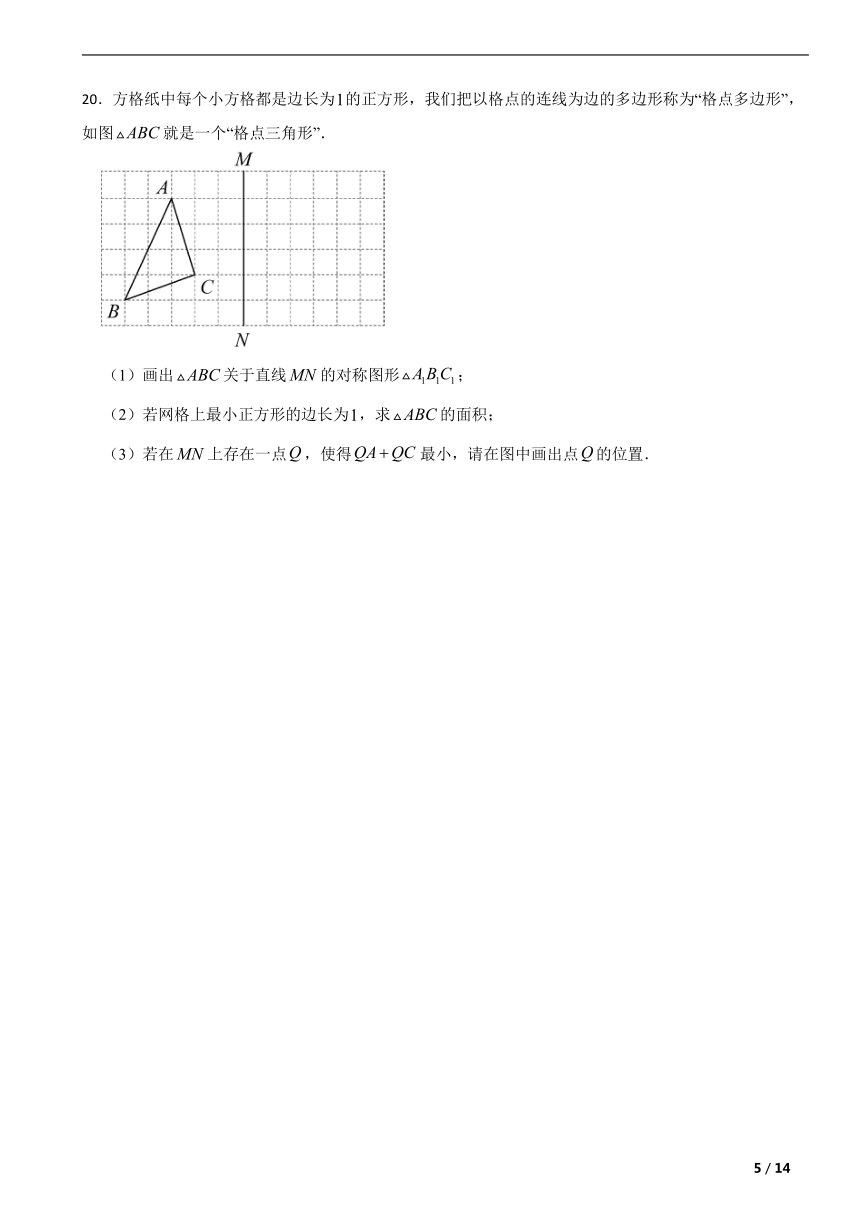
20.方格纸中每个小方格都是边长为的正方形,我们把以格点的连线为边的多边形称为“格点多边形”,如图就是一个“格点三角形”.
(1)画出关于直线的对称图形;
(2)若网格上最小正方形的边长为,求的面积;
(3)若在上存在一点,使得最小,请在图中画出点的位置.
答案解析部分
1.【答案】D
【解析】【解答】A、不是轴对称图形,故A不符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、是轴对称图形,故D符合题意.
故答案为:D.
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐一判断即可.
2.【答案】D
【解析】【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴∠A=∠A′=50°,∠C=∠C′=30°;∴∠B=180°﹣80°=100°.
故答案为:D.
【分析】根据轴对称的性质“成轴对称的两个图形全等”可求解.
3.【答案】B
【解析】【解答】解:由题意可知,DE垂直平分AC;
∴AE=EC,AC=2AD=4,
∴△ABC的周长=AB+BC+AC=AB+BE+AE+AC=14+4=18cm.
故答案为:B.
【分析】根据线段垂直平分线的性质,可得AE=EC,AC=2AD,再根据三角形的周长等于三边之和即可算出答案.
4.【答案】A
【解析】【解答】解:A、选项中的图形找不到一条直线,使直线两旁的部分能够完全重合,则不是轴对称图形,本项符合题意;
B、C、D、选项中可以找到一条直线,使直线两旁的部分能够完全重合,则是轴对称图形,本项不符合题意;
故答案为:A.
【分析】根据轴对称图形的定义:平面内,一个图形沿一条直线折叠 ,直线两旁的部分能够完全重合的图形,据此逐项分析即可.
5.【答案】C
6.【答案】C
【解析】【解答】解:利用轴对称的性质可得,C选项中AC+BC的长最小,
故答案为:C.
【分析】利用“将军饮马”的方法求解即可.
7.【答案】B
【解析】【解答】解:9为腰长时,三角形的周长为9+9+4=22,
9为底边长时,4+4<9,不能组成三角形,
故选:B.
【分析】分类讨论:9为腰长,9为底边长,根据三角形的周长公式,可得答案.
8.【答案】C
【解析】【解答】解:①如图所示:
∵BD⊥AC,
∴∠ADB = 90°,
∵等腰三角形一腰上的高与另一腰的夹角为30°,
∴∠ABD = 30°,
∴∠A = 180°-∠ADB-∠ABD=60°,
即顶角的度数为60°;
②如图所示:
∵BD⊥AC,
∴∠BDC = 90°,
∵等腰三角形一腰上的高与另一腰的夹角为30°,
∴∠ABD = 30°,
∴∠BAD =180°-∠BDC-∠ABD= 60°,
∴∠BAC =180°-∠BAD=120°,
即顶角的度数为120°;
综上所述:它的顶角度数为60°或120°,
故答案为:C.
【分析】根据等腰三角形的性质,结合图形,利用三角形的内角和计算求解即可。
9.【答案】D
【解析】【解答】如图,共有10种符合条件的添法,
故答案为:D.
【分析】根据轴对称的性质画出图形即可.
10.【答案】15:01
【解析】【解答】解:根据平面镜成像原理及轴对称图形的性质可知实际时间为15:01;
故答案为:15:01
【分析】利用平面镜成像原理及轴对称图形的性质可得到实际时间.
11.【答案】40
【解析】【解答】解:∵纸片沿MN折叠,MB与DN交于点K,∠1=70°,
∴∠1=∠BMN=70°.
∵四边形ABCD为矩形,
∴KN∥AM,
∴∠MKN=180°-2∠1=180°-140°=40°.
故答案为:40°.
【分析】根据折叠的性质可得:∠1=∠BMN=70°,由矩形的性质可得KN∥AM,然后根据平行线的性质进行计算.
12.【答案】
【解析】【解答】解:∵O到△ABC三个顶点距离相等,
∴OA=OB=OC,
∴∠CAO=∠ACO=55°,∠ABO=∠BAO=32°,
在△ABC中,∠OCB+∠OBC=180°-55°×2-25°×2=20°,
∴∠BOC=180°-20°=160°.
故答案为:160°.
【分析】由题意可知OA=OB=OC,由等边对等角得,∠CAO=∠ACO=55°,∠ABO=∠BAO=32°,再根据三角形内角和为180°,得出∠OCB+∠OBC=20°,就能求出∠BOC的度数.
13.【答案】5
【解析】【解答】解:与△ABC成轴对称且也以格点为顶点的三角形有5个,
分别为△BCD,△BFH,△ADC,△AEF,△CGH.
故答案为:5.
【分析】根据成轴对称的两个图形沿着对称轴折叠后能够重合画出所有与△ABC成抽对称的三角形,据此解答.
14.【答案】解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15
【解析】【分析】根据对称图形是全等的性质,则对应边相等,对应角也相等, 已知AB和DE的长度,∠D的度数,相应即可求出AD、BC的长度和∠B的度数。
15.【答案】(1)
(2)解:∵的周长为36,
∴,
∵,,
∴,解得,
∴.
∵和关于直线对称,
∴,
∴的周长
【解析】【解答】解:(1)在△ABC中,∠C=90°,∠B=40°,
∴∠CAB=90°-∠B=90°-40°=50°,
∵△AMN和△BMN关于直线MN对称,
∴ ∠NAB=∠B=40°,
∴ ∠CAN=∠CAB- ∠NAB=50°-40°=10°.
故答案为:10°.
【分析】(1)根据三角形的内角和得∠CAB的度数,根据△AMN和△BMN关于直线MN对称得∠NAB的度数,两角相减即可求得∠CAN的度数.
(2)根据已知△ABC的三边数量关系和其周长,求出△ABC的三边长,根据对称得AN=BN,把△ACN的周长转化为AC+BC来求.
16.【答案】解:根据题意得,a﹣4=0,b﹣9=0,
解得a=4,b=9,
①4是腰长时,三角形的三边分别为4、4、9,
∵4+4<9,
∴不能组成三角形,
②4是底边时,三角形的三边分别为4、9、9,
能组成三角形,周长=9+9+4=22,
所以这个等腰三角形的周长为22.
【解析】【分析】先利用绝对值的非负性求得a,b的值,再由等腰三角形的两边相等,对三角形的边长进行分类讨论,特别需要验证求得的三角形三边是否满足三边关系,将不满足的舍去.
17.【答案】解:如图所示:(3分)
点A的对应点A′的坐标为(3,3);
所得图形为圣诞树.
【解析】【分析】利用轴对称图形的性质得出对应点坐标位置进而画出图象即可.
18.【答案】(1)①120;
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)4
【解析】【解答】(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.
故答案为:120°.
(2)根据轴对称的性质,可知CM=PM,DN=PN,
所以△PMN的周长为:PM+PN+MN=CM+DN+MN=CD=4.
故答案为:4.
【分析】(1)①先求出∠AOC=∠AOP,再求出∠BOD=∠BOP,最后计算求解即可;
②先求出 ∠AOC=∠AOP,再求出∠BOD=∠BOP, 最后计算求解即可;
(2)利用轴对称的性质和三角形的周长公式计算求解即可。
19.【答案】(1)证明:如图1,延长DE交AB于点F,
∵∠ACB+∠BED=180°,∠CED+∠BED=180°,
∴∠ACB=∠CED,
∴AC∥DF,
∴∠A=∠DFB,
∵∠A=∠D,
∴∠DFB=∠D,
∴AB∥CD;
(2)解:如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG=ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3=EDF,
∴ABE+∠β=EDF,
∴∠β=(∠EDF-∠ABE),
∴∠EDF-∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°-∠EDF+∠ABE=180°-(∠EDF-∠ABE)=180°-2∠β,
∵∠DEB比∠DHB大60°,
∴∠α-60°=∠β,
∴∠α=180°-2(∠α-60°),
解得∠α=100°,
∴∠DEB的度数为100°;
(3)解:∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK=EBK,
∠CDN=∠EDN=CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°-∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°-∠EBK=100°,
∴∠EBK-∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN=CDE,
∴∠PBM=∠MBK-∠PBK
=∠EBK-CDE
=(∠EBK-∠CDE)
=80°
=40°.
【解析】【分析】(1) 延长DE交AB于点F, 根据内错角相等,两直线平行性质可判定 AC∥DF ,根据直线平行性质即可求出答案;
(2) 作EM∥CD,HN∥CD, 根据直线平行性质可得:∠1+∠EDF=180°,∠MEB=∠ABE,根据角平分线性质进行角之间的转换得出:∠EDF-∠ABE=2∠β,设∠DEB=∠α,进行角之间的转换即可求出答案;
(3)过点E作ES∥CD,设直线DF和直线BP相交于点G, 根据角平分线性质,直线平行性质可得∠G=∠PBK,由(2)可知∠CDE+180°-∠EBK=100°,根据BP∥DN,∠PBK=∠G=∠CDN=∠CDE,可得:∠PBM=∠MBK-∠PBK即可求出答案。
20.【答案】(1)解:如图,为所作;
(2)解:的面积
(3)解:如图,点为所作,
【解析】【分析】(1)根据作图-轴对称即可求解;
(2)根据割补法即可求解;
(3)根据轴对称(最短路径问题)结合题意画图即可求解。
1 / 1
一、选择题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 ( )
A.30° B.50° C.90° D.100°
3.如图,在中,结合尺规作图的痕迹,已知,的周长为14cm,则的周长是( )
A.17cm B.18cm C.19cm D.20cm
4.如所示四个图案中,不是轴对称图形的是( )
A. B.
C. D.
5.如图,将一张长方形纸片沿 EF折叠后,使得点 A,B 分别落在点A',B'的位置,如果∠2=56°,那么∠1=( )
A.56° B.58° C.62° D.68°
6.小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).
A. B.
C. D.
7.等腰三角形的两边长分别为4和9,则它的周长( )
A.17 B.22 C.17或22 D.21
8.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或120° D.30°或150°
9.如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A.7个 B.8个 C.9个 D.10个
二、填空题
10.小明从镜子里看到对面电子钟的像如图所示,则实际时间是 .
11.如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN= °.
12.如图,在内有一点O到三个顶点的距离相等,连接.若,则的度数为 .
13.如图,在的正方形格纸中,有一个以格点为顶点的,请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
三、解答题
14.如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
15.如图,在中,,点,分别在边,上,连接,且和关于直线对称.
(1)若,则的度数为 .
(2)若,,且的周长为36,求的周长.
16.已知等腰三角形的两边长a、b满足|a﹣4|+(b﹣9)2=0,求这个等腰三角形的周长.
17.如图,请你以y轴为对称轴画出所给图的另一半,若点A坐标为(﹣3,3),写出点A的对应点的坐标,并说明完成后的图形可能代表的含义.
18.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB对称点是D,连接CD交OA于M,交OB于N.
(1)①若∠AOB=60°,则∠COD= °;
②若∠AOB=α,求∠COD的度数.
(2)若CD=4,则△PMN的周长为 .
19.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.
(1)求证:AB∥CD;
(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保持(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
20.方格纸中每个小方格都是边长为的正方形,我们把以格点的连线为边的多边形称为“格点多边形”,如图就是一个“格点三角形”.
(1)画出关于直线的对称图形;
(2)若网格上最小正方形的边长为,求的面积;
(3)若在上存在一点,使得最小,请在图中画出点的位置.
答案解析部分
1.【答案】D
【解析】【解答】A、不是轴对称图形,故A不符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、是轴对称图形,故D符合题意.
故答案为:D.
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐一判断即可.
2.【答案】D
【解析】【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴∠A=∠A′=50°,∠C=∠C′=30°;∴∠B=180°﹣80°=100°.
故答案为:D.
【分析】根据轴对称的性质“成轴对称的两个图形全等”可求解.
3.【答案】B
【解析】【解答】解:由题意可知,DE垂直平分AC;
∴AE=EC,AC=2AD=4,
∴△ABC的周长=AB+BC+AC=AB+BE+AE+AC=14+4=18cm.
故答案为:B.
【分析】根据线段垂直平分线的性质,可得AE=EC,AC=2AD,再根据三角形的周长等于三边之和即可算出答案.
4.【答案】A
【解析】【解答】解:A、选项中的图形找不到一条直线,使直线两旁的部分能够完全重合,则不是轴对称图形,本项符合题意;
B、C、D、选项中可以找到一条直线,使直线两旁的部分能够完全重合,则是轴对称图形,本项不符合题意;
故答案为:A.
【分析】根据轴对称图形的定义:平面内,一个图形沿一条直线折叠 ,直线两旁的部分能够完全重合的图形,据此逐项分析即可.
5.【答案】C
6.【答案】C
【解析】【解答】解:利用轴对称的性质可得,C选项中AC+BC的长最小,
故答案为:C.
【分析】利用“将军饮马”的方法求解即可.
7.【答案】B
【解析】【解答】解:9为腰长时,三角形的周长为9+9+4=22,
9为底边长时,4+4<9,不能组成三角形,
故选:B.
【分析】分类讨论:9为腰长,9为底边长,根据三角形的周长公式,可得答案.
8.【答案】C
【解析】【解答】解:①如图所示:
∵BD⊥AC,
∴∠ADB = 90°,
∵等腰三角形一腰上的高与另一腰的夹角为30°,
∴∠ABD = 30°,
∴∠A = 180°-∠ADB-∠ABD=60°,
即顶角的度数为60°;
②如图所示:
∵BD⊥AC,
∴∠BDC = 90°,
∵等腰三角形一腰上的高与另一腰的夹角为30°,
∴∠ABD = 30°,
∴∠BAD =180°-∠BDC-∠ABD= 60°,
∴∠BAC =180°-∠BAD=120°,
即顶角的度数为120°;
综上所述:它的顶角度数为60°或120°,
故答案为:C.
【分析】根据等腰三角形的性质,结合图形,利用三角形的内角和计算求解即可。
9.【答案】D
【解析】【解答】如图,共有10种符合条件的添法,
故答案为:D.
【分析】根据轴对称的性质画出图形即可.
10.【答案】15:01
【解析】【解答】解:根据平面镜成像原理及轴对称图形的性质可知实际时间为15:01;
故答案为:15:01
【分析】利用平面镜成像原理及轴对称图形的性质可得到实际时间.
11.【答案】40
【解析】【解答】解:∵纸片沿MN折叠,MB与DN交于点K,∠1=70°,
∴∠1=∠BMN=70°.
∵四边形ABCD为矩形,
∴KN∥AM,
∴∠MKN=180°-2∠1=180°-140°=40°.
故答案为:40°.
【分析】根据折叠的性质可得:∠1=∠BMN=70°,由矩形的性质可得KN∥AM,然后根据平行线的性质进行计算.
12.【答案】
【解析】【解答】解:∵O到△ABC三个顶点距离相等,
∴OA=OB=OC,
∴∠CAO=∠ACO=55°,∠ABO=∠BAO=32°,
在△ABC中,∠OCB+∠OBC=180°-55°×2-25°×2=20°,
∴∠BOC=180°-20°=160°.
故答案为:160°.
【分析】由题意可知OA=OB=OC,由等边对等角得,∠CAO=∠ACO=55°,∠ABO=∠BAO=32°,再根据三角形内角和为180°,得出∠OCB+∠OBC=20°,就能求出∠BOC的度数.
13.【答案】5
【解析】【解答】解:与△ABC成轴对称且也以格点为顶点的三角形有5个,
分别为△BCD,△BFH,△ADC,△AEF,△CGH.
故答案为:5.
【分析】根据成轴对称的两个图形沿着对称轴折叠后能够重合画出所有与△ABC成抽对称的三角形,据此解答.
14.【答案】解:∵△ABC和△ADE关于直线l对称,
∴AB=AD,BC=DE,∠B=∠D
又∵AB=15,DE=10,∠D=70°
∴∠B=70°,BC=10,AD=15,
答:∠B=70°,BC=10、AD=15
【解析】【分析】根据对称图形是全等的性质,则对应边相等,对应角也相等, 已知AB和DE的长度,∠D的度数,相应即可求出AD、BC的长度和∠B的度数。
15.【答案】(1)
(2)解:∵的周长为36,
∴,
∵,,
∴,解得,
∴.
∵和关于直线对称,
∴,
∴的周长
【解析】【解答】解:(1)在△ABC中,∠C=90°,∠B=40°,
∴∠CAB=90°-∠B=90°-40°=50°,
∵△AMN和△BMN关于直线MN对称,
∴ ∠NAB=∠B=40°,
∴ ∠CAN=∠CAB- ∠NAB=50°-40°=10°.
故答案为:10°.
【分析】(1)根据三角形的内角和得∠CAB的度数,根据△AMN和△BMN关于直线MN对称得∠NAB的度数,两角相减即可求得∠CAN的度数.
(2)根据已知△ABC的三边数量关系和其周长,求出△ABC的三边长,根据对称得AN=BN,把△ACN的周长转化为AC+BC来求.
16.【答案】解:根据题意得,a﹣4=0,b﹣9=0,
解得a=4,b=9,
①4是腰长时,三角形的三边分别为4、4、9,
∵4+4<9,
∴不能组成三角形,
②4是底边时,三角形的三边分别为4、9、9,
能组成三角形,周长=9+9+4=22,
所以这个等腰三角形的周长为22.
【解析】【分析】先利用绝对值的非负性求得a,b的值,再由等腰三角形的两边相等,对三角形的边长进行分类讨论,特别需要验证求得的三角形三边是否满足三边关系,将不满足的舍去.
17.【答案】解:如图所示:(3分)
点A的对应点A′的坐标为(3,3);
所得图形为圣诞树.
【解析】【分析】利用轴对称图形的性质得出对应点坐标位置进而画出图象即可.
18.【答案】(1)①120;
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2α.
(2)4
【解析】【解答】(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.
故答案为:120°.
(2)根据轴对称的性质,可知CM=PM,DN=PN,
所以△PMN的周长为:PM+PN+MN=CM+DN+MN=CD=4.
故答案为:4.
【分析】(1)①先求出∠AOC=∠AOP,再求出∠BOD=∠BOP,最后计算求解即可;
②先求出 ∠AOC=∠AOP,再求出∠BOD=∠BOP, 最后计算求解即可;
(2)利用轴对称的性质和三角形的周长公式计算求解即可。
19.【答案】(1)证明:如图1,延长DE交AB于点F,
∵∠ACB+∠BED=180°,∠CED+∠BED=180°,
∴∠ACB=∠CED,
∴AC∥DF,
∴∠A=∠DFB,
∵∠A=∠D,
∴∠DFB=∠D,
∴AB∥CD;
(2)解:如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG=ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3=EDF,
∴ABE+∠β=EDF,
∴∠β=(∠EDF-∠ABE),
∴∠EDF-∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°-∠EDF+∠ABE=180°-(∠EDF-∠ABE)=180°-2∠β,
∵∠DEB比∠DHB大60°,
∴∠α-60°=∠β,
∴∠α=180°-2(∠α-60°),
解得∠α=100°,
∴∠DEB的度数为100°;
(3)解:∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK=EBK,
∠CDN=∠EDN=CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°-∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°-∠EBK=100°,
∴∠EBK-∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN=CDE,
∴∠PBM=∠MBK-∠PBK
=∠EBK-CDE
=(∠EBK-∠CDE)
=80°
=40°.
【解析】【分析】(1) 延长DE交AB于点F, 根据内错角相等,两直线平行性质可判定 AC∥DF ,根据直线平行性质即可求出答案;
(2) 作EM∥CD,HN∥CD, 根据直线平行性质可得:∠1+∠EDF=180°,∠MEB=∠ABE,根据角平分线性质进行角之间的转换得出:∠EDF-∠ABE=2∠β,设∠DEB=∠α,进行角之间的转换即可求出答案;
(3)过点E作ES∥CD,设直线DF和直线BP相交于点G, 根据角平分线性质,直线平行性质可得∠G=∠PBK,由(2)可知∠CDE+180°-∠EBK=100°,根据BP∥DN,∠PBK=∠G=∠CDN=∠CDE,可得:∠PBM=∠MBK-∠PBK即可求出答案。
20.【答案】(1)解:如图,为所作;
(2)解:的面积
(3)解:如图,点为所作,
【解析】【分析】(1)根据作图-轴对称即可求解;
(2)根据割补法即可求解;
(3)根据轴对称(最短路径问题)结合题意画图即可求解。
1 / 1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
