人教版九年级数学下册第二十七章 相似 单元复习题(含解析)
文档属性
| 名称 | 人教版九年级数学下册第二十七章 相似 单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 628.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 10:27:30 | ||
图片预览


文档简介
人教版九年级数学下册第二十七章相似单元复习题
一、选择题
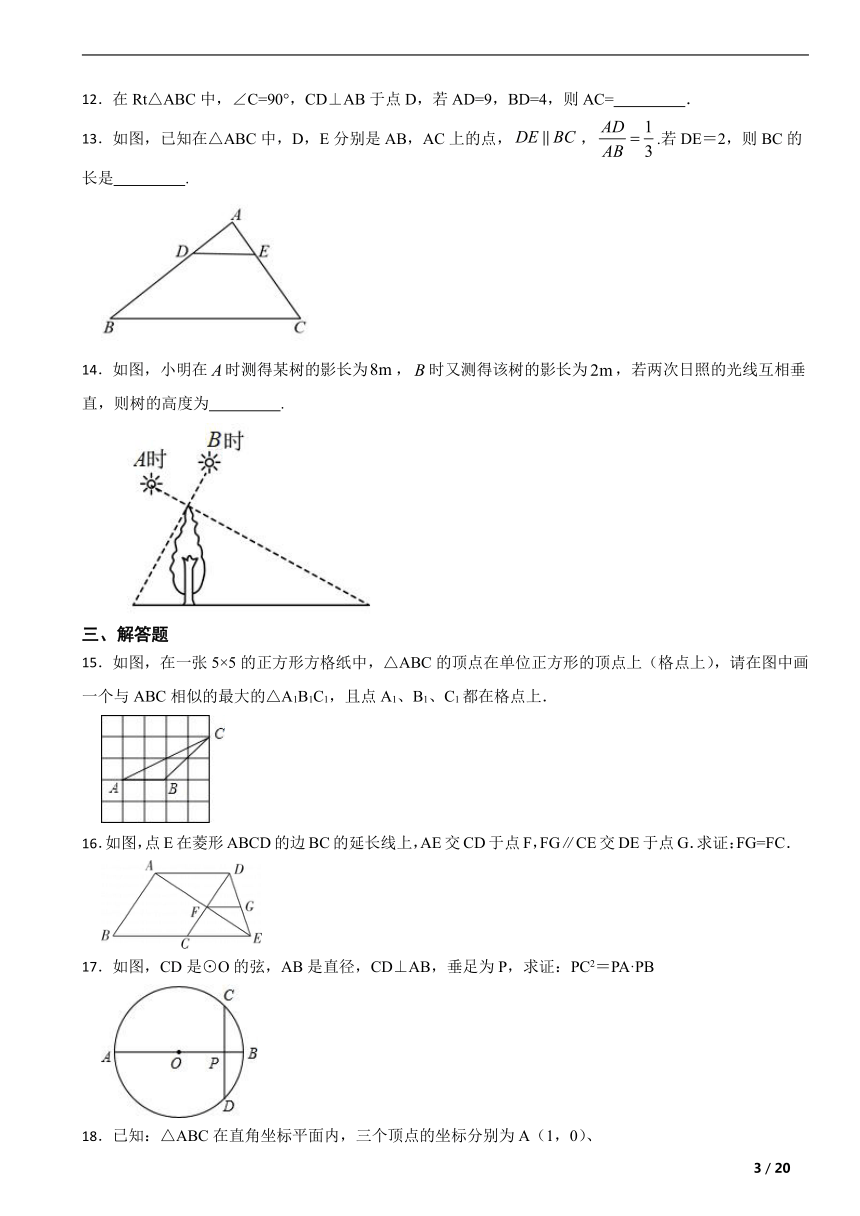
1.下列两个图形一定是相似图形的是( )
A.菱形 B.矩形 C.等腰三角形 D.等边三角形
2.下列各组数中,成比例的是( ).
A.1,-2,-3,-6 B.1,4,2,-8
C.5,6,2,3 D.,,1,
3.如图,AB∥CD,AD,BC相交于点O.若AB=1,CD=2,BO∶CO=( )
A.1∶2 B.1∶4 C.2∶1 D.4∶1
4.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m B.1.6m C.1.86m D.2.16m
5.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
6.如图,在Rt△ABC内画有边长为9,6,x的三个正方形,则x的值为( )
A.3 B.4 C.3 D.5
7.如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( )
A.∠B=∠ACD B.∠ADC=∠ACB C.= D.AC2=AD AB
8.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36 平方米 B.0. 81 平方米
C.2 平方米 D.3.24 平方米
9.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2,则△ABC与△A1B1C1的周长之比是( )
A.1∶4 B.2∶1 C.1∶2 D.1∶3
10.已知一个三角形的其中一个内角是它另外一个内角的两倍,且它的其中一边长是另外一边长的两倍,若它最短的边长为1,则这个三角形的周长不可能是( )
A. B. C. D.
二、填空题
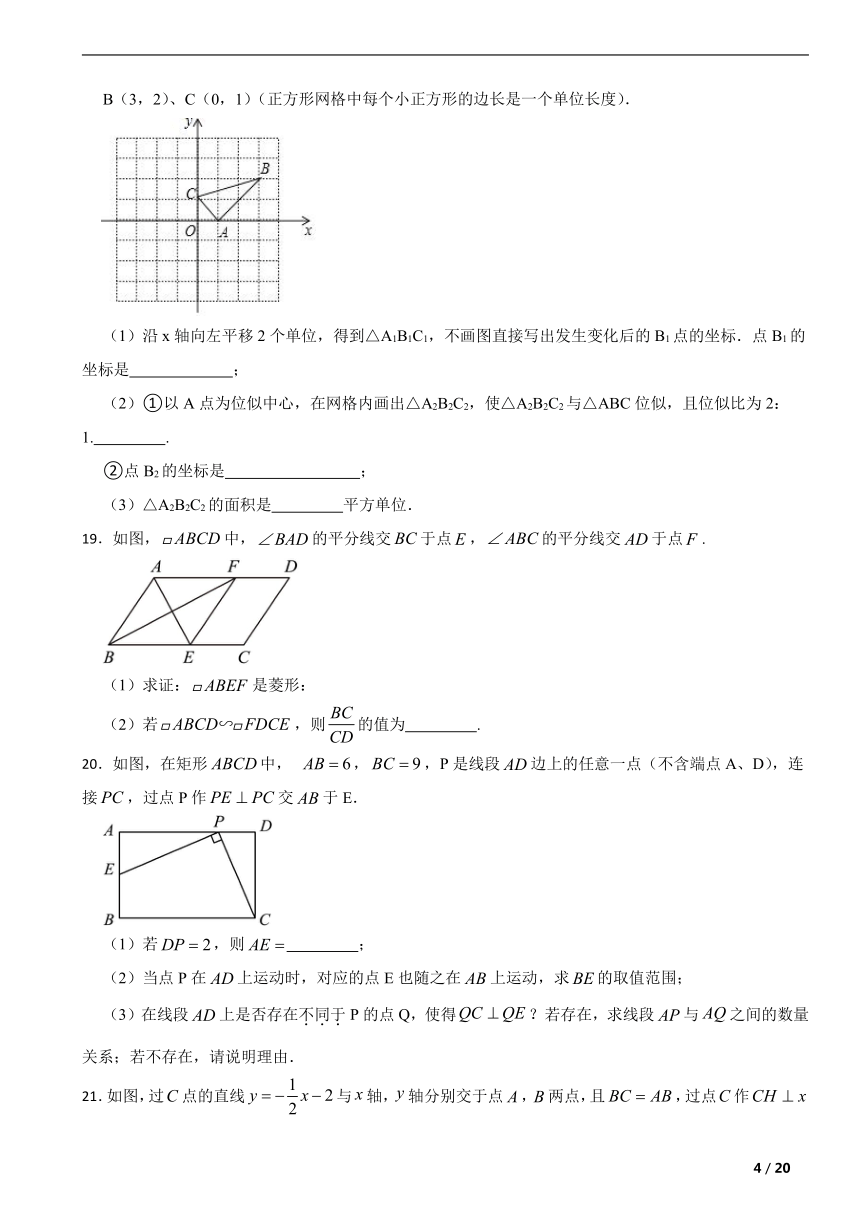
11.如图,已知,如果,,则的长是 .
12.在Rt△ABC中,∠C=90°,CD⊥AB于点D,若AD=9,BD=4,则AC= .
13.如图,已知在△ABC中,D,E分别是AB,AC上的点,,.若DE=2,则BC的长是 .
14.如图,小明在时测得某树的影长为,时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为 .
三、解答题
15.如图,在一张5×5的正方形方格纸中,△ABC的顶点在单位正方形的顶点上(格点上),请在图中画一个与ABC相似的最大的△A1B1C1,且点A1、B1、C1都在格点上.
16.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
17.如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA·PB
18.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
B(3,2)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
(1)沿x轴向左平移2个单位,得到△A1B1C1,不画图直接写出发生变化后的B1点的坐标.点B1的坐标是 ;
(2)①以A点为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1. .
②点B2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
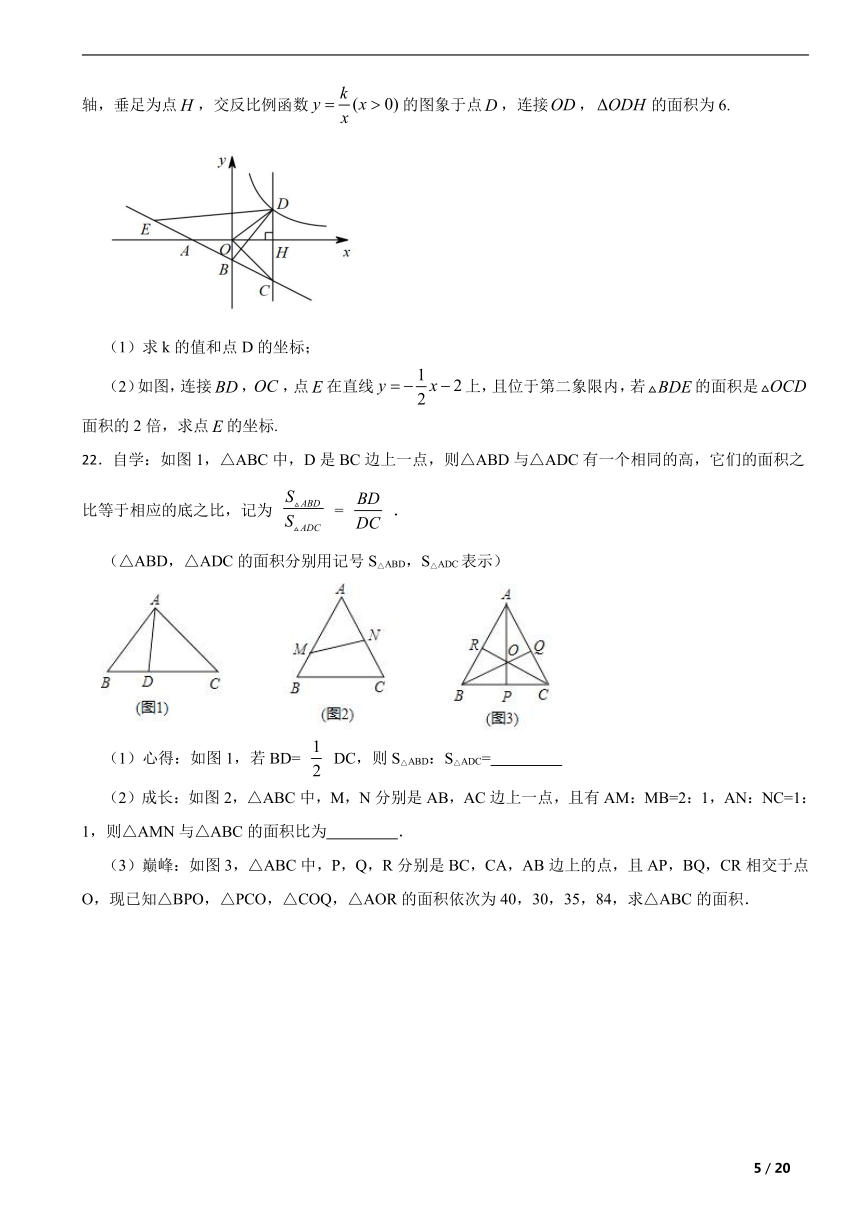
19.如图,中,的平分线交于点,的平分线交于点.
(1)求证:是菱形:
(2)若,则的值为 .
20.如图,在矩形中, ,,P是线段边上的任意一点(不含端点A、D),连接,过点P作交于E.
(1)若,则 ;
(2)当点P在上运动时,对应的点E也随之在上运动,求的取值范围;
(3)在线段上是否存在不同于P的点Q,使得?若存在,求线段与之间的数量关系;若不存在,请说明理由.
21.如图,过点的直线与轴,轴分别交于点,两点,且,过点作轴,垂足为点,交反比例函数的图象于点,连接,的面积为6.
(1)求k的值和点D的坐标;
(2)如图,连接,,点在直线上,且位于第二象限内,若的面积是面积的2倍,求点的坐标.
22.自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 = .
(△ABD,△ADC的面积分别用记号S△ABD,S△ADC表示)
(1)心得:如图1,若BD= DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
答案解析部分
1.【答案】D
【解析】【解答】解:A、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两等腰三角形不一定相似,故此选项不符合题意;
D、两个等边三角形的对应边的比相等,对应角一定相等,故两个等边三角形一定相似,故此选项符合题意.
故答案为:D.
【分析】利用相似多边形的判定:所有的对应边成比例,且所有的对应角分别相等的两个多边形相似,可对A,B作出判断;利用相似三角形的判定定理及等腰三角形的性质,可对C,D作出判断.
2.【答案】D
【解析】【解答】解:A、,不符合题意;
B、,不符合题意;
C、,不符合题意;
D、,符合题意.
故答案为:D.
【分析】如果前两个数据的比值等于后两个数据的比值,那么这四个数据就成比例,据此一一判断得出答案.
3.【答案】A
【解析】【解答】解:∵ AB∥CD,
∴△AOB∽△DOC,
∴.
故答案为:A.
【分析】由平行于三角形一边的直线,截其它两边的延长线,所截的三角形与原三角形相似可得△AOB∽△DOC,进而根据相似三角形对应边成比例即可得出结论.
4.【答案】A
【解析】【解答】∵BE∥AD,
∴△BCE∽△ACD,
∴,即 ,
∵BC=1,DE=1.8,EC=1.2
∴
∴1.2AB=1.8,
∴AB=1.5m.
故答案为:A.
【分析】先证明△BCE∽△ACD,再利用相似三角形的性质可得 ,即 ,再将数据代入计算可得 ,最后求出AB的长即可。
5.【答案】B
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
6.【答案】B
【解析】【解答】解:∵这三个正方形的边都互相平行.
∴它们均相似.
∴ = 解得:x=4.
故选B.
【分析】根据相似多边形的对应边的比相等,就可以判断.
7.【答案】C
【解析】【解答】∵∠A是公共角,
∴再加上∠B=∠ACD,或∠ADC=∠ACB都可判定△ABC∽△ACD,
∵∠A是公共角,再加上AC2=AD AB,即=,也可判定△ABC∽△ACD,
∴选项A、B、D都可判定△ABC∽△ACD.
而选项C中的对两边成比例,但不是相应的夹角相等,所以选项C不能.
故选C.
【分析】根据相似三角形的判定定理对各个选项逐一分析即可.本题考查了相似三角形的判定,此题主要考查学生对相似三角形判定定理的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.
8.【答案】B
【解析】【解答】解:构造如下图形,由题意可得:DE= 米,FG=1米,AG=3米,DE∥BC,AF和AG分别为△ADE和△ABC的高
∴△ADE∽△ABC
∴
即
解得:BC=
∴地面上阴影部分的面积为
故答案为:B.
【分析】先求其直径,二直径可通过构造相似三角形,由相似三角形性质求出。
9.【答案】C
【解析】【解答】解:∵△ABC与△A1B1C1是位似图形,BC∶B1C1=1∶2,
∴△ABC与△A1B1C1的周长之比=BC∶B1C1=1∶2.
故答案为:C.
【分析】根据位似图形的周长比等于相似比进行解答.
10.【答案】D
【解析】【解答】解:如图所示,在中,,过点A作的角平分线交于D,
∴,
∴,
又∵,
∴,
∴,
当时,设,则,
∴,
∴,
∴,
解得,
∴此时三角形的周长为,故B不符合题意;
当时,设,则,
∴,
∴,
∵,
∴此时不能构成三角形;
当时,设,则,
∴
∴,
∴,
解得,
∵,
∴此时不能构成三角形;
当时,设,则,
∴
∴,
∴,
解得,
∵,
∴此时不能构成三角形;
同理可得当,即,可得满足题意的,
∴此时三角形的周长为,故A不符合题意;
同理当,即,可得,
∴此时,不符合题意,即三角形的周长不能为,故D符合题意;
同理当,即,可得,
∴此时三角形的周长为,故C不符合题意;
故答案为:D.
【分析】在△ABC中,∠BAC=2∠B,过点A作∠BAC的角平分线交BC于D,则BD=AD,∠ADC=2∠B=∠BAC,证明△ACD∽△BCA,根据相似三角形的性质可得,①当AC=1、AB=2时,设BC=z,CD=y,则BD=z-y,代入并求解可得z的值,据此可判断B;②当AC=1、BC=2时,设AB=z,CD=y,则BD=AD=2-y,根据相似三角形的性质可得y、z的值,此时不能构成三角形;③当AC=1、BC=2AB时,设AB=z,CD=y,则BD=AD=2z-y,代入求出z的值,此时不能构成三角形;④当AC=1、AB=2BC时,设AB=2z,CD=y,则BD=AD=z-y,同理求出z的值,此时不能构成三角形;⑤当AB=1、BC=2时,设AC=z,CD=y,代入求出AC的值,得到周长,进而判断A;同理判断C、D.
11.【答案】6
【解析】【解答】解:,
,
又AB∶BC=2∶3,,
.
故答案为:6.
【分析】根据平行线分线段成比例的性质可得,然后将已知条件代入计算即可.
12.【答案】
【解析】【解答】如图所示,
∵Rt△ABC中∠C=90°,CD⊥AB,
∴∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴,即CD2=AD BD=9×4=36,解得CD=6,
在Rt△ACD中,
∵AD=9,CD=4,
∴AC=.
故答案为:.
【分析】先根据相似三角形的判定定理得出△ACD∽△CBD,再由相似三角形的对应边成比例求出CD的长,根据勾股定理即可得出AC的长.
13.【答案】6
【解析】【解答】解:根据题意,
∵,
∴△ADE∽△ABC,
∴,
∵DE=2,
∴,
∴;
故答案为:6.
【分析】根据相似三角形的判定"平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似"可得△ADE∽△ABC,由相似三角形的性质可得比例式“”求解.
14.【答案】4m
【解析】【解答】解:根据题意做出示意图,则,,,,
∴,
∴,
∴,
∴,
∴,即,
∴,
∴.
故答案为:4m.
【分析】根据题意做出示意图,则CD⊥EF,CE⊥CF,DE=2m,DF=8m,根据同角的余角相等可得∠E=∠DCF,证明△EDC∽△CDF,然后根据相似三角形的性质进行计算.
15.【答案】解:AB=2,
BC= =2 ,
AC= =2 ,
可作的最大边A1C1= =5 ,
所以,B1C1=2 ,A1B1= ,
△A1B1C1如图所示.
【解析】【分析】利用勾股定理列式求出AB、BC、AC,然后求出可作的最大边A1C1,然后求出A1B1,B1C1,再根据网格结构作出即可.
16.【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
17.【答案】证明:连接AC,BD,
∵∠A=∠D,∠C=∠B,
∴△APC∽△DPB.
∴ ,
∴CP DP=AP BP.
∵AB是直径,CD⊥AB,
∴CP=PD.
∴PC2=PA PB.
【解析】【分析】 连接AC,BD, 利用同弧所对的圆周角相等得∠A=∠D,∠C=∠B,可推出△APC∽△DPB,利用相似三角形的对应边成比例,可证得CP DP=AP BP,利用垂径定理可证得CP=DP,由此可证得结论.
18.【答案】(1)(1,2)
(2);(﹣3,﹣4)
(3)8
【解析】【解答】解:(1.)根据平移规律,将点B(3,2)左平移2个单位,得到点B1的坐标是(1,2),
故答案为:(1,2);
(2.)如图所示,△A2B2C2即为所求,B2(﹣3,﹣4);
故答案为:(﹣3,﹣4);
(3.)△A2B2C2的面积是: ×4×2+ ×4×2=8.
故答案为:8
【分析】(1)直接利用平移的性质,得出各对应点位置进而得出答案;(2)利用位似图形的性质,得出对应点位置进而得出答案;(3)直接利用割补法,求得△A2B2C2面积即可,将该三角形看成上下两部分即可得出答案.
19.【答案】(1)证明:∵的平分线交于点,
∴.
∵四边形是平行四边形,
∴.
∴.
∴.
∴.
同理,.
∴.
∵
∴四边形是平行四边形.
∵,
∴四边形是菱形.
(2)
【解析】【解答】解:(2)由(1)知,四边形是菱形,
又四边形是平行四边形,
,
设,,则有:
,即,
整理得,
解得,
,
,
故答案为:.
【分析】(1)根据角平分线的概念可得∠BAE=∠EAF,根据平行四边形以及平行线的性质可得∠EAF=∠AEB,则∠BAE=∠AEB,推出AB=BE,同理可得AB=AF,则BE=AF,然后根据菱形的判定定理进行证明;
(2)由(1)知:四边形ABEF是菱形,则AB=BE=EF=FA,根据平行四边形的性质可得FD=CE,EF=CD,则AB=BE=EF=FA=CD,使劲儿FD=CE=x,AF=BE=CD=y,则BC=x+y,根据相似图形的对应边成比例可得x,据此求解.
20.【答案】(1)
(2)解:由(1)得:,
,
设,,
,
,
整理得:,
,
当时,,
,
此时的最小值为,
又E在上运动,
,
.
(3)解:如图,假设存在这样的点Q,
由(1)可得:,
同理可得:,
,
,
整理得:,
不同于点,
,
即:不是的中点,
,
∴当P不是的中点时,总存在这样的点Q满足条件,此时.
【解析】【解答】解:(1)∵四边形ABCD为矩形,
∴∠A=∠D=90°,AB=CD=6,BC=AD=9,
∴∠AEP+∠APE=90°.
∵PE⊥PC,
∴∠APE+∠CPD=90°,
∴∠AEP=∠CPD.
∵∠AEP=∠CPD,∠A=∠D=90°,
∴△PAE∽△CDP,
∴,
∴,
∴AE=.
故答案为:.
【分析】(1)根据矩形的性质可得∠A=∠D=90°,AB=CD=6,BC=AD=9,由同角的余角相等可得∠AEP=∠CPD,利用两角对应相等的两个三角形相似可得△PAE∽△CDP,然后由相似三角形的性质进行计算;
(2)由相似三角形的性质可得AE·DC=AP·DP,设AP=x,AE=y,则DP=9-x,代入并整理可得y与x的关系式,由二次函数的性质可得y的最大值以及对应的x的值,然后根据BE=AB-AE可得BE的最小值,根据E在AB上运动可得BE<6,据此可得BE的范围;
(3)假设存在这样的点Q,由(1)可得AE·DC=AP·DP,同理可得AQ·DQ=AE·DC,则AQ·DQ=AP·DP,结合DQ=9-AQ、DP=9-AP可得AP+AQ-9=0,据此解答.
21.【答案】(1)解:设点坐标为,由题意得,
,
点在的图象上,
,
直线的图象与轴交于点,
点的坐标为,
轴,
轴,
,
,
点的横坐标为4.
点在反比例函数的图象上
点坐标为;
(2)解:由(1)知轴,
,
,
,
过点作,垂足为点,交轴于点,
,,
,
,
点的横坐标为
点在直线上,
点的坐标为.
【解析】【分析】(1)设D(m,n),由三角形的面积公式可得mn=6,求出mn的值,结合点D在反比例函数图象上可得k的值,令直线解析式中的y=0,求出x的值,可得点A的坐标,根据平行线分线段成比例的性质可得OH=AO=4,即点D的横坐标为4,将x=4代入反比例函数解析式中求出y的值,据此可得点D的坐标;
(2)由(1)可知CD∥y轴,则S△BCD=S△OCD,由题意可得S△BDE=2S△OCD,则S△EDC=3S△BCD,过点E作EF⊥CD,垂足为点F,交y轴于点M,根据△EDC、△BCD的面积公式可得EF=3OH=12,则EM=8,即点E的横坐标为-8,将x=-8代入直线解析式中求出y的值,据此可得点E的坐标.
22.【答案】(1)1:2
(2)1:3
(3)解:设△BRO和△AOQ的面积分别为x、y,
∵△BPO,△PCO的面积分别为40,30,
∴ = ,
∴ = ,即 = ,
=2,
∴OB=2OQ,
∴ =2,即 =2,
则 ,
解得, ,
∴△ABC的面积为:40+30+35+84+60+72=321
【解析】【解答】解:心得:∵BD= DC,
∴ = ,
∴S△ABD:S△ADC=1:2,
故答案为:1:2;
成长:如图②.连接BN,
∵AN:NC=1:1,
∴S△ANB=S△CNB= S△ABC,
∵AM:MB=2:1,
∴SAMN= S△ANB,
∴△AMN与△ABC的面积比为1:3,
故答案为:1:3;
巅峰:
【分析】心得:根据两个三角形有一个相同的高,它们的面积之比等于相应的底之比进行计算即可;成长:连接BN,根据题意求出S△ANB=S△CNB= S△ABC,SAMN= S△ANB,计算即可;巅峰:设△BRO和△AOQ的面积分别为x、y,根据题意列出二元一次方程组,解方程组即可.
1 / 1
一、选择题
1.下列两个图形一定是相似图形的是( )
A.菱形 B.矩形 C.等腰三角形 D.等边三角形
2.下列各组数中,成比例的是( ).
A.1,-2,-3,-6 B.1,4,2,-8
C.5,6,2,3 D.,,1,
3.如图,AB∥CD,AD,BC相交于点O.若AB=1,CD=2,BO∶CO=( )
A.1∶2 B.1∶4 C.2∶1 D.4∶1
4.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m B.1.6m C.1.86m D.2.16m
5.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
6.如图,在Rt△ABC内画有边长为9,6,x的三个正方形,则x的值为( )
A.3 B.4 C.3 D.5
7.如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( )
A.∠B=∠ACD B.∠ADC=∠ACB C.= D.AC2=AD AB
8.如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为( )
A.0.36 平方米 B.0. 81 平方米
C.2 平方米 D.3.24 平方米
9.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2,则△ABC与△A1B1C1的周长之比是( )
A.1∶4 B.2∶1 C.1∶2 D.1∶3
10.已知一个三角形的其中一个内角是它另外一个内角的两倍,且它的其中一边长是另外一边长的两倍,若它最短的边长为1,则这个三角形的周长不可能是( )
A. B. C. D.
二、填空题
11.如图,已知,如果,,则的长是 .
12.在Rt△ABC中,∠C=90°,CD⊥AB于点D,若AD=9,BD=4,则AC= .
13.如图,已知在△ABC中,D,E分别是AB,AC上的点,,.若DE=2,则BC的长是 .
14.如图,小明在时测得某树的影长为,时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为 .
三、解答题
15.如图,在一张5×5的正方形方格纸中,△ABC的顶点在单位正方形的顶点上(格点上),请在图中画一个与ABC相似的最大的△A1B1C1,且点A1、B1、C1都在格点上.
16.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
17.如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA·PB
18.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
B(3,2)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
(1)沿x轴向左平移2个单位,得到△A1B1C1,不画图直接写出发生变化后的B1点的坐标.点B1的坐标是 ;
(2)①以A点为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1. .
②点B2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
19.如图,中,的平分线交于点,的平分线交于点.
(1)求证:是菱形:
(2)若,则的值为 .
20.如图,在矩形中, ,,P是线段边上的任意一点(不含端点A、D),连接,过点P作交于E.
(1)若,则 ;
(2)当点P在上运动时,对应的点E也随之在上运动,求的取值范围;
(3)在线段上是否存在不同于P的点Q,使得?若存在,求线段与之间的数量关系;若不存在,请说明理由.
21.如图,过点的直线与轴,轴分别交于点,两点,且,过点作轴,垂足为点,交反比例函数的图象于点,连接,的面积为6.
(1)求k的值和点D的坐标;
(2)如图,连接,,点在直线上,且位于第二象限内,若的面积是面积的2倍,求点的坐标.
22.自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为 = .
(△ABD,△ADC的面积分别用记号S△ABD,S△ADC表示)
(1)心得:如图1,若BD= DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
答案解析部分
1.【答案】D
【解析】【解答】解:A、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两等腰三角形不一定相似,故此选项不符合题意;
D、两个等边三角形的对应边的比相等,对应角一定相等,故两个等边三角形一定相似,故此选项符合题意.
故答案为:D.
【分析】利用相似多边形的判定:所有的对应边成比例,且所有的对应角分别相等的两个多边形相似,可对A,B作出判断;利用相似三角形的判定定理及等腰三角形的性质,可对C,D作出判断.
2.【答案】D
【解析】【解答】解:A、,不符合题意;
B、,不符合题意;
C、,不符合题意;
D、,符合题意.
故答案为:D.
【分析】如果前两个数据的比值等于后两个数据的比值,那么这四个数据就成比例,据此一一判断得出答案.
3.【答案】A
【解析】【解答】解:∵ AB∥CD,
∴△AOB∽△DOC,
∴.
故答案为:A.
【分析】由平行于三角形一边的直线,截其它两边的延长线,所截的三角形与原三角形相似可得△AOB∽△DOC,进而根据相似三角形对应边成比例即可得出结论.
4.【答案】A
【解析】【解答】∵BE∥AD,
∴△BCE∽△ACD,
∴,即 ,
∵BC=1,DE=1.8,EC=1.2
∴
∴1.2AB=1.8,
∴AB=1.5m.
故答案为:A.
【分析】先证明△BCE∽△ACD,再利用相似三角形的性质可得 ,即 ,再将数据代入计算可得 ,最后求出AB的长即可。
5.【答案】B
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
6.【答案】B
【解析】【解答】解:∵这三个正方形的边都互相平行.
∴它们均相似.
∴ = 解得:x=4.
故选B.
【分析】根据相似多边形的对应边的比相等,就可以判断.
7.【答案】C
【解析】【解答】∵∠A是公共角,
∴再加上∠B=∠ACD,或∠ADC=∠ACB都可判定△ABC∽△ACD,
∵∠A是公共角,再加上AC2=AD AB,即=,也可判定△ABC∽△ACD,
∴选项A、B、D都可判定△ABC∽△ACD.
而选项C中的对两边成比例,但不是相应的夹角相等,所以选项C不能.
故选C.
【分析】根据相似三角形的判定定理对各个选项逐一分析即可.本题考查了相似三角形的判定,此题主要考查学生对相似三角形判定定理的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.
8.【答案】B
【解析】【解答】解:构造如下图形,由题意可得:DE= 米,FG=1米,AG=3米,DE∥BC,AF和AG分别为△ADE和△ABC的高
∴△ADE∽△ABC
∴
即
解得:BC=
∴地面上阴影部分的面积为
故答案为:B.
【分析】先求其直径,二直径可通过构造相似三角形,由相似三角形性质求出。
9.【答案】C
【解析】【解答】解:∵△ABC与△A1B1C1是位似图形,BC∶B1C1=1∶2,
∴△ABC与△A1B1C1的周长之比=BC∶B1C1=1∶2.
故答案为:C.
【分析】根据位似图形的周长比等于相似比进行解答.
10.【答案】D
【解析】【解答】解:如图所示,在中,,过点A作的角平分线交于D,
∴,
∴,
又∵,
∴,
∴,
当时,设,则,
∴,
∴,
∴,
解得,
∴此时三角形的周长为,故B不符合题意;
当时,设,则,
∴,
∴,
∵,
∴此时不能构成三角形;
当时,设,则,
∴
∴,
∴,
解得,
∵,
∴此时不能构成三角形;
当时,设,则,
∴
∴,
∴,
解得,
∵,
∴此时不能构成三角形;
同理可得当,即,可得满足题意的,
∴此时三角形的周长为,故A不符合题意;
同理当,即,可得,
∴此时,不符合题意,即三角形的周长不能为,故D符合题意;
同理当,即,可得,
∴此时三角形的周长为,故C不符合题意;
故答案为:D.
【分析】在△ABC中,∠BAC=2∠B,过点A作∠BAC的角平分线交BC于D,则BD=AD,∠ADC=2∠B=∠BAC,证明△ACD∽△BCA,根据相似三角形的性质可得,①当AC=1、AB=2时,设BC=z,CD=y,则BD=z-y,代入并求解可得z的值,据此可判断B;②当AC=1、BC=2时,设AB=z,CD=y,则BD=AD=2-y,根据相似三角形的性质可得y、z的值,此时不能构成三角形;③当AC=1、BC=2AB时,设AB=z,CD=y,则BD=AD=2z-y,代入求出z的值,此时不能构成三角形;④当AC=1、AB=2BC时,设AB=2z,CD=y,则BD=AD=z-y,同理求出z的值,此时不能构成三角形;⑤当AB=1、BC=2时,设AC=z,CD=y,代入求出AC的值,得到周长,进而判断A;同理判断C、D.
11.【答案】6
【解析】【解答】解:,
,
又AB∶BC=2∶3,,
.
故答案为:6.
【分析】根据平行线分线段成比例的性质可得,然后将已知条件代入计算即可.
12.【答案】
【解析】【解答】如图所示,
∵Rt△ABC中∠C=90°,CD⊥AB,
∴∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴,即CD2=AD BD=9×4=36,解得CD=6,
在Rt△ACD中,
∵AD=9,CD=4,
∴AC=.
故答案为:.
【分析】先根据相似三角形的判定定理得出△ACD∽△CBD,再由相似三角形的对应边成比例求出CD的长,根据勾股定理即可得出AC的长.
13.【答案】6
【解析】【解答】解:根据题意,
∵,
∴△ADE∽△ABC,
∴,
∵DE=2,
∴,
∴;
故答案为:6.
【分析】根据相似三角形的判定"平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似"可得△ADE∽△ABC,由相似三角形的性质可得比例式“”求解.
14.【答案】4m
【解析】【解答】解:根据题意做出示意图,则,,,,
∴,
∴,
∴,
∴,
∴,即,
∴,
∴.
故答案为:4m.
【分析】根据题意做出示意图,则CD⊥EF,CE⊥CF,DE=2m,DF=8m,根据同角的余角相等可得∠E=∠DCF,证明△EDC∽△CDF,然后根据相似三角形的性质进行计算.
15.【答案】解:AB=2,
BC= =2 ,
AC= =2 ,
可作的最大边A1C1= =5 ,
所以,B1C1=2 ,A1B1= ,
△A1B1C1如图所示.
【解析】【分析】利用勾股定理列式求出AB、BC、AC,然后求出可作的最大边A1C1,然后求出A1B1,B1C1,再根据网格结构作出即可.
16.【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
17.【答案】证明:连接AC,BD,
∵∠A=∠D,∠C=∠B,
∴△APC∽△DPB.
∴ ,
∴CP DP=AP BP.
∵AB是直径,CD⊥AB,
∴CP=PD.
∴PC2=PA PB.
【解析】【分析】 连接AC,BD, 利用同弧所对的圆周角相等得∠A=∠D,∠C=∠B,可推出△APC∽△DPB,利用相似三角形的对应边成比例,可证得CP DP=AP BP,利用垂径定理可证得CP=DP,由此可证得结论.
18.【答案】(1)(1,2)
(2);(﹣3,﹣4)
(3)8
【解析】【解答】解:(1.)根据平移规律,将点B(3,2)左平移2个单位,得到点B1的坐标是(1,2),
故答案为:(1,2);
(2.)如图所示,△A2B2C2即为所求,B2(﹣3,﹣4);
故答案为:(﹣3,﹣4);
(3.)△A2B2C2的面积是: ×4×2+ ×4×2=8.
故答案为:8
【分析】(1)直接利用平移的性质,得出各对应点位置进而得出答案;(2)利用位似图形的性质,得出对应点位置进而得出答案;(3)直接利用割补法,求得△A2B2C2面积即可,将该三角形看成上下两部分即可得出答案.
19.【答案】(1)证明:∵的平分线交于点,
∴.
∵四边形是平行四边形,
∴.
∴.
∴.
∴.
同理,.
∴.
∵
∴四边形是平行四边形.
∵,
∴四边形是菱形.
(2)
【解析】【解答】解:(2)由(1)知,四边形是菱形,
又四边形是平行四边形,
,
设,,则有:
,即,
整理得,
解得,
,
,
故答案为:.
【分析】(1)根据角平分线的概念可得∠BAE=∠EAF,根据平行四边形以及平行线的性质可得∠EAF=∠AEB,则∠BAE=∠AEB,推出AB=BE,同理可得AB=AF,则BE=AF,然后根据菱形的判定定理进行证明;
(2)由(1)知:四边形ABEF是菱形,则AB=BE=EF=FA,根据平行四边形的性质可得FD=CE,EF=CD,则AB=BE=EF=FA=CD,使劲儿FD=CE=x,AF=BE=CD=y,则BC=x+y,根据相似图形的对应边成比例可得x,据此求解.
20.【答案】(1)
(2)解:由(1)得:,
,
设,,
,
,
整理得:,
,
当时,,
,
此时的最小值为,
又E在上运动,
,
.
(3)解:如图,假设存在这样的点Q,
由(1)可得:,
同理可得:,
,
,
整理得:,
不同于点,
,
即:不是的中点,
,
∴当P不是的中点时,总存在这样的点Q满足条件,此时.
【解析】【解答】解:(1)∵四边形ABCD为矩形,
∴∠A=∠D=90°,AB=CD=6,BC=AD=9,
∴∠AEP+∠APE=90°.
∵PE⊥PC,
∴∠APE+∠CPD=90°,
∴∠AEP=∠CPD.
∵∠AEP=∠CPD,∠A=∠D=90°,
∴△PAE∽△CDP,
∴,
∴,
∴AE=.
故答案为:.
【分析】(1)根据矩形的性质可得∠A=∠D=90°,AB=CD=6,BC=AD=9,由同角的余角相等可得∠AEP=∠CPD,利用两角对应相等的两个三角形相似可得△PAE∽△CDP,然后由相似三角形的性质进行计算;
(2)由相似三角形的性质可得AE·DC=AP·DP,设AP=x,AE=y,则DP=9-x,代入并整理可得y与x的关系式,由二次函数的性质可得y的最大值以及对应的x的值,然后根据BE=AB-AE可得BE的最小值,根据E在AB上运动可得BE<6,据此可得BE的范围;
(3)假设存在这样的点Q,由(1)可得AE·DC=AP·DP,同理可得AQ·DQ=AE·DC,则AQ·DQ=AP·DP,结合DQ=9-AQ、DP=9-AP可得AP+AQ-9=0,据此解答.
21.【答案】(1)解:设点坐标为,由题意得,
,
点在的图象上,
,
直线的图象与轴交于点,
点的坐标为,
轴,
轴,
,
,
点的横坐标为4.
点在反比例函数的图象上
点坐标为;
(2)解:由(1)知轴,
,
,
,
过点作,垂足为点,交轴于点,
,,
,
,
点的横坐标为
点在直线上,
点的坐标为.
【解析】【分析】(1)设D(m,n),由三角形的面积公式可得mn=6,求出mn的值,结合点D在反比例函数图象上可得k的值,令直线解析式中的y=0,求出x的值,可得点A的坐标,根据平行线分线段成比例的性质可得OH=AO=4,即点D的横坐标为4,将x=4代入反比例函数解析式中求出y的值,据此可得点D的坐标;
(2)由(1)可知CD∥y轴,则S△BCD=S△OCD,由题意可得S△BDE=2S△OCD,则S△EDC=3S△BCD,过点E作EF⊥CD,垂足为点F,交y轴于点M,根据△EDC、△BCD的面积公式可得EF=3OH=12,则EM=8,即点E的横坐标为-8,将x=-8代入直线解析式中求出y的值,据此可得点E的坐标.
22.【答案】(1)1:2
(2)1:3
(3)解:设△BRO和△AOQ的面积分别为x、y,
∵△BPO,△PCO的面积分别为40,30,
∴ = ,
∴ = ,即 = ,
=2,
∴OB=2OQ,
∴ =2,即 =2,
则 ,
解得, ,
∴△ABC的面积为:40+30+35+84+60+72=321
【解析】【解答】解:心得:∵BD= DC,
∴ = ,
∴S△ABD:S△ADC=1:2,
故答案为:1:2;
成长:如图②.连接BN,
∵AN:NC=1:1,
∴S△ANB=S△CNB= S△ABC,
∵AM:MB=2:1,
∴SAMN= S△ANB,
∴△AMN与△ABC的面积比为1:3,
故答案为:1:3;
巅峰:
【分析】心得:根据两个三角形有一个相同的高,它们的面积之比等于相应的底之比进行计算即可;成长:连接BN,根据题意求出S△ANB=S△CNB= S△ABC,SAMN= S△ANB,计算即可;巅峰:设△BRO和△AOQ的面积分别为x、y,根据题意列出二元一次方程组,解方程组即可.
1 / 1
