6.2.1向量的加法运算 课件(共37张PPT)-人教A版(2019)高中数学必修第二册课件
文档属性
| 名称 | 6.2.1向量的加法运算 课件(共37张PPT)-人教A版(2019)高中数学必修第二册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 796.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:25:47 | ||
图片预览

文档简介
(共37张PPT)
6.2.1向量的加法运算
平行四边形法则
C
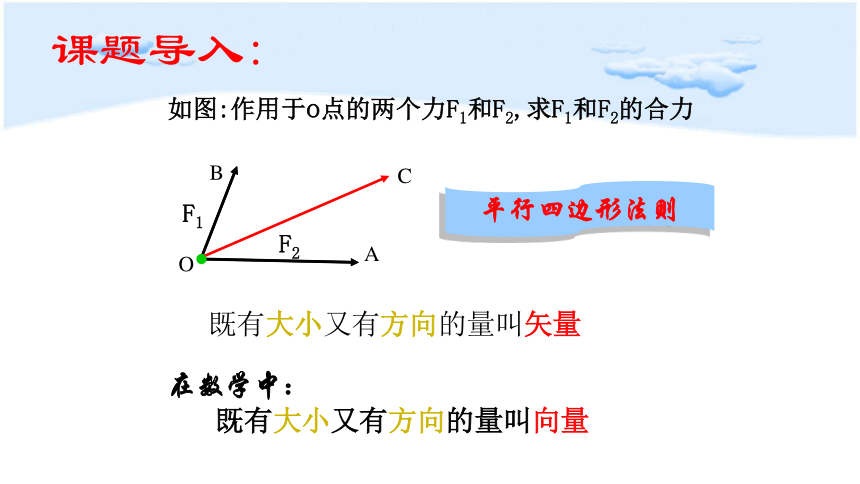
课题导入:
如图:作用于o点的两个力F1和F2,求F1和F2的合力
既有大小又有方向的量叫矢量
F1
B
O
A
F2
在数学中:
既有大小又有方向的量叫向量
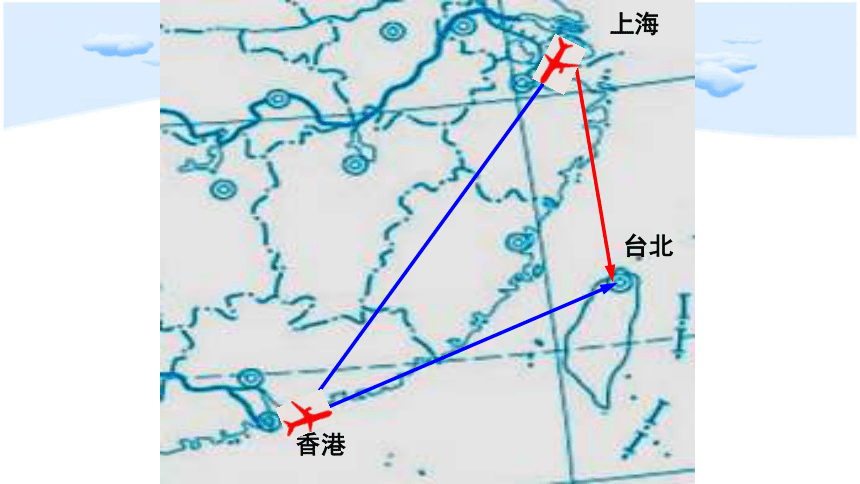
上海
香港
台北
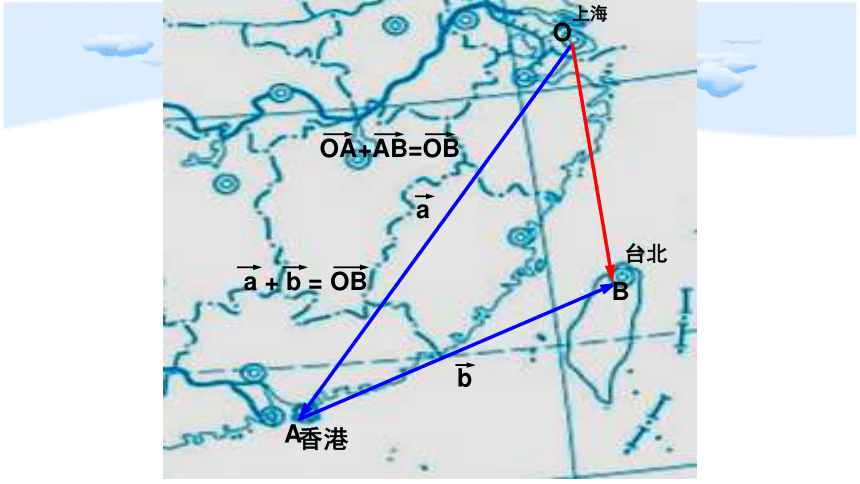
上海
香港
台北
O
A
B
OA+AB=OB
a
b
a + b = OB
a
b
a
b
B
C
A
A
A
A
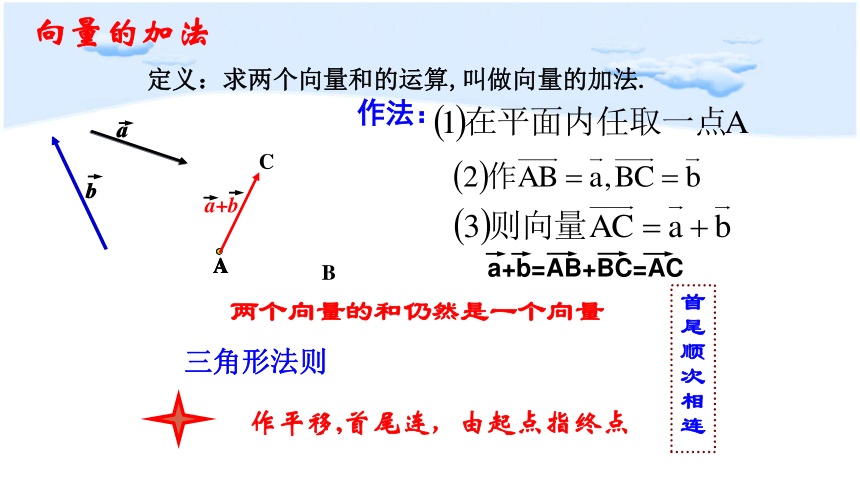
定义:求两个向量和的运算,叫做向量的加法.
向量的加法
a+b=AB+BC=AC
三角形法则
两个向量的和仍然是一个向量
作平移,首尾连,由起点指终点
作法:
a+b
首尾顺次相连
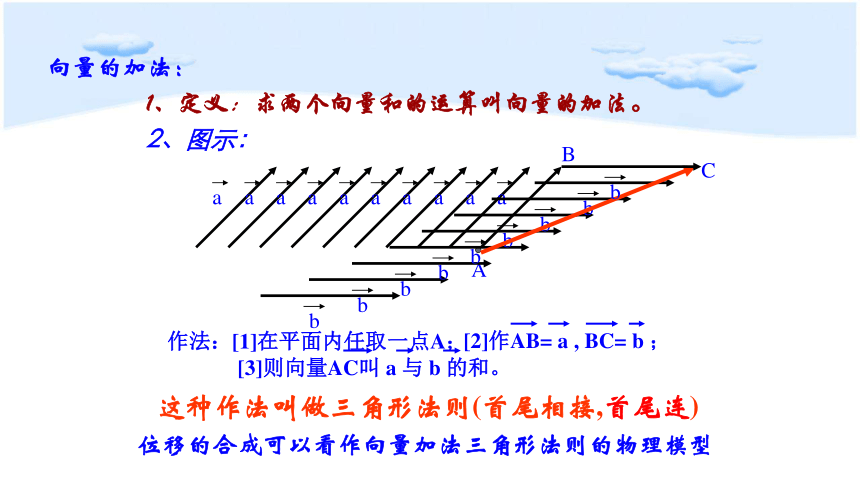
向量的加法:
1、定义:求两个向量和的运算叫向量的加法。
2、图示:
b
a
A
a
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
作法:[1]在平面内任取一点A;
这种作法叫做三角形法则(首尾相接,首尾连)
C
b
B
[2]作AB= a , BC= b ;
[3]则向量AC叫 a 与 b 的和。
位移的合成可以看作向量加法三角形法则的物理模型
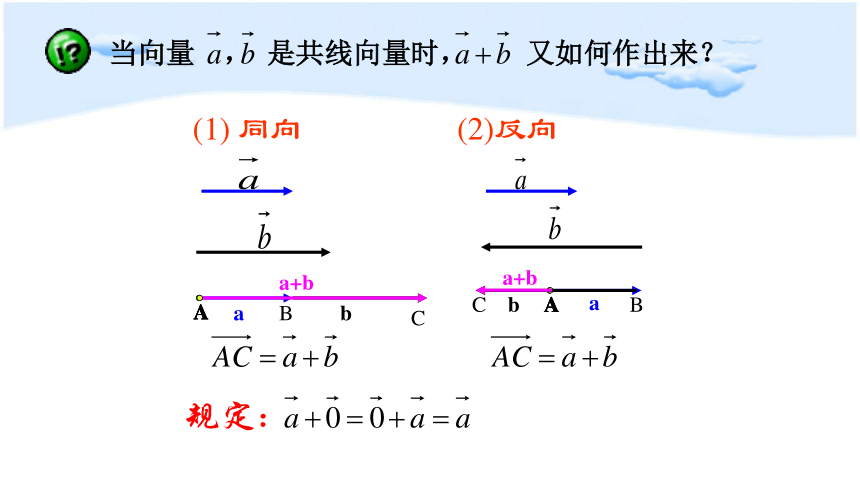
(1) 同向
(2)反向
a
B
C
B
C
规定:
当向量 , 是共线向量时, 又如何作出来?
A
A
A
A
a
b
a+b
A
A
A
A
b
a+b
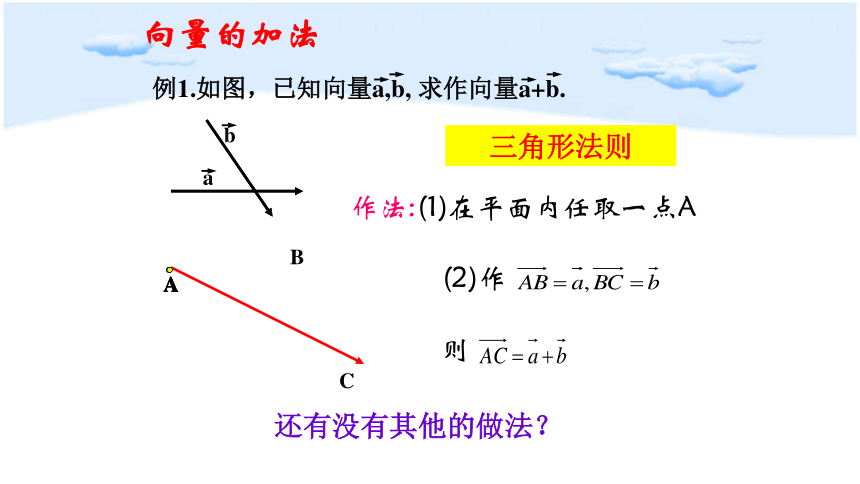
例1.如图,已知向量a,b, 求作向量a+b.
B
a
b
C
向量的加法
(2)作
作法:(1)在平面内任取一点A
则
还有没有其他的做法?
A
A
A
A
三角形法则
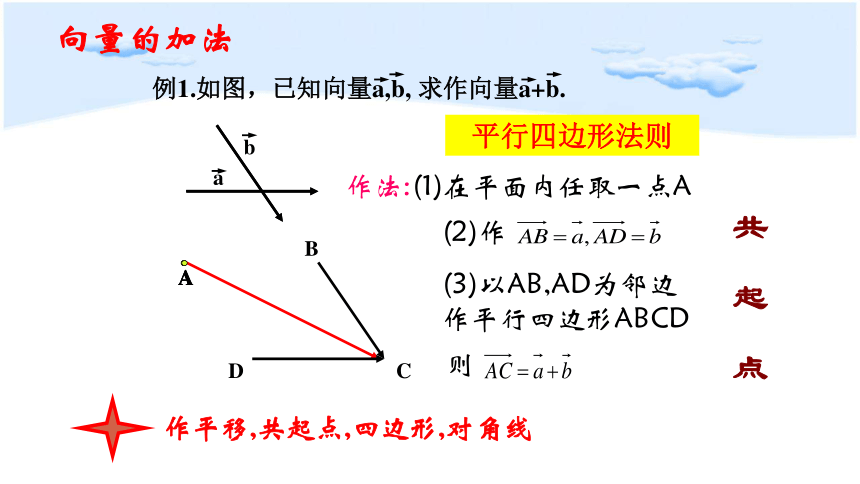
例1.如图,已知向量a,b, 求作向量a+b.
B
a
b
C
D
向量的加法
A
A
A
A
作法:(1)在平面内任取一点A
(2)作
则
(3)以AB,AD为邻边作平行四边形ABCD
平行四边形法则
作平移,共起点,四边形,对角线
共 起 点
a
b
O
A
B
a
a
a
b
b
b
b
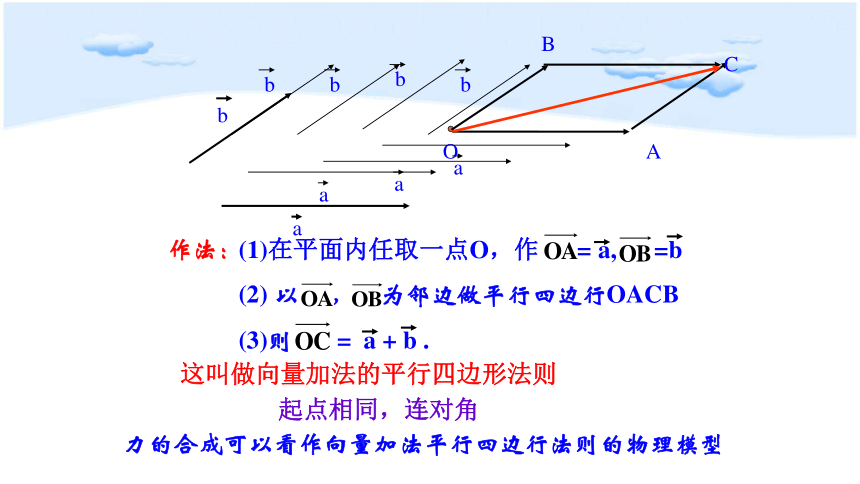
这叫做向量加法的平行四边形法则
(1)在平面内任取一点O,作 = a, =b
C
起点相同,连对角
(2) 以 , 为邻边做平行四边行OACB
(3)则 = a + b .
作法:
力的合成可以看作向量加法平行四边行法则的物理模型
A1
A2
A3
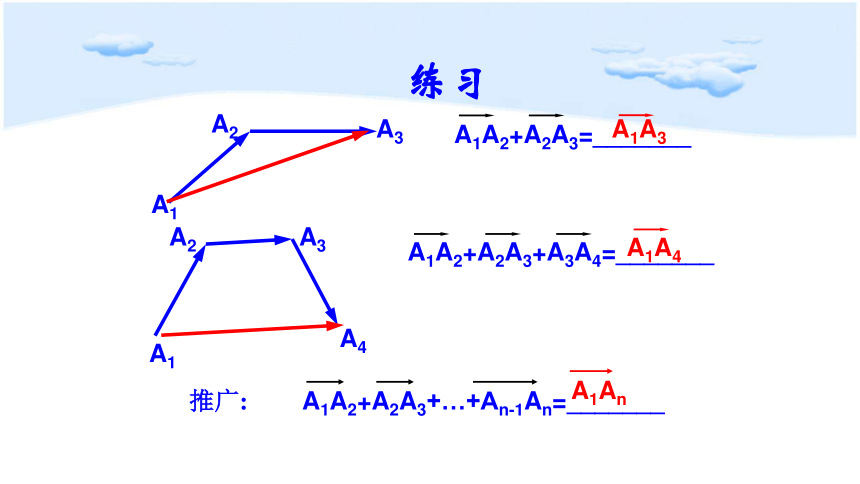
A1A2+A2A3=_______
练习
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
推广:
A1A2+A2A3+…+An-1An=_______
A1An
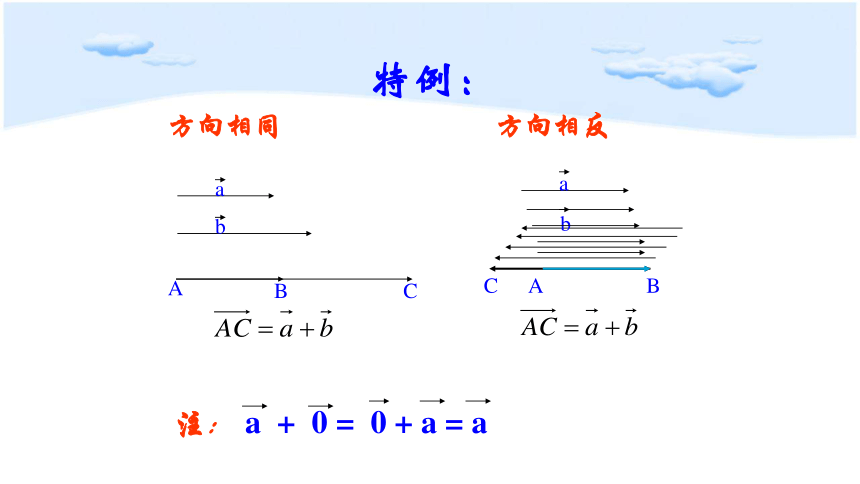
特例:
a
b
A
B
C
方向相同
a
b
C
A
B
方向相反
注: a + 0 = 0 + a = a
a
b
a
b
(2)
b
a
(4)
a
b
(1)
(3)
A
A
A
A
C
B
A
A
A
A
A
A
A
A
B
B
C
C
a + b
a
b
a
b
a+b
b
a
a + b
a + b
1.如图,已知a、b,用向量加法的三角形法则作出 a+b.
课堂练习
(1)
a
b
A
a
b
(2)
A
B
B
C
C
D
D
课堂练习
a
b
a + b
a
b
a + b
2.如图,已知a、b,用向量加法的平行四边形法则作出 a+b.
1.由例1知,当a,b不共线时,
有__________________.
a
C
b
B
A
a
b
A
B
C
a
b
C
A
B
2.当a,b共线时,且
(1)当a与b同向时,
有____________________.
(2)当a与b反向时,
有___________________.
探究 与 的关系:
因此,我们有
两个向量的和仍然是向量,那么它的大小和方向怎样呢?
东
北
A
B
30
C
D
北
B
30
C
例1轮船从A港沿东偏北 方向行驶了40
海里到达B处,再由B处沿正北方向行驶40海里到达C处.求此时轮船与A港的相对位置.
向量加法的运算律
数的加法满足交换律和结合律,即对任意 ,有
a+b=b+a,
(a+b)+c=a+(b+c).
① a + b = b + a
② ( a + b ) + c = a + ( b + c )
任意向量 的加法是否也满足交换律和结合律?
探究 向量加法的运算律
数的加法满足交换律和结合律,即对任意 ,有
a+b=b+a,
(a+b)+c=a+(b+c).
① a + b = b + a
② ( a + b ) + c = a + ( b + c )
任意向量 的加法是否也满足交换律和结合律?
成立
成立
以上两个性质可以推广到任意多个向量
向量加法的运算律
结合律: 成立吗?
交换律:
对于任意的向量 , , :
根据相等向量的定义得:
如图:以A为起点,作向量 ,以AB,AD为邻边作平行四边形ABCD.
a+b
a
b
a
b
A
B
C
D
对角线 是两向量和.
a+b
a+b
a+b
向量加法的运算律
交换律:
a+(b+c)=OA+_____=______
O
(a+b)+c=_____+____=______
OB
OC
AC
A
B
C
OC
BC
a
b
c
a
c
b
所以 成立
( a + b ) + c = a + ( b + c )
结合律:
2.根据图示填空:
(1) a + b =
(2) c + d =
(3) a + b + d =
(4) c + d + e =
D
C
A
B
O
a
b
c
d
a
c
b
E
D
C
A
B
d
e
f
g
DA
CB
g
f
c
f
课堂练习(二)
1.根据图示填空
A1
A2
A3
A1A2+A2A3=_______
探究
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
探究
A1An+1
A1
A2
A3
An+1
An
A4
A1A2+A2A3+…+ AnAn+1=_______
若平面内有n个首尾相接的向量,构成一个折线,那么这n个向量的和是多少呢
多边形法则
探究
0
A1
A2
A3
An
An-1
A4
A1A2+A2A3+…+ An-1An+AnA1 +=_______
若平面内有n个首尾相接的向量,构成一个封闭图形,那么这n个向量的和是多少呢
例2 两个力F1和F2同时作用在一个物体上,其中F1 =40N,方向向东,F2=30N,方向向北,求它们的合力.
东
北
O
B
θ
C
A
B
F1
F2
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1=3.46km/h,河水流动的速度v2=2.0km/h,试求小船过河实际航行速度的大小和方向.
O
B
A
C
1.化简
1.向量
2.在矩形ABCD中, 等于( )
A.
B.
C.
D.
3.已知正方形ABCD的边长为1,
则 的模为( )
A. 0 B. 3 C. D.
D
C
课堂检测
4.下列说法:
①在△ABC中,必有 ;
②若 ,则A、B、C为一个三角形的
三个顶点;
③若 、 均为非零向量,则 与 一定
相等.
其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
B
长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。
A
D
B
C
答:船实际航行速度为4km/h,方向与水的流速间的夹角为60 。
A
D
B
C
如图,作OA=a,OB=b,
以OA、OB为邻边作平行四边行,
则BC=_____,AC=_____.
O
A
C
B
a
b
a
b
a+b
a+b=____+_____=______
b+a=____+_____=______
所以 成立
a + b = b + a
a
b
OA
AC
OC
OB
BC
OC
验证向量加法交换律
1.向量加法的定义
2.向量加法的两种法则:
小结
(1)三角形法则:
(2)平行四边形法则:
3.向量加法的运算律:
交换律:
结合律:
作平移,共起点,四边形,对角线
作平移,首尾连,由起点指终点
6.2.1向量的加法运算
平行四边形法则
C
课题导入:
如图:作用于o点的两个力F1和F2,求F1和F2的合力
既有大小又有方向的量叫矢量
F1
B
O
A
F2
在数学中:
既有大小又有方向的量叫向量
上海
香港
台北
上海
香港
台北
O
A
B
OA+AB=OB
a
b
a + b = OB
a
b
a
b
B
C
A
A
A
A
定义:求两个向量和的运算,叫做向量的加法.
向量的加法
a+b=AB+BC=AC
三角形法则
两个向量的和仍然是一个向量
作平移,首尾连,由起点指终点
作法:
a+b
首尾顺次相连
向量的加法:
1、定义:求两个向量和的运算叫向量的加法。
2、图示:
b
a
A
a
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
作法:[1]在平面内任取一点A;
这种作法叫做三角形法则(首尾相接,首尾连)
C
b
B
[2]作AB= a , BC= b ;
[3]则向量AC叫 a 与 b 的和。
位移的合成可以看作向量加法三角形法则的物理模型
(1) 同向
(2)反向
a
B
C
B
C
规定:
当向量 , 是共线向量时, 又如何作出来?
A
A
A
A
a
b
a+b
A
A
A
A
b
a+b
例1.如图,已知向量a,b, 求作向量a+b.
B
a
b
C
向量的加法
(2)作
作法:(1)在平面内任取一点A
则
还有没有其他的做法?
A
A
A
A
三角形法则
例1.如图,已知向量a,b, 求作向量a+b.
B
a
b
C
D
向量的加法
A
A
A
A
作法:(1)在平面内任取一点A
(2)作
则
(3)以AB,AD为邻边作平行四边形ABCD
平行四边形法则
作平移,共起点,四边形,对角线
共 起 点
a
b
O
A
B
a
a
a
b
b
b
b
这叫做向量加法的平行四边形法则
(1)在平面内任取一点O,作 = a, =b
C
起点相同,连对角
(2) 以 , 为邻边做平行四边行OACB
(3)则 = a + b .
作法:
力的合成可以看作向量加法平行四边行法则的物理模型
A1
A2
A3
A1A2+A2A3=_______
练习
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
推广:
A1A2+A2A3+…+An-1An=_______
A1An
特例:
a
b
A
B
C
方向相同
a
b
C
A
B
方向相反
注: a + 0 = 0 + a = a
a
b
a
b
(2)
b
a
(4)
a
b
(1)
(3)
A
A
A
A
C
B
A
A
A
A
A
A
A
A
B
B
C
C
a + b
a
b
a
b
a+b
b
a
a + b
a + b
1.如图,已知a、b,用向量加法的三角形法则作出 a+b.
课堂练习
(1)
a
b
A
a
b
(2)
A
B
B
C
C
D
D
课堂练习
a
b
a + b
a
b
a + b
2.如图,已知a、b,用向量加法的平行四边形法则作出 a+b.
1.由例1知,当a,b不共线时,
有__________________.
a
C
b
B
A
a
b
A
B
C
a
b
C
A
B
2.当a,b共线时,且
(1)当a与b同向时,
有____________________.
(2)当a与b反向时,
有___________________.
探究 与 的关系:
因此,我们有
两个向量的和仍然是向量,那么它的大小和方向怎样呢?
东
北
A
B
30
C
D
北
B
30
C
例1轮船从A港沿东偏北 方向行驶了40
海里到达B处,再由B处沿正北方向行驶40海里到达C处.求此时轮船与A港的相对位置.
向量加法的运算律
数的加法满足交换律和结合律,即对任意 ,有
a+b=b+a,
(a+b)+c=a+(b+c).
① a + b = b + a
② ( a + b ) + c = a + ( b + c )
任意向量 的加法是否也满足交换律和结合律?
探究 向量加法的运算律
数的加法满足交换律和结合律,即对任意 ,有
a+b=b+a,
(a+b)+c=a+(b+c).
① a + b = b + a
② ( a + b ) + c = a + ( b + c )
任意向量 的加法是否也满足交换律和结合律?
成立
成立
以上两个性质可以推广到任意多个向量
向量加法的运算律
结合律: 成立吗?
交换律:
对于任意的向量 , , :
根据相等向量的定义得:
如图:以A为起点,作向量 ,以AB,AD为邻边作平行四边形ABCD.
a+b
a
b
a
b
A
B
C
D
对角线 是两向量和.
a+b
a+b
a+b
向量加法的运算律
交换律:
a+(b+c)=OA+_____=______
O
(a+b)+c=_____+____=______
OB
OC
AC
A
B
C
OC
BC
a
b
c
a
c
b
所以 成立
( a + b ) + c = a + ( b + c )
结合律:
2.根据图示填空:
(1) a + b =
(2) c + d =
(3) a + b + d =
(4) c + d + e =
D
C
A
B
O
a
b
c
d
a
c
b
E
D
C
A
B
d
e
f
g
DA
CB
g
f
c
f
课堂练习(二)
1.根据图示填空
A1
A2
A3
A1A2+A2A3=_______
探究
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
探究
A1An+1
A1
A2
A3
An+1
An
A4
A1A2+A2A3+…+ AnAn+1=_______
若平面内有n个首尾相接的向量,构成一个折线,那么这n个向量的和是多少呢
多边形法则
探究
0
A1
A2
A3
An
An-1
A4
A1A2+A2A3+…+ An-1An+AnA1 +=_______
若平面内有n个首尾相接的向量,构成一个封闭图形,那么这n个向量的和是多少呢
例2 两个力F1和F2同时作用在一个物体上,其中F1 =40N,方向向东,F2=30N,方向向北,求它们的合力.
东
北
O
B
θ
C
A
B
F1
F2
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1=3.46km/h,河水流动的速度v2=2.0km/h,试求小船过河实际航行速度的大小和方向.
O
B
A
C
1.化简
1.向量
2.在矩形ABCD中, 等于( )
A.
B.
C.
D.
3.已知正方形ABCD的边长为1,
则 的模为( )
A. 0 B. 3 C. D.
D
C
课堂检测
4.下列说法:
①在△ABC中,必有 ;
②若 ,则A、B、C为一个三角形的
三个顶点;
③若 、 均为非零向量,则 与 一定
相等.
其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
B
长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。
A
D
B
C
答:船实际航行速度为4km/h,方向与水的流速间的夹角为60 。
A
D
B
C
如图,作OA=a,OB=b,
以OA、OB为邻边作平行四边行,
则BC=_____,AC=_____.
O
A
C
B
a
b
a
b
a+b
a+b=____+_____=______
b+a=____+_____=______
所以 成立
a + b = b + a
a
b
OA
AC
OC
OB
BC
OC
验证向量加法交换律
1.向量加法的定义
2.向量加法的两种法则:
小结
(1)三角形法则:
(2)平行四边形法则:
3.向量加法的运算律:
交换律:
结合律:
作平移,共起点,四边形,对角线
作平移,首尾连,由起点指终点
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
