6.3.1平面向量基本定理 课件(共18张PPT)-人教A版(2019)高中数学必修第二册课件
文档属性
| 名称 | 6.3.1平面向量基本定理 课件(共18张PPT)-人教A版(2019)高中数学必修第二册课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 17:36:31 | ||
图片预览





文档简介
(共18张PPT)
人教A版高中数学必修第二册
6.3.1 平面向量基本定理
向量 与非零向量 共线,则有且只有一个实数 ,使得:
温故知新
向量共线定理:
长度:
1. 当 时,
与 方向相同;
方向:
2. 当 时,
与 方向相反;
3. 当 时,
引入新课
我们知道,已知两个力,可以求出它们的合力;反过来,一个力可以分解为两个力。如图所示,我们可以根据解决实际问题的需要,通过作平行四边形,将力F分解为多组大小、方向不同的分力。
由力的分解得到启发,我们能否通过作平行四边形,将向量 分解为两个向量,使向量 是这两个向量的和呢?
课堂探究
O
C
A
B
M
N
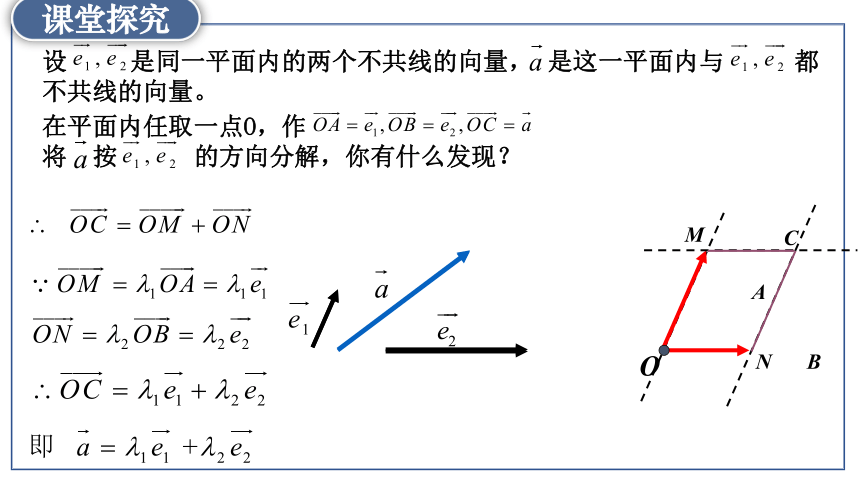
设 是同一平面内的两个不共线的向量, 是这一平面内与 都不共线的向量。
在平面内任取一点O,作
将 按 的方向分解,你有什么发现?
课堂探究
思考 :若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
e2
a
a=λ1e1+0e2
a=0e1+λ2e2
e2
e1
课堂探究
e1
e2
a
N
M
e1
e2
o
a
C
a
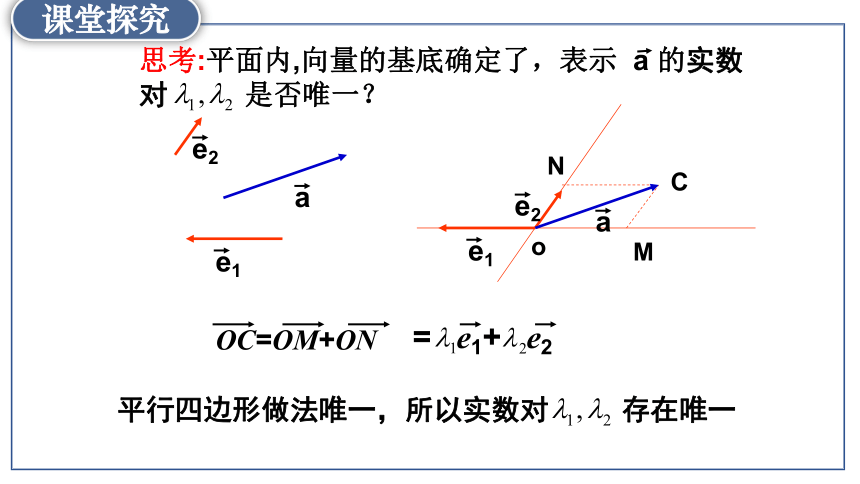
思考:平面内,向量的基底确定了,表示 的实数
对 是否唯一?
OC=OM+ON
= e1+ e2
平行四边形做法唯一,所以实数对 存在唯一
引入新知
平面向量基本定理
如果 、 是同 一平面内的两个不共线的向量,那么对于这一平面内的任何向量 ,有且只有一对实数 ,使
若 不共线,我们把 叫做表示这一平面内
所有向量的一个基底。
一组平面向量的基底有多少对?
(有无数对)
思考:
E
F
F
A
N
B
a
M
O
C
N
M
M
O
C
N
a
E
课堂探究
1、基底不唯一,关键是不共线.
3、基底给定时,分解形式唯一.
2、由定理可将任一向量 在给出基底
的条件下进行分解.
注意
课堂练习
(2)
A
B
C
D
例1
已知:OA,OB不共线,AP=tAB,(t∈R),
用OA,OB表示OP。
B
O
A
P
解:∵AP = t AB
∴OP = OA + AP
= OA + t AB
= OA + t(OB – OA)
= OA + tOB – tOA
=(1 - t)OA + tOB
课堂典例
课堂典例
解 ∵四边形ABCD是平行四边形,E、F分别是BC、DC边上的中点,
课堂练习
课堂典例
课堂典例
巩固练习
巩固练面向量基本定理
如果 、 是同 一平面内的两个不共线的向量,那么对于这一平面内的任何向量 ,有且只有一对实数 ,使
若 不共线,我们把 叫做表示这一平面内
所有向量的一个基底。
课堂小结
人教A版高中数学必修第二册
6.3.1 平面向量基本定理
向量 与非零向量 共线,则有且只有一个实数 ,使得:
温故知新
向量共线定理:
长度:
1. 当 时,
与 方向相同;
方向:
2. 当 时,
与 方向相反;
3. 当 时,
引入新课
我们知道,已知两个力,可以求出它们的合力;反过来,一个力可以分解为两个力。如图所示,我们可以根据解决实际问题的需要,通过作平行四边形,将力F分解为多组大小、方向不同的分力。
由力的分解得到启发,我们能否通过作平行四边形,将向量 分解为两个向量,使向量 是这两个向量的和呢?
课堂探究
O
C
A
B
M
N
设 是同一平面内的两个不共线的向量, 是这一平面内与 都不共线的向量。
在平面内任取一点O,作
将 按 的方向分解,你有什么发现?
课堂探究
思考 :若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
e2
a
a=λ1e1+0e2
a=0e1+λ2e2
e2
e1
课堂探究
e1
e2
a
N
M
e1
e2
o
a
C
a
思考:平面内,向量的基底确定了,表示 的实数
对 是否唯一?
OC=OM+ON
= e1+ e2
平行四边形做法唯一,所以实数对 存在唯一
引入新知
平面向量基本定理
如果 、 是同 一平面内的两个不共线的向量,那么对于这一平面内的任何向量 ,有且只有一对实数 ,使
若 不共线,我们把 叫做表示这一平面内
所有向量的一个基底。
一组平面向量的基底有多少对?
(有无数对)
思考:
E
F
F
A
N
B
a
M
O
C
N
M
M
O
C
N
a
E
课堂探究
1、基底不唯一,关键是不共线.
3、基底给定时,分解形式唯一.
2、由定理可将任一向量 在给出基底
的条件下进行分解.
注意
课堂练习
(2)
A
B
C
D
例1
已知:OA,OB不共线,AP=tAB,(t∈R),
用OA,OB表示OP。
B
O
A
P
解:∵AP = t AB
∴OP = OA + AP
= OA + t AB
= OA + t(OB – OA)
= OA + tOB – tOA
=(1 - t)OA + tOB
课堂典例
课堂典例
解 ∵四边形ABCD是平行四边形,E、F分别是BC、DC边上的中点,
课堂练习
课堂典例
课堂典例
巩固练习
巩固练面向量基本定理
如果 、 是同 一平面内的两个不共线的向量,那么对于这一平面内的任何向量 ,有且只有一对实数 ,使
若 不共线,我们把 叫做表示这一平面内
所有向量的一个基底。
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
