6.3.1二项式定理 课件(共44张PPT)-数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.3.1二项式定理 课件(共44张PPT)-数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 920.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 20:53:50 | ||
图片预览





文档简介
(共44张PPT)
6.3.1 二项式定理
新课讲解
(a+b)2
(a+b)3
那么将(a+b)4 ,(a+b)5 . . .展开后,它们的各项是什么呢?
=C20 a2 + C21 ab+ C22 b2
= C30a3 +C31a2b+C32ab2 +C33 b3
=a3 + 3a2b+3ab2 + b3
= a2 +2ab+b2
展开下面式子
新课讲解
(a+b)2= (a+b) (a+b)
展开后其项的形式为:a2 , ab , b2
这三项的系数为各项在展开式中出现的次数.
考虑b:
每个都不取b的情况有C20 种,则a2前的系数为C20
恰有1个取b的情况有C21种,则ab前的系数为C21
恰有2个取b的情况有C22 种,则b2前的系数为C22
(a+b)2 = a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
对(a+b)2展开式的分析
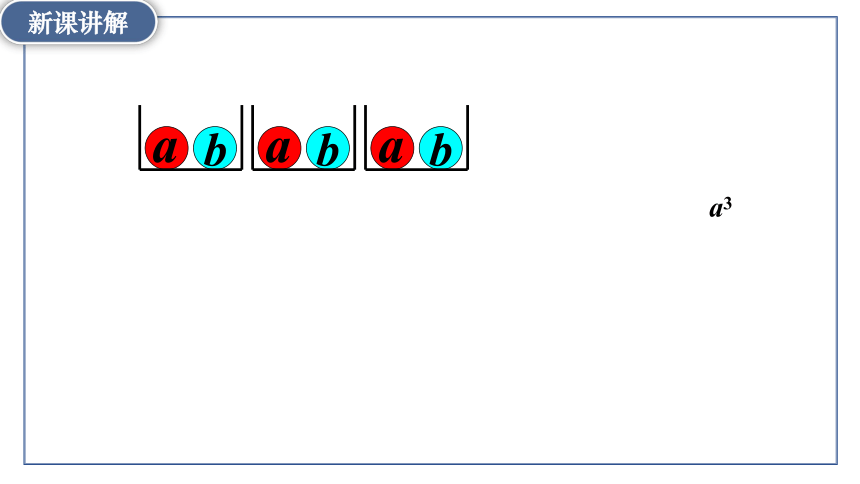
a3
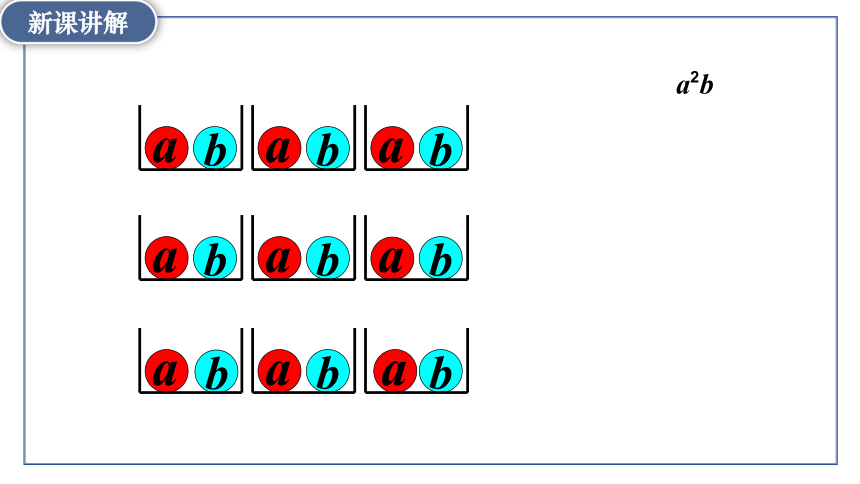
以 为例体会组合思想
新课讲解
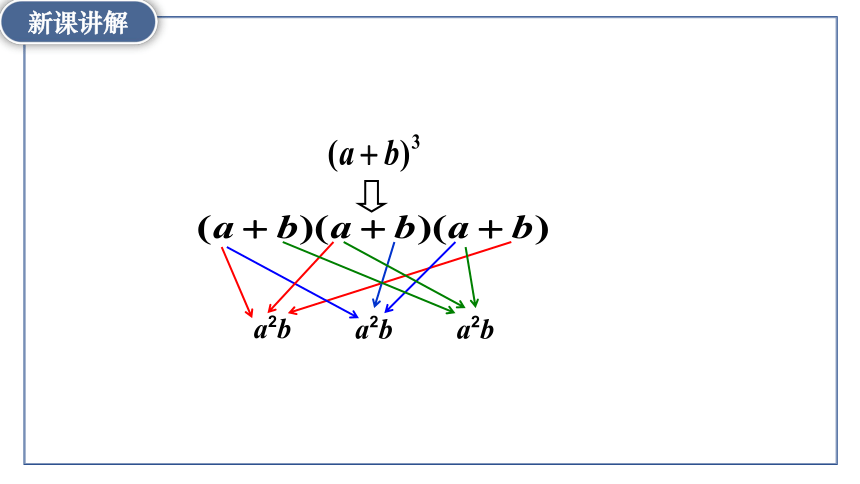
a2b
a2b
a2b
新课讲解
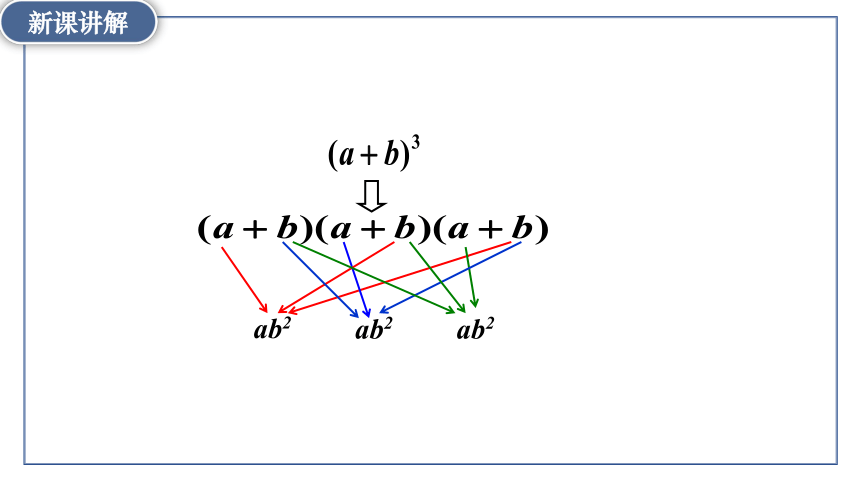
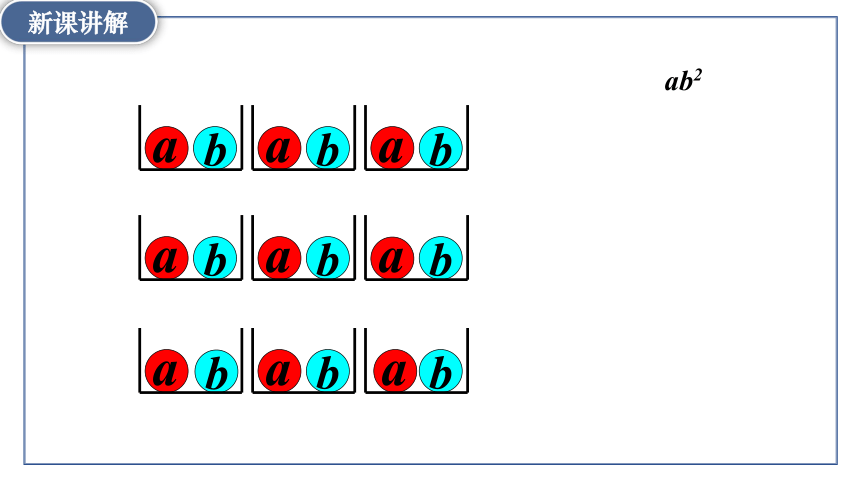
ab2
ab2
ab2
新课讲解
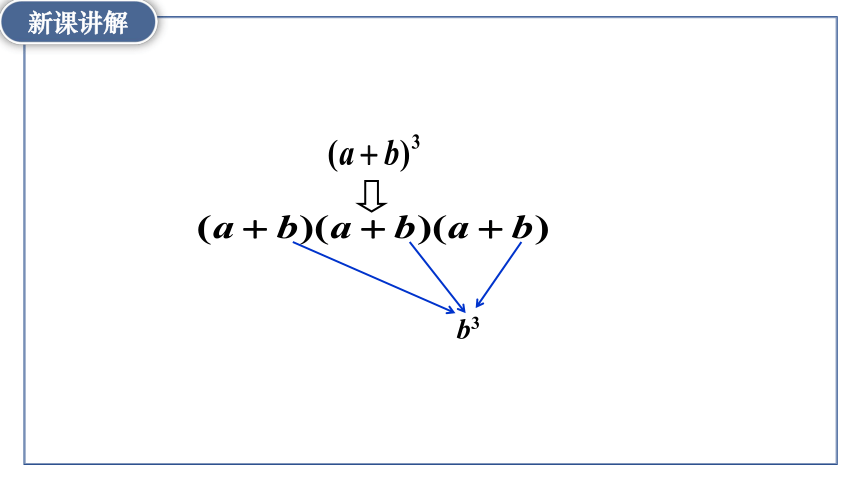
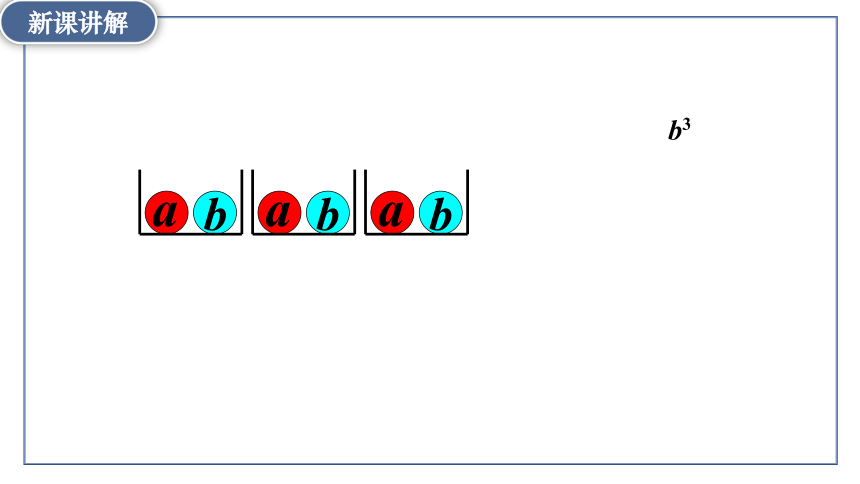
b3
新课讲解
a3
a2b
ab2
b3
新课讲解
a3
新课讲解
a2b
新课讲解
ab2
新课讲解
b3
新课讲解
新课讲解
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
(1)(a+b)4展开后各项形式分别是什么?
(2)各项前的系数代表着什么?
a4 a3b a2b2 ab3 b4
各项前的系数 代表着这些项在展开式中出现的次数
问题
新课讲解
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则
(a+b)4 =C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(3)你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=
新课讲解
二项式定理
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
新课讲解
右边的多项式叫做(a+b)n的二项展开式
Cnk an-kbk:二项展开式的通项,记作Tk+1
Cnk : 二项式系数
①二项展开式共有n+1项
②各项中a的指数从n起依次减小1,到0为止,
各项中b的指数从0起依次增加1,到n为止.
如(1+x)n = Cn0 + Cn1 x+ Cn2 x2+ … +Cnk xk +…+ xn
注
二项式定理
典型例题
例1
解:
典型例题
例2
求(1+2x)7的展开式的第4项
第4项的二项式系数
第4项的系数
解
(1+2x)7的展开式的第4项是
T3+1=C73 17-3 (2x)3 =35×23×x3 =280x3
第4项的二项式系数是C73 =35
第4项的系数是280
归纳小结
注:(1)注意对二项式定理的灵活应用
(2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
(3)求二项式系数或项的系数的一种方法是将二项式展开
典型例题
例3
(1)第4项;
(2)第4项的二项式系数;
(3)第4项的系数;
(4)含x4项的系数;
(5)常数项;
(6)有理项.
求二项展开式的特定项的常见题型:
①求第k项,Tk=Cnk-1an-k+1bk-1;
②求含xk的项(或 xpyq 的项);
③求常数项;
④求有理项.
方法:根据通项Tk+1=Cnkan-kbk,建立方程求k,再将k的值代回通项求解,注意k的取值范围(k=0,1,2,…,n).
方法归纳
巩固训练
1. 求(x+a)12的展开式中的倒数第4项
解:
(1)(x+a)12的展开式有13项,倒数第4项是它的第10项
归纳小结
1)注意二项式定理中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
例4
(1)(2017·卷1) 展开式中x2的系数为( ) A. 15 B. 20 C. 30 D. 35
多项式乘二项式
典型例题
(2)(2014·卷1) 的展开式中 系数为____.
(3)求 的展开式中的 系数。
求多项式乘二项展开式中的特定项的一般方法:
(1)将多项式中的每一项与二项展开式的通项相乘,得到符合要求的项;
(2)将所有符合要求的项加起来.
方法归纳
例5
(x+y+z)9 中含 x4y2z3 的项的系数是_____
三项式问题
典型例题
典型例题
三项式转化为二项式
解:三项式不能用二项式定理,必须转化为二项式
再利用二项式定理逐项分析常数项得
例6
例7
(2015·卷1) 的展开式中, 系数为____.
典型例题
巩固训练
________
解:
原式化为
其通项公式为
240
括号里含有三项的情况可以把某两项合并为一项,合并时要注意选择的科学性.也可因式分解化为乘积二项式.
求三项展开式中的特定项的一般方法:
(1)利用组合原理,分组计算再求和;
(2)将三项式变成二项式,二次展开.
方法归纳
6.3.1 二项式定理
第二课时
温故知新
1.(a+b)n的二项展开式 是_________.
2.通项公式是 _______________.
Tr+1 =
5.在 展开式中的常数项是____
典型例题
例1、计算:
(1)
(2)
新课讲解
分析:本题的左边是一个数列但不能直接求和.
因为 由此分析求解
两式相加
新课讲解
典型例题
求多项式的展开式中特定的项(系数)
例3
的展开式中, 的系数等于___________
解:仔细观察所给已知条件可直接求得 的系
数是
解法2
运用等比数列求和公式得
在 的展开式中,含有 项的系数为
所以 的系数为-20
求复杂的代数式的展开式中某项(某项的系数),可以逐项分析求解,常常对所给代数式进行化简,可以减小计算量
典型例题
求展开式中系数最大(小)的项
解:
设 项是系数最大的项,则
二项式系数最大的项为第11项,即
所以它们的比是
解决系数最大问题,通常设第 项是系数最大的项,则有
由此确定r的取值
方法总结
变式训练
练习 在 的展开式中,系数绝对值最大的项
解:设系数绝对值最大的项是第r+1项,则
所以当 时,系数绝对值最大的项为
新课讲解
例5:已知a,b∈N,m,n ∈Z ,且2m + n = 0,如果二项式( ax m + bx n )12 的展开式中系数最大的项恰好是常数项,求 a : b 的取值范围。
解:
令m (12 – r )+ nr = 0,将 n =﹣2m 代入,解得 r = 4
故T5 为常数项,且系数最大。
变式训练
2. 已知 的第5项的二项式系数与第3 项的二项式系数比为14:3,求展开式中不含x 的项。
3. 已知 的展开式中,第5项的系数与第3 项的系数比为56:3,求展开式中的常数项。
1. 已知 展开式中第2项大于它的相邻两项,求x的范围。
典型例题
例6 若 展开式中前三项系数成等差数列,
求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。
巩固练习
1. 已知 的展开式中x3的系数
为 ,则常数a的值是_______
2. 在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 207
3. (x+y+z)9中含x4y2z3的项的系数是__________
4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值.
本节课你有哪些收获?请做一下总结!
小结
6.3.1 二项式定理
新课讲解
(a+b)2
(a+b)3
那么将(a+b)4 ,(a+b)5 . . .展开后,它们的各项是什么呢?
=C20 a2 + C21 ab+ C22 b2
= C30a3 +C31a2b+C32ab2 +C33 b3
=a3 + 3a2b+3ab2 + b3
= a2 +2ab+b2
展开下面式子
新课讲解
(a+b)2= (a+b) (a+b)
展开后其项的形式为:a2 , ab , b2
这三项的系数为各项在展开式中出现的次数.
考虑b:
每个都不取b的情况有C20 种,则a2前的系数为C20
恰有1个取b的情况有C21种,则ab前的系数为C21
恰有2个取b的情况有C22 种,则b2前的系数为C22
(a+b)2 = a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
对(a+b)2展开式的分析
a3
以 为例体会组合思想
新课讲解
a2b
a2b
a2b
新课讲解
ab2
ab2
ab2
新课讲解
b3
新课讲解
a3
a2b
ab2
b3
新课讲解
a3
新课讲解
a2b
新课讲解
ab2
新课讲解
b3
新课讲解
新课讲解
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
(1)(a+b)4展开后各项形式分别是什么?
(2)各项前的系数代表着什么?
a4 a3b a2b2 ab3 b4
各项前的系数 代表着这些项在展开式中出现的次数
问题
新课讲解
每个都不取b的情况有1种,即C40 ,则a4前的系数为C40
恰有1个取b的情况有C41种,则a3b前的系数为C41
恰有2个取b的情况有C42 种,则a2b2前的系数为C42
恰有3个取b的情况有C43 种,则ab3前的系数为C43
恰有4个取b的情况有C44种,则b4前的系数为C44
则
(a+b)4 =C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(3)你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=
新课讲解
二项式定理
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
新课讲解
右边的多项式叫做(a+b)n的二项展开式
Cnk an-kbk:二项展开式的通项,记作Tk+1
Cnk : 二项式系数
①二项展开式共有n+1项
②各项中a的指数从n起依次减小1,到0为止,
各项中b的指数从0起依次增加1,到n为止.
如(1+x)n = Cn0 + Cn1 x+ Cn2 x2+ … +Cnk xk +…+ xn
注
二项式定理
典型例题
例1
解:
典型例题
例2
求(1+2x)7的展开式的第4项
第4项的二项式系数
第4项的系数
解
(1+2x)7的展开式的第4项是
T3+1=C73 17-3 (2x)3 =35×23×x3 =280x3
第4项的二项式系数是C73 =35
第4项的系数是280
归纳小结
注:(1)注意对二项式定理的灵活应用
(2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
(3)求二项式系数或项的系数的一种方法是将二项式展开
典型例题
例3
(1)第4项;
(2)第4项的二项式系数;
(3)第4项的系数;
(4)含x4项的系数;
(5)常数项;
(6)有理项.
求二项展开式的特定项的常见题型:
①求第k项,Tk=Cnk-1an-k+1bk-1;
②求含xk的项(或 xpyq 的项);
③求常数项;
④求有理项.
方法:根据通项Tk+1=Cnkan-kbk,建立方程求k,再将k的值代回通项求解,注意k的取值范围(k=0,1,2,…,n).
方法归纳
巩固训练
1. 求(x+a)12的展开式中的倒数第4项
解:
(1)(x+a)12的展开式有13项,倒数第4项是它的第10项
归纳小结
1)注意二项式定理中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
例4
(1)(2017·卷1) 展开式中x2的系数为( ) A. 15 B. 20 C. 30 D. 35
多项式乘二项式
典型例题
(2)(2014·卷1) 的展开式中 系数为____.
(3)求 的展开式中的 系数。
求多项式乘二项展开式中的特定项的一般方法:
(1)将多项式中的每一项与二项展开式的通项相乘,得到符合要求的项;
(2)将所有符合要求的项加起来.
方法归纳
例5
(x+y+z)9 中含 x4y2z3 的项的系数是_____
三项式问题
典型例题
典型例题
三项式转化为二项式
解:三项式不能用二项式定理,必须转化为二项式
再利用二项式定理逐项分析常数项得
例6
例7
(2015·卷1) 的展开式中, 系数为____.
典型例题
巩固训练
________
解:
原式化为
其通项公式为
240
括号里含有三项的情况可以把某两项合并为一项,合并时要注意选择的科学性.也可因式分解化为乘积二项式.
求三项展开式中的特定项的一般方法:
(1)利用组合原理,分组计算再求和;
(2)将三项式变成二项式,二次展开.
方法归纳
6.3.1 二项式定理
第二课时
温故知新
1.(a+b)n的二项展开式 是_________.
2.通项公式是 _______________.
Tr+1 =
5.在 展开式中的常数项是____
典型例题
例1、计算:
(1)
(2)
新课讲解
分析:本题的左边是一个数列但不能直接求和.
因为 由此分析求解
两式相加
新课讲解
典型例题
求多项式的展开式中特定的项(系数)
例3
的展开式中, 的系数等于___________
解:仔细观察所给已知条件可直接求得 的系
数是
解法2
运用等比数列求和公式得
在 的展开式中,含有 项的系数为
所以 的系数为-20
求复杂的代数式的展开式中某项(某项的系数),可以逐项分析求解,常常对所给代数式进行化简,可以减小计算量
典型例题
求展开式中系数最大(小)的项
解:
设 项是系数最大的项,则
二项式系数最大的项为第11项,即
所以它们的比是
解决系数最大问题,通常设第 项是系数最大的项,则有
由此确定r的取值
方法总结
变式训练
练习 在 的展开式中,系数绝对值最大的项
解:设系数绝对值最大的项是第r+1项,则
所以当 时,系数绝对值最大的项为
新课讲解
例5:已知a,b∈N,m,n ∈Z ,且2m + n = 0,如果二项式( ax m + bx n )12 的展开式中系数最大的项恰好是常数项,求 a : b 的取值范围。
解:
令m (12 – r )+ nr = 0,将 n =﹣2m 代入,解得 r = 4
故T5 为常数项,且系数最大。
变式训练
2. 已知 的第5项的二项式系数与第3 项的二项式系数比为14:3,求展开式中不含x 的项。
3. 已知 的展开式中,第5项的系数与第3 项的系数比为56:3,求展开式中的常数项。
1. 已知 展开式中第2项大于它的相邻两项,求x的范围。
典型例题
例6 若 展开式中前三项系数成等差数列,
求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。
巩固练习
1. 已知 的展开式中x3的系数
为 ,则常数a的值是_______
2. 在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 207
3. (x+y+z)9中含x4y2z3的项的系数是__________
4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值.
本节课你有哪些收获?请做一下总结!
小结
