6.3.2二项式系数的性质 课件(共32张PPT)-数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.3.2二项式系数的性质 课件(共32张PPT)-数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 21:06:31 | ||
图片预览







文档简介
(共32张PPT)
6.3.2 二项式系数的性质
温故知新
1.二项式定理是什么?二项展开式有哪些基本特征?
共有n+1项;
字母a的最高次数为n且按降幂排列;
字母b的最高次数为n且按升幂排列;
各项中a与b 的指数幂之和都是n ;
各项的二项式系数依次为 ,且与a,b无关.
新课讲解
2.二项展开式的通项是什么?
3.组合数有哪两个基本性质?
新课讲解
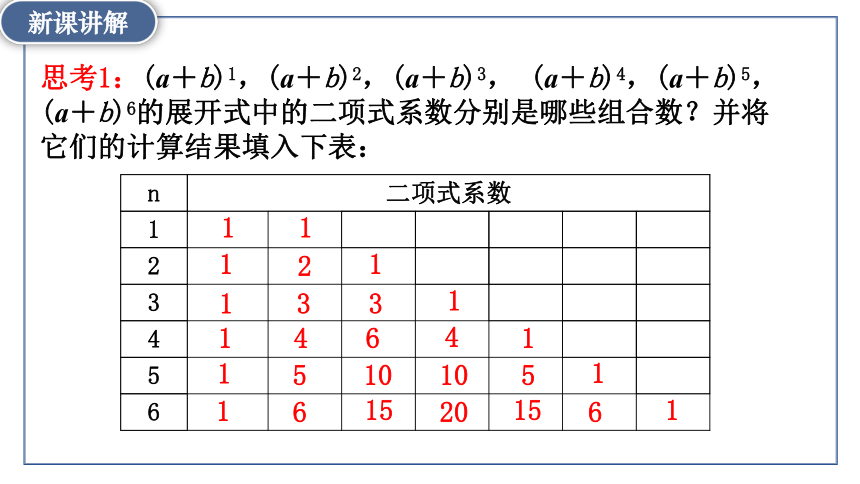
思考1:(a+b)1,(a+b)2,(a+b)3, (a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
6
4
5
10
10
5
6
15
15
20
6
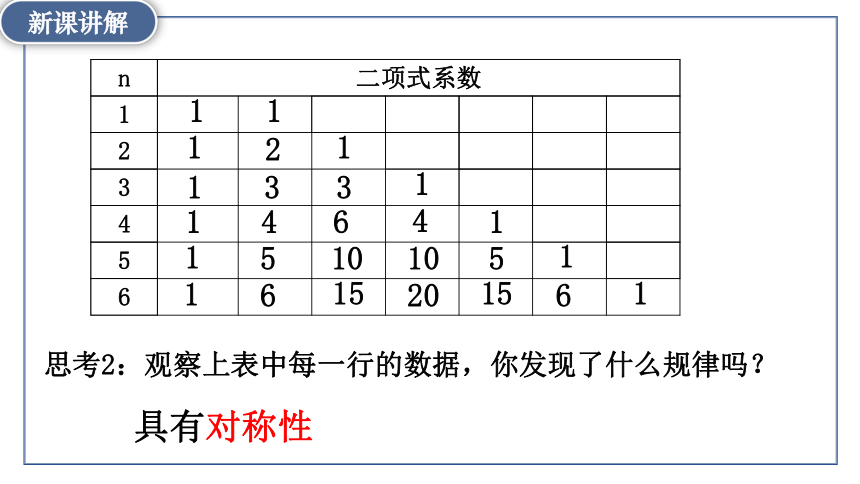
思考2:观察上表中每一行的数据,你发现了什么规律吗?
6
5
4
3
2
1
二项式系数
n
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
6
4
5
10
10
5
6
15
15
20
6
具有对称性
新课讲解
新课讲解
思考3:将上表写成如下形式,你又能发现这些数据有什么新的规律吗?
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6… 1 6 15 20 15 6 1
(1)在同一行中,每行两端都是1,与这两个1等距离的项的系数相等.
(2)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.
新课讲解
思考4:上述数表是我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中最先提出的,是我国古代数学的一个重要成果,比欧洲早五百年左右,我们把这个数表称为杨辉三角,杨辉三角的上述基本性质如何用组合数性质解释?
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6… 1 6 15 20 15 6 1
新课讲解
探究:二项式系数的性质
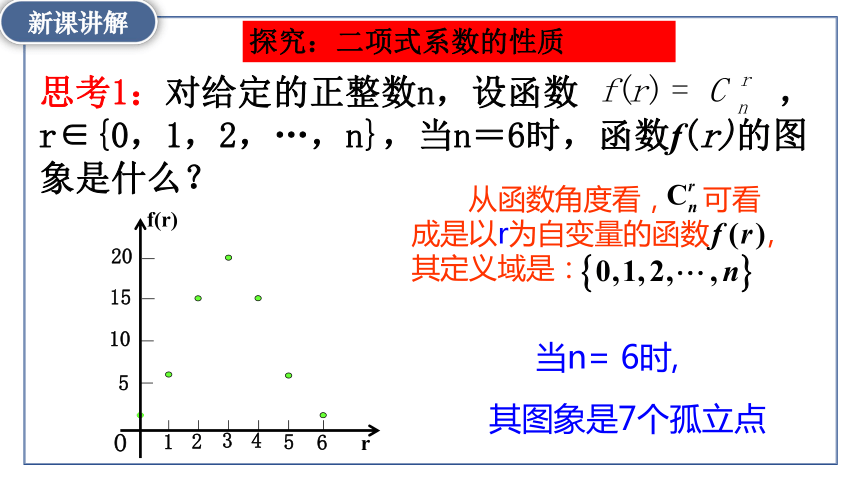
思考1:对给定的正整数n,设函数 ,r∈{0,1,2,…,n},当n=6时,函数f(r)的图象是什么?
r
f(r)
O
1
2
3
4
5
6
5
10
15
20
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是:
当n= 6时,
其图象是7个孤立点
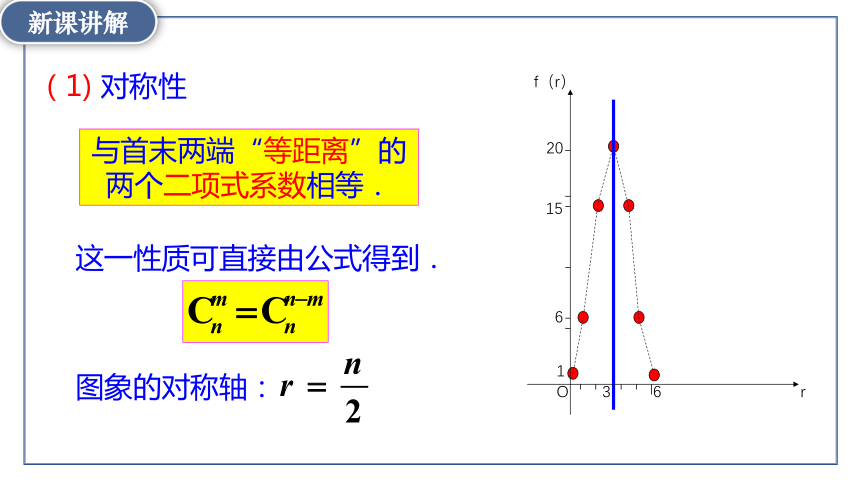
(1) 对称性
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式得到.
图象的对称轴:
f(r)
r
6
3
O
6
15
20
1
新课讲解
(2) 增减性与最大值
所以 相对于 的增减情况由 决定
由:
可知,当 时,
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
新课讲解
f(r)
r
n
O
O
n
f(r)
n为奇数
n为偶数
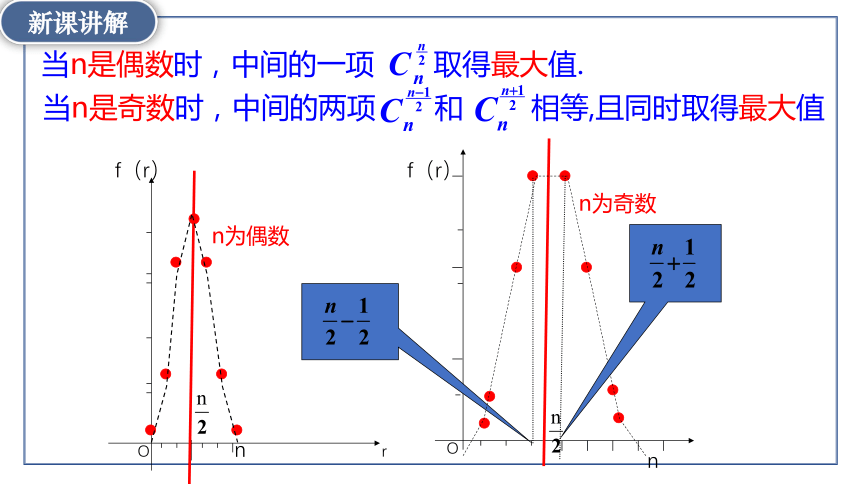
当n是偶数时,中间的一项 取得最大值.
当n是奇数时,中间的两项 和 相等,且同时取得最大值
新课讲解
(3) 各二项式系数的和
在二项式定理中,令 ,则:
这就是说, 的展开式的各二项式系数的和等于
这是组合总数公式.
新课讲解
在二项式定理中,令 ,则:
归纳小结
(1)对称性:与首末两端“等距离”的两个二项式系数相等.
(a+b)n展开式的二项式系数依次是:
(3)增减性与最大值:
增减性的实质是比较 的大小.
(2)递推性: 除1以外的每一个数都 等于它肩上两个数的和.
从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.
(4)各二项式系数的和:
当 时, ;
当 时,
例1. 证明:在(a+b)n 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
在展开式
证明:
得
即
赋值法
中
=2n-1
典型例题
在 展开式中
(1).求二项式系数的和;
例2.
(2).各项系数的和;
(3).奇数项的二项式系数和与偶数项的二项式系数和;
(4).奇数项的系数和与偶数项的系数和.
1024
1
512
典型例题
典型例题
例2、已知(1-2x)7=a0+ a1x + a2x2 + …+ a7x7 ,则
(1) a0 =______; (2) a0+a1+a2+a3+…+a7=____
(3)a1+a3+a5+a7 =____;(4)a0+a2+a4+a6 =______
(5) |a0| + |a1| + |a2| + |a3| +…+ |a7| =____
赋值法
练习:
若已知 (1+2x)200= a0+ a1(x-1) …+ a200(x-1)200
求a1+a3+a5+a7+…+a199 的值。
变式训练
求奇数(次)项偶数(次)项系数的和
(1)
(2)
变式训练
所以
(3)
求二项展开式系数和,常常得用赋值法,设二项式中的字母为1或-1,得到一个或几个等式,再根据结果求值
求奇数(次)项偶数(次)项系数的和
巩固训练
1. 求(3+2x)n 的展开式中各项的系数之和?
令x=1,得各项的系数之和为5n.
2. 已知 , 那么 = ;
4. 在(a+b)20 展开式中,与第五项的系数相同的项是( )
A 第15项 B 第16项 C 第17项 D 第18项
C
3. 若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
5.在(a+b)10展开式中,系数最大的项是( ).
A第6项 B第7项
C第6项和第7项 D第5项和第7项
A
6. 在(a-b)10展开式中,系数最大的项是( ).
A第6项 B第7项
C第6项和第7项 D第5项和第7项
D
巩固训练
7. 已知:(2x+1)10=a0x10+ a1x9+ a2x8+…+a9x+ a10,
(1).求a0+ a1+ a2+…… +a9+ a10的值;
(2).求a0+ a2+ a4+…… + a10的值.
结论:
巩固训练
D
巩固训练
新课讲解
例3 已知(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项.
例4 求集合A={a1,a2,…,an}共有多少个子集?
新课讲解
例5、在(3x -2y)20的展开式中,求:
(1)二项式系数最大的项;(2)系数绝对值最大的项;(3)系数最大的项;
解:(2)设系数绝对值最大的项是第r+1项.则
即 3(r+1)>2(20-r) 得
2(21-r)>3r
所以当r=8时,系数绝对值最大的项为
(3)因为系数为正的项为奇数项,故可设第2r-1项系数最大。
(以下同2)r=5.
归纳小结
1.杨辉三角反映了二项式系数的变化规律,其理论依据是组合数的两个性质.杨辉三角中还有许多有趣性质,可作为一个研究性课题进行探究.
2.二项式系数的性质实质是组合数的一些性质,常作为解决组合数问题的理论依据,但这些性质不能类推到二项展开式的系数.
3.二项式系数的性质:
(1)与首末两端“等距离”的两个二项式系数相等.
(2)二项式系数的前半部分是递增的,后半部分是递减的,且在中间取得最大值.当n为偶数时,正中间一项的二项式系数最大;当n为奇数时,正中间两项的二项式系数相等且为最大.
(3)所有二项式系数之和等于2n,所有奇数项的二项式系数之和与所有偶数项的二项式系数之和相等,且都等于2n-1.
6.3.2 二项式系数的性质
第二课时 应用
典型例题
例1 用二项式定理证明:
(1)251-1能被7整除; (2)5n+1-5(n∈N*)能被20整除.
典型例题
例2 用二项式定理求233除以9的余数.
余数为8
例3 求证: > (n∈N,且n≥2)
证明:
又∵n≥2,上式至少有三项,且
>0
∴ > (n∈N,且n≥2)
典型例题
证明: 要证 成立
只需证 成立
所以原不等式成立
变式训练
1.二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好;
2.注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项;
3.理解和掌握“赋值法”,它是解决有关二项展开式系数的问题的重要手段.
课堂小结
本节课你有哪些收获?请做一下总结!
小结
6.3.2 二项式系数的性质
温故知新
1.二项式定理是什么?二项展开式有哪些基本特征?
共有n+1项;
字母a的最高次数为n且按降幂排列;
字母b的最高次数为n且按升幂排列;
各项中a与b 的指数幂之和都是n ;
各项的二项式系数依次为 ,且与a,b无关.
新课讲解
2.二项展开式的通项是什么?
3.组合数有哪两个基本性质?
新课讲解
思考1:(a+b)1,(a+b)2,(a+b)3, (a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
6
4
5
10
10
5
6
15
15
20
6
思考2:观察上表中每一行的数据,你发现了什么规律吗?
6
5
4
3
2
1
二项式系数
n
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
6
4
5
10
10
5
6
15
15
20
6
具有对称性
新课讲解
新课讲解
思考3:将上表写成如下形式,你又能发现这些数据有什么新的规律吗?
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6… 1 6 15 20 15 6 1
(1)在同一行中,每行两端都是1,与这两个1等距离的项的系数相等.
(2)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和.
新课讲解
思考4:上述数表是我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中最先提出的,是我国古代数学的一个重要成果,比欧洲早五百年左右,我们把这个数表称为杨辉三角,杨辉三角的上述基本性质如何用组合数性质解释?
(a+b)1………………1 1
(a+b)2……………1 2 1
(a+b)3…………1 3 3 1
(a+b)4………1 4 6 4 1
(a+b)5……1 5 10 10 5 1
(a+b)6… 1 6 15 20 15 6 1
新课讲解
探究:二项式系数的性质
思考1:对给定的正整数n,设函数 ,r∈{0,1,2,…,n},当n=6时,函数f(r)的图象是什么?
r
f(r)
O
1
2
3
4
5
6
5
10
15
20
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是:
当n= 6时,
其图象是7个孤立点
(1) 对称性
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式得到.
图象的对称轴:
f(r)
r
6
3
O
6
15
20
1
新课讲解
(2) 增减性与最大值
所以 相对于 的增减情况由 决定
由:
可知,当 时,
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值
新课讲解
f(r)
r
n
O
O
n
f(r)
n为奇数
n为偶数
当n是偶数时,中间的一项 取得最大值.
当n是奇数时,中间的两项 和 相等,且同时取得最大值
新课讲解
(3) 各二项式系数的和
在二项式定理中,令 ,则:
这就是说, 的展开式的各二项式系数的和等于
这是组合总数公式.
新课讲解
在二项式定理中,令 ,则:
归纳小结
(1)对称性:与首末两端“等距离”的两个二项式系数相等.
(a+b)n展开式的二项式系数依次是:
(3)增减性与最大值:
增减性的实质是比较 的大小.
(2)递推性: 除1以外的每一个数都 等于它肩上两个数的和.
从第一项起至中间项,二项式系数逐渐增大,随后又逐渐减小.
(4)各二项式系数的和:
当 时, ;
当 时,
例1. 证明:在(a+b)n 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
在展开式
证明:
得
即
赋值法
中
=2n-1
典型例题
在 展开式中
(1).求二项式系数的和;
例2.
(2).各项系数的和;
(3).奇数项的二项式系数和与偶数项的二项式系数和;
(4).奇数项的系数和与偶数项的系数和.
1024
1
512
典型例题
典型例题
例2、已知(1-2x)7=a0+ a1x + a2x2 + …+ a7x7 ,则
(1) a0 =______; (2) a0+a1+a2+a3+…+a7=____
(3)a1+a3+a5+a7 =____;(4)a0+a2+a4+a6 =______
(5) |a0| + |a1| + |a2| + |a3| +…+ |a7| =____
赋值法
练习:
若已知 (1+2x)200= a0+ a1(x-1) …+ a200(x-1)200
求a1+a3+a5+a7+…+a199 的值。
变式训练
求奇数(次)项偶数(次)项系数的和
(1)
(2)
变式训练
所以
(3)
求二项展开式系数和,常常得用赋值法,设二项式中的字母为1或-1,得到一个或几个等式,再根据结果求值
求奇数(次)项偶数(次)项系数的和
巩固训练
1. 求(3+2x)n 的展开式中各项的系数之和?
令x=1,得各项的系数之和为5n.
2. 已知 , 那么 = ;
4. 在(a+b)20 展开式中,与第五项的系数相同的项是( )
A 第15项 B 第16项 C 第17项 D 第18项
C
3. 若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
5.在(a+b)10展开式中,系数最大的项是( ).
A第6项 B第7项
C第6项和第7项 D第5项和第7项
A
6. 在(a-b)10展开式中,系数最大的项是( ).
A第6项 B第7项
C第6项和第7项 D第5项和第7项
D
巩固训练
7. 已知:(2x+1)10=a0x10+ a1x9+ a2x8+…+a9x+ a10,
(1).求a0+ a1+ a2+…… +a9+ a10的值;
(2).求a0+ a2+ a4+…… + a10的值.
结论:
巩固训练
D
巩固训练
新课讲解
例3 已知(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项.
例4 求集合A={a1,a2,…,an}共有多少个子集?
新课讲解
例5、在(3x -2y)20的展开式中,求:
(1)二项式系数最大的项;(2)系数绝对值最大的项;(3)系数最大的项;
解:(2)设系数绝对值最大的项是第r+1项.则
即 3(r+1)>2(20-r) 得
2(21-r)>3r
所以当r=8时,系数绝对值最大的项为
(3)因为系数为正的项为奇数项,故可设第2r-1项系数最大。
(以下同2)r=5.
归纳小结
1.杨辉三角反映了二项式系数的变化规律,其理论依据是组合数的两个性质.杨辉三角中还有许多有趣性质,可作为一个研究性课题进行探究.
2.二项式系数的性质实质是组合数的一些性质,常作为解决组合数问题的理论依据,但这些性质不能类推到二项展开式的系数.
3.二项式系数的性质:
(1)与首末两端“等距离”的两个二项式系数相等.
(2)二项式系数的前半部分是递增的,后半部分是递减的,且在中间取得最大值.当n为偶数时,正中间一项的二项式系数最大;当n为奇数时,正中间两项的二项式系数相等且为最大.
(3)所有二项式系数之和等于2n,所有奇数项的二项式系数之和与所有偶数项的二项式系数之和相等,且都等于2n-1.
6.3.2 二项式系数的性质
第二课时 应用
典型例题
例1 用二项式定理证明:
(1)251-1能被7整除; (2)5n+1-5(n∈N*)能被20整除.
典型例题
例2 用二项式定理求233除以9的余数.
余数为8
例3 求证: > (n∈N,且n≥2)
证明:
又∵n≥2,上式至少有三项,且
>0
∴ > (n∈N,且n≥2)
典型例题
证明: 要证 成立
只需证 成立
所以原不等式成立
变式训练
1.二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好;
2.注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项;
3.理解和掌握“赋值法”,它是解决有关二项展开式系数的问题的重要手段.
课堂小结
本节课你有哪些收获?请做一下总结!
小结
