6.2.1排列、6.2.2排列数 课件(共51张PPT)-数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 6.2.1排列、6.2.2排列数 课件(共51张PPT)-数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 21:09:43 | ||
图片预览










文档简介
(共51张PPT)
6.2.1 排列
复习回顾
分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 ……在第n类方案中有mn种不同的方法.那么完成这件事共有
种不同的方法.
分步乘法计数原理:
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……,做第n步有mn种不同的方法.那么完成这件事共有 种不同的方法.
课堂探究
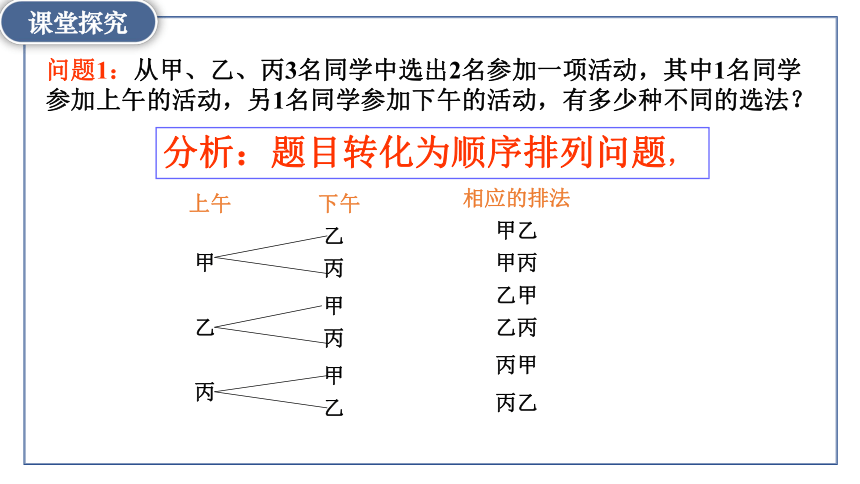
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
分析:题目转化为顺序排列问题,
新课讲解
把上面问题中被取的对象叫做元素,于是问题1就可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
ab, ac, ba, bc, ca, cb
新课讲解
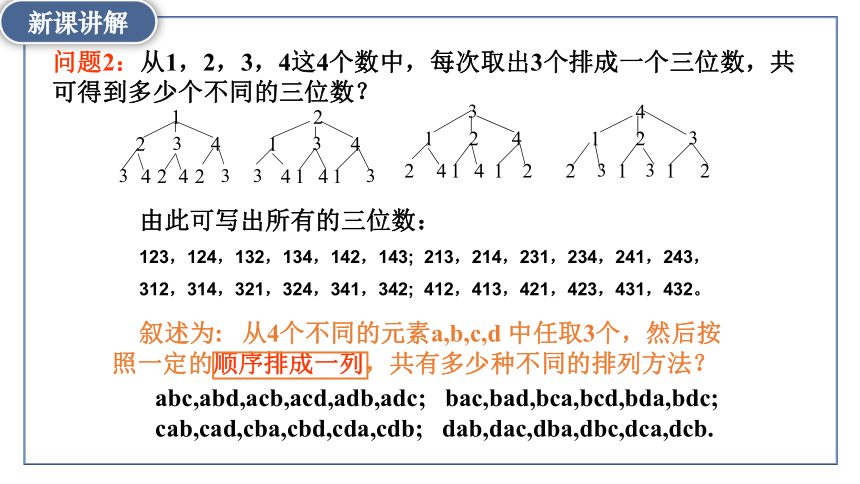
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
叙述为: 从4个不同的元素a,b,c,d 中任取3个,然后按 照一定的顺序排成一列,共有多少种不同的排列方法?
abc,abd,acb,acd,adb,adc; bac,bad,bca,bcd,bda,bdc;
cab,cad,cba,cbd,cda,cdb; dab,dac,dba,dbc,dca,dcb.
由此可写出所有的三位数:
123,124,132,134,142,143; 213,214,231,234,241,243,
312,314,321,324,341,342; 412,413,421,423,431,432。
新课讲解
问题1
从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同的排法
实质是:从3个不同的元素中,任取2个,按一定的顺序排成一列,有哪些不同的排法?
问题2
从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
实质是:从4个不同的元素中, 任取3个,按照一定的顺序排成一列,写出所有不同的排法.
定义:一般地说,从n个不同的元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列.
新课讲解
1、排列:
从n个不同元素中取出m (m n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
说明:
1、元素不能重复。
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为使写出的所有排列情况既不重复也不遗漏,可采用“树形图”。
(有序性)
(互异性)
概念辨析
练习1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条射线?可确定多少条直线?
(5)10个学生排队照相,则不同的站法有多少种?
(从中归纳这几类问题的区别)
是排列
不是排列
是排列
是排列
不是排列
是排列
新课讲解
练习3.写出从5个元素a,b,c,d,e中任取2个元素的所有排列.
解决办法是先画“树形图”,再由此写出所有的排列,共20个.
若把这题改为:写出从5个元素a,b,c,d,e中任取3个元素的所有排列,结果如何呢?
方法仍然照用,但数字将更大,写起来更“啰嗦”.
练习2.在A、B、C、D四位候选人中,选举正、副班长各一人,共有几种不同的选法?写出所有可能的选举结果.
AB AC AD BA BC BD CA CB CD DA DB DC
研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?我们将来共同探讨这个问题:排列数及其公式.
6.2.2 排列数
新课讲解
2、排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,不是数;
个元素
新课讲解
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
新课讲解
(1)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
(2)排列数公式(2):
说明:
1、排列数公式的第一个常用来计算,第二个常用来证明。
为了使当m=n时上面的公式也成立,规定:
2、对于 这个条件要留意,往往是解方程时的隐含条件。
新课讲解
排列数公式:
常用于计算含有数字的排列数的值
常用于对含有字母的排列数的式子进行变形和论证
课堂小结
【排列】从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列.
【关键点】1、互异性(被选、所选元素互不相同)
2、有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列总数
典型例题
例1 计算:
=6!=6×5×4×3×2×1=720
变式训练
17
14
n(n-1)=90
10
3.由乘积式写出排列数的符号
(m-2)(m-3)…….(m-k+3)
典型例题
例2.解方程:
(1)n=3 (2)m=6
典型例题
例3 求证下列各式:
你能用学过的方法,举一实际的例子说明(1)、(2)吗?
变式训练
求证:1!+2·2!+3·3!+…+n·n!=(n+1)!- 1
分析:n·n!=(n+1)!-n!
证明:∵n·n!=(n+1)!-n!
左边=
注意阶乘的几种变形
课堂小结
1.排列的定义;(不同元素)
2.排列数公式;
3.几种阶乘变形.
6.2.1 排列
第二课时 排列的应用
复习回顾
1.排列的定义,理解排列定义需要注意的几点问题;
从n个不同元素中,任取m(m2.排列数的定义,排列数的计算公式
典型例题
例1. 某段铁路上有12个车站,共需要准备多少种普通客票?
一、无限制条件的排列问题
例2、某年全国足球甲级(A组)联赛共有14队参加,每队都要与其余各队在主客场分别比赛1次,共进行多少场比赛
变式训练
1.从5种不同的蔬菜种子中选3种分别种在3块不同土质的土地上,共有多少种不同的种法?
分析:把5个种子分别标上1,2,3,4,5,用123表示种子1种在第1块土地上,种子2种在第2块土地上,种子3种在第3块土地上,因此3个数的一个排列就是一种种植方法,从5个不同数中取出3个数的一个排列就是一种种植方法,多少个排列就有多少种种法。
变式训练
2.公共汽车上有4位乘客,其中任何两个人都不在同一车站下车,汽车沿途停靠6个站,那么这4位乘客不同的下车方法有多少种?
分析:6个车站分别标上1,2,3,4,5,6,如1246表示第一位乘客在1号站下,第二位乘客在2号站下,第三位乘客在4号站下,第四位乘客在6号车站下,不同的排列表示不同的下法,有多少个不同的排列就有多少种不同的下法,共有A46=6·5·4·3=360
变式训练
3、有5名男生,4名女生排队。
(1)从中选出3人排成一排,有多少种排法?
(2)全部排成一排,有有多少种排法?
(3)排成两排,前排4人,后排5人,有多少种排法?
典型例题
例3 某信号共用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
变式:将题中的“3面旗”改为“3色旗”,结论如何?
变式训练
1、20位同学互通一封信,那么通信次数是多少?
2、由数字1、2、3、4、5、6可以组成多少个没有重复数字的正整数?
3、5个班,有5名语文老师、5名数学老师、5名英语老师,每个班上配一名语文老师、一名数学老师和一名英语老师,问有多少种不同的搭配方法?
新课讲解
例4 用0到9这十个数字,可以组成多少个没有重复数字的三位数?
分析1:由于百位上的数字不能为0,只能从1到9这9个数字中任选一个,有 种选法,再排十位和个位上的数字,可以从余下的9个数字中任选2个,有 种选法,根据分步计数原理,所求三位数的个数是:
分析2:所求的三位数可分为:不含数字0的,有 个;含有数字0的,有 个,根据分类计数原理,所求三位数的个数是:
分析3:从0到9这十个数字中取3个的排列数为 ,其中以0为百位数字的排列数为 ,故所求三位数的个数是:
(特殊位置预置法)
(特殊元素预置法)
(排除法)
二、有限制条件的排列问题
归纳总结
小 结一:对于“在”与“不在”等有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优限法)。
优限法
变式训练
变:1、用0到9这十个数字,可以组成多少个没有重复数字的且能被5整除的三位数?
2、用1到9这九个数字,可以组成多少个没有重复数字的且能被3整除的三位数?
典型例题
例5 5个人站成一排
⑴共有多少种排法?
⑵其中甲必须站在中间,有多少种不同的排法?
⑶其中甲、乙两人必须相邻,有多少种不同的排法?
⑷其中甲、乙两人不相邻,有多少种不同的排法?
⑸其中甲、乙两人不站排头和排尾,有多少种不同的排法?
⑹其中甲不站排头,乙不站排尾,有多少种不同的排法?
归纳小结
小结二:对于相邻问题,常用“捆绑法”(先捆后松).
捆绑法
小结三:对于不相邻问题,常用“插空法”(特殊元素后考虑).
插空法
例5 5个人站成一排
⑸其中甲、乙两人不站排头和排尾,有多少种不同的排法?
解:⑸ 甲、乙两人不站排头和排尾,则这两个位置可从其余3人中选2人来站,有 种排法,剩下的人有 种排法,共有 种排法.
(特殊位置预置法)
(特殊元素预置法)
(排除法)
典型例题
典型例题
例5 5个人站成一排
⑹其中甲不站排头,乙不站排尾,有多少种不同的排法?
解:⑹ 甲站排头有 种排法,乙站排尾有 种排法,但两种情况都包含了“甲站排头,乙站排尾”的情况,有 种排法,所以共有 种排法.
用直接法,如何分类?
一类:甲站排尾
二类:甲站中间
所以共有 种排法.
典型例题
(7)、甲与乙中间必须排2名,有几种排法?
例5 5个人站成一排
典型例题
例6 有4名男生,3名女生。3名女生高矮互不等,将7名学生排成一行,要求从左到右,女生从矮到高排列,有多少种排法?
顺序固定问题用“除法”
对于某几个元素顺序一定的排列问题,可先将这几个元素与其它元素一同进行排列,然后用总的排列数除以这几个元素的全排列数.
所以共有 种。
分析:先在7个位置上作全排列,有 种排法。其中3个女生因要求“从矮到高”排,只有一种顺序故 只对应一种排法,
典型例题
本题也可以这样考虑:对应于先将没有限制条件的其他元素进行排列,有 种方法;
再将有限制条件(顺序要求)的元素进行排列,只有一种方法;
故,总的排列方法数为:
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(1)若其中的A小孩必须站在B小孩的左边,有多少种不同的排法?
解1:A在B左边的一种排法必对应着A在B右边的一种排法,所以在全排列中, A在B左边与A在B右边的排法数相等,因此有:
排法。
(种)
2520
5
7
=
A
解法2
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
2)若三个女孩要站在一起,有多少种不同的排法?
解:将三个女孩看作一人与四个男孩排队,有 种排法,而三个女孩之间有 种排法,所以不同的排法共有: (种)。
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(3)若三个女孩要站在一起,四个男孩也 要站在一起,有多少种不同的排法?
不同的排法有:
(种)
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(4)若三个女孩互不相邻,有多少种不同的排法?
解:先把四个男孩排成一排有 种排法,在每一排列中有五个空档(包括两端),再把三个女孩插入空档中有 种方法,所以共有: (种)排法。
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(5)若三个女孩互不相邻,四个男孩也互不相邻,有多少种不同的排法?
不同的排法共有:
(种)
相
间
问
题
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成两排照相留念。
(6)若前排站三人,后排站四人,其中的A.B两小孩必须站前排且相邻,有多少种不同的排法?
解:A,B两小孩的站法有: (种),其余人的站法有 (种),所以共有 (种) 排法。
变式训练
解:连续命中的3枪和命中的另一枪被未命中的4枪所隔开 ,如图 表示没有命中,
_ _ _ _ _
命中的三枪看作一个元素和另外命中的一枪共两个元素插到五个空档中有A25=5·4=20种排法
2.某人射击8枪,命中4枪,4枪命中恰好3枪连在一起的不同种数有多少?
变式训练
1、4个学生和3个老师排成一排照相,老师不能排两端,且老师必须排在一起的不同排法种数是( )
A . B . C . D .
2、停车场上有一排七个停车位,现有四辆汽车要停放,若要使三个空位连在一起,则停放的方法有 种.
3、用0、1、2、3、4、5六个数字,可组成多少个无重复数字且不能被5整除的五位数?
4、在7名运动员中选出4名组成接力队,参加4×100米接力赛,那么甲、乙两人都不跑中间两棒的安排方法有多少种?
D
法一:
法二:
拓展训练
1、把15个人分成前后三排,每排5人,不同的排法数为( )
2、计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画,排成一行陈列,要求同一品种的画必须连在一起,那么不同的陈列方式有( )
3、由1、2、3、4、5这5个数字组成无重复数字的五位数,其中
奇数有 个.
C
B
拓展训练
4、某城市在中心广场建造一个花圃,花圃分为6个部分(如右图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有______种.(以数字作答)
所以,共有48+48+24=120种.
解法:从题意来看6部分种4种颜色的花,又从图形看 知必有2组同颜色的花,从同颜色的花入手分类求
(2)③与⑤同色,则②④或⑥④同色,所以共有
=48种;
(3)②与④且③与⑥同色,则共 =24种
(1)②与⑤同色,则③⑥也同色或④⑥也同色,所以共有
=48种;
课堂小结
从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数
当两个排列的元素完全相同,且元素的排列顺序相同称两个排列相同
An =n(n-1)(n-2) …(n-m+1)
m
m≤n
规定0!=1
本节课你有哪些收获?请做一下总结!
小结
6.2.1 排列
复习回顾
分类加法计数原理:
完成一件事,有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法 ……在第n类方案中有mn种不同的方法.那么完成这件事共有
种不同的方法.
分步乘法计数原理:
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……,做第n步有mn种不同的方法.那么完成这件事共有 种不同的方法.
课堂探究
上午
下午
相应的排法
甲
乙
丙
乙
甲
丙
丙
甲
乙
甲丙
甲乙
乙甲
乙丙
丙甲
丙乙
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的选法?
分析:题目转化为顺序排列问题,
新课讲解
把上面问题中被取的对象叫做元素,于是问题1就可以叙述为:
从3个不同的元素a,b,c中任取2个,然后按照一定的顺序排成一列,一共有多少种不同的排列方法?
ab, ac, ba, bc, ca, cb
新课讲解
问题2:从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
叙述为: 从4个不同的元素a,b,c,d 中任取3个,然后按 照一定的顺序排成一列,共有多少种不同的排列方法?
abc,abd,acb,acd,adb,adc; bac,bad,bca,bcd,bda,bdc;
cab,cad,cba,cbd,cda,cdb; dab,dac,dba,dbc,dca,dcb.
由此可写出所有的三位数:
123,124,132,134,142,143; 213,214,231,234,241,243,
312,314,321,324,341,342; 412,413,421,423,431,432。
新课讲解
问题1
从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名参加上午的活动,1名参加下午的活动,有哪些不同的排法
实质是:从3个不同的元素中,任取2个,按一定的顺序排成一列,有哪些不同的排法?
问题2
从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
实质是:从4个不同的元素中, 任取3个,按照一定的顺序排成一列,写出所有不同的排法.
定义:一般地说,从n个不同的元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列.
新课讲解
1、排列:
从n个不同元素中取出m (m n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
说明:
1、元素不能重复。
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为使写出的所有排列情况既不重复也不遗漏,可采用“树形图”。
(有序性)
(互异性)
概念辨析
练习1 下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条射线?可确定多少条直线?
(5)10个学生排队照相,则不同的站法有多少种?
(从中归纳这几类问题的区别)
是排列
不是排列
是排列
是排列
不是排列
是排列
新课讲解
练习3.写出从5个元素a,b,c,d,e中任取2个元素的所有排列.
解决办法是先画“树形图”,再由此写出所有的排列,共20个.
若把这题改为:写出从5个元素a,b,c,d,e中任取3个元素的所有排列,结果如何呢?
方法仍然照用,但数字将更大,写起来更“啰嗦”.
练习2.在A、B、C、D四位候选人中,选举正、副班长各一人,共有几种不同的选法?写出所有可能的选举结果.
AB AC AD BA BC BD CA CB CD DA DB DC
研究一个排列问题,往往只需知道所有排列的个数而无需一一写出所有的排列,那么能否不通过一一写出所有的排列而直接“得”出所有排列的个数呢?我们将来共同探讨这个问题:排列数及其公式.
6.2.2 排列数
新课讲解
2、排列数:
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,不是数;
个元素
新课讲解
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
新课讲解
(1)排列数公式(1):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
(2)排列数公式(2):
说明:
1、排列数公式的第一个常用来计算,第二个常用来证明。
为了使当m=n时上面的公式也成立,规定:
2、对于 这个条件要留意,往往是解方程时的隐含条件。
新课讲解
排列数公式:
常用于计算含有数字的排列数的值
常用于对含有字母的排列数的式子进行变形和论证
课堂小结
【排列】从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列.
【关键点】1、互异性(被选、所选元素互不相同)
2、有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列总数
典型例题
例1 计算:
=6!=6×5×4×3×2×1=720
变式训练
17
14
n(n-1)=90
10
3.由乘积式写出排列数的符号
(m-2)(m-3)…….(m-k+3)
典型例题
例2.解方程:
(1)n=3 (2)m=6
典型例题
例3 求证下列各式:
你能用学过的方法,举一实际的例子说明(1)、(2)吗?
变式训练
求证:1!+2·2!+3·3!+…+n·n!=(n+1)!- 1
分析:n·n!=(n+1)!-n!
证明:∵n·n!=(n+1)!-n!
左边=
注意阶乘的几种变形
课堂小结
1.排列的定义;(不同元素)
2.排列数公式;
3.几种阶乘变形.
6.2.1 排列
第二课时 排列的应用
复习回顾
1.排列的定义,理解排列定义需要注意的几点问题;
从n个不同元素中,任取m(m
典型例题
例1. 某段铁路上有12个车站,共需要准备多少种普通客票?
一、无限制条件的排列问题
例2、某年全国足球甲级(A组)联赛共有14队参加,每队都要与其余各队在主客场分别比赛1次,共进行多少场比赛
变式训练
1.从5种不同的蔬菜种子中选3种分别种在3块不同土质的土地上,共有多少种不同的种法?
分析:把5个种子分别标上1,2,3,4,5,用123表示种子1种在第1块土地上,种子2种在第2块土地上,种子3种在第3块土地上,因此3个数的一个排列就是一种种植方法,从5个不同数中取出3个数的一个排列就是一种种植方法,多少个排列就有多少种种法。
变式训练
2.公共汽车上有4位乘客,其中任何两个人都不在同一车站下车,汽车沿途停靠6个站,那么这4位乘客不同的下车方法有多少种?
分析:6个车站分别标上1,2,3,4,5,6,如1246表示第一位乘客在1号站下,第二位乘客在2号站下,第三位乘客在4号站下,第四位乘客在6号车站下,不同的排列表示不同的下法,有多少个不同的排列就有多少种不同的下法,共有A46=6·5·4·3=360
变式训练
3、有5名男生,4名女生排队。
(1)从中选出3人排成一排,有多少种排法?
(2)全部排成一排,有有多少种排法?
(3)排成两排,前排4人,后排5人,有多少种排法?
典型例题
例3 某信号共用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
变式:将题中的“3面旗”改为“3色旗”,结论如何?
变式训练
1、20位同学互通一封信,那么通信次数是多少?
2、由数字1、2、3、4、5、6可以组成多少个没有重复数字的正整数?
3、5个班,有5名语文老师、5名数学老师、5名英语老师,每个班上配一名语文老师、一名数学老师和一名英语老师,问有多少种不同的搭配方法?
新课讲解
例4 用0到9这十个数字,可以组成多少个没有重复数字的三位数?
分析1:由于百位上的数字不能为0,只能从1到9这9个数字中任选一个,有 种选法,再排十位和个位上的数字,可以从余下的9个数字中任选2个,有 种选法,根据分步计数原理,所求三位数的个数是:
分析2:所求的三位数可分为:不含数字0的,有 个;含有数字0的,有 个,根据分类计数原理,所求三位数的个数是:
分析3:从0到9这十个数字中取3个的排列数为 ,其中以0为百位数字的排列数为 ,故所求三位数的个数是:
(特殊位置预置法)
(特殊元素预置法)
(排除法)
二、有限制条件的排列问题
归纳总结
小 结一:对于“在”与“不在”等有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优限法)。
优限法
变式训练
变:1、用0到9这十个数字,可以组成多少个没有重复数字的且能被5整除的三位数?
2、用1到9这九个数字,可以组成多少个没有重复数字的且能被3整除的三位数?
典型例题
例5 5个人站成一排
⑴共有多少种排法?
⑵其中甲必须站在中间,有多少种不同的排法?
⑶其中甲、乙两人必须相邻,有多少种不同的排法?
⑷其中甲、乙两人不相邻,有多少种不同的排法?
⑸其中甲、乙两人不站排头和排尾,有多少种不同的排法?
⑹其中甲不站排头,乙不站排尾,有多少种不同的排法?
归纳小结
小结二:对于相邻问题,常用“捆绑法”(先捆后松).
捆绑法
小结三:对于不相邻问题,常用“插空法”(特殊元素后考虑).
插空法
例5 5个人站成一排
⑸其中甲、乙两人不站排头和排尾,有多少种不同的排法?
解:⑸ 甲、乙两人不站排头和排尾,则这两个位置可从其余3人中选2人来站,有 种排法,剩下的人有 种排法,共有 种排法.
(特殊位置预置法)
(特殊元素预置法)
(排除法)
典型例题
典型例题
例5 5个人站成一排
⑹其中甲不站排头,乙不站排尾,有多少种不同的排法?
解:⑹ 甲站排头有 种排法,乙站排尾有 种排法,但两种情况都包含了“甲站排头,乙站排尾”的情况,有 种排法,所以共有 种排法.
用直接法,如何分类?
一类:甲站排尾
二类:甲站中间
所以共有 种排法.
典型例题
(7)、甲与乙中间必须排2名,有几种排法?
例5 5个人站成一排
典型例题
例6 有4名男生,3名女生。3名女生高矮互不等,将7名学生排成一行,要求从左到右,女生从矮到高排列,有多少种排法?
顺序固定问题用“除法”
对于某几个元素顺序一定的排列问题,可先将这几个元素与其它元素一同进行排列,然后用总的排列数除以这几个元素的全排列数.
所以共有 种。
分析:先在7个位置上作全排列,有 种排法。其中3个女生因要求“从矮到高”排,只有一种顺序故 只对应一种排法,
典型例题
本题也可以这样考虑:对应于先将没有限制条件的其他元素进行排列,有 种方法;
再将有限制条件(顺序要求)的元素进行排列,只有一种方法;
故,总的排列方法数为:
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(1)若其中的A小孩必须站在B小孩的左边,有多少种不同的排法?
解1:A在B左边的一种排法必对应着A在B右边的一种排法,所以在全排列中, A在B左边与A在B右边的排法数相等,因此有:
排法。
(种)
2520
5
7
=
A
解法2
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
2)若三个女孩要站在一起,有多少种不同的排法?
解:将三个女孩看作一人与四个男孩排队,有 种排法,而三个女孩之间有 种排法,所以不同的排法共有: (种)。
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(3)若三个女孩要站在一起,四个男孩也 要站在一起,有多少种不同的排法?
不同的排法有:
(种)
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(4)若三个女孩互不相邻,有多少种不同的排法?
解:先把四个男孩排成一排有 种排法,在每一排列中有五个空档(包括两端),再把三个女孩插入空档中有 种方法,所以共有: (种)排法。
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成一排照相留念。
(5)若三个女孩互不相邻,四个男孩也互不相邻,有多少种不同的排法?
不同的排法共有:
(种)
相
间
问
题
变式训练
1.七个家庭一起外出旅游,若其中四家是男孩,三家是女孩,现将这七个小孩站成两排照相留念。
(6)若前排站三人,后排站四人,其中的A.B两小孩必须站前排且相邻,有多少种不同的排法?
解:A,B两小孩的站法有: (种),其余人的站法有 (种),所以共有 (种) 排法。
变式训练
解:连续命中的3枪和命中的另一枪被未命中的4枪所隔开 ,如图 表示没有命中,
_ _ _ _ _
命中的三枪看作一个元素和另外命中的一枪共两个元素插到五个空档中有A25=5·4=20种排法
2.某人射击8枪,命中4枪,4枪命中恰好3枪连在一起的不同种数有多少?
变式训练
1、4个学生和3个老师排成一排照相,老师不能排两端,且老师必须排在一起的不同排法种数是( )
A . B . C . D .
2、停车场上有一排七个停车位,现有四辆汽车要停放,若要使三个空位连在一起,则停放的方法有 种.
3、用0、1、2、3、4、5六个数字,可组成多少个无重复数字且不能被5整除的五位数?
4、在7名运动员中选出4名组成接力队,参加4×100米接力赛,那么甲、乙两人都不跑中间两棒的安排方法有多少种?
D
法一:
法二:
拓展训练
1、把15个人分成前后三排,每排5人,不同的排法数为( )
2、计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画,排成一行陈列,要求同一品种的画必须连在一起,那么不同的陈列方式有( )
3、由1、2、3、4、5这5个数字组成无重复数字的五位数,其中
奇数有 个.
C
B
拓展训练
4、某城市在中心广场建造一个花圃,花圃分为6个部分(如右图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有______种.(以数字作答)
所以,共有48+48+24=120种.
解法:从题意来看6部分种4种颜色的花,又从图形看 知必有2组同颜色的花,从同颜色的花入手分类求
(2)③与⑤同色,则②④或⑥④同色,所以共有
=48种;
(3)②与④且③与⑥同色,则共 =24种
(1)②与⑤同色,则③⑥也同色或④⑥也同色,所以共有
=48种;
课堂小结
从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列
从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数
当两个排列的元素完全相同,且元素的排列顺序相同称两个排列相同
An =n(n-1)(n-2) …(n-m+1)
m
m≤n
规定0!=1
本节课你有哪些收获?请做一下总结!
小结
