7.4.2 超几何分布 课件(共56张PPT)-数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.4.2 超几何分布 课件(共56张PPT)-数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 21:13:39 | ||
图片预览










文档简介
(共56张PPT)
7.4.2 超几何分布
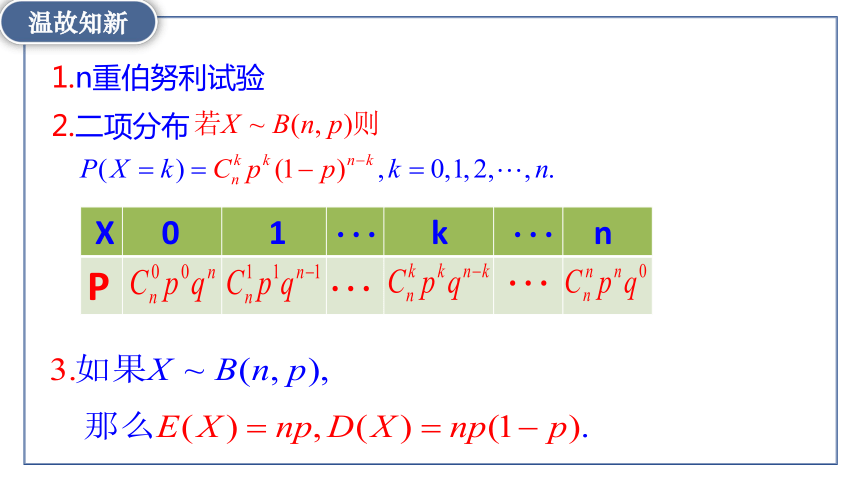
温故知新
2.二项分布
X 0 1 k n
P
1.n重伯努利试验
新课讲解
超几何分布
一般地,假设一批产品共有N件,其中有M件次品. 从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
如果随机变量X的分布列具有上式的形式,
那么称随机变量X服从超几何分布.
新课讲解
超几何分布
1.公式中个字母的含义
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
2.求分布列时可以直接利用组合数的意义列式计算,不必机械记忆这个概率分布列.
3. “任取n件,恰有z件次品”是一次性抽取,用组合数列式.
4.各对应的概率和必须为1.
典型例题
解:
例4.从50名学生中随机选出5名学生代表,求甲被选中的概率.
设X表示选出的5名数学中含甲的人数(只能取0或1),
则X服从超几何分布,
且N=50,M=1,n=5,
因此甲被选中的概率为
方法归纳
1.判断随机变量是否服从超几何分布;
2.根据已知条件,确定M,N,n对应的值;
3.代入超几何分布的概率公式,求出结果;
超几何分布的使用步骤:
典型例题
解:
另解:
例5. 一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检
测,求至少有1件不合格的概率.
巩固训练
1.学校要从12名候选人中选4名同学组成学生会,已知有4名候选人来自甲班.假设每名候选人都有相同的机会被选到,
(1)求甲班恰有2名同学被选到的概率.
(2)求甲班至多1名同学被选到的概率
解:
(1)设甲班恰有X人被选到,
则X服从超几何分布,
且N=12,M=4,n=4,
(2)
巩固训练
解:
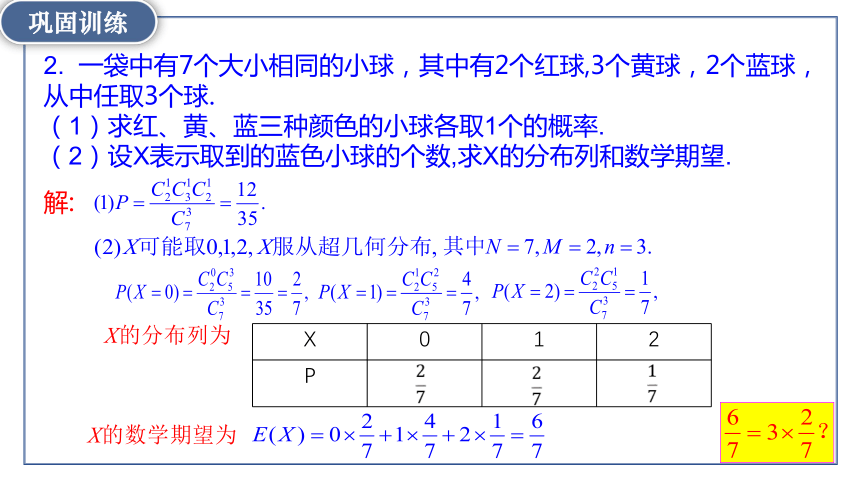
2. 一袋中有7个大小相同的小球,其中有2个红球,3个黄球,2个蓝球,从中任取3个球.
(1)求红、黄、蓝三种颜色的小球各取1个的概率.
(2)设X表示取到的蓝色小球的个数,求X的分布列和数学期望.
X 0 1 2
P
课堂探究
探究: 服从超几何分布的随机变量的均值是什么
新课讲解
超几何分布的均值
若X服从超几何分布,
典型例题
解:
例6.一袋中有100个大小相同的小球,其中有40个黄球,60个白球,从中随机摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回和不放回摸球,求X的分布列;
(2)分别就有放回和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
新课讲解
解(2)
采用不放回摸球估算的结果更可靠些
新课讲解
0.05
0
0.10
0.15
0.20
0.25
两种摸球方式下,随机变量X服从二项分布和超几何分布.
这两种分布的均值相等都等于8.
但从两种分步的概率分步图看,超几何分布更集中在均值附近.
当n远远小于N时,每次抽取一次,对N的影响很小.
此时,超几何分布可以用二项分步近似.
辨析
二项分布与超几何分布区别和联系
1.区别
一般地,超几何分布的模型是“取次品”是不放回抽样,
而二项分布的模型是“独立重复试验”对于抽样,则是有放回抽样.
2.联系
当次品的数量充分大,且抽取的数量较小时,即便是不放回抽样,也可视其为二项分布.
巩固训练
1. PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的可入肺颗粒物,根据现行国家标 准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2018年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
PM2.5日均值(微克/立方米) [25,35) [35,45) [45,55) [55,65) [65,75) [75,85]
频数 3 1 1 1 1 3
(1)从这10天的PM2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ 的分布列.
新课讲解
X 0 1 2 3
P
课堂小结
2.超几何分布的均值
1.超几何分布
第4课时 二项分布与超几何分布的关系
D
B
C
请做:课时作业(二十一)
2
0
2
2
★衡水重点中学★
《高考调研》
看
观
谢
谢
本节课你有哪些收获?请做一下总结!
课堂反思
7.4.2 超几何分布
温故知新
2.二项分布
X 0 1 k n
P
1.n重伯努利试验
新课讲解
超几何分布
一般地,假设一批产品共有N件,其中有M件次品. 从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
如果随机变量X的分布列具有上式的形式,
那么称随机变量X服从超几何分布.
新课讲解
超几何分布
1.公式中个字母的含义
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
2.求分布列时可以直接利用组合数的意义列式计算,不必机械记忆这个概率分布列.
3. “任取n件,恰有z件次品”是一次性抽取,用组合数列式.
4.各对应的概率和必须为1.
典型例题
解:
例4.从50名学生中随机选出5名学生代表,求甲被选中的概率.
设X表示选出的5名数学中含甲的人数(只能取0或1),
则X服从超几何分布,
且N=50,M=1,n=5,
因此甲被选中的概率为
方法归纳
1.判断随机变量是否服从超几何分布;
2.根据已知条件,确定M,N,n对应的值;
3.代入超几何分布的概率公式,求出结果;
超几何分布的使用步骤:
典型例题
解:
另解:
例5. 一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检
测,求至少有1件不合格的概率.
巩固训练
1.学校要从12名候选人中选4名同学组成学生会,已知有4名候选人来自甲班.假设每名候选人都有相同的机会被选到,
(1)求甲班恰有2名同学被选到的概率.
(2)求甲班至多1名同学被选到的概率
解:
(1)设甲班恰有X人被选到,
则X服从超几何分布,
且N=12,M=4,n=4,
(2)
巩固训练
解:
2. 一袋中有7个大小相同的小球,其中有2个红球,3个黄球,2个蓝球,从中任取3个球.
(1)求红、黄、蓝三种颜色的小球各取1个的概率.
(2)设X表示取到的蓝色小球的个数,求X的分布列和数学期望.
X 0 1 2
P
课堂探究
探究: 服从超几何分布的随机变量的均值是什么
新课讲解
超几何分布的均值
若X服从超几何分布,
典型例题
解:
例6.一袋中有100个大小相同的小球,其中有40个黄球,60个白球,从中随机摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回和不放回摸球,求X的分布列;
(2)分别就有放回和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
新课讲解
解(2)
采用不放回摸球估算的结果更可靠些
新课讲解
0.05
0
0.10
0.15
0.20
0.25
两种摸球方式下,随机变量X服从二项分布和超几何分布.
这两种分布的均值相等都等于8.
但从两种分步的概率分步图看,超几何分布更集中在均值附近.
当n远远小于N时,每次抽取一次,对N的影响很小.
此时,超几何分布可以用二项分步近似.
辨析
二项分布与超几何分布区别和联系
1.区别
一般地,超几何分布的模型是“取次品”是不放回抽样,
而二项分布的模型是“独立重复试验”对于抽样,则是有放回抽样.
2.联系
当次品的数量充分大,且抽取的数量较小时,即便是不放回抽样,也可视其为二项分布.
巩固训练
1. PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的可入肺颗粒物,根据现行国家标 准GB3095-2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2018年全年每天的PM2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
PM2.5日均值(微克/立方米) [25,35) [35,45) [45,55) [55,65) [65,75) [75,85]
频数 3 1 1 1 1 3
(1)从这10天的PM2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ 的分布列.
新课讲解
X 0 1 2 3
P
课堂小结
2.超几何分布的均值
1.超几何分布
第4课时 二项分布与超几何分布的关系
D
B
C
请做:课时作业(二十一)
2
0
2
2
★衡水重点中学★
《高考调研》
看
观
谢
谢
本节课你有哪些收获?请做一下总结!
课堂反思
同课章节目录
