第六章反比例函数专项复习卷(含解析)2023--2024学年北师大版数学九年级上册
文档属性
| 名称 | 第六章反比例函数专项复习卷(含解析)2023--2024学年北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 11:30:37 | ||
图片预览



文档简介
第六章 反比例函数专项复习卷
一.反比例函数的定义(共4小题)
1.(2023 天山区校级开学)下列各式中、均不为,和成反比例的是
A. B. C. D.
2.(2022秋 九龙坡区期末)下列函数中,是的反比例函数的是
A. B. C. D.
3.(2023春 灌云县月考)已知与成反比例,且其函数图象经过点.
(1)求与的函数关系式;
(2)求当时,的值.
4.(2022秋 沂南县期末)下列函数关系式中属于反比例函数的是
A. B. C. D.
二.反比例函数的图象(共1小题)
5.(2023 平阴县一模)反比例函数与一次函数在同一坐标系中的大致图象可能是
A. B.
C. D.
三.反比例函数的性质(共3小题)
6.(2022秋 海淀区校级期末)双曲线截直线,所得的线段长度为 .
7.(2023秋 安乡县月考)若的取值范围如图所示,则在反比例函数的图象的每一个分支上,随的增大而 .
8.(2023春 灌云县期末)若反比例函数的图象在第一、三象限,则的取值范围是 .
四.反比例函数系数k的几何意义(共7小题)
9.(2023 河东区一模)如图,在平面直角坐标系中,点在第一象限,轴于点,函数的图象与线段交于点,且.若的面积为12,则的值为
A.4 B.6 C.8 D.12
10.(2023春 卧龙区期中)如图,若反比例函数的图象经过点,轴于点,且的面积3,则的值为
A. B. C.3 D.6
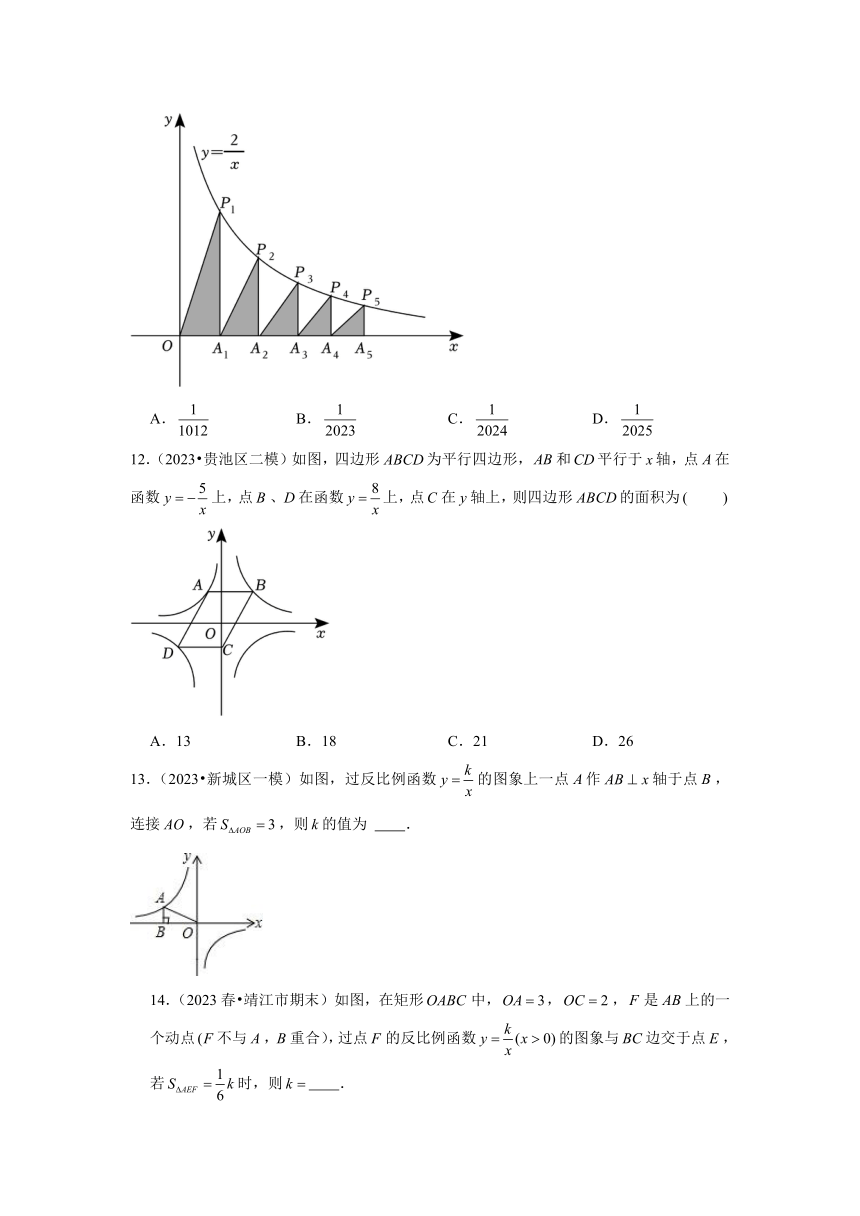
11.(2023 鼓楼区校级三模)如图,在轴的正半轴上依次截取,过点,,,分别作轴的垂线与反比例函数的图象相交于点,,,得△,△,△,并设其面积分别为,,,以此类推,则的值为
A. B. C. D.
12.(2023 贵池区二模)如图,四边形为平行四边形,和平行于轴,点在函数上,点、在函数上,点在轴上,则四边形的面积为
A.13 B.18 C.21 D.26
13.(2023 新城区一模)如图,过反比例函数的图象上一点作轴于点,连接,若,则的值为 .
14.(2023春 靖江市期末)如图,在矩形中,,,是上的一个动点不与,重合),过点的反比例函数的图象与边交于点,若时,则 .
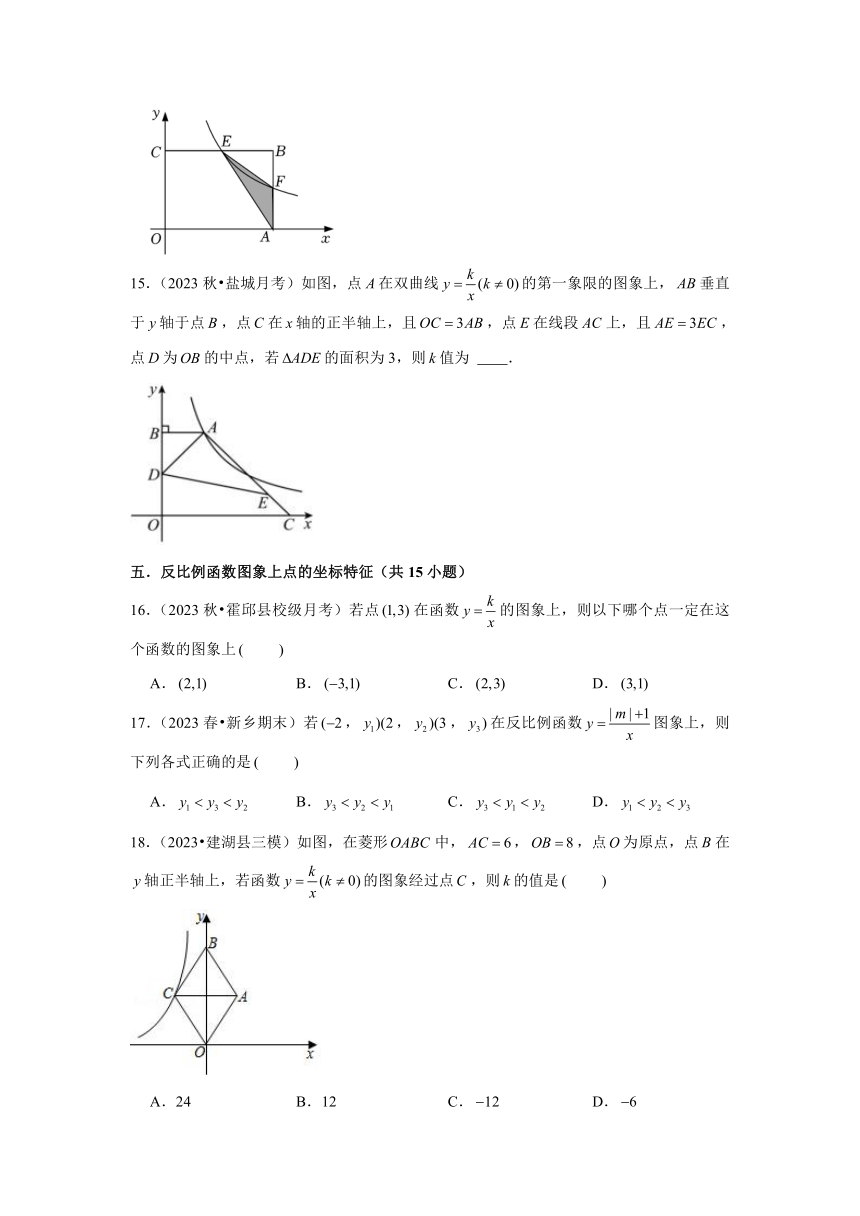
15.(2023秋 盐城月考)如图,点在双曲线的第一象限的图象上,垂直于轴于点,点在轴的正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则值为 .
五.反比例函数图象上点的坐标特征(共15小题)
16.(2023秋 霍邱县校级月考)若点在函数的图象上,则以下哪个点一定在这个函数的图象上
A. B. C. D.
17.(2023春 新乡期末)若,,,在反比例函数图象上,则下列各式正确的是
A. B. C. D.
18.(2023 建湖县三模)如图,在菱形中,,,点为原点,点在轴正半轴上,若函数的图象经过点,则的值是
A.24 B.12 C. D.
19.(2023春 辉县市期末)若点,,在反比例函数图象上,则下列结论正确的是
A. B. C. D.
20.(2023 楚雄市校级二模)如图,矩形在平面直角坐标系中,点,轴,且,,若反比例函数与矩形有交点,则的取值范围是
A. B. C. D.
21.(2022秋 武安市期末)已知反比例函数的图象在各自象限内,随的增大而增大,则下列各点可能在这个函数图象上的是
A. B. C. D.
22.(2023春 市中区期末)若点、、在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
23.(2023 遂溪县一模)若点,,,,,都在反比例函数的图象上,则,,的大小关系是
A. B. C. D.
24.(2023秋 庐阳区校级期中)已知点在反比例函数图象上,则点一定在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
25.(2023 襄阳)点,都在反比例函数的图象上,则 .(填“”或“”
26.(2023秋 蒙城县月考)如图,已知反比例函数,在第一象限的图象,过上任意一点,作轴的平行线交于点,交轴于点过点作轴的垂线交于点,交轴于点,连接,,则:
①的面积为 ;
② .
27.(2023秋 如皋市期中)在平面直角坐标系中,若点和点都在反比例函数的图象上,则 (填“”“ ”或“” .
28.(2023 香坊区校级开学)在反比例函数的图象上有两点,和,,若时,则 (填“”、“ ”、“ ” .
29.(2022秋 天心区期末)若点,,在反比例函数的图象上,则,,的大小关系是 .
30.(2023 巴东县模拟)如图,在平面直角坐标系中,为坐标原点,双曲线经过的顶点与斜边中点.
(1)求;
(2)若双曲线经过点,求.
六.待定系数法求反比例函数解析式(共1小题)
31.(2022秋 徐汇区期末)已知,与成正比例,与成反比例,且当时,;当时,.
(1)求关于的函数解析式;
(2)当时,求的值.
七.反比例函数与一次函数的交点问题(共13小题)
32.(2023 咸丰县一模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,连接,.
(1)求反比例函数的表达式;
(2)求的面积.
33.(2022秋 玉泉区校级期末)如图,一次函数的图象分别交轴、轴于,两点,交反比例函数图象于,两点.
(1)求直线的表达式;
(2)点是线段上一点,若,求点的坐标;
(3)请你根据图象直接写出不等式的解集.
34.(2023春 罗定市校级期中)如图所示,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集.
35.(2023秋 来宾期中)如图,直线与反比例函数的图象相交于点、,与轴交于点,其中点的坐标为,点的横坐标为.
(1)试确定反比例函数的表达式;
(2)求的坐标.
36.(2023春 长春期中)如图,正比例函数的图象与反比例函数的图象相交于、两点,点的横坐标为2,当时,的取值范围是
A.或 B.或
C.或 D.或
37.(2023春 安溪县期中)若直线与双曲线交于点,,,,则的值为
A.2023 B. C. D.
38.(2023秋 温江区校级期中)如图,直线交轴于点,交反比例函数于点,以为边的正方形的顶点在轴上,顶点在双曲线上,则的值为 .
39.(2023秋 泰山区期中)如图,直线与双曲线交于、两点,过点作轴,垂足为点,连接,若,则的值是 .
40.(2023 大东区模拟)如图,直线交轴于点,交反比例函数的图象于,两点,过点作轴,垂足为点,连接,若,则的值为 .
41.(2023秋 朝阳区校级期中)在平面直角坐标系中,记函数的图象为,直线经过,与图象交于,两点.
(1)求的值;
(2)横、纵坐标都是整数的点叫做整点.记图象在,之间的部分与线段围成的区域(不含边界)为.
①当时,区域内的整点个数为 个;
②各区域内恰有4个整点,结合函数图象,的取值范围为 .
42.(2023秋 兴宾区期中)如图,一次函数的图象与反比例函数的图象交于第一象限,两点,与坐标轴交于、两点,连接,是坐标原点).
(1)求反比例函数的表达式;
(2)求的面积;
43.(2023 泰山区校级自主招生)在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,过点作轴,垂足为,,,点的坐标为.
(1)求的周长和面积;
(2)求该反比例函数和一次函数的解析式.
44.(2023 肇源县开学)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
八.根据实际问题列反比例函数关系式(共1小题)
45.(2022秋 丛台区校级期末)验光师测的一组关于近视眼镜的度数与镜片的焦距的数据,如表:
(单位:度) 100 200 400 500
(单位:米) 1.00 0.50 0.25 0.20
则关于的函数关系式是 .
九.反比例函数的应用(共4小题)
46.(2023 淮阳区三模)如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示.
2 1 0.5 0.4
桌面所受压强 100 200 400 500 800
(1)根据表中数据,求桌面所受压强与受力面积之间的函数表达式及的值.
(2)现想将另一长、宽、高分别为,,,且与该长方体相同重量的长方体按如图2所示的方式(即面向上)放置于该水平玻璃桌面上.若该玻璃桌面能承受的最大压强为,请你判断这种摆放方式是否安全?并说明理由.若将此长方体面向下摆放,请直接判断是否安全.
47.(2022秋 南华县期末)元旦假期,李老师驾驶小汽车从甲地匀速行驶到乙地,当小汽车匀速行驶的速度为时,行驶时间为;设小汽车匀速行驶的速度为,行驶的时间为.
(1)求关于的函数表达式;
(2)若小汽车匀速行驶的速度为,则从乙地返回甲地需要几小时?
48.(2023秋 房山区期中)已知蓄电池两端电压为定值,电流与的函数关系为,当时,,则当时,的值为
A. B. C. D.
49.(2023 东阳市三模)
设计货船通过双曲线桥的方案
素材1 一座曲线桥如图1所示,当水面宽米时,桥洞顶部离水面距离米.已知桥洞形如双曲线,图2是其示意图,且该桥关于对称.
素材2 如图4,一艘货船露出水面部分的横截面为矩形,测得米,米.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度(米与货船增加的载重量(吨满足函数表达式.
问题解决
任务1 确定桥洞的形状 ①建立平面直角坐标系如图3所示,显然,落在第一象限的角平分线上. 甲说:点可以在第一象限角平分线的任意位置. 乙说:不对吧?当点落在,时,点的坐标为 ,此时过点的双曲线的函数表达式为 ,而点所在双曲线的函数表达式为显然不符合题意.
任务2 拟定方案 此时货船能通过该桥洞吗?若能,请说明理由;若不能,至少要增加多少吨货物?
一十.反比例函数综合题(共2小题)
50.(2023秋 金水区校级期中)如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内,两点在右侧),分别交轴,轴于,两点.
(1)求和的值;
(2)求点的坐标;
(3)在轴上是否存在一点,使以,,为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
51.(2023 青岛模拟)如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于、两点,过点作轴于点,,,点的坐标为
(1)求一次函数和反比例函数的表达式;
(2)是轴上一点,且是等腰三角形,请直接写出所有符合条件的点坐标.
第六章 反比例函数专项复习卷
参考答案与试题解析
一.反比例函数的定义(共4小题)
1.(2023 天山区校级开学)下列各式中、均不为,和成反比例的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义:为常数且,逐一判断即可解答.
【解答】解:、,
,
和成正比例,
故不符合题意;
、,
,
和成正比例,
故不符合题意;
、,
,
和成反比例,
故符合题意;
、,
,
和不成比例,
故不符合题意;
故选:.
2.(2022秋 九龙坡区期末)下列函数中,是的反比例函数的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义回答即可.
【解答】解:、该函数是正比例函数,故本选项不符合题意;
、该函数不是反比例函数,故本选项不符合题意;
、该函数是正比例函数,故本选项不符合题意;
、该函数是反比例函数,故本选项符合题意.
故选:.
3.(2023春 灌云县月考)已知与成反比例,且其函数图象经过点.
(1)求与的函数关系式;
(2)求当时,的值.
【答案】(1);
(2).
【分析】(1)由于与成反比例,设,代入,解得的值即可;
(2)将代入反比例函数解析式,解得的值即可.
【解答】解:(1)设与的函数关系式为,
又图象经过点,则,
与的函数关系式为.
故答案为:;
(2)将代入,得到,
当时,.
4.(2022秋 沂南县期末)下列函数关系式中属于反比例函数的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义逐项判断选项求解.
【解答】解:为正比例函数,选项不符合题意.
为一次函数,选项不符合题意.
为二次函数,选项不符合题意.
为反比例函数,选项符合题意.
故选:.
二.反比例函数的图象(共1小题)
5.(2023 平阴县一模)反比例函数与一次函数在同一坐标系中的大致图象可能是
A. B.
C. D.
【答案】
【分析】根据一次函数图象判定、的符号,根据的符号判定反比例函数图象所在的象限.
【解答】解:、一次函数的图象经过第一、三象限,则,与轴交于负半轴,则,所以,则反比例经过第二、四象限,不符合题意;
、一次函数的图象经过第二、四象限,则,与轴交于负半轴,则,所以,则反比例经过第一、三象限,不符合题意;
、一次函数的图象经过第二、四象限,则,与轴交于正半轴,则,所以,则反比例经过第二、四象限,不符合题意;
、一次函数的图象经过第一、三象限,则,与轴交于负半轴,则,所以,则反比例经过第二、四象限,符合题意;
故选:.
三.反比例函数的性质(共3小题)
6.(2022秋 海淀区校级期末)双曲线截直线,所得的线段长度为 .
【答案】.
【分析】解析式联立成方程组,解方程组求得交点坐标,进一步即可求得所截线段的长度.
【解答】解:由解得或,
双曲线与直线的交点为,,
所截得的线段的长度为:,
故答案为:.
7.(2023秋 安乡县月考)若的取值范围如图所示,则在反比例函数的图象的每一个分支上,随的增大而 增大 .
【答案】增大.
【分析】由图得,即,得,故反比例函数的图象在二四象限,故反比例函数的图象的每一个分支上,随的增大而增大.
【解答】解:由图得,即,
得,
故反比例函数的图象在二四象限,
故反比例函数的图象的每一个分支上,随的增大而增大.
故答案为:增大.
8.(2023春 灌云县期末)若反比例函数的图象在第一、三象限,则的取值范围是 .
【答案】.
【分析】根据反比例函数的图象在第一、第三象限列出关于的不等式,求出的取值范围即可.
【解答】解:反比例函数的图象在第一、第三象限,
,解得.
故答案为:.
四.反比例函数系数k的几何意义(共7小题)
9.(2023 河东区一模)如图,在平面直角坐标系中,点在第一象限,轴于点,函数的图象与线段交于点,且.若的面积为12,则的值为
A.4 B.6 C.8 D.12
【答案】
【分析】连接,如图,根据三角形面积公式,由得到,可计算出,再根据反比例函数比例系数的几何意义得到,然后去绝对值即可得到满足条件的的值.
【解答】解:连接,如图,
轴于点,,
,
,
,
而,
.
故选:.
10.(2023春 卧龙区期中)如图,若反比例函数的图象经过点,轴于点,且的面积3,则的值为
A. B. C.3 D.6
【答案】
【分析】根据反比例函数比例系数的几何意义即可解决问题.
【解答】解:连接,,
轴于点,
.
.
.
反比例函数的图象在第一、三象限,
.
.
故选:.
11.(2023 鼓楼区校级三模)如图,在轴的正半轴上依次截取,过点,,,分别作轴的垂线与反比例函数的图象相交于点,,,得△,△,△,并设其面积分别为,,,以此类推,则的值为
A. B. C. D.
【答案】
【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是个定值,,由反比例函数解析式中,得出△,△,△,,△的面积都为1,而为的,且△与△的高为同一条高,故△的面积为△的面积的,由△的面积都为1,得出△的面积,即为的值.
【解答】解:连接,,,,如图所示:
过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是个定值,,
,即,
又,
,
,,,,,
△与△的高为同一条高,
,
.
故选:.
12.(2023 贵池区二模)如图,四边形为平行四边形,和平行于轴,点在函数上,点、在函数上,点在轴上,则四边形的面积为
A.13 B.18 C.21 D.26
【答案】
【分析】作轴于,轴于,轴于,根据平行四边形的面积公式以及反比例函数系数的几何意义即可求得.
【解答】解:作轴于,轴于,轴于,
四边形为平行四边形,和平行于轴,
,,
.
故选:.
13.(2023 新城区一模)如图,过反比例函数的图象上一点作轴于点,连接,若,则的值为 .
【分析】先设出点的坐标,由的面积可求出的值,即,即可写出反比例函数的解析式.
【解答】解:设点坐标为,
由图可知点在第二象限,
,,
又轴,
,,
,
,
故答案为:.
14.(2023春 靖江市期末)如图,在矩形中,,,是上的一个动点不与,重合),过点的反比例函数的图象与边交于点,若时,则 4 .
【答案】4.
【分析】连接,利用同底面积比等于高之比,得到点坐标,再利用反比例函数的关系式的求法计算即可.
【解答】解:连接,
由题意得:三角形的面积,
,
,
,,
,
,
故答案为:4.
15.(2023秋 盐城月考)如图,点在双曲线的第一象限的图象上,垂直于轴于点,点在轴的正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则值为 4 .
【答案】4.
【分析】由,的面积为3,得到的面积为1,则的面积为4,设点坐标为,则,,,,利用得,整理可得,即可得到的值.
【解答】解:连,如图,
,的面积为3,
的面积为1,
的面积为4,
设点坐标为,则,,
而点为的中点,
,
,
,
,
把代入双曲线,
.
故答案为:4.
五.反比例函数图象上点的坐标特征(共15小题)
16.(2023秋 霍邱县校级月考)若点在函数的图象上,则以下哪个点一定在这个函数的图象上
A. B. C. D.
【答案】
【分析】先求出的值,再根据双曲线上的点的横纵坐标之积等于,进行判断即可.
【解答】解:点在函数的图象上,
,
,,,,
点一定在这个函数的图象上.
故选:.
17.(2023春 新乡期末)若,,,在反比例函数图象上,则下列各式正确的是
A. B. C. D.
【答案】
【分析】根据反比例函数的性质得出函数图象在第一、三象限,并且在每个象限内,随的增大而减小,再根据反比例函数的性质比较即可.
【解答】解:反比例函数数中,
函数图象在第一、三象限,并且在每个象限内,随的增大而减小,
点,,,在反比例函数图象上,,
,,
即,
故选:.
18.(2023 建湖县三模)如图,在菱形中,,,点为原点,点在轴正半轴上,若函数的图象经过点,则的值是
A.24 B.12 C. D.
【答案】
【分析】先根据菱形的性质求出点坐标,再把点坐标代入反比例函数的解析式即可得出的值.
【解答】解:在菱形中,,,
,
反比例函数的图象经过点,
.
故选:.
19.(2023春 辉县市期末)若点,,在反比例函数图象上,则下列结论正确的是
A. B. C. D.
【答案】
【分析】由题意可知函数的图象在一、三象限,由三点的横坐标可知点,在第三象限,在第一象限,根据反比例函数的增减性及各象限内点的坐标特点即可解答.
【解答】解:反比例函数中,,
此函数的图象在一、三象限,在每一象限内,随的增大而减小;
,,
点,在第三象限,在第一象限,
,,
,
故选:.
20.(2023 楚雄市校级二模)如图,矩形在平面直角坐标系中,点,轴,且,,若反比例函数与矩形有交点,则的取值范围是
A. B. C. D.
【答案】
【分析】根据矩形的性质求得点的坐标,把、的坐标分别代入求得的值,根据图象即可求解.
【解答】解:矩形的边,,点,
,
当反比例函数经过点时,则;
当反比例函数经过点时,则,
若反比例函数与矩形有交点,则的取值范围是:,
故选:.
21.(2022秋 武安市期末)已知反比例函数的图象在各自象限内,随的增大而增大,则下列各点可能在这个函数图象上的是
A. B. C. D.
【答案】
【分析】根据反比例函数的性质判断即可.
【解答】解:因为反比例函数的图象在各自象限内,随的增大而增大,
所以,
.,故本选项符合题意;
.,故本选项不符合题意;
.,故本选项不符合题意;
.,故本选项不符合题意;
故选:.
22.(2023春 市中区期末)若点、、在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
【答案】
【分析】根据反比例函数图象上点的坐标特征求出、、的值,比较后即可得出结论.
【解答】解:点,,在反比例函数的图象上,
,,,
又,
.
故选:.
23.(2023 遂溪县一模)若点,,,,,都在反比例函数的图象上,则,,的大小关系是
A. B. C. D.
【答案】
【分析】直接把各点坐标代入反比例函数的解析式,求出,,的值,再比较大小即可.
【解答】解:点,,,,,都在反比例函数的图象上,
,解得;
,解得;
,解得,
,
.
故选:.
24.(2023秋 庐阳区校级期中)已知点在反比例函数图象上,则点一定在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【分析】把点代入反比例函数解析式,可得,可得点一定在第一象限.
【解答】解:点在反比例函数图象上,
,
,
点一定在第一象限.
故选:.
方法二:
反比例函数中,,
图象的两个分支在一、三象限,
点在反比例函数的图象上,
点一定在第一象限.
故选:.
25.(2023 襄阳)点,都在反比例函数的图象上,则 .(填“”或“”
【答案】.
【分析】根据反比例函数的第一象限图象上,随的增大而减小判断即可.
【解答】解:点,在反比例函数的第一象限图象上,随的增大而减小,
.
故答案为:.
26.(2023秋 蒙城县月考)如图,已知反比例函数,在第一象限的图象,过上任意一点,作轴的平行线交于点,交轴于点过点作轴的垂线交于点,交轴于点,连接,,则:
①的面积为 ;
② .
【答案】,.
【分析】设点的坐标为,则,,,,,由此即可得出,结合即可证出,再根据相似三角形的性质即可得出的值,再利用相似三角形的性质求出的面积.
【解答】解:设点的坐标为,
作轴的平行线交于,交轴于点,过点作轴的垂线交于,交轴于点,
,,,,,
,,,,
.
又,
,
.
,
,
.
故答案为:,.
27.(2023秋 如皋市期中)在平面直角坐标系中,若点和点都在反比例函数的图象上,则 (填“”“ ”或“” .
【答案】
【分析】根据函数的增减性先看两个点是否在同一个象限内,比较两个点横坐标的大小即可确定值的大小.
【解答】解:在反比例函数中,,
在每一象限内,随的增大而减小,
点,都在第一象限,,
.
故答案为:.
28.(2023 香坊区校级开学)在反比例函数的图象上有两点,和,,若时,则 (填“”、“ ”、“ ” .
【答案】.
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断出和的大小关系.
【解答】解:反比例函数,
该函数的图象位于第一、三象限,在每个象限内,随的增大而减小,第一象限内的都大于0,第三象限内的都小于0,
,
,
故答案为:.
29.(2022秋 天心区期末)若点,,在反比例函数的图象上,则,,的大小关系是 .
【答案】.
【分析】先由得到函数在第二象限和第四象限内的函数值随的增大而增大,然后得到,,的大小关系.
【解答】解:反比例系数,
函数在第二象限和第四象限内的函数值随的增大而增大,
,
,
故答案为:.
30.(2023 巴东县模拟)如图,在平面直角坐标系中,为坐标原点,双曲线经过的顶点与斜边中点.
(1)求;
(2)若双曲线经过点,求.
【答案】或.
【分析】(1)将点代入,即可得出的值;
(2)过点,,分别作轴的垂线,垂足分别为,,,先由点得,,证和相似得,据此可设,,则点的坐标为,再由中点坐标公式得点,然后将点代入列出关于的方程,解方程求出的值,继而得点的坐标,进而可求出的值.
【解答】解:(1)双曲线经过点,
.
(2)过点,分别作轴的垂线,垂足分别为,,
点,
,,
,
,
又,
,
,
,
,
可设,,
点的坐标为,
点为的中点,点,
由中点坐标公式得点的坐标为,
双曲线经过点,
,
解得:,,
点或,
双曲线经过点,
或.
六.待定系数法求反比例函数解析式(共1小题)
31.(2022秋 徐汇区期末)已知,与成正比例,与成反比例,且当时,;当时,.
(1)求关于的函数解析式;
(2)当时,求的值.
【答案】(1).
(2).
【分析】(1)根据正比例函数和反比例函数的定义设,,则,再把两组对应值代入得到关于、的方程组,然后解方程组求出、即可.
(2)把代入(1)中求得的解析式即可求得.
【解答】解:(1)设,,
则,
根据题意得,
解得.
所以与的函数表达式为.
(2)把代入得,.
七.反比例函数与一次函数的交点问题(共13小题)
32.(2023 咸丰县一模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,连接,.
(1)求反比例函数的表达式;
(2)求的面积.
【答案】(1);(2)60.
【分析】(1)把代入,从而可得答案;
(2)先求解两个函数的交点坐标,再求解一次函数与轴的交点坐标,再利用三角形的面积之差可得答案.
【解答】解:(1)把代入,
,
;
(2)由题意可得:,
,
整理得:,
解得:,,
方程组的解为:或,经检验符合题意;
,
如图,记与坐标轴的交点为,,
由可得:当可得,
,
.
33.(2022秋 玉泉区校级期末)如图,一次函数的图象分别交轴、轴于,两点,交反比例函数图象于,两点.
(1)求直线的表达式;
(2)点是线段上一点,若,求点的坐标;
(3)请你根据图象直接写出不等式的解集.
【答案】(1);(2);(3)②或.
【分析】(1)把点代入中,利用待定系数法求得反比例函数的解析式,进而求得的坐标,然后根据待定系数法即可求得直线的表达式;
(2)设点的坐标为,求得点的坐标为,得到,根据得出关的方程,解方程求得,从而求得点的坐标;
(3)根据图象即可求得.
【解答】(1)把点代入中,得:,
反比例函数的解析式为,
将点代入得,
设直线的表达式为,则有,
解得,
直线的表达式为;
(2)设点的坐标为,
点的坐标为,,
,
,
解得:,
点的坐标为;
(3)不等式的解集是,.
34.(2023春 罗定市校级期中)如图所示,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集.
【答案】(1)反比例函数的表达式,一次函数的表达式;
(2)不等式的解集是或.
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)一次函数的值小于反比例函数的值的的取值范围,就是对应的一次函数的图象在反比例函数的图象的下边的自变量的取值范围.
【解答】解:(1)将点坐标代入反比例函数解析式中,得,
,
反比例函数的表达式,
将点代入得,
,
将、点代入中,得,
解得,
一次函数的表达式;
(2)不等式的解集是或.
35.(2023秋 来宾期中)如图,直线与反比例函数的图象相交于点、,与轴交于点,其中点的坐标为,点的横坐标为.
(1)试确定反比例函数的表达式;
(2)求的坐标.
【答案】(1)反比例函数的关系式为:;
(2).
【分析】(1)把点的坐标代入反比例函数中,可得的值,即可得出反比例函数的关系式;
(2)先利用待定系数法求一次函数的解析式,再令,可得点的坐标.
【解答】解:(1)点在反比例函数的图象上,
,
反比例函数的关系式为:;
(2)当时,,
,
把点和代入得:,
解得:,
,
当时,,
,
.
36.(2023春 长春期中)如图,正比例函数的图象与反比例函数的图象相交于、两点,点的横坐标为2,当时,的取值范围是
A.或 B.或
C.或 D.或
【答案】
【分析】由正、反比例的对称性结合点的横坐标即可得出点的横坐标,根据函数图象的上下位置关系结合交点的横坐标,即可得出不等式的解集.
【解答】解:正比例函数与反比例函数的图象均关于原点对称,点的横坐标为2,
点的横坐标为.
观察函数图象,发现:
当或时,正比例函数图象在反比例函数图象的上方,
当时,的取值范围是或.
故选:.
37.(2023春 安溪县期中)若直线与双曲线交于点,,,,则的值为
A.2023 B. C. D.
【答案】
【分析】根据反比例函数图象上点的坐标特征,两交点坐标关于原点对称,得到,,再代入得出答案.
【解答】解:由反比例函数图象上点的坐标特征可知点,,,关于原点对称,
,,
把,代入双曲线,得,
,
故选:.
38.(2023秋 温江区校级期中)如图,直线交轴于点,交反比例函数于点,以为边的正方形的顶点在轴上,顶点在双曲线上,则的值为 .
【答案】.
【分析】作轴于,轴于,先求得、的坐标,然后通过证得,得到,,即可求得,代入即可求得的值.
【解答】解:作轴于,轴于,
反比例函数过点,
,
,
,
,,
令,则,
,
,
,
四边形是正方形,
,,
,
,
,
,
,
,,
,
,
顶点在双曲线上,
,
故答案为:.
39.(2023秋 泰山区期中)如图,直线与双曲线交于、两点,过点作轴,垂足为点,连接,若,则的值是 .
【答案】.
【分析】先求出的面积,再根据反比例函数中的几何意义即可解决问题.
【解答】解:因为直线与双曲线交于、两点,
所以,两点关于坐标原点成中心对称,
即,
所以.
又因为,
所以.
所以,
解得.
又反比例函数图象位于第二、四象限,
所以,
所以.
故答案为:.
40.(2023 大东区模拟)如图,直线交轴于点,交反比例函数的图象于,两点,过点作轴,垂足为点,连接,若,则的值为 10 .
【答案】10.
【分析】根据反比例函数系数的几何意义即可求解.
【解答】解:连接,
轴,
,
轴,
,
,
,
,
解得:,
故答案为:10.
41.(2023秋 朝阳区校级期中)在平面直角坐标系中,记函数的图象为,直线经过,与图象交于,两点.
(1)求的值;
(2)横、纵坐标都是整数的点叫做整点.记图象在,之间的部分与线段围成的区域(不含边界)为.
①当时,区域内的整点个数为 6 个;
②各区域内恰有4个整点,结合函数图象,的取值范围为 .
【答案】(1)4;(2)①6;②.
【分析】(1)将点的坐标代入一次函数关系式可得答案;
(2)①结合图象分析可得答案;
②考虑临界位置,结合图象得出答案.
【解答】解:(1)直线经过点,
,
解得,
所以;
(2)①如图所示,区域内的整点有,,,,,,共6个.
故答案为:6;
②当时,区域内有4个整点,如图所示.
当时,区域内有4个整点,如图所示.
所以区域内有4个整点,的取值范围是.
故答案为:.
42.(2023秋 兴宾区期中)如图,一次函数的图象与反比例函数的图象交于第一象限,两点,与坐标轴交于、两点,连接,是坐标原点).
(1)求反比例函数的表达式;
(2)求的面积;
【答案】(1)为;(2)7.5.
【分析】(1)把代入求出,把代入求出即可;
(2)把,代入得出解析式,求出,,得出一次函数的解析式,把代入求出,得出,根据的面积代入求出即可.
【解答】解:(1)把代入,得,
反比例函数的表达式为:;
(2)把,代入得,
解得,,
一次函数的解析式为,
把代入,得,
,
.
43.(2023 泰山区校级自主招生)在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,过点作轴,垂足为,,,点的坐标为.
(1)求的周长和面积;
(2)求该反比例函数和一次函数的解析式.
【分析】(1)根据正切函数,可得的长,根据勾股定理,可得的长,根据三角形的周长和面积,可得答案;
(2)根据待定系数法,可得函数解析式.
【解答】解:(1)由,得
.即.
由勾股定理,得
,
的周长,
的面积;
(2)将点坐标代入得
,
反比例函数的解析式为;
当时,,解得,即.
将、点坐标代入,得,
解得,
一次函数的解析式为.
44.(2023 肇源县开学)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
【答案】(1)反比例函数的解析式为;
(2)不等式的解集为或;
(3)点的坐标为或.
【分析】(1)先通过一次函数求出点坐标,利用待定系数法即可求出反比例函数解析式;
(2)求出点的坐标,根据图象求解即可;
(3)根据图象求出,再根据求出,即可求出.
【解答】解:(1)把点代入直线得:,
点的坐标为:,
反比例函数的图象过点,
,
即反比例函数的解析式为,
(2)由(1)得:点的坐标为:,
同理可求,点的坐标为:,
不等式的解集为或;
(3)把代入得:,
即点的坐标为:,
,
,
,
,
当点的纵坐标为3时,则,解得,
当点的纵坐标为时,则,解得,
点的坐标为或.
八.根据实际问题列反比例函数关系式(共1小题)
45.(2022秋 丛台区校级期末)验光师测的一组关于近视眼镜的度数与镜片的焦距的数据,如表:
(单位:度) 100 200 400 500
(单位:米) 1.00 0.50 0.25 0.20
则关于的函数关系式是 .
【分析】根据表格数据可得近视眼镜的度数与镜片的焦距成反比例,设关于的函数关系式是,再代入一对、的值可得的值,进而可得答案.
【解答】解:根据表格数据可得近视眼镜的度数与镜片的焦距成反比例,
设关于的函数关系式是,
,,
,
解得:,
关于的函数关系式是.
故答案为:.
九.反比例函数的应用(共4小题)
46.(2023 淮阳区三模)如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示.
2 1 0.5 0.4
桌面所受压强 100 200 400 500 800
(1)根据表中数据,求桌面所受压强与受力面积之间的函数表达式及的值.
(2)现想将另一长、宽、高分别为,,,且与该长方体相同重量的长方体按如图2所示的方式(即面向上)放置于该水平玻璃桌面上.若该玻璃桌面能承受的最大压强为,请你判断这种摆放方式是否安全?并说明理由.若将此长方体面向下摆放,请直接判断是否安全.
【答案】(1),;
(2)这种摆放方式安全,理由见解析.
【分析】(1)用待定系数法可得函数关系式;
(2)算出,即可求出,比较可得答案.
【解答】解:(1)由表格可知,压强与受力面积的乘积不变,故压强是受力面积的反比例函数,
设,将代入得:
,
解得,
桌面所受压强与受力面积之间的函数表达式为,
把代入得,;
(2)这种摆放方式安全,理由如下:
由图可知,
将长方体放置于该水平玻璃桌面上,,
,
这种摆放方式安全.
47.(2022秋 南华县期末)元旦假期,李老师驾驶小汽车从甲地匀速行驶到乙地,当小汽车匀速行驶的速度为时,行驶时间为;设小汽车匀速行驶的速度为,行驶的时间为.
(1)求关于的函数表达式;
(2)若小汽车匀速行驶的速度为,则从乙地返回甲地需要几小时?
【答案】(1);
(2)小汽车速度为时,从乙地到甲地需要.
【分析】(1)根据路程,速度,时间的关系,先求出从甲地到乙地路程,再列出函数关系式;
(2)结合(1),把代入求出的值即可.
【解答】解:(1)由题意可得从甲地到乙地路程为:,
与的关系式为:;
(2)当小汽车匀速行驶的速度为,即,
在中,令得,
解得,
答:小汽车速度为时,从乙地到甲地需要.
48.(2023秋 房山区期中)已知蓄电池两端电压为定值,电流与的函数关系为,当时,,则当时,的值为
A. B. C. D.
【答案】
【分析】先利用待定系数法求出函数解析式,再将的值代入求值即可.
【解答】解:电流与的函数关系为,当时,,
,
解得,
电流与的函数关系为,
当时,即,
解得.
故选:.
49.(2023 东阳市三模)
设计货船通过双曲线桥的方案
素材1 一座曲线桥如图1所示,当水面宽米时,桥洞顶部离水面距离米.已知桥洞形如双曲线,图2是其示意图,且该桥关于对称.
素材2 如图4,一艘货船露出水面部分的横截面为矩形,测得米,米.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度(米与货船增加的载重量(吨满足函数表达式.
问题解决
任务1 确定桥洞的形状 ①建立平面直角坐标系如图3所示,显然,落在第一象限的角平分线上. 甲说:点可以在第一象限角平分线的任意位置. 乙说:不对吧?当点落在,时,点的坐标为 , ,此时过点的双曲线的函数表达式为 ,而点所在双曲线的函数表达式为显然不符合题意.
任务2 拟定方案 此时货船能通过该桥洞吗?若能,请说明理由;若不能,至少要增加多少吨货物?
【答案】任务,,,乙正确;
任务2:此时货船不能通过该桥洞;要至少增加吨货物此货船能通过该桥洞.
【分析】任务1:设曲线的解析式为,把点,代入,可得曲线的解析式为,再由反比例函数图象的对称性可得:点是的中点,,过点、分别作轴、轴的平行线交于,过点作于,可得、是等腰直角三角形,进而可得,,,,点,在双曲线上与点在双曲线上矛盾;
任务2:设,,其中,则,,可得,由,,可得,,,可得,再根据矩形的性质可得,,即可判断此时货船不能通过;运用待定系数法可得直线的解析式为,进而可得直线与双曲线的交点,,即可求得答案.
【解答】解:任务1:设曲线的解析式为,把点,代入,得:,
解得:,
曲线的解析式为,
落在第一象限的角平分线上,
、关于对称,即、关于第一象限角平分线对称,
点是的中点,,
过点、分别作轴、轴的平行线交于,过点作于,如图,
则、是等腰直角三角形,
,
,
,,
,
,,
,,
,
点,在双曲线上,
点所在双曲线的函数表达式为显然不符合题意.
故答案为:,,,乙正确;
任务2:设,,其中,则,,如图,
点在直线上,
,即,
,,
,,,
,
,
,
,,,,,,,,
四边形是矩形,
,,
,,
,,,,
,
此时货船不能通过该桥洞;
设直线的解析式为,把,代入,得,
解得:,
直线的解析式为,
联立得,
解得:(舍去),,
,,
,即,
,
,
故要至少增加吨货物此货船能通过该桥洞.
答:此时货船不能通过该桥洞;要至少增加吨货物此货船能通过该桥洞.
一十.反比例函数综合题(共2小题)
50.(2023秋 金水区校级期中)如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内,两点在右侧),分别交轴,轴于,两点.
(1)求和的值;
(2)求点的坐标;
(3)在轴上是否存在一点,使以,,为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
【答案】(1),;
(2);
(3)或.
【分析】(1)将点的坐标分别代入一次函数与反比例函数的解析式,解方程即可得出结论;
(2)由(1)知一次函数的解析式为,反比例函数的解析式为,联立可得点;
(3)由一次函数与轴,轴交于,两点,可得,;所以,;设,,,根据图形可知,需要分两种情况,①当时,,②当时,,分别求解可得出结论.
【解答】解:(1)一次函数与反比例函数交于点,
,,
,;
(2)由(1)知一次函数的解析式为,反比例函数的解析式为,
解得,,
;
(3)存在以,,为顶点的三角形与相似.
一次函数与轴,轴交于,两点,
,,
,,
设,
,,
①当时,,
,
,,
;
②当时,,
,
,,,
,
解得,
,
综上所述,或.
51.(2023 青岛模拟)如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于、两点,过点作轴于点,,,点的坐标为
(1)求一次函数和反比例函数的表达式;
(2)是轴上一点,且是等腰三角形,请直接写出所有符合条件的点坐标.
【分析】(1)先根据勾股定理求出,,得出点,进而求出反比例函数解析式,再求出点坐标,最后用待定系数法求出直线解析式;
(2)设出点坐标,进而表示出,,,利用等腰三角形的两边相等建立方程求解即可得出结论.
【解答】解:(1)轴,
,
在中,,,
,,
,
,
又点在反比例函数上,
,
,
点,在直线上,
,
,
直线的表达式为;
(2)设点,
,,
,,,
是等腰三角形,
①当时,
,
,
或,
②当时,
,
(舍或,
,
③时,
,
,
,
即:当点坐标为,,或时,是等腰三角形.
一.反比例函数的定义(共4小题)
1.(2023 天山区校级开学)下列各式中、均不为,和成反比例的是
A. B. C. D.
2.(2022秋 九龙坡区期末)下列函数中,是的反比例函数的是
A. B. C. D.
3.(2023春 灌云县月考)已知与成反比例,且其函数图象经过点.
(1)求与的函数关系式;
(2)求当时,的值.
4.(2022秋 沂南县期末)下列函数关系式中属于反比例函数的是
A. B. C. D.
二.反比例函数的图象(共1小题)
5.(2023 平阴县一模)反比例函数与一次函数在同一坐标系中的大致图象可能是
A. B.
C. D.
三.反比例函数的性质(共3小题)
6.(2022秋 海淀区校级期末)双曲线截直线,所得的线段长度为 .
7.(2023秋 安乡县月考)若的取值范围如图所示,则在反比例函数的图象的每一个分支上,随的增大而 .
8.(2023春 灌云县期末)若反比例函数的图象在第一、三象限,则的取值范围是 .
四.反比例函数系数k的几何意义(共7小题)
9.(2023 河东区一模)如图,在平面直角坐标系中,点在第一象限,轴于点,函数的图象与线段交于点,且.若的面积为12,则的值为
A.4 B.6 C.8 D.12
10.(2023春 卧龙区期中)如图,若反比例函数的图象经过点,轴于点,且的面积3,则的值为
A. B. C.3 D.6
11.(2023 鼓楼区校级三模)如图,在轴的正半轴上依次截取,过点,,,分别作轴的垂线与反比例函数的图象相交于点,,,得△,△,△,并设其面积分别为,,,以此类推,则的值为
A. B. C. D.
12.(2023 贵池区二模)如图,四边形为平行四边形,和平行于轴,点在函数上,点、在函数上,点在轴上,则四边形的面积为
A.13 B.18 C.21 D.26
13.(2023 新城区一模)如图,过反比例函数的图象上一点作轴于点,连接,若,则的值为 .
14.(2023春 靖江市期末)如图,在矩形中,,,是上的一个动点不与,重合),过点的反比例函数的图象与边交于点,若时,则 .
15.(2023秋 盐城月考)如图,点在双曲线的第一象限的图象上,垂直于轴于点,点在轴的正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则值为 .
五.反比例函数图象上点的坐标特征(共15小题)
16.(2023秋 霍邱县校级月考)若点在函数的图象上,则以下哪个点一定在这个函数的图象上
A. B. C. D.
17.(2023春 新乡期末)若,,,在反比例函数图象上,则下列各式正确的是
A. B. C. D.
18.(2023 建湖县三模)如图,在菱形中,,,点为原点,点在轴正半轴上,若函数的图象经过点,则的值是
A.24 B.12 C. D.
19.(2023春 辉县市期末)若点,,在反比例函数图象上,则下列结论正确的是
A. B. C. D.
20.(2023 楚雄市校级二模)如图,矩形在平面直角坐标系中,点,轴,且,,若反比例函数与矩形有交点,则的取值范围是
A. B. C. D.
21.(2022秋 武安市期末)已知反比例函数的图象在各自象限内,随的增大而增大,则下列各点可能在这个函数图象上的是
A. B. C. D.
22.(2023春 市中区期末)若点、、在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
23.(2023 遂溪县一模)若点,,,,,都在反比例函数的图象上,则,,的大小关系是
A. B. C. D.
24.(2023秋 庐阳区校级期中)已知点在反比例函数图象上,则点一定在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
25.(2023 襄阳)点,都在反比例函数的图象上,则 .(填“”或“”
26.(2023秋 蒙城县月考)如图,已知反比例函数,在第一象限的图象,过上任意一点,作轴的平行线交于点,交轴于点过点作轴的垂线交于点,交轴于点,连接,,则:
①的面积为 ;
② .
27.(2023秋 如皋市期中)在平面直角坐标系中,若点和点都在反比例函数的图象上,则 (填“”“ ”或“” .
28.(2023 香坊区校级开学)在反比例函数的图象上有两点,和,,若时,则 (填“”、“ ”、“ ” .
29.(2022秋 天心区期末)若点,,在反比例函数的图象上,则,,的大小关系是 .
30.(2023 巴东县模拟)如图,在平面直角坐标系中,为坐标原点,双曲线经过的顶点与斜边中点.
(1)求;
(2)若双曲线经过点,求.
六.待定系数法求反比例函数解析式(共1小题)
31.(2022秋 徐汇区期末)已知,与成正比例,与成反比例,且当时,;当时,.
(1)求关于的函数解析式;
(2)当时,求的值.
七.反比例函数与一次函数的交点问题(共13小题)
32.(2023 咸丰县一模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,连接,.
(1)求反比例函数的表达式;
(2)求的面积.
33.(2022秋 玉泉区校级期末)如图,一次函数的图象分别交轴、轴于,两点,交反比例函数图象于,两点.
(1)求直线的表达式;
(2)点是线段上一点,若,求点的坐标;
(3)请你根据图象直接写出不等式的解集.
34.(2023春 罗定市校级期中)如图所示,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集.
35.(2023秋 来宾期中)如图,直线与反比例函数的图象相交于点、,与轴交于点,其中点的坐标为,点的横坐标为.
(1)试确定反比例函数的表达式;
(2)求的坐标.
36.(2023春 长春期中)如图,正比例函数的图象与反比例函数的图象相交于、两点,点的横坐标为2,当时,的取值范围是
A.或 B.或
C.或 D.或
37.(2023春 安溪县期中)若直线与双曲线交于点,,,,则的值为
A.2023 B. C. D.
38.(2023秋 温江区校级期中)如图,直线交轴于点,交反比例函数于点,以为边的正方形的顶点在轴上,顶点在双曲线上,则的值为 .
39.(2023秋 泰山区期中)如图,直线与双曲线交于、两点,过点作轴,垂足为点,连接,若,则的值是 .
40.(2023 大东区模拟)如图,直线交轴于点,交反比例函数的图象于,两点,过点作轴,垂足为点,连接,若,则的值为 .
41.(2023秋 朝阳区校级期中)在平面直角坐标系中,记函数的图象为,直线经过,与图象交于,两点.
(1)求的值;
(2)横、纵坐标都是整数的点叫做整点.记图象在,之间的部分与线段围成的区域(不含边界)为.
①当时,区域内的整点个数为 个;
②各区域内恰有4个整点,结合函数图象,的取值范围为 .
42.(2023秋 兴宾区期中)如图,一次函数的图象与反比例函数的图象交于第一象限,两点,与坐标轴交于、两点,连接,是坐标原点).
(1)求反比例函数的表达式;
(2)求的面积;
43.(2023 泰山区校级自主招生)在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,过点作轴,垂足为,,,点的坐标为.
(1)求的周长和面积;
(2)求该反比例函数和一次函数的解析式.
44.(2023 肇源县开学)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
八.根据实际问题列反比例函数关系式(共1小题)
45.(2022秋 丛台区校级期末)验光师测的一组关于近视眼镜的度数与镜片的焦距的数据,如表:
(单位:度) 100 200 400 500
(单位:米) 1.00 0.50 0.25 0.20
则关于的函数关系式是 .
九.反比例函数的应用(共4小题)
46.(2023 淮阳区三模)如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示.
2 1 0.5 0.4
桌面所受压强 100 200 400 500 800
(1)根据表中数据,求桌面所受压强与受力面积之间的函数表达式及的值.
(2)现想将另一长、宽、高分别为,,,且与该长方体相同重量的长方体按如图2所示的方式(即面向上)放置于该水平玻璃桌面上.若该玻璃桌面能承受的最大压强为,请你判断这种摆放方式是否安全?并说明理由.若将此长方体面向下摆放,请直接判断是否安全.
47.(2022秋 南华县期末)元旦假期,李老师驾驶小汽车从甲地匀速行驶到乙地,当小汽车匀速行驶的速度为时,行驶时间为;设小汽车匀速行驶的速度为,行驶的时间为.
(1)求关于的函数表达式;
(2)若小汽车匀速行驶的速度为,则从乙地返回甲地需要几小时?
48.(2023秋 房山区期中)已知蓄电池两端电压为定值,电流与的函数关系为,当时,,则当时,的值为
A. B. C. D.
49.(2023 东阳市三模)
设计货船通过双曲线桥的方案
素材1 一座曲线桥如图1所示,当水面宽米时,桥洞顶部离水面距离米.已知桥洞形如双曲线,图2是其示意图,且该桥关于对称.
素材2 如图4,一艘货船露出水面部分的横截面为矩形,测得米,米.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度(米与货船增加的载重量(吨满足函数表达式.
问题解决
任务1 确定桥洞的形状 ①建立平面直角坐标系如图3所示,显然,落在第一象限的角平分线上. 甲说:点可以在第一象限角平分线的任意位置. 乙说:不对吧?当点落在,时,点的坐标为 ,此时过点的双曲线的函数表达式为 ,而点所在双曲线的函数表达式为显然不符合题意.
任务2 拟定方案 此时货船能通过该桥洞吗?若能,请说明理由;若不能,至少要增加多少吨货物?
一十.反比例函数综合题(共2小题)
50.(2023秋 金水区校级期中)如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内,两点在右侧),分别交轴,轴于,两点.
(1)求和的值;
(2)求点的坐标;
(3)在轴上是否存在一点,使以,,为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
51.(2023 青岛模拟)如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于、两点,过点作轴于点,,,点的坐标为
(1)求一次函数和反比例函数的表达式;
(2)是轴上一点,且是等腰三角形,请直接写出所有符合条件的点坐标.
第六章 反比例函数专项复习卷
参考答案与试题解析
一.反比例函数的定义(共4小题)
1.(2023 天山区校级开学)下列各式中、均不为,和成反比例的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义:为常数且,逐一判断即可解答.
【解答】解:、,
,
和成正比例,
故不符合题意;
、,
,
和成正比例,
故不符合题意;
、,
,
和成反比例,
故符合题意;
、,
,
和不成比例,
故不符合题意;
故选:.
2.(2022秋 九龙坡区期末)下列函数中,是的反比例函数的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义回答即可.
【解答】解:、该函数是正比例函数,故本选项不符合题意;
、该函数不是反比例函数,故本选项不符合题意;
、该函数是正比例函数,故本选项不符合题意;
、该函数是反比例函数,故本选项符合题意.
故选:.
3.(2023春 灌云县月考)已知与成反比例,且其函数图象经过点.
(1)求与的函数关系式;
(2)求当时,的值.
【答案】(1);
(2).
【分析】(1)由于与成反比例,设,代入,解得的值即可;
(2)将代入反比例函数解析式,解得的值即可.
【解答】解:(1)设与的函数关系式为,
又图象经过点,则,
与的函数关系式为.
故答案为:;
(2)将代入,得到,
当时,.
4.(2022秋 沂南县期末)下列函数关系式中属于反比例函数的是
A. B. C. D.
【答案】
【分析】根据反比例函数的定义逐项判断选项求解.
【解答】解:为正比例函数,选项不符合题意.
为一次函数,选项不符合题意.
为二次函数,选项不符合题意.
为反比例函数,选项符合题意.
故选:.
二.反比例函数的图象(共1小题)
5.(2023 平阴县一模)反比例函数与一次函数在同一坐标系中的大致图象可能是
A. B.
C. D.
【答案】
【分析】根据一次函数图象判定、的符号,根据的符号判定反比例函数图象所在的象限.
【解答】解:、一次函数的图象经过第一、三象限,则,与轴交于负半轴,则,所以,则反比例经过第二、四象限,不符合题意;
、一次函数的图象经过第二、四象限,则,与轴交于负半轴,则,所以,则反比例经过第一、三象限,不符合题意;
、一次函数的图象经过第二、四象限,则,与轴交于正半轴,则,所以,则反比例经过第二、四象限,不符合题意;
、一次函数的图象经过第一、三象限,则,与轴交于负半轴,则,所以,则反比例经过第二、四象限,符合题意;
故选:.
三.反比例函数的性质(共3小题)
6.(2022秋 海淀区校级期末)双曲线截直线,所得的线段长度为 .
【答案】.
【分析】解析式联立成方程组,解方程组求得交点坐标,进一步即可求得所截线段的长度.
【解答】解:由解得或,
双曲线与直线的交点为,,
所截得的线段的长度为:,
故答案为:.
7.(2023秋 安乡县月考)若的取值范围如图所示,则在反比例函数的图象的每一个分支上,随的增大而 增大 .
【答案】增大.
【分析】由图得,即,得,故反比例函数的图象在二四象限,故反比例函数的图象的每一个分支上,随的增大而增大.
【解答】解:由图得,即,
得,
故反比例函数的图象在二四象限,
故反比例函数的图象的每一个分支上,随的增大而增大.
故答案为:增大.
8.(2023春 灌云县期末)若反比例函数的图象在第一、三象限,则的取值范围是 .
【答案】.
【分析】根据反比例函数的图象在第一、第三象限列出关于的不等式,求出的取值范围即可.
【解答】解:反比例函数的图象在第一、第三象限,
,解得.
故答案为:.
四.反比例函数系数k的几何意义(共7小题)
9.(2023 河东区一模)如图,在平面直角坐标系中,点在第一象限,轴于点,函数的图象与线段交于点,且.若的面积为12,则的值为
A.4 B.6 C.8 D.12
【答案】
【分析】连接,如图,根据三角形面积公式,由得到,可计算出,再根据反比例函数比例系数的几何意义得到,然后去绝对值即可得到满足条件的的值.
【解答】解:连接,如图,
轴于点,,
,
,
,
而,
.
故选:.
10.(2023春 卧龙区期中)如图,若反比例函数的图象经过点,轴于点,且的面积3,则的值为
A. B. C.3 D.6
【答案】
【分析】根据反比例函数比例系数的几何意义即可解决问题.
【解答】解:连接,,
轴于点,
.
.
.
反比例函数的图象在第一、三象限,
.
.
故选:.
11.(2023 鼓楼区校级三模)如图,在轴的正半轴上依次截取,过点,,,分别作轴的垂线与反比例函数的图象相交于点,,,得△,△,△,并设其面积分别为,,,以此类推,则的值为
A. B. C. D.
【答案】
【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是个定值,,由反比例函数解析式中,得出△,△,△,,△的面积都为1,而为的,且△与△的高为同一条高,故△的面积为△的面积的,由△的面积都为1,得出△的面积,即为的值.
【解答】解:连接,,,,如图所示:
过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是个定值,,
,即,
又,
,
,,,,,
△与△的高为同一条高,
,
.
故选:.
12.(2023 贵池区二模)如图,四边形为平行四边形,和平行于轴,点在函数上,点、在函数上,点在轴上,则四边形的面积为
A.13 B.18 C.21 D.26
【答案】
【分析】作轴于,轴于,轴于,根据平行四边形的面积公式以及反比例函数系数的几何意义即可求得.
【解答】解:作轴于,轴于,轴于,
四边形为平行四边形,和平行于轴,
,,
.
故选:.
13.(2023 新城区一模)如图,过反比例函数的图象上一点作轴于点,连接,若,则的值为 .
【分析】先设出点的坐标,由的面积可求出的值,即,即可写出反比例函数的解析式.
【解答】解:设点坐标为,
由图可知点在第二象限,
,,
又轴,
,,
,
,
故答案为:.
14.(2023春 靖江市期末)如图,在矩形中,,,是上的一个动点不与,重合),过点的反比例函数的图象与边交于点,若时,则 4 .
【答案】4.
【分析】连接,利用同底面积比等于高之比,得到点坐标,再利用反比例函数的关系式的求法计算即可.
【解答】解:连接,
由题意得:三角形的面积,
,
,
,,
,
,
故答案为:4.
15.(2023秋 盐城月考)如图,点在双曲线的第一象限的图象上,垂直于轴于点,点在轴的正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则值为 4 .
【答案】4.
【分析】由,的面积为3,得到的面积为1,则的面积为4,设点坐标为,则,,,,利用得,整理可得,即可得到的值.
【解答】解:连,如图,
,的面积为3,
的面积为1,
的面积为4,
设点坐标为,则,,
而点为的中点,
,
,
,
,
把代入双曲线,
.
故答案为:4.
五.反比例函数图象上点的坐标特征(共15小题)
16.(2023秋 霍邱县校级月考)若点在函数的图象上,则以下哪个点一定在这个函数的图象上
A. B. C. D.
【答案】
【分析】先求出的值,再根据双曲线上的点的横纵坐标之积等于,进行判断即可.
【解答】解:点在函数的图象上,
,
,,,,
点一定在这个函数的图象上.
故选:.
17.(2023春 新乡期末)若,,,在反比例函数图象上,则下列各式正确的是
A. B. C. D.
【答案】
【分析】根据反比例函数的性质得出函数图象在第一、三象限,并且在每个象限内,随的增大而减小,再根据反比例函数的性质比较即可.
【解答】解:反比例函数数中,
函数图象在第一、三象限,并且在每个象限内,随的增大而减小,
点,,,在反比例函数图象上,,
,,
即,
故选:.
18.(2023 建湖县三模)如图,在菱形中,,,点为原点,点在轴正半轴上,若函数的图象经过点,则的值是
A.24 B.12 C. D.
【答案】
【分析】先根据菱形的性质求出点坐标,再把点坐标代入反比例函数的解析式即可得出的值.
【解答】解:在菱形中,,,
,
反比例函数的图象经过点,
.
故选:.
19.(2023春 辉县市期末)若点,,在反比例函数图象上,则下列结论正确的是
A. B. C. D.
【答案】
【分析】由题意可知函数的图象在一、三象限,由三点的横坐标可知点,在第三象限,在第一象限,根据反比例函数的增减性及各象限内点的坐标特点即可解答.
【解答】解:反比例函数中,,
此函数的图象在一、三象限,在每一象限内,随的增大而减小;
,,
点,在第三象限,在第一象限,
,,
,
故选:.
20.(2023 楚雄市校级二模)如图,矩形在平面直角坐标系中,点,轴,且,,若反比例函数与矩形有交点,则的取值范围是
A. B. C. D.
【答案】
【分析】根据矩形的性质求得点的坐标,把、的坐标分别代入求得的值,根据图象即可求解.
【解答】解:矩形的边,,点,
,
当反比例函数经过点时,则;
当反比例函数经过点时,则,
若反比例函数与矩形有交点,则的取值范围是:,
故选:.
21.(2022秋 武安市期末)已知反比例函数的图象在各自象限内,随的增大而增大,则下列各点可能在这个函数图象上的是
A. B. C. D.
【答案】
【分析】根据反比例函数的性质判断即可.
【解答】解:因为反比例函数的图象在各自象限内,随的增大而增大,
所以,
.,故本选项符合题意;
.,故本选项不符合题意;
.,故本选项不符合题意;
.,故本选项不符合题意;
故选:.
22.(2023春 市中区期末)若点、、在反比例函数的图象上,则、、的大小关系是
A. B. C. D.
【答案】
【分析】根据反比例函数图象上点的坐标特征求出、、的值,比较后即可得出结论.
【解答】解:点,,在反比例函数的图象上,
,,,
又,
.
故选:.
23.(2023 遂溪县一模)若点,,,,,都在反比例函数的图象上,则,,的大小关系是
A. B. C. D.
【答案】
【分析】直接把各点坐标代入反比例函数的解析式,求出,,的值,再比较大小即可.
【解答】解:点,,,,,都在反比例函数的图象上,
,解得;
,解得;
,解得,
,
.
故选:.
24.(2023秋 庐阳区校级期中)已知点在反比例函数图象上,则点一定在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【分析】把点代入反比例函数解析式,可得,可得点一定在第一象限.
【解答】解:点在反比例函数图象上,
,
,
点一定在第一象限.
故选:.
方法二:
反比例函数中,,
图象的两个分支在一、三象限,
点在反比例函数的图象上,
点一定在第一象限.
故选:.
25.(2023 襄阳)点,都在反比例函数的图象上,则 .(填“”或“”
【答案】.
【分析】根据反比例函数的第一象限图象上,随的增大而减小判断即可.
【解答】解:点,在反比例函数的第一象限图象上,随的增大而减小,
.
故答案为:.
26.(2023秋 蒙城县月考)如图,已知反比例函数,在第一象限的图象,过上任意一点,作轴的平行线交于点,交轴于点过点作轴的垂线交于点,交轴于点,连接,,则:
①的面积为 ;
② .
【答案】,.
【分析】设点的坐标为,则,,,,,由此即可得出,结合即可证出,再根据相似三角形的性质即可得出的值,再利用相似三角形的性质求出的面积.
【解答】解:设点的坐标为,
作轴的平行线交于,交轴于点,过点作轴的垂线交于,交轴于点,
,,,,,
,,,,
.
又,
,
.
,
,
.
故答案为:,.
27.(2023秋 如皋市期中)在平面直角坐标系中,若点和点都在反比例函数的图象上,则 (填“”“ ”或“” .
【答案】
【分析】根据函数的增减性先看两个点是否在同一个象限内,比较两个点横坐标的大小即可确定值的大小.
【解答】解:在反比例函数中,,
在每一象限内,随的增大而减小,
点,都在第一象限,,
.
故答案为:.
28.(2023 香坊区校级开学)在反比例函数的图象上有两点,和,,若时,则 (填“”、“ ”、“ ” .
【答案】.
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断出和的大小关系.
【解答】解:反比例函数,
该函数的图象位于第一、三象限,在每个象限内,随的增大而减小,第一象限内的都大于0,第三象限内的都小于0,
,
,
故答案为:.
29.(2022秋 天心区期末)若点,,在反比例函数的图象上,则,,的大小关系是 .
【答案】.
【分析】先由得到函数在第二象限和第四象限内的函数值随的增大而增大,然后得到,,的大小关系.
【解答】解:反比例系数,
函数在第二象限和第四象限内的函数值随的增大而增大,
,
,
故答案为:.
30.(2023 巴东县模拟)如图,在平面直角坐标系中,为坐标原点,双曲线经过的顶点与斜边中点.
(1)求;
(2)若双曲线经过点,求.
【答案】或.
【分析】(1)将点代入,即可得出的值;
(2)过点,,分别作轴的垂线,垂足分别为,,,先由点得,,证和相似得,据此可设,,则点的坐标为,再由中点坐标公式得点,然后将点代入列出关于的方程,解方程求出的值,继而得点的坐标,进而可求出的值.
【解答】解:(1)双曲线经过点,
.
(2)过点,分别作轴的垂线,垂足分别为,,
点,
,,
,
,
又,
,
,
,
,
可设,,
点的坐标为,
点为的中点,点,
由中点坐标公式得点的坐标为,
双曲线经过点,
,
解得:,,
点或,
双曲线经过点,
或.
六.待定系数法求反比例函数解析式(共1小题)
31.(2022秋 徐汇区期末)已知,与成正比例,与成反比例,且当时,;当时,.
(1)求关于的函数解析式;
(2)当时,求的值.
【答案】(1).
(2).
【分析】(1)根据正比例函数和反比例函数的定义设,,则,再把两组对应值代入得到关于、的方程组,然后解方程组求出、即可.
(2)把代入(1)中求得的解析式即可求得.
【解答】解:(1)设,,
则,
根据题意得,
解得.
所以与的函数表达式为.
(2)把代入得,.
七.反比例函数与一次函数的交点问题(共13小题)
32.(2023 咸丰县一模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,连接,.
(1)求反比例函数的表达式;
(2)求的面积.
【答案】(1);(2)60.
【分析】(1)把代入,从而可得答案;
(2)先求解两个函数的交点坐标,再求解一次函数与轴的交点坐标,再利用三角形的面积之差可得答案.
【解答】解:(1)把代入,
,
;
(2)由题意可得:,
,
整理得:,
解得:,,
方程组的解为:或,经检验符合题意;
,
如图,记与坐标轴的交点为,,
由可得:当可得,
,
.
33.(2022秋 玉泉区校级期末)如图,一次函数的图象分别交轴、轴于,两点,交反比例函数图象于,两点.
(1)求直线的表达式;
(2)点是线段上一点,若,求点的坐标;
(3)请你根据图象直接写出不等式的解集.
【答案】(1);(2);(3)②或.
【分析】(1)把点代入中,利用待定系数法求得反比例函数的解析式,进而求得的坐标,然后根据待定系数法即可求得直线的表达式;
(2)设点的坐标为,求得点的坐标为,得到,根据得出关的方程,解方程求得,从而求得点的坐标;
(3)根据图象即可求得.
【解答】(1)把点代入中,得:,
反比例函数的解析式为,
将点代入得,
设直线的表达式为,则有,
解得,
直线的表达式为;
(2)设点的坐标为,
点的坐标为,,
,
,
解得:,
点的坐标为;
(3)不等式的解集是,.
34.(2023春 罗定市校级期中)如图所示,已知,是一次函数的图象与反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集.
【答案】(1)反比例函数的表达式,一次函数的表达式;
(2)不等式的解集是或.
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)一次函数的值小于反比例函数的值的的取值范围,就是对应的一次函数的图象在反比例函数的图象的下边的自变量的取值范围.
【解答】解:(1)将点坐标代入反比例函数解析式中,得,
,
反比例函数的表达式,
将点代入得,
,
将、点代入中,得,
解得,
一次函数的表达式;
(2)不等式的解集是或.
35.(2023秋 来宾期中)如图,直线与反比例函数的图象相交于点、,与轴交于点,其中点的坐标为,点的横坐标为.
(1)试确定反比例函数的表达式;
(2)求的坐标.
【答案】(1)反比例函数的关系式为:;
(2).
【分析】(1)把点的坐标代入反比例函数中,可得的值,即可得出反比例函数的关系式;
(2)先利用待定系数法求一次函数的解析式,再令,可得点的坐标.
【解答】解:(1)点在反比例函数的图象上,
,
反比例函数的关系式为:;
(2)当时,,
,
把点和代入得:,
解得:,
,
当时,,
,
.
36.(2023春 长春期中)如图,正比例函数的图象与反比例函数的图象相交于、两点,点的横坐标为2,当时,的取值范围是
A.或 B.或
C.或 D.或
【答案】
【分析】由正、反比例的对称性结合点的横坐标即可得出点的横坐标,根据函数图象的上下位置关系结合交点的横坐标,即可得出不等式的解集.
【解答】解:正比例函数与反比例函数的图象均关于原点对称,点的横坐标为2,
点的横坐标为.
观察函数图象,发现:
当或时,正比例函数图象在反比例函数图象的上方,
当时,的取值范围是或.
故选:.
37.(2023春 安溪县期中)若直线与双曲线交于点,,,,则的值为
A.2023 B. C. D.
【答案】
【分析】根据反比例函数图象上点的坐标特征,两交点坐标关于原点对称,得到,,再代入得出答案.
【解答】解:由反比例函数图象上点的坐标特征可知点,,,关于原点对称,
,,
把,代入双曲线,得,
,
故选:.
38.(2023秋 温江区校级期中)如图,直线交轴于点,交反比例函数于点,以为边的正方形的顶点在轴上,顶点在双曲线上,则的值为 .
【答案】.
【分析】作轴于,轴于,先求得、的坐标,然后通过证得,得到,,即可求得,代入即可求得的值.
【解答】解:作轴于,轴于,
反比例函数过点,
,
,
,
,,
令,则,
,
,
,
四边形是正方形,
,,
,
,
,
,
,
,,
,
,
顶点在双曲线上,
,
故答案为:.
39.(2023秋 泰山区期中)如图,直线与双曲线交于、两点,过点作轴,垂足为点,连接,若,则的值是 .
【答案】.
【分析】先求出的面积,再根据反比例函数中的几何意义即可解决问题.
【解答】解:因为直线与双曲线交于、两点,
所以,两点关于坐标原点成中心对称,
即,
所以.
又因为,
所以.
所以,
解得.
又反比例函数图象位于第二、四象限,
所以,
所以.
故答案为:.
40.(2023 大东区模拟)如图,直线交轴于点,交反比例函数的图象于,两点,过点作轴,垂足为点,连接,若,则的值为 10 .
【答案】10.
【分析】根据反比例函数系数的几何意义即可求解.
【解答】解:连接,
轴,
,
轴,
,
,
,
,
解得:,
故答案为:10.
41.(2023秋 朝阳区校级期中)在平面直角坐标系中,记函数的图象为,直线经过,与图象交于,两点.
(1)求的值;
(2)横、纵坐标都是整数的点叫做整点.记图象在,之间的部分与线段围成的区域(不含边界)为.
①当时,区域内的整点个数为 6 个;
②各区域内恰有4个整点,结合函数图象,的取值范围为 .
【答案】(1)4;(2)①6;②.
【分析】(1)将点的坐标代入一次函数关系式可得答案;
(2)①结合图象分析可得答案;
②考虑临界位置,结合图象得出答案.
【解答】解:(1)直线经过点,
,
解得,
所以;
(2)①如图所示,区域内的整点有,,,,,,共6个.
故答案为:6;
②当时,区域内有4个整点,如图所示.
当时,区域内有4个整点,如图所示.
所以区域内有4个整点,的取值范围是.
故答案为:.
42.(2023秋 兴宾区期中)如图,一次函数的图象与反比例函数的图象交于第一象限,两点,与坐标轴交于、两点,连接,是坐标原点).
(1)求反比例函数的表达式;
(2)求的面积;
【答案】(1)为;(2)7.5.
【分析】(1)把代入求出,把代入求出即可;
(2)把,代入得出解析式,求出,,得出一次函数的解析式,把代入求出,得出,根据的面积代入求出即可.
【解答】解:(1)把代入,得,
反比例函数的表达式为:;
(2)把,代入得,
解得,,
一次函数的解析式为,
把代入,得,
,
.
43.(2023 泰山区校级自主招生)在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,过点作轴,垂足为,,,点的坐标为.
(1)求的周长和面积;
(2)求该反比例函数和一次函数的解析式.
【分析】(1)根据正切函数,可得的长,根据勾股定理,可得的长,根据三角形的周长和面积,可得答案;
(2)根据待定系数法,可得函数解析式.
【解答】解:(1)由,得
.即.
由勾股定理,得
,
的周长,
的面积;
(2)将点坐标代入得
,
反比例函数的解析式为;
当时,,解得,即.
将、点坐标代入,得,
解得,
一次函数的解析式为.
44.(2023 肇源县开学)如图在平面直角坐标系中,直线与反比例函数的图象交于、两点,与轴相交于点,已知点,的坐标分别为和.
(1)求反比例函数的解析式;
(2)请直接写出不等式的解集;
(3)点为反比例函数图象的任意一点,若,求点的坐标.
【答案】(1)反比例函数的解析式为;
(2)不等式的解集为或;
(3)点的坐标为或.
【分析】(1)先通过一次函数求出点坐标,利用待定系数法即可求出反比例函数解析式;
(2)求出点的坐标,根据图象求解即可;
(3)根据图象求出,再根据求出,即可求出.
【解答】解:(1)把点代入直线得:,
点的坐标为:,
反比例函数的图象过点,
,
即反比例函数的解析式为,
(2)由(1)得:点的坐标为:,
同理可求,点的坐标为:,
不等式的解集为或;
(3)把代入得:,
即点的坐标为:,
,
,
,
,
当点的纵坐标为3时,则,解得,
当点的纵坐标为时,则,解得,
点的坐标为或.
八.根据实际问题列反比例函数关系式(共1小题)
45.(2022秋 丛台区校级期末)验光师测的一组关于近视眼镜的度数与镜片的焦距的数据,如表:
(单位:度) 100 200 400 500
(单位:米) 1.00 0.50 0.25 0.20
则关于的函数关系式是 .
【分析】根据表格数据可得近视眼镜的度数与镜片的焦距成反比例,设关于的函数关系式是,再代入一对、的值可得的值,进而可得答案.
【解答】解:根据表格数据可得近视眼镜的度数与镜片的焦距成反比例,
设关于的函数关系式是,
,,
,
解得:,
关于的函数关系式是.
故答案为:.
九.反比例函数的应用(共4小题)
46.(2023 淮阳区三模)如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示.
2 1 0.5 0.4
桌面所受压强 100 200 400 500 800
(1)根据表中数据,求桌面所受压强与受力面积之间的函数表达式及的值.
(2)现想将另一长、宽、高分别为,,,且与该长方体相同重量的长方体按如图2所示的方式(即面向上)放置于该水平玻璃桌面上.若该玻璃桌面能承受的最大压强为,请你判断这种摆放方式是否安全?并说明理由.若将此长方体面向下摆放,请直接判断是否安全.
【答案】(1),;
(2)这种摆放方式安全,理由见解析.
【分析】(1)用待定系数法可得函数关系式;
(2)算出,即可求出,比较可得答案.
【解答】解:(1)由表格可知,压强与受力面积的乘积不变,故压强是受力面积的反比例函数,
设,将代入得:
,
解得,
桌面所受压强与受力面积之间的函数表达式为,
把代入得,;
(2)这种摆放方式安全,理由如下:
由图可知,
将长方体放置于该水平玻璃桌面上,,
,
这种摆放方式安全.
47.(2022秋 南华县期末)元旦假期,李老师驾驶小汽车从甲地匀速行驶到乙地,当小汽车匀速行驶的速度为时,行驶时间为;设小汽车匀速行驶的速度为,行驶的时间为.
(1)求关于的函数表达式;
(2)若小汽车匀速行驶的速度为,则从乙地返回甲地需要几小时?
【答案】(1);
(2)小汽车速度为时,从乙地到甲地需要.
【分析】(1)根据路程,速度,时间的关系,先求出从甲地到乙地路程,再列出函数关系式;
(2)结合(1),把代入求出的值即可.
【解答】解:(1)由题意可得从甲地到乙地路程为:,
与的关系式为:;
(2)当小汽车匀速行驶的速度为,即,
在中,令得,
解得,
答:小汽车速度为时,从乙地到甲地需要.
48.(2023秋 房山区期中)已知蓄电池两端电压为定值,电流与的函数关系为,当时,,则当时,的值为
A. B. C. D.
【答案】
【分析】先利用待定系数法求出函数解析式,再将的值代入求值即可.
【解答】解:电流与的函数关系为,当时,,
,
解得,
电流与的函数关系为,
当时,即,
解得.
故选:.
49.(2023 东阳市三模)
设计货船通过双曲线桥的方案
素材1 一座曲线桥如图1所示,当水面宽米时,桥洞顶部离水面距离米.已知桥洞形如双曲线,图2是其示意图,且该桥关于对称.
素材2 如图4,一艘货船露出水面部分的横截面为矩形,测得米,米.因水深足够,货船可以根据需要运载货物.据调查,船身下降的高度(米与货船增加的载重量(吨满足函数表达式.
问题解决
任务1 确定桥洞的形状 ①建立平面直角坐标系如图3所示,显然,落在第一象限的角平分线上. 甲说:点可以在第一象限角平分线的任意位置. 乙说:不对吧?当点落在,时,点的坐标为 , ,此时过点的双曲线的函数表达式为 ,而点所在双曲线的函数表达式为显然不符合题意.
任务2 拟定方案 此时货船能通过该桥洞吗?若能,请说明理由;若不能,至少要增加多少吨货物?
【答案】任务,,,乙正确;
任务2:此时货船不能通过该桥洞;要至少增加吨货物此货船能通过该桥洞.
【分析】任务1:设曲线的解析式为,把点,代入,可得曲线的解析式为,再由反比例函数图象的对称性可得:点是的中点,,过点、分别作轴、轴的平行线交于,过点作于,可得、是等腰直角三角形,进而可得,,,,点,在双曲线上与点在双曲线上矛盾;
任务2:设,,其中,则,,可得,由,,可得,,,可得,再根据矩形的性质可得,,即可判断此时货船不能通过;运用待定系数法可得直线的解析式为,进而可得直线与双曲线的交点,,即可求得答案.
【解答】解:任务1:设曲线的解析式为,把点,代入,得:,
解得:,
曲线的解析式为,
落在第一象限的角平分线上,
、关于对称,即、关于第一象限角平分线对称,
点是的中点,,
过点、分别作轴、轴的平行线交于,过点作于,如图,
则、是等腰直角三角形,
,
,
,,
,
,,
,,
,
点,在双曲线上,
点所在双曲线的函数表达式为显然不符合题意.
故答案为:,,,乙正确;
任务2:设,,其中,则,,如图,
点在直线上,
,即,
,,
,,,
,
,
,
,,,,,,,,
四边形是矩形,
,,
,,
,,,,
,
此时货船不能通过该桥洞;
设直线的解析式为,把,代入,得,
解得:,
直线的解析式为,
联立得,
解得:(舍去),,
,,
,即,
,
,
故要至少增加吨货物此货船能通过该桥洞.
答:此时货船不能通过该桥洞;要至少增加吨货物此货船能通过该桥洞.
一十.反比例函数综合题(共2小题)
50.(2023秋 金水区校级期中)如图,在平面直角坐标系中,一次函数与反比例函数交于第一象限内,两点在右侧),分别交轴,轴于,两点.
(1)求和的值;
(2)求点的坐标;
(3)在轴上是否存在一点,使以,,为顶点的三角形与相似?若存在,求出点的坐标.若不存在,请说明理由.
【答案】(1),;
(2);
(3)或.
【分析】(1)将点的坐标分别代入一次函数与反比例函数的解析式,解方程即可得出结论;
(2)由(1)知一次函数的解析式为,反比例函数的解析式为,联立可得点;
(3)由一次函数与轴,轴交于,两点,可得,;所以,;设,,,根据图形可知,需要分两种情况,①当时,,②当时,,分别求解可得出结论.
【解答】解:(1)一次函数与反比例函数交于点,
,,
,;
(2)由(1)知一次函数的解析式为,反比例函数的解析式为,
解得,,
;
(3)存在以,,为顶点的三角形与相似.
一次函数与轴,轴交于,两点,
,,
,,
设,
,,
①当时,,
,
,,
;
②当时,,
,
,,,
,
解得,
,
综上所述,或.
51.(2023 青岛模拟)如图,在平面直角坐标系中,一次函数与反比例函数的图象相交于、两点,过点作轴于点,,,点的坐标为
(1)求一次函数和反比例函数的表达式;
(2)是轴上一点,且是等腰三角形,请直接写出所有符合条件的点坐标.
【分析】(1)先根据勾股定理求出,,得出点,进而求出反比例函数解析式,再求出点坐标,最后用待定系数法求出直线解析式;
(2)设出点坐标,进而表示出,,,利用等腰三角形的两边相等建立方程求解即可得出结论.
【解答】解:(1)轴,
,
在中,,,
,,
,
,
又点在反比例函数上,
,
,
点,在直线上,
,
,
直线的表达式为;
(2)设点,
,,
,,,
是等腰三角形,
①当时,
,
,
或,
②当时,
,
(舍或,
,
③时,
,
,
,
即:当点坐标为,,或时,是等腰三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
