人教版八年级上册14.2.1 平方差公式 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级上册14.2.1 平方差公式 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 10:45:13 | ||
图片预览






文档简介
(共16张PPT)
§14.2.1 平方差公式
统编八年级上册第十四章14.2乘法公式
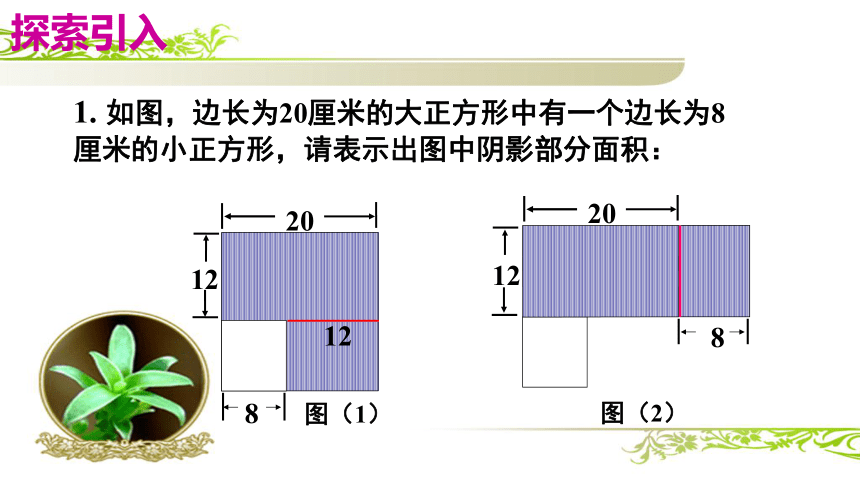
20
8
图(1)
探索引入
1. 如图,边长为20厘米的大正方形中有一个边长为8厘米的小正方形,请表示出图中阴影部分面积:
12
12
20
图(2)
8
12
探索引入
图(1)的面积为:
图(2)的面积为:
即:
从上式中你能发现一些有趣的现象吗?再举几个数试试.如果是一个数和一个字母,或两个都是字母呢?它们的情况又如何?
2. 计算下列各题:
(1) (x+2)(x-2) (2) (1+3a)(1-3a)
(3) (x+5y)(x-5y) (4) (y+3z)(y-3z)
观察以上算式及其计算结果,你发现了什么规律?能不能大胆猜测得出一个一般性的结论?
探索引入
你有什么发现?
(a+b)(a-b) =
猜想:
a2-b2
3.利用下列问题来猜想:
① 式子的左边具有什么共同特征?
②它们的结果有什么特征?
③能不能用字母表示你的发现?
探索引入
总结
平方差公式
两数的和乘以这两个数的差等于这两个数的平方差.
方法1
从代数角度:
(多项式与多项式相乘法则)
(合并同类项)
验证
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
a-b
a-b
方法2
从几何角度:
验证
(a+b)(a-b)=(a)2-(b)2
相反为b
相同为a
适当交换
合理加括号
(1)左边括号中的两项,
其中一项相同,
另一项则相反;
平方差公式的特征:
归纳
(2)右边则为“相同项”的平方减去“相反项”的平方。
平方差公式的特征:
归纳
归纳
平方差公式的特征:
(3)公式中的a和b可以是数,也可以是代数式.
归纳
平方差公式的特征:
(4)各因式项数相同.符号相同的项放在前面平方,符号相反的项放在后面平方.
随堂练习
1.下面各式的计算对不对?如果不对,应当怎样改正?
(2) ( 3a 2)(3a 2)=9a2 4
(1) (x+2)(x 2)=x2 2
解:(1)正确;
(2)错误,
( 3a 2)(3a 2)=4 9a2.
随堂练习
2.运用平方差公式计算:
解:( 5m n)(5m n)
=( n)2 (5m)2
=n2 25m2
(3) (2x+3)(2x 3) (3x+2)(2x 3)
(1) ( 5m n)(5m n)
解:
解:(2x+3)(2x 3) (3x+2)(2x 3)
=(2x)2 32 (6x2 9x+4x 6)
=4x2 9 6x2+9x 4x+6
= 2x2+5x 3
平方差公式的特征:
平方差公式:
平
方
差
公
式
两个数的和与这两个数的差的积,等于这两个数的平方差.
等号左边是两个二项式的积,且这两个二项式中有一项为相同项,另一项为相反项.
等号右边是相同项的平方减去相反项的平方.
公式中的字母可以表示具体的数,也可以表示单项式或多项式等式子.
(a+b)(a b)=a2 b2
§14.2.1 平方差公式
统编八年级上册第十四章14.2乘法公式
20
8
图(1)
探索引入
1. 如图,边长为20厘米的大正方形中有一个边长为8厘米的小正方形,请表示出图中阴影部分面积:
12
12
20
图(2)
8
12
探索引入
图(1)的面积为:
图(2)的面积为:
即:
从上式中你能发现一些有趣的现象吗?再举几个数试试.如果是一个数和一个字母,或两个都是字母呢?它们的情况又如何?
2. 计算下列各题:
(1) (x+2)(x-2) (2) (1+3a)(1-3a)
(3) (x+5y)(x-5y) (4) (y+3z)(y-3z)
观察以上算式及其计算结果,你发现了什么规律?能不能大胆猜测得出一个一般性的结论?
探索引入
你有什么发现?
(a+b)(a-b) =
猜想:
a2-b2
3.利用下列问题来猜想:
① 式子的左边具有什么共同特征?
②它们的结果有什么特征?
③能不能用字母表示你的发现?
探索引入
总结
平方差公式
两数的和乘以这两个数的差等于这两个数的平方差.
方法1
从代数角度:
(多项式与多项式相乘法则)
(合并同类项)
验证
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
a-b
a-b
方法2
从几何角度:
验证
(a+b)(a-b)=(a)2-(b)2
相反为b
相同为a
适当交换
合理加括号
(1)左边括号中的两项,
其中一项相同,
另一项则相反;
平方差公式的特征:
归纳
(2)右边则为“相同项”的平方减去“相反项”的平方。
平方差公式的特征:
归纳
归纳
平方差公式的特征:
(3)公式中的a和b可以是数,也可以是代数式.
归纳
平方差公式的特征:
(4)各因式项数相同.符号相同的项放在前面平方,符号相反的项放在后面平方.
随堂练习
1.下面各式的计算对不对?如果不对,应当怎样改正?
(2) ( 3a 2)(3a 2)=9a2 4
(1) (x+2)(x 2)=x2 2
解:(1)正确;
(2)错误,
( 3a 2)(3a 2)=4 9a2.
随堂练习
2.运用平方差公式计算:
解:( 5m n)(5m n)
=( n)2 (5m)2
=n2 25m2
(3) (2x+3)(2x 3) (3x+2)(2x 3)
(1) ( 5m n)(5m n)
解:
解:(2x+3)(2x 3) (3x+2)(2x 3)
=(2x)2 32 (6x2 9x+4x 6)
=4x2 9 6x2+9x 4x+6
= 2x2+5x 3
平方差公式的特征:
平方差公式:
平
方
差
公
式
两个数的和与这两个数的差的积,等于这两个数的平方差.
等号左边是两个二项式的积,且这两个二项式中有一项为相同项,另一项为相反项.
等号右边是相同项的平方减去相反项的平方.
公式中的字母可以表示具体的数,也可以表示单项式或多项式等式子.
(a+b)(a b)=a2 b2
