人教版八年级上册14.2.1 平方差公式 课件(共17张PPT)
文档属性
| 名称 | 人教版八年级上册14.2.1 平方差公式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 810.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 10:48:46 | ||
图片预览





文档简介
(共17张PPT)
平方差公式
算一算:看谁做的又快又准确!
(1)
(2)
(3)
(4)
观察思考:
①等式左边相乘的两个多项式有什么特点?
②等式右边的多项式有什么规律?
③你能归纳出上述等式的规律吗?
平方差公式
现在要对大家提出的猜想进行证明,我们将证明过程演示给大家.
证明:(a+b)(a-b)
我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.
符号语言: (a+b)(a-b)
文字语言:两数和与这两数差的积,等它们的平方差.
(多项式乘法法则)
(合并同类项)
议一议
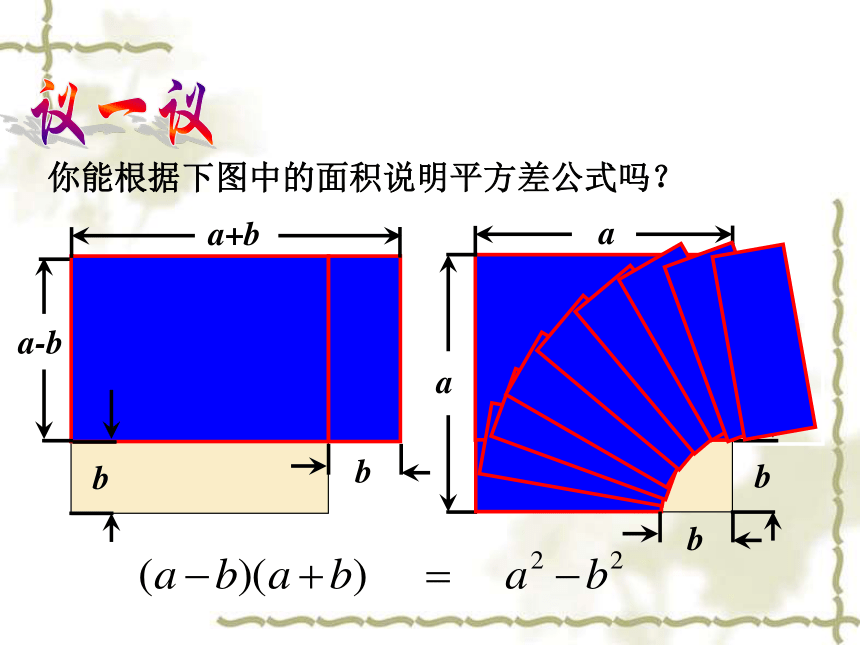
你能根据下图中的面积说明平方差公式吗?
a
a
b
b
a+b
a-b
b
b
平方差公式:
(a+b)(a b)=
a2 b2
两数和与这两数差的积,
等于
这两数的平方差.
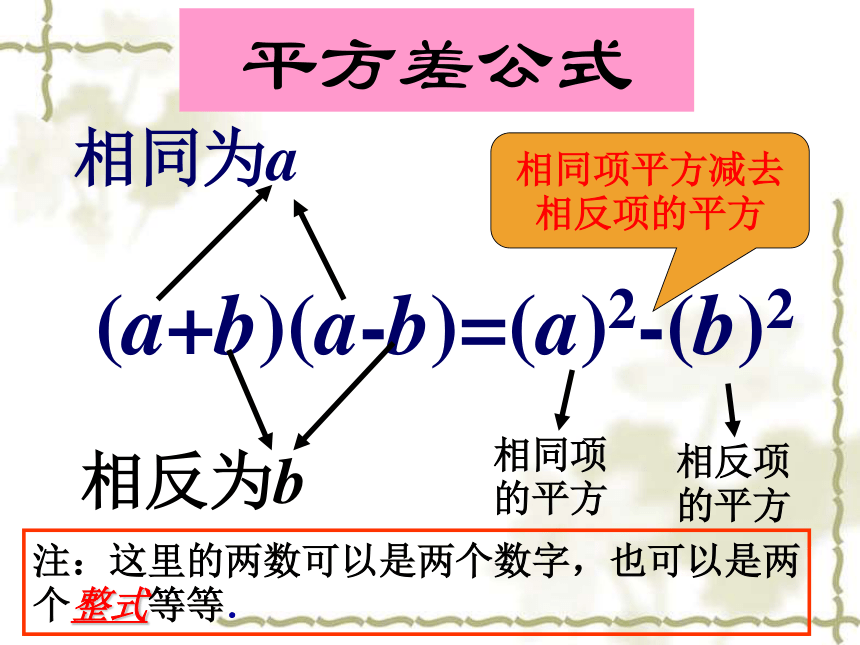
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
相同项的平方
相反项的平方
平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
相同项平方减去相反项的平方
例1 利用平方差公式计算:
(1)(5+6x)(5 6x);
(2)(x-2y)(x+2y);
(3)( m+n)( m n).
解:(1) (5+6x)(5 6x)=
(2)(x-2y) (x+2y) =
(3)( m+n)( m n )
52-(6x)2=
25-36x2
x2-(2y)2=
x2-4y2
=(-m)2-(n)2
=m2-n2
例2 利用平方差公式计算:
(1) (2)
解:(1)
(2)
运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b); (3) (-x+2y)(-x-2y).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
试试就能行
1.下面各式的计算对不对?如果不对,应当怎样改正?
( 1 ) (x+2)(x-2)=x2-2 ( )
( 2 ) (-a-b)(a-b)=-a2+b2 ( )
( 3 ) (3a-2)(-3a-2)=9a2-4 ( )
随堂练习
随堂练习
(1) (3a+2b)(3a-2b)
2、计算:
(2) (-x+1)(-x-1)
(3)(a+3b)(3b-a)
(1)103×97;
(1)103×97
=(100+3) ×(100-3 )
=1002 32
=9991.
例3、利用平方差公式计算:[]
解:
(2)118×122
(2)118×122
=(120 2) ×(120+2 )
=1202 22
=14396.
(1)
例4、计算:[]
解:(1)
(2)
(2)
(3m+2n)(3m-2n)
变式一 ( -3m+2n)(-3m-2n)
变式二 ( -3m-2n)(3m-2n)
变式三 (-3m-2n)(3m+2n)
= (-3m)2-(2n)2
变一变,你还能做吗?
利用平方差公式计算:
(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
拓展提升
小结
本节课你学到了什么
试用语言表述平方差公式 (a+b)(a b)= a2 b2.
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差.
变成公式标准形式后,再用公式.
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式.
要利用加法交换律,
对于不符合平方差公式标准形式者,
(a+b)(a-b)=(a)2-(b)2
相反为b
小结
相同为a
适当交换
合理加括号
平方差公式
平方差公式
算一算:看谁做的又快又准确!
(1)
(2)
(3)
(4)
观察思考:
①等式左边相乘的两个多项式有什么特点?
②等式右边的多项式有什么规律?
③你能归纳出上述等式的规律吗?
平方差公式
现在要对大家提出的猜想进行证明,我们将证明过程演示给大家.
证明:(a+b)(a-b)
我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.
符号语言: (a+b)(a-b)
文字语言:两数和与这两数差的积,等它们的平方差.
(多项式乘法法则)
(合并同类项)
议一议
你能根据下图中的面积说明平方差公式吗?
a
a
b
b
a+b
a-b
b
b
平方差公式:
(a+b)(a b)=
a2 b2
两数和与这两数差的积,
等于
这两数的平方差.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
相同项的平方
相反项的平方
平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
相同项平方减去相反项的平方
例1 利用平方差公式计算:
(1)(5+6x)(5 6x);
(2)(x-2y)(x+2y);
(3)( m+n)( m n).
解:(1) (5+6x)(5 6x)=
(2)(x-2y) (x+2y) =
(3)( m+n)( m n )
52-(6x)2=
25-36x2
x2-(2y)2=
x2-4y2
=(-m)2-(n)2
=m2-n2
例2 利用平方差公式计算:
(1) (2)
解:(1)
(2)
运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b); (3) (-x+2y)(-x-2y).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
试试就能行
1.下面各式的计算对不对?如果不对,应当怎样改正?
( 1 ) (x+2)(x-2)=x2-2 ( )
( 2 ) (-a-b)(a-b)=-a2+b2 ( )
( 3 ) (3a-2)(-3a-2)=9a2-4 ( )
随堂练习
随堂练习
(1) (3a+2b)(3a-2b)
2、计算:
(2) (-x+1)(-x-1)
(3)(a+3b)(3b-a)
(1)103×97;
(1)103×97
=(100+3) ×(100-3 )
=1002 32
=9991.
例3、利用平方差公式计算:[]
解:
(2)118×122
(2)118×122
=(120 2) ×(120+2 )
=1202 22
=14396.
(1)
例4、计算:[]
解:(1)
(2)
(2)
(3m+2n)(3m-2n)
变式一 ( -3m+2n)(-3m-2n)
变式二 ( -3m-2n)(3m-2n)
变式三 (-3m-2n)(3m+2n)
= (-3m)2-(2n)2
变一变,你还能做吗?
利用平方差公式计算:
(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
拓展提升
小结
本节课你学到了什么
试用语言表述平方差公式 (a+b)(a b)= a2 b2.
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差.
变成公式标准形式后,再用公式.
运用平方差公式时,要紧扣公式的特征,
找出相等的“项”和符号相反的“项”,然后应用公式.
要利用加法交换律,
对于不符合平方差公式标准形式者,
(a+b)(a-b)=(a)2-(b)2
相反为b
小结
相同为a
适当交换
合理加括号
平方差公式
