北师大版七年级下册1.5 平方差公式 课件(共21张PPT)
文档属性
| 名称 | 北师大版七年级下册1.5 平方差公式 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 00:00:00 | ||
图片预览




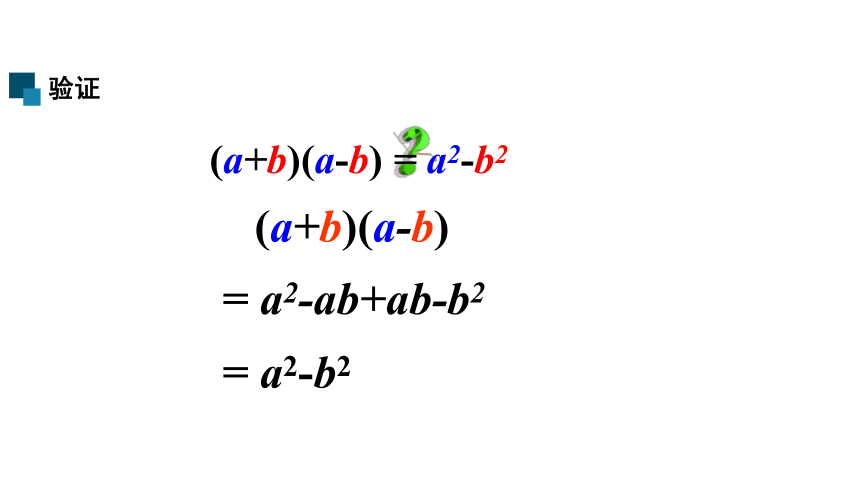



文档简介
(共21张PPT)
1.5 平方差公式
北师大版数学七年级下期
学习目标
1.经历平方差公式的探索与推导过程,掌握平方差公式的结构特征;
2.理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算;
3.通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.(新课标要求)
问题探究
一年忙到头, 灰太狼最终一只羊也没有吃到, 他决定把自家的土地租赁给羊们赚钱.
第一年, 把一块边长为a米的正方形土地租给慢羊羊种草.
第二年, 他对慢羊羊说: “我把这块地的一边增加5米, 另一边减少5米, 再继续租给你, 你也没吃亏, 你看如何 ”慢羊羊也觉得不吃亏, 就答应了. 回到羊村, 就把这件事对喜羊羊他们讲了, 大家一听, 都说道: “村长,您吃亏了!” 慢羊羊村长很吃惊……!
同学们, 你能告诉慢羊羊这是为什么吗
a米
a米
问题探究
5米
(a-5)米
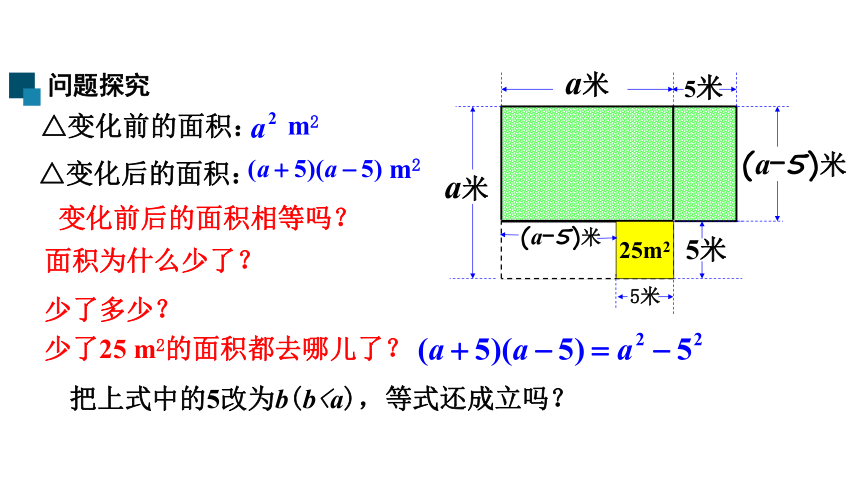
△变化前的面积:
△变化后的面积:
25m2
变化前后的面积相等吗?
面积为什么少了?
少了多少?
少了25 m2的面积都去哪儿了?
m2
m2
把上式中的5改为b(b5米
5米
(a-5)米
(a+b)(a-b) =
猜想
a2-b2
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
= a2-b2
验证
(a+b)(a-b)=a2-b2
观察:
1.等式左边的两个多项式有什么特点?
2.等式右边的多项式有什么规律?
3.请用一句话归纳总结出等式的规律.
平方差公式
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.
这是两个特殊的多项式相乘!
平方差公式
(a+b)(a-b)=a2-b2
相同项
符号相反项
(相同项)2-(符号相反项)2
用公式关键是识别两项:
完全相同项 — a
符号相反项 — b和-b
a,b可表示任意整式.
平方差公式
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
小试身手
(m3+n2)(m3-n2)
m3
n2
(m3)2-(n2)2
思考:
(a+b)( a b) 能用平方差公式计算吗?
判断: 下列能用平方差公式的有哪些?
口答下列各题:
(l)(-a+b)(a+b)=_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
继续努力
小试牛刀,活学活用
b2-a2
a2-b2
a2-b2
b2-a2
⑴ (5+6x)(5-6x)
a
a
b
b
(
+
)
(
-
)
= a2 - b2
=
52
你知道吗?
- (6x)2
先明确哪个是 a ,
哪个是 b.再动笔
例1 利用平方差公式计算:
= 25- 36x2
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y);
(4)(a-2)(a+2)(a2 + 4).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
试试就能行
巩固提高:运用平方差公式计算:
(4)(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
巩固提高:运用平方差公式计算:
☆ 问题:
你认为在运用平方差公式的过程应注意什么细节问题才能避免出错?
巩固提高:人人争当出题小专家:
请同学们自己编写3道利用平方差公式计算的题目,同桌两名同学互换做一做,做完之后再换过来互相检查一下。(时间:2分钟)
a
b
如图,在边长为a的大正方形中剪掉一个边长为b的小正方形.
(1)请表示剩余部分的面积.
(2)小颖将剩余部分拼成了一个长方形,这个长方形的长和宽分别是多少?你能表示出它的面积吗?
(3)这个过程可验证一个乘法公式的成立,这个乘法公式是什么?
数形结合,拓展延伸
(a+b)(a-b)=a2-b2
平方差公式
平面几何图形
拼图验证
以形助数,数形结合
数形结合百般好,隔离分家万事休.
◇思考:按照下面方法拼图可以验证哪些乘法公式?
数形结合,拓展延伸
本节课你有哪些收获?
小结
(a+b)(a-b)=a2-b2
相同项
符号相反项
(相同项)2-(符号相反项)2
平方差公式
(a,b可表示任意整式.)
平方差公式
平面几何图形
拼图验证
以形助数,数形结合
总结
完成
目标一
完成
目标二
完成
目标三
1.若(x-ay)(x+ay)=x2-16y2,则a=_______.
2.已知x2-y2=8,x-y=4,求x+y的值.
拓展延伸
1.5 平方差公式
北师大版数学七年级下期
学习目标
1.经历平方差公式的探索与推导过程,掌握平方差公式的结构特征;
2.理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算;
3.通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.(新课标要求)
问题探究
一年忙到头, 灰太狼最终一只羊也没有吃到, 他决定把自家的土地租赁给羊们赚钱.
第一年, 把一块边长为a米的正方形土地租给慢羊羊种草.
第二年, 他对慢羊羊说: “我把这块地的一边增加5米, 另一边减少5米, 再继续租给你, 你也没吃亏, 你看如何 ”慢羊羊也觉得不吃亏, 就答应了. 回到羊村, 就把这件事对喜羊羊他们讲了, 大家一听, 都说道: “村长,您吃亏了!” 慢羊羊村长很吃惊……!
同学们, 你能告诉慢羊羊这是为什么吗
a米
a米
问题探究
5米
(a-5)米
△变化前的面积:
△变化后的面积:
25m2
变化前后的面积相等吗?
面积为什么少了?
少了多少?
少了25 m2的面积都去哪儿了?
m2
m2
把上式中的5改为b(b
5米
(a-5)米
(a+b)(a-b) =
猜想
a2-b2
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
= a2-b2
验证
(a+b)(a-b)=a2-b2
观察:
1.等式左边的两个多项式有什么特点?
2.等式右边的多项式有什么规律?
3.请用一句话归纳总结出等式的规律.
平方差公式
(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.
这是两个特殊的多项式相乘!
平方差公式
(a+b)(a-b)=a2-b2
相同项
符号相反项
(相同项)2-(符号相反项)2
用公式关键是识别两项:
完全相同项 — a
符号相反项 — b和-b
a,b可表示任意整式.
平方差公式
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
小试身手
(m3+n2)(m3-n2)
m3
n2
(m3)2-(n2)2
思考:
(a+b)( a b) 能用平方差公式计算吗?
判断: 下列能用平方差公式的有哪些?
口答下列各题:
(l)(-a+b)(a+b)=_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
继续努力
小试牛刀,活学活用
b2-a2
a2-b2
a2-b2
b2-a2
⑴ (5+6x)(5-6x)
a
a
b
b
(
+
)
(
-
)
= a2 - b2
=
52
你知道吗?
- (6x)2
先明确哪个是 a ,
哪个是 b.再动笔
例1 利用平方差公式计算:
= 25- 36x2
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y);
(4)(a-2)(a+2)(a2 + 4).
解:(1)(3x+2)(3x-2)
=(3x)2-22
=9x2-4;
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
(3) (-x+2y)(-x-2y)
=(-x)2-(2y)2
= x2-4y2
试试就能行
巩固提高:运用平方差公式计算:
(4)(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
巩固提高:运用平方差公式计算:
☆ 问题:
你认为在运用平方差公式的过程应注意什么细节问题才能避免出错?
巩固提高:人人争当出题小专家:
请同学们自己编写3道利用平方差公式计算的题目,同桌两名同学互换做一做,做完之后再换过来互相检查一下。(时间:2分钟)
a
b
如图,在边长为a的大正方形中剪掉一个边长为b的小正方形.
(1)请表示剩余部分的面积.
(2)小颖将剩余部分拼成了一个长方形,这个长方形的长和宽分别是多少?你能表示出它的面积吗?
(3)这个过程可验证一个乘法公式的成立,这个乘法公式是什么?
数形结合,拓展延伸
(a+b)(a-b)=a2-b2
平方差公式
平面几何图形
拼图验证
以形助数,数形结合
数形结合百般好,隔离分家万事休.
◇思考:按照下面方法拼图可以验证哪些乘法公式?
数形结合,拓展延伸
本节课你有哪些收获?
小结
(a+b)(a-b)=a2-b2
相同项
符号相反项
(相同项)2-(符号相反项)2
平方差公式
(a,b可表示任意整式.)
平方差公式
平面几何图形
拼图验证
以形助数,数形结合
总结
完成
目标一
完成
目标二
完成
目标三
1.若(x-ay)(x+ay)=x2-16y2,则a=_______.
2.已知x2-y2=8,x-y=4,求x+y的值.
拓展延伸
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
