北师大版七年级下册1.5 平方差公式 教学设计(表格式)
文档属性
| 名称 | 北师大版七年级下册1.5 平方差公式 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 271.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-18 11:10:16 | ||
图片预览

文档简介
1.5 平方差公式 教学设计
版本 北师大版 学科 初中数学 年级 七年级下册第一章
章节 整式的乘除 课题 平方差公式
学习目标
1. 经历平方差公式的探索及推导过程,掌握平方差公式的结构特征; 2. 理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算; 3. 通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.
教学重难点
教学重点: 理解平方差公式的结构特征及几何意义,并能灵活运用平方差公式. 教学难点: 理解平方差公式的本质,即结构的不变性,字母的可变性,准确运用公式.
教学过程
教学环节 教师行为 学生活动 设计意图
第一环节:激趣导入问题探究 为了落实劳动教育,某班主任先把清洁区分成一块块边长为a米的正方形,然后再平均分给每一个值日组的同学. 下面有两位值日组同学的对话是这样的...... 教师引导学生回答: 变化前的面积:a2平方米; 变化后的面积:(a+5)(a-5)平方米; 变化前后的面积相等吗? 减掉的面积:5a平方米; 补上的面积:5(a-5)=(5a-52)平方米; 少了25平方米的面积都去哪儿了? (a+5)(a-5)= a2-52 把上式中的5改为b(b<a),等式还成立吗? 学生们大胆提出猜想: (a+b)(a-b)= a2-b2教师提问:牛顿曾说没有猜想就没有伟大的发现,有了猜想,那么猜想就一定正确吗?接下来请同学们利用前面学过的多项式与多项式相乘的运算法则验证(a+b)(a-b)是否等于 a2-b2. 学生在教师的引导下,思考,回答,大胆提出猜想: (a+b)(a-b)= a2-b2. 打扫校园卫生是学生们熟悉的场景,通过两个值日组同学换清洁区的情景,激趣导入,在此故事背景下学生们大胆提出猜想: (a+b)(a-b)= a2-b2,初步认识平方差公式.
第二环节:动手实践,收获新知 通过多项式乘多项式的运算法则推导出平方差公式(a+b)(a-b)= a2-b2. 引导学生观察平方差公式并回答以下问题: 等式左边的两个多项式有什么特点? 等式右边的多项式有什么规律? 请用一句话归纳总结出等式的规律. 平方差公式的左边是两数的和乘以这两数的差,右边正好等于这两数的平方差,左边的两个多项式中包含相同项a和符号相反项b,右边等于相同项的平方减去符号相反项的平方. 教师追问1: 应用平方差公式的关键是什么? 应用平方差公式的关键是: (1)找准相同项和符号相反项; (2)相同项的平方写在前面. 教师追问2: 平方差公式中的a,b只可以表示数吗? b可代表任意一个整式. 教师追问3: 平方差公式的本质是我们学过的多项式乘多项式的运算,我们已经学习了多项式乘以多项式的运算法则,为什么要用平方差公式进行整式的乘法运算? 平方差公式是整式乘法中的特殊情况,利用平方差公式计算比利用多项式乘法法则计算要简便易行.可以跳过法则直接写出结果. 学生们通过多项式乘多项式的运算法则推导出平方差公式(a+b)(a-b)= a2-b2. 学生在教师的提问与引导下归纳总结平方差公式的结构特点,理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 学生在教师的提问与引导下理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 理解平方差公式是整式乘法中的特殊情况,利用平方差公式计算比利用多项式乘法法则计算要简便易行.可以跳过法则直接写出结果.
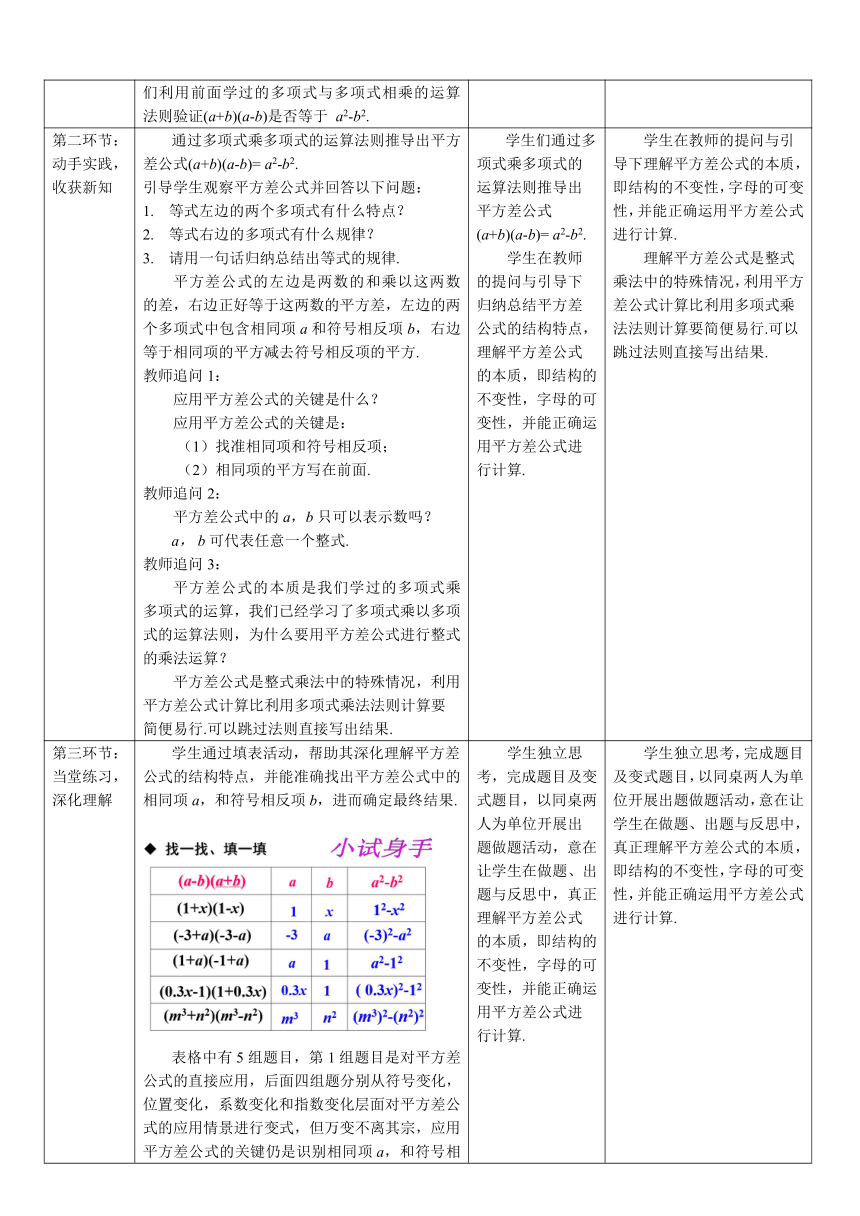
第三环节:当堂练习,深化理解 学生通过填表活动,帮助其深化理解平方差公式的结构特点,并能准确找出平方差公式中的相同项a,和符号相反项b,进而确定最终结果. 表格中有5组题目,第1组题目是对平方差公式的直接应用,后面四组题分别从符号变化,位置变化,系数变化和指数变化层面对平方差公式的应用情景进行变式,但万变不离其宗,应用平方差公式的关键仍是识别相同项a,和符号相反项b,并用相同项的平方减去相反项的平方. 教师追问4: (a+b)(-a-b)能用平方差公式计算吗? (a+b)(-a-b)不能利用平方差公式,因为其不具备平方差公式的结构特点,只有符号相反项,没有相同项,因为应用平方差公式前首先要识别其是否具备平方差公式的结构特点,具备才可以用,不具备只能按照多项式乘多项式的运算法则进行运算. 接下来学生通过做下面一组判断题,进一步深化对平方差公式结构特征的理解.通过板书,展示应用平方差公式计算时的过程步骤. 问题2: 结合刚刚我们做的题目,你认为在运用平方差公式的过程中应注意什么细节问题才能避免出错? 老师引导学生总结做题过程中的的易错点,培养学生归纳总结反思的能力,提高学生的学习主动性和成就感. 人人争当出题小专家: 问题1: 请同学们自己编写3道利用平方差公式计算的题目,同桌两名同学互换做一做,做完之后再换过来互相检查一下.(时间:3分钟) 教师展示部分学生出的题目,在学生所出题目的基础上,将平方差公式应用的变式情况补充完整,并让学生完成计算. 学生独立思考,完成题目及变式题目,以同桌两人为单位开展出题做题活动,意在让学生在做题、出题与反思中,真正理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 学生独立思考,完成题目及变式题目,以同桌两人为单位开展出题做题活动,意在让学生在做题、出题与反思中,真正理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算.
第四环节:知识补充,应用拓展 通过几何图形的剪切与拼接揭示平方差公式,了解平方差公式的几何背景,进而感受数形结合思想. 通过几何图形的剪切与拼接的动态展示从几何图形角度认识平方差公式,了解平方差公式的几何背景,进而感受数形结合思想. 通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.
第五环节:总结反思,提炼升华 本节课你收获了什么?有什么感悟? 学生思考,总结,回答本节课的所思所悟. 培养学生的总结和表达能力.
板书设计
版本 北师大版 学科 初中数学 年级 七年级下册第一章
章节 整式的乘除 课题 平方差公式
学习目标
1. 经历平方差公式的探索及推导过程,掌握平方差公式的结构特征; 2. 理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算; 3. 通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.
教学重难点
教学重点: 理解平方差公式的结构特征及几何意义,并能灵活运用平方差公式. 教学难点: 理解平方差公式的本质,即结构的不变性,字母的可变性,准确运用公式.
教学过程
教学环节 教师行为 学生活动 设计意图
第一环节:激趣导入问题探究 为了落实劳动教育,某班主任先把清洁区分成一块块边长为a米的正方形,然后再平均分给每一个值日组的同学. 下面有两位值日组同学的对话是这样的...... 教师引导学生回答: 变化前的面积:a2平方米; 变化后的面积:(a+5)(a-5)平方米; 变化前后的面积相等吗? 减掉的面积:5a平方米; 补上的面积:5(a-5)=(5a-52)平方米; 少了25平方米的面积都去哪儿了? (a+5)(a-5)= a2-52 把上式中的5改为b(b<a),等式还成立吗? 学生们大胆提出猜想: (a+b)(a-b)= a2-b2教师提问:牛顿曾说没有猜想就没有伟大的发现,有了猜想,那么猜想就一定正确吗?接下来请同学们利用前面学过的多项式与多项式相乘的运算法则验证(a+b)(a-b)是否等于 a2-b2. 学生在教师的引导下,思考,回答,大胆提出猜想: (a+b)(a-b)= a2-b2. 打扫校园卫生是学生们熟悉的场景,通过两个值日组同学换清洁区的情景,激趣导入,在此故事背景下学生们大胆提出猜想: (a+b)(a-b)= a2-b2,初步认识平方差公式.
第二环节:动手实践,收获新知 通过多项式乘多项式的运算法则推导出平方差公式(a+b)(a-b)= a2-b2. 引导学生观察平方差公式并回答以下问题: 等式左边的两个多项式有什么特点? 等式右边的多项式有什么规律? 请用一句话归纳总结出等式的规律. 平方差公式的左边是两数的和乘以这两数的差,右边正好等于这两数的平方差,左边的两个多项式中包含相同项a和符号相反项b,右边等于相同项的平方减去符号相反项的平方. 教师追问1: 应用平方差公式的关键是什么? 应用平方差公式的关键是: (1)找准相同项和符号相反项; (2)相同项的平方写在前面. 教师追问2: 平方差公式中的a,b只可以表示数吗? b可代表任意一个整式. 教师追问3: 平方差公式的本质是我们学过的多项式乘多项式的运算,我们已经学习了多项式乘以多项式的运算法则,为什么要用平方差公式进行整式的乘法运算? 平方差公式是整式乘法中的特殊情况,利用平方差公式计算比利用多项式乘法法则计算要简便易行.可以跳过法则直接写出结果. 学生们通过多项式乘多项式的运算法则推导出平方差公式(a+b)(a-b)= a2-b2. 学生在教师的提问与引导下归纳总结平方差公式的结构特点,理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 学生在教师的提问与引导下理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 理解平方差公式是整式乘法中的特殊情况,利用平方差公式计算比利用多项式乘法法则计算要简便易行.可以跳过法则直接写出结果.
第三环节:当堂练习,深化理解 学生通过填表活动,帮助其深化理解平方差公式的结构特点,并能准确找出平方差公式中的相同项a,和符号相反项b,进而确定最终结果. 表格中有5组题目,第1组题目是对平方差公式的直接应用,后面四组题分别从符号变化,位置变化,系数变化和指数变化层面对平方差公式的应用情景进行变式,但万变不离其宗,应用平方差公式的关键仍是识别相同项a,和符号相反项b,并用相同项的平方减去相反项的平方. 教师追问4: (a+b)(-a-b)能用平方差公式计算吗? (a+b)(-a-b)不能利用平方差公式,因为其不具备平方差公式的结构特点,只有符号相反项,没有相同项,因为应用平方差公式前首先要识别其是否具备平方差公式的结构特点,具备才可以用,不具备只能按照多项式乘多项式的运算法则进行运算. 接下来学生通过做下面一组判断题,进一步深化对平方差公式结构特征的理解.通过板书,展示应用平方差公式计算时的过程步骤. 问题2: 结合刚刚我们做的题目,你认为在运用平方差公式的过程中应注意什么细节问题才能避免出错? 老师引导学生总结做题过程中的的易错点,培养学生归纳总结反思的能力,提高学生的学习主动性和成就感. 人人争当出题小专家: 问题1: 请同学们自己编写3道利用平方差公式计算的题目,同桌两名同学互换做一做,做完之后再换过来互相检查一下.(时间:3分钟) 教师展示部分学生出的题目,在学生所出题目的基础上,将平方差公式应用的变式情况补充完整,并让学生完成计算. 学生独立思考,完成题目及变式题目,以同桌两人为单位开展出题做题活动,意在让学生在做题、出题与反思中,真正理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算. 学生独立思考,完成题目及变式题目,以同桌两人为单位开展出题做题活动,意在让学生在做题、出题与反思中,真正理解平方差公式的本质,即结构的不变性,字母的可变性,并能正确运用平方差公式进行计算.
第四环节:知识补充,应用拓展 通过几何图形的剪切与拼接揭示平方差公式,了解平方差公式的几何背景,进而感受数形结合思想. 通过几何图形的剪切与拼接的动态展示从几何图形角度认识平方差公式,了解平方差公式的几何背景,进而感受数形结合思想. 通过几何图形的面积来验证平方差公式,了解平方差公式的几何背景,进而感受数形结合思想,发展几何直观.
第五环节:总结反思,提炼升华 本节课你收获了什么?有什么感悟? 学生思考,总结,回答本节课的所思所悟. 培养学生的总结和表达能力.
板书设计
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
